計算幾何
計算幾何
處理幾何問題的演算法
一些會用到的工具
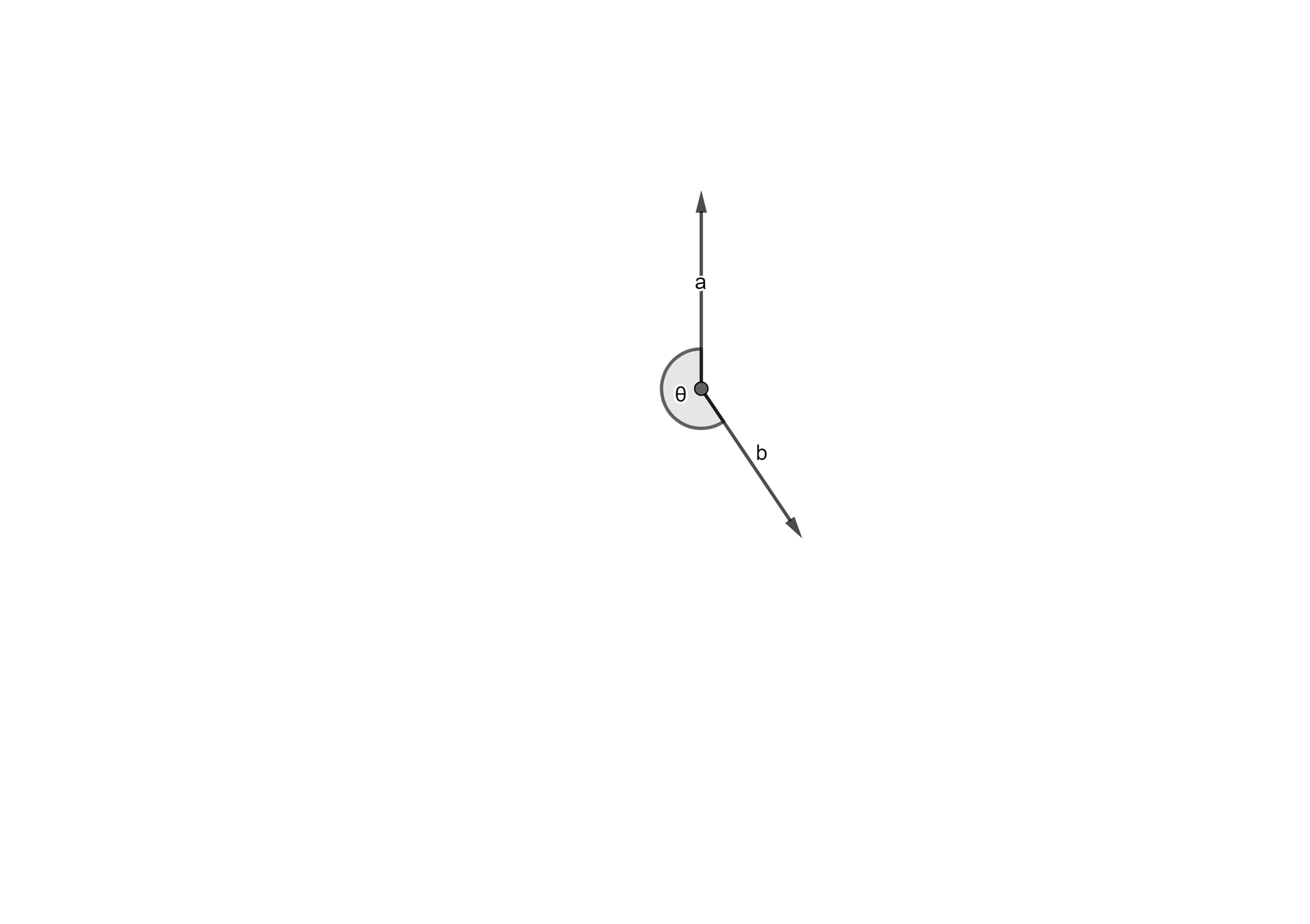
向量
具有方向性的數值
\(A = (1, 2), B = (3, 1), \overrightarrow{AB} = (2, -1)\)
向量有加法減法運算
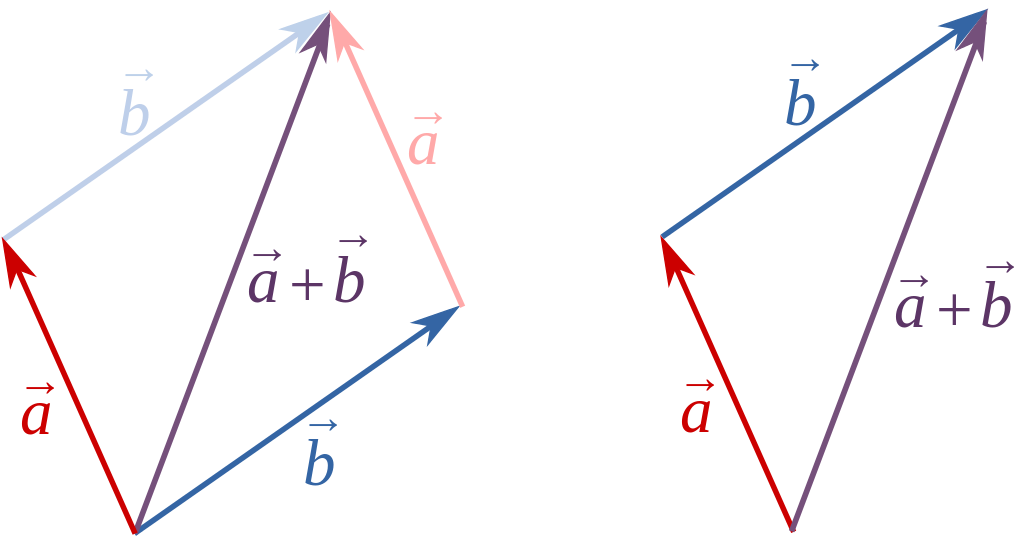
減法
加法
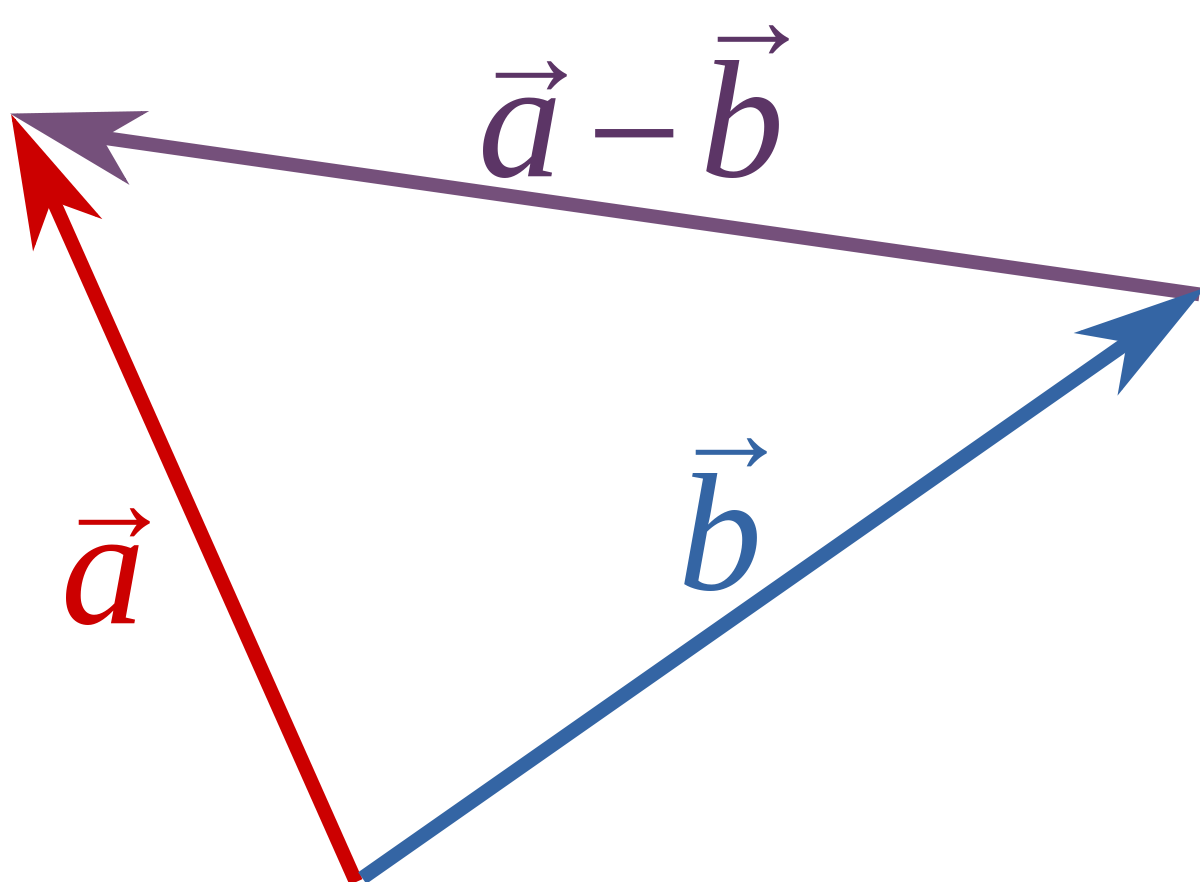
向量的長度記作\(|\vec v|\)
內積
\(\vec a 和 \vec b的內積記作\vec a \cdot \vec b\)
\(\vec a\cdot\vec b = |\vec a||\vec b|\cos\theta\)
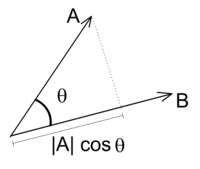
內積的計算
\(\vec a = (x_a, y_a)\)
\(\vec b = (x_b, y_b)\)
\(x_a \quad\quad y_a\)
\(x_b \quad\quad y_b\)
內積的計算
\(\vec a = (x_a, y_a)\)
\(\vec b = (x_b, y_b)\)
\(x_a \quad\quad y_a\)
\(x_b \quad\quad y_b\)
\(\vec a \cdot \vec b = x_a x_b + y_a y_b\)
內積的用處
用於判斷兩向量是否垂直
\(\vec a \cdot \vec b = |\vec a||\vec b|\cos\theta\)
如果\(\theta = 90\degree\)
\(cos \theta = 0\)
\(\vec a \cdot \vec b = 0\)
平面外積(行列式)
\(\begin{vmatrix}x_a & x_b \\y_a & y_b\end{vmatrix} = |\vec a||\vec b|\sin\theta\)
這邊用行列式的方式來表示
計算方式
\(\begin{vmatrix}x_a & x_b \\y_a & y_b\end{vmatrix}\)
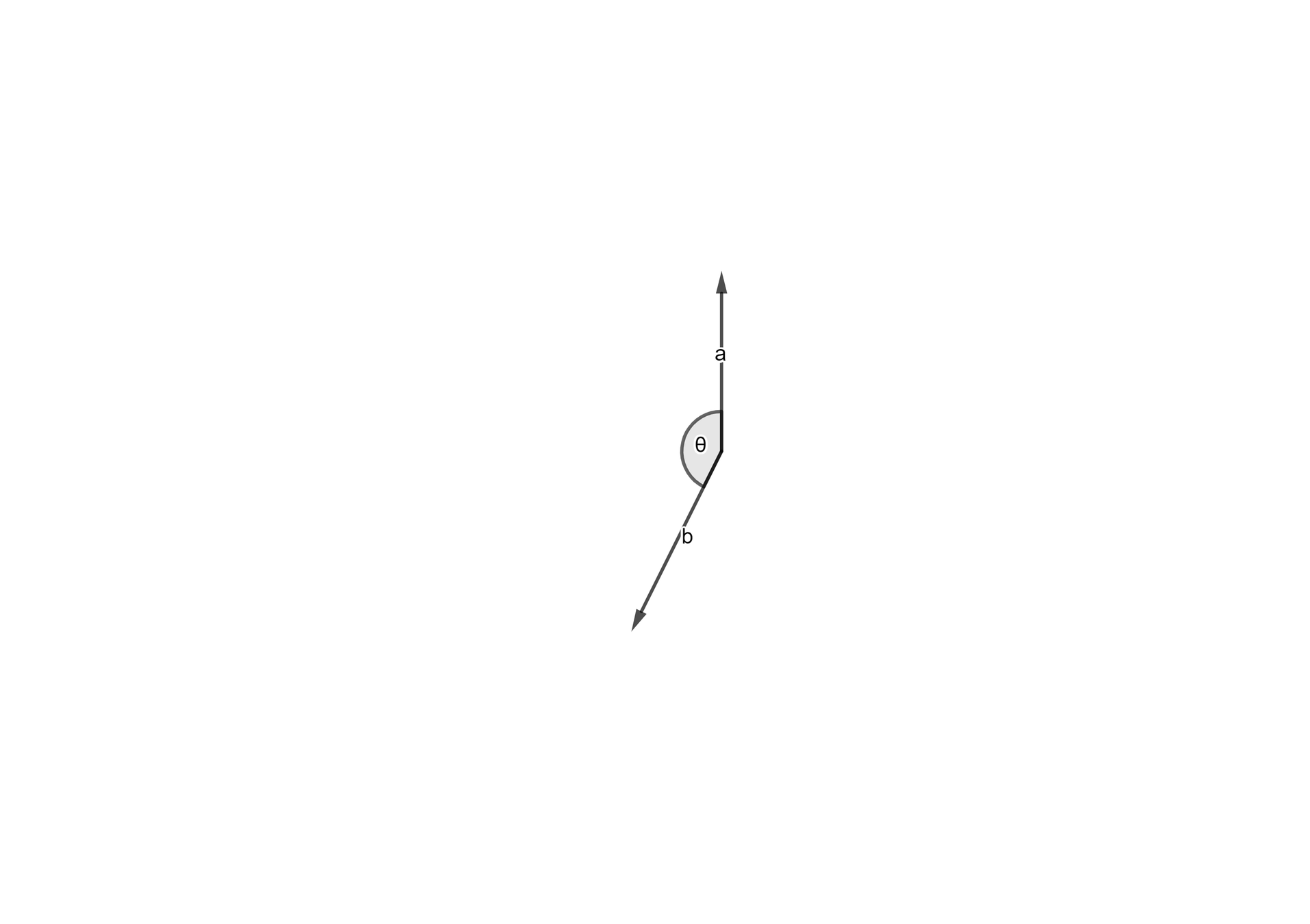
\(\theta是\vec a 逆時針轉動到\vec b的夾角\)
平面外積(行列式)
\(\begin{vmatrix}x_a & x_b \\y_a & y_b\end{vmatrix} = |\vec a||\vec b|\sin\theta\)
這邊用行列式的方式來表示
計算方式
\(\begin{vmatrix}x_a & x_b \\y_a & y_b\end{vmatrix}=x_a y_b - x_b y_a\)
\(\theta是\vec a 逆時針轉動到\vec b的夾角\)
平面外積的用處
- 判斷兩個向量的轉動方向
逆時針是正，順時針是負
- 計算面積
\(\begin{Vmatrix}x_a & x_b \\ y_a & y_b \end{Vmatrix}是\vec a和\vec b所形成的平行四邊形的面積\)
\(|\vec a|\sin\theta\)
多邊形面積
對於一個有n個點的多邊形
....
\lvert\frac 1 2 \begin{vmatrix}x_1 & x_2 \\ y_1 & y_2\end{vmatrix}+\begin{vmatrix}x_2 & x_3 \\ y_2 & y_3\end{vmatrix}
\begin{vmatrix}x_{n-1}&x_n\\y_{n-1}&y_n\end{vmatrix}+\begin{vmatrix}x_n & x_1\\y_n & y_1\end{vmatrix}\rvert
線段相交
直接算兩直線交點
可以用參數式
線段相交
有一直線\(\overleftrightarrow{AB}\)
\(\overrightarrow{AB}=(x_B - x_A, y_B - y_A)\)
對於直線\(\overleftrightarrow{AB}\)上的任一點P
\(P = A + t\overrightarrow{AB}\)
\(x_P = x_A + t(x_B - x_A)\)
\(y_P = y_A + t(y_B - y_A)\)
線段相交
如果\(\overline{AB}線段和\overline{CD}線段相交\)
\(則CD兩點要在\overline{AB}的左右兩側\)
\(則AB兩點也要在\overline{CD}的左右兩側\)
可以用外積判斷
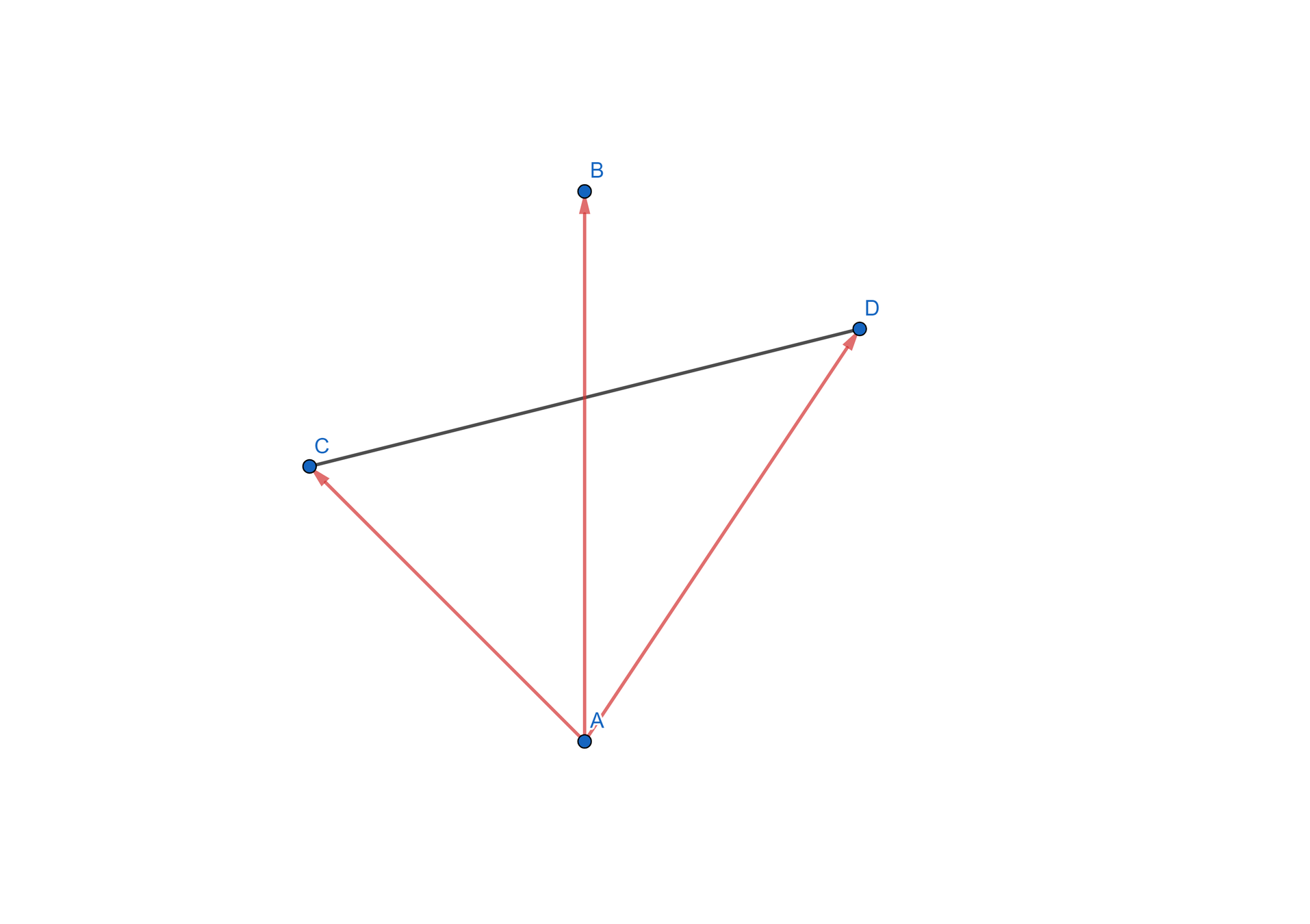
線段相交
凸包
可以包住所有點的最小凸多邊形
凸多邊形:內角小於\(180\degree\)
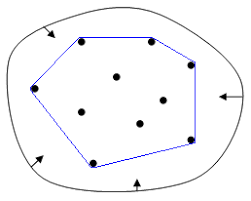
凸包
我們把凸包分成上凸包和下凸包
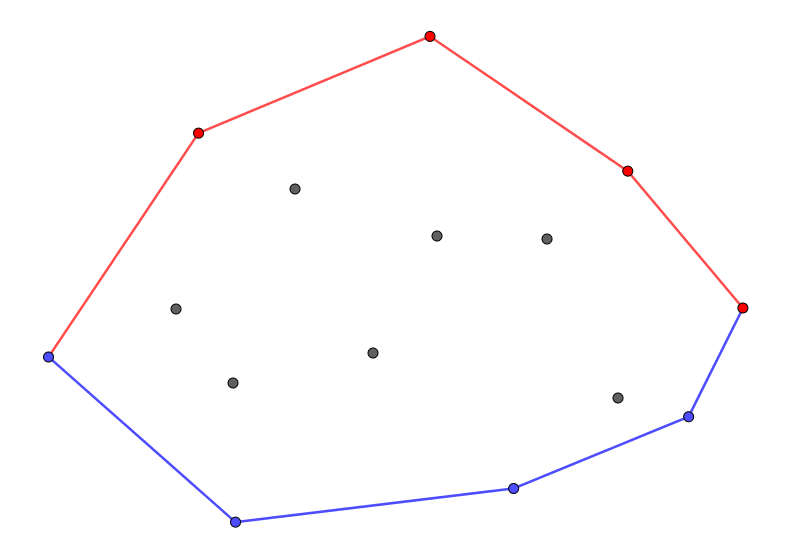
凸包
先把所有點照x座標排序
從左往右把點一個一個加進去
用一個stack來維護目前為止的凸包
A
B
每次加入時要先看最前面的兩個點
凸包
先把所有點照x座標排序
從左往右把點一個一個加進去
用一個stack來維護目前為止的凸包
B
每次加入時要先看最前面的兩個點
C
A
凸包
先把所有點照x座標排序
從左往右把點一個一個加進去
用一個stack來維護目前為止的凸包
B
每次加入時要先看最前面的兩個點
C
A
凸包
先把所有點照x座標排序
從左往右把點一個一個加進去
用一個stack來維護目前為止的凸包
每次加入時要先看最前面的兩個點
C
A
凸包
用外積判斷旋轉方向
C
A
B
可以看\(\overrightarrow{AB}和\overrightarrow{BC}的旋轉方向來判斷\)
凸包
下凸包就把排序好的點反過來再做一次
但要小心處理左右端點
凸包
下凸包就把排序好的點反過來再做一次
要小心處理左右端點
如果一邊有兩個端點
要讓上面的在上凸包
下面的在下凸包
如果只有一個端點
讓左端點在上凸包
右端點
凸包
要怎麼做到?
可以在排序時，把x座標小的放前面
如果x座標相同，把y座標大的放前面
bool cmp(pii x, pii y){
if(x.first != y.first){
return x.first < y.first;
}else{
return x.second > y.second;
}
}sort(point, point + n, cmp);
vector<pii> upconvex, downconvex;
for(int j = 0; j < n; j++){
while(upconvex.size() > 1 && cross(upconvex.back() - upconvex[upconvex.size() - 2], point[j] - upconvex.back()) >= 0){
upconvex.pop_back();
}
upconvex.push_back(point[j]);
}
upconvex.pop_back();
reverse(point, point + n);
for(int j = 0; j < n; j++){
while(downconvex.size() > 1 && cross(downconvex.back() - downconvex[downconvex.size() - 2], point[j] - downconvex.back()) >= 0){
downconvex.pop_back();
}
downconvex.push_back(point[j]);
}
downconvex.pop_back();凸包
sort(point, point + n, cmp);
vector<pii> convex;
int m = 0;
for(int i = 0; i < 2; i++){
for(int j = 0; j < n; j++){
while(convex.size() - m > 1 && cross(convex.back() - convex[convex.size() - 2], point[j] - convex.back()) >= 0){
convex.pop_back();
}
convex.push_back(point[j]);
}
convex.pop_back();
m = convex.size();
reverse(point, point + n);
}凸包
可以用同一個stack做上下凸包
凸包
極角排序
照角度排序
用一個點當作中心，把其他點照順序排成一圈
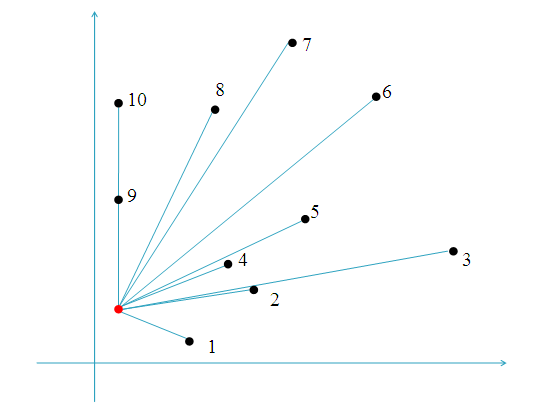
極角排序
atan2(y, x)
他會回傳從x軸正向逆時針旋轉到點(x, y)的角度\(\theta\)
在y小於0時，\(\theta\)是負的
typedef pair<int, int> pii;
bool cmp(pii a, pii b){
return atan2(a.first, a.second) < atan2(b.first, b.second);
}極角排序
外積
用外積判斷旋轉方向
記得先判y的正負
bool cross(pii a, pii b){
return a.first * b.second - a.second * b.first;
}
bool cmp(pii a, pii b){
bool c = (a.second > 0 || (a.second == 0 && a.first > 0));
bool d = (b.second > 0 || (b.second == 0 && b.second > 0));
if(c != d)
return c > d;
return cross(a, b) < 0;
}計算幾何
By scottchou
