進階資料結構
線段樹
詢問區間[l, r]的和
把區間切成很多塊
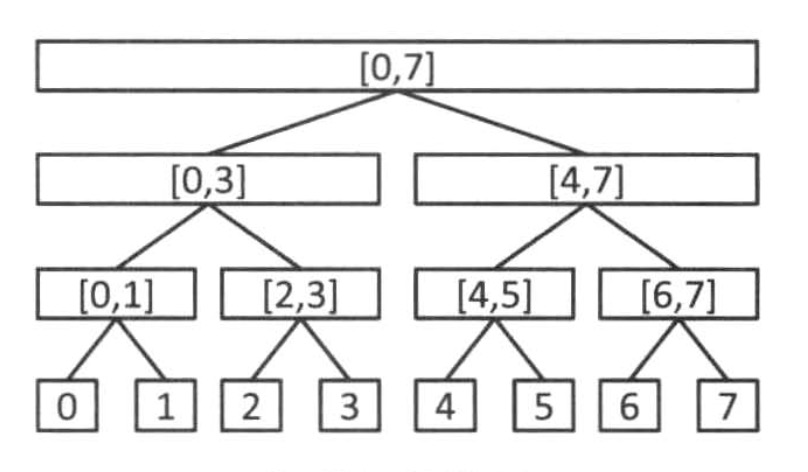
透過這種分割方式
對於一個詢問,可以把它拆成多個線段樹上的節點

例:[0, 6]
線段樹節點的編號
可以用二元樹的方式編號
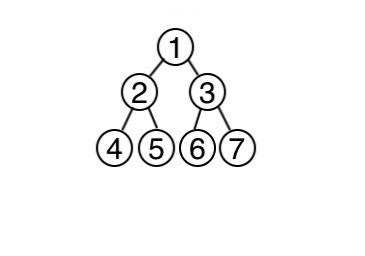
根結點的邊號為1
對一個節點,編號為\(i\)
他的左子節點編號為\(2\times i\)
他的右子節點編號為\(2\times i + 1\)
線段樹節點的編號
也可以隨便編號
但每個節點就要額外紀錄
他的左右子節點的編號
線段樹節點的編號
或是用指標
你就不需要編號了
建樹的code
void build(int v, int ll, int rr) {
if (ll == rr) {
node[v] = a[ll];
return;
}
int mid = (ll + rr) / 2;
build(v * 2, ll, mid);
build(v * 2 + 1, mid + 1, rr);
node[v] = node[v * 2] + node[v * 2 + 1];
}詢問[ql, qr]的和
int query(int ql, int qr, int v, int ll, int rr) {
if (ql == ll && qr == rr) {
return node[v];
}
int mid = ll + rr >> 1;
if (qr <= mid)
return query(ql, qr, v * 2, ll, mid);
else if (ql > mid)
return query(ql, qr, v * 2 + 1, mid + 1, rr);
else
return query(ql, mid, v * 2, ll, mid) + query(mid + 1, rr, v * 2 + 1, mid + 1, rr);
}單點修改
把a[i]的值改成x
找到他在線段樹中最底層的結點
修改他的值
在將有覆蓋到他的區間
由下而上的更新

例:修改a[5]
區間修改
一個一個改太浪費時間
懶人標記
碰到整個區間都要修改,
直接標記起來就好
之後碰到在往下推

int const N = 1e5;
struct Node {
int sum, lazy_add = 0;
}node[N << 2];
int n;
void push(int v, int ll, int rr) {
if (node[v].lazy_add) {
int mid = ll + rr >> 1;
node[v << 1].sum += (mid - ll + 1) * node[v].lazy_add;
node[v << 1 | 1].sum += (rr - mid) * node[v].lazy_add;
node[v << 1].lazy_add += node[v].lazy_add;
node[v << 1 | 1].lazy_add += node[v].lazy_add;
node[v].lazy_add = 0;
}
}
void modify(int ml, int mr, int val, int v = 1, int ll = 1, int rr = n) {
if (ml == ll && mr == rr) {
node[v].lazy_add += val;
return;
}
int mid = ll + rr >> 1;
push(v, ll, rr);
if (mr <= mid)
modify(ml, mr, val, v << 1, ll, mid);
else if (ml > mid)
modify(ml, mr, val, v << 1 | 1, mid + 1, rr);
else {
modify(ml, mid, val, v << 1, ll, mid);
modify(mid + 1, mr, val, v << 1 | 1, mid + 1, rr);
}
node[v].sum = node[v << 1].sum + node[v << 1 | 1].sum;
}
int query(int ql, int qr, int v, int ll, int rr) {
if (ql == ll && qr == rr)
return node[v].sum;
int mid = ll + rr >> 1;
push(v, ll, rr);
if (qr <= mid)
return query(ql, qr, v << 1, ll, mid);
else if (ql > mid)
return query(ql, qr, v << 1 | 1, mid + 1, rr);
else
return query(ql, mid, v << 1, ll, mid) + query(mid + 1, qr, v << 1 | 1, mid + 1, rr);
}BIT
binary indexed tree
支援的操作
- 單點加值
- 區間和(前綴和)
int bit[200005], n;
int lowbit(int x) {
return x & (-x);
}
int query(int x) {
int sum = 0;
while (x > 0) {
sum += bit[x];
x -= lowbit(x);
}
return sum;
}
void modify(int x, int val) {
while (x <= n) {
bit[x] += val;
x += lowbit(x);
}
}區間加值單點查詢
區間加值單點查詢
差分陣列
例題:
進階題:
Sparse Table
倍增表
Sparse Table
用於處理各種區間問題
(最大最小值、最大公因數、區間和)
deck
By scottchou
deck
- 152



