Algoritmia y Programación II
public class Main{
public static void main(String[] args){
System.out.println("Welcome to AYP2!")
}
}
if __name__ == '__main__':
print("Welcome to AYP2!")Contenido de la presentación
public class ContenidoDeLaPresentacion{
public static void main(){
System.out.println("Descripción del curso 📎");
System.out.println("Profesor (sobre mí) 👨🏼🏫");
System.out.println("Estudiantes (sobre ustedes)🧑🏻🎓👩🏻🎓");
System.out.println("Objetivo general del curso");
System.out.println("Contenido del curso");
System.out.println("Calificaciones");
System.out.println("Textos de referencia");
System.out.println("Fundamentos");
System.out.println("Estructuras Estáticas: vectores ");
System.out.println("Estructuras Estáticas: Matrices");
System.out.println("Cadenas");
System.out.println("Recursividad");
}
}Descripción del curso
Nombre: Algoritmia y Programación II
NRC:
Créditos: 3
Horas de atención: con cita
Profesor (sobre mí)
- Ing. Sebastian David Ariza Coll de la Universidad del Norte
- M.Sc. de la Universidad del Norte
-
Temas de investigación:
- Inteligencia artificial (Machine Learning)
- Weather Forecasting
- Data Assimilation
- Analista de Inteligencia de Datos
Email: sdariza@uninorte.edu.co
Estudiantes (sobre ustedes)
- Nombre
- Experiencia previa en: Java/Python, estructuras estáticas, paradigma procedimental, recursividad.
- Expectativas acerca del curso
Objetivo general del curso
Diseñar algoritmos que impliquen la utilización de Estructura de Datos estáticas, funciones, subrutinas, recursividad y operaciones con cadena de caracteres en al menos un lenguaje de programación.
S06. Habilidad para desarrollar y llevar a cabo experimentación adecuada, analizar e interpretar datos, y usar el juicio de ingeniería para sacar conclusiones.
Contenido I
Estructuras estáticas
- Arreglos unidimensionales (vectores) {Semanas 1 a 2}
- Operaciones, ejemplos, ejercicios.
- Arreglos bidimensionales (matrices) {Semanas 3 a 4}
- Operaciones, ejemplos, ejercicios.
- Cadenas {Semanas 5 a 6}
- Operaciones, ejemplos, ejercicios.
Contenido II
Paradigma procedimental
- Subrutinas y funciones {Semanas 7 a 10}
Recursividad
- Concepto de recursividad {Semanas 10 a 12}
- Pilas y colas {Semanas 12 a 14}
Calificaciones
| Evaluación | % | Fecha | Temas |
|---|---|---|---|
| Parcial 1 | 25 | Semana 6 | Estructuras estáticas 1 y 2 |
| Laboratorio 1 | 15 | Semana 10 | Estructuras estáticas todas. |
| Parcial 2 | 20 | Semana 12 | Estructuras estáticas 3, procedimientos. |
| Laboratorio 2 | 10 | Semana 11-16 | Procedimientos y recursividad |
| Proyecto/Presentación | 10 | Semana 14 | Todo |
| Parcial Final | 20 | Según registro | Todo - Departamental |
Textos de Referencia y páginas web de interés
- Jabba, Daladier. Manual de Informática II. Primera edición Ediciones Uninorte 2000.
- Joyanes Aguilar Luis. Fundamentos de Programación. Cuarta Edición. 2008.
Textos de Referencia y páginas web de interés
- https://www.geeksforgeeks.org/python-programming-language/?ref=shm
- https://www.geeksforgeeks.org/java/?ref=shm
- https://www.geeksforgeeks.org/array-data-structure/?ref=shm
- https://www.geeksforgeeks.org/matrix/?ref=shm
- https://www.geeksforgeeks.org/string-data-structure/?ref=shm
- https://www.geeksforgeeks.org/introduction-to-recursion-data-structure-and-algorithm-tutorials/
Fundamentos
¿Algoritmo?
Durante la infancia, desarrollamos las bases de nuestra estructura lógica mediante interacciones con el entorno. Una vez establecida esta lógica, la utilizamos para llevar a cabo procesos cotidianos, tanto conscientes como inconscientes, desde operaciones matemáticas hasta actividades como hablar, leer y caminar.
Asimismo, estos procesos están formalizados en algoritmos, representaciones conscientes de la lógica que nos guían en nuestras acciones. Los algoritmos nos permiten describir los procesos de manera que cualquier persona, incluso sin conocimiento previo, pueda llevarlos a cabo con éxito.
¿Qué es un algoritmo?
Definición formal: "Un algoritmo es un conjunto de pasos lógicos sin ambigüedad que permiten la realización de un proceso en un tiempo finito".
Por ejemplo: tome la operación aritmética formal de la suma. Suponga que desea sumar dos número. ¿Qué cree que debe hacer?
Lo anterior parece un proceso lógico, ¿cierto? Tenga presente que todos los algoritmos lo son. Una vez formalizado el proceso lógico para la realización de una tarea, este puede ser entendido en forma fácil por cualquier persona.
Sin embargo el proceso para la formulación de la lógica es lo que resulta inicialmente difícil en el aprendizaje de los algoritmos.
Algoritmos en la vida diaria
Suponga que usted está frente a una escalera y desea ascender hasta llegar al final. ¿ Qué haría usted? Es decir, ¿cuál es el proceso lógico que debe realizar para alcanzar su objetivo?
La forma detallada de analizar todos los eventos es lo que conforma un algoritmo.
Algoritmos en la vida diaria
Tomemos otro ejemplo, suponga ahora que usted desea beber un vaso con agua. ¿Cuál sería el algoritmo?
Algoritmos en la vida diaria
Del ejemplo anterior, note que el solo hecho de dirigirse a la nevera es un proceso mucho más complejo que el de subir una escalera. Ya que el desplazamiento dependerá de cuán alejado se esté de la nevera y hayan más obstáculos que nos separen de ella.
Algoritmos en la vida diaria
Ejercicios propuestos
Escriba los algoritmos necesarios para realizar los siguientes procesos:
- Cambiar la llanta a un automóvil.
- Escribir la letra E en un papel.
- Preparar una limonada.
- Calcular 10 elevado a 10.
- Cenar.
- Seleccionar un lugar a dónde ir.
Variables
Variables
Cada vez que se necesite realizar un proceso es necesario conocer:
- ¿Cuál es el proceso?
- Los datos que se necesitan para la realización de dicho proceso.
- ¿Qué se debe obtener de estos datos? (Finalidad)
Sin embargo todos estos elementos son almacenados en memoria. Similar a nosotros, los sistemas de computación poseen una memoria electrónica, lugar en el cual pueden almacenar sus procesos, datos e información generada.
Imagínese esa memoria como una serie de casillas, cada una de las cuales tiene asociada una posición de la memoria.
Debido a que usted está en la capacidad de cambiar el valor almacenado dentro de cada casilla en cualquier momento, a estas casillas se les denomina variables. Con lo que una variable es una posición de memoria en el computador en el cual puede almacenar un dato o una información.
| 50 |
| 30 |
| 20 |
| 'casa' |
| vec[1] = 1 |
| vec[2] = 10 |
| vec[3] =2 |
| '0' |
Variables
Para facilitar el manejo de estas variables, a cada una de ellas se les asocia un nombre o identificador, el cual tiene unas reglas que se detallan a continuación:
- Deben comenzar con una letra
- La primera letra debe ser seguida por letras o dígitos, cero o más veces.
- El caracter " " no es ni letra ni dígito, por lo que no puede formar parte de ningún nombre de variable. Es decir el nombre de una variable necesariamente debe ser una sola palabra.
Ejemplos:
| Nombre de variable | Validez |
|---|---|
| A | ✅ |
| A123C | ✅ |
| A BVC | ❌ No es una sola palabra |
| NUM-X | ❌ Caracter "-" |
| sw | ✅ |
Tipos de variables
- Numéricas: Solo almacenan valores numéricos. Pueden ser de dos tipos:
- Enteros: Solo se almacenan valores enteros
- Reales: Puede almacenar cualquier valor numérico real.
- Alfanuméricas: Puede almacenar cualquier caracter, sin importar que sea dígito, letra o algún caracter especial.
- Lógicas: Solo puede almacenar dos posibles valores: Verdadero (True) o Falso (False).
Ejercicios propuestos
Determine cuál de los siguientes elementos son o no nombres válidos para variables
| Nombre de variable | Validez |
|---|---|
| 123AXT | |
| LadoX | |
| --XYX | |
| A*VA | |
| NUM |
Primitivas Algorítmicas
Primitiva Inicio - Fin
Primitiva de asignación o adjudicación de datos
Primitiva de entra y salida
Inicio
|
|... Proceso lógico
|
Finvariable <--- valorLEA v1, V2, V3, ... , Vn
ESCRIBA valor_a_escribirPrimitiva para bloques condicionales NO repetitivos
SI (condición) ENTONCES
Instrucción 1
Instrucción 2
Instrucción 3
...
Instrucción n
SINO
Instrucción 1
Instrucción 2
Instrucción 3
...
Instrucción m
FinEjemplo:
Calcule las raíces de un polinomio cuadrático
INICIO
Real a,b,c, r1, r2
LEA a,b,c
d <--- b^2-4*a*c
SI (d<0) ENT
Esc('El polinomio no tiene raíces en x')
SINO
r1 <--- (-b + d^0.5)/2*a
r2 <--- (-b - d^0.5)/2*a
Esc('x1:', r1)
Esc('x2:', r2)
FIN-SI
FINEjemplo:
Haga un algoritmo para calcular el valor de la función f(x), para cualquier valor de x, si la función es:
Primitiva bloque condicional modificada (Dependiendo de)
DD expresión HAGA
VALOR1: BLOQUE DE INSTRUCCIÓN 1
VALOR2: BLOQUE DE INSTRUCCIÓN 2
...
VALORn: BLOQUE DE INSTRUCCIÓN n
Ow:
Bloque de instrucciones
FIN-DDEjemplo:
- Suponga una expresión de la forma:
OPERANDO OPERADOR OPERANDO.
Donde el operador puede ser: +, -, *, /
Se desea hacer un algoritmo que permita evaluar una expresión que presente la anterior característica.
Ejercicio propuesto
Suponga que el sueldo básico de los trabajadores es:
S = HT * 2500 + 5000
Donde, HT: horas trabajadas.
Al sueldo debe descontarse una cuota de seguro social. Este descuento varía de acuerdo con el tipo de empleado asegurado, digamos:
| Tipo de empleo | Descuento |
|---|---|
| 1 | $3.000 |
| 2 | $2.000 |
| 3 | $1.500 |
| 4 | $1.000 |
Diseñe un algoritmo que dadas las horas de trabajo y el tipo de empleado calcule el sueldo que se debe pagar a un empleado asegurado.
Primitivas procesos repetitivos
MQ (condición) HAGA
Instrucción 1
Instrucción 2
...
Instrucción n
FIN-MQPrimitiva mientras que
Lógicamente esta primitiva verifica la condición que controla el ciclo y las instrucciones encerradas dentro de la estructura son ejecutadas MIENTRAS QUE la condición se cumpla, o sea mientras el valor lógico de esta sea verdadero.
Ejemplo
Considere el ejemplo sobre calcular las raíces a un polinomio cuadrático. El objetivo ahora es dados N polinomios cuadráticos, se debe calcular sus raíces reales siempre y cuando sea posible.
Ejercicios propuestos
- Haga un algoritmo que calcule e imprima todos los divisores de un número entero N > 0 dado.
- Haga un algoritmo para determinar si un número entero N > 0 dado es primo.
- Haga un algoritmo para calcular todos los números primos entre 1 y 100
Primitiva cíclica con base en un contador
Esta primitiva cíclica trabaja con base en una variable contador, la cual va a cambiar dentro de un rango posible de valores que es especificado como parte de la estructura
A diferencia con el MQ, las instrucciones dentro del ciclo se ejecutan mínimo 1 vez.
PARA (contador<---<V.inicial>, <V.final>, <inc>) HAGA
Instrucción 1
Instrucción 2
...
Instrucción n
FIN-PARAEjemplo
Utilizando el descubrimiento de la fórmula del Dr. Matiz, genere los N primeros términos de la sucesión.
Ejercicio propuesto
La función sen(x) puede ser aproximada mediante la siguiente serie:
Haga un algoritmo que para un valor x y un n dado, calcule una aproximación a la función sen(x).
Nota: El factorial no es una operación predefinida, por tanto debe ser calculada para cada uno de los elementos de la serie. Suponga que el x está en radianes
Ejercicio propuesto
La sucesión de Fibonacci puede ser generada mediante la siguiente función
Haga un algoritmo para calcular el n-ésimo término de la sucesión de Fibonacci.
Contenido I
Estructuras estáticas
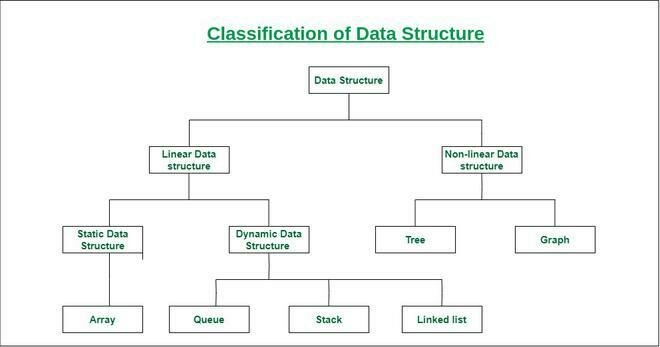
Arreglos unidimensionales
Arreglos unidimensionales
Variables arreglo
En las secciones anteriores se ha venido trabajando con base en variables que solo pueden almacenar un valor. Las variables arreglos tienen como característica principal el hecho que pueden almacenar un gran número posibles de valores, con la única restricción que todos ellos deben ser necesariamente del mismo tipo.
Para diferenciar cada uno de los valores que estén almacenados en una variable arreglo, estos son numerados y su posición es indicada mediante un índice como parte del nombre de la variable.
Manejo de vectores
Dependiendo del número de subíndices asociados a las variables arreglo, estas se clasifican en uni, bi, o n-dimensional.
Los arreglos de una dimensión son comúnmente llamados Vectores, los cuales a nivel interno, se encuentran en una secuencia lineal de variables simples, por lo que también se les llama Arreglos lineales. A estos arreglos se les referencia colocando el nombre del vector, seguido de un par de paréntesis donde está guardado el índice que designa la variable del arreglo a referenciar.
Es decir, su sintaxis es:
Vec(i) ó Vec[i]
Donde:
Vec: es el nombre del vector.
i: variable que referencia la posición i-ésima del vector.
| 34 | 565 | 453 | 13 | 4 | 892 | 88 | 86 | 23 | 3 |
|---|
a
Representación visual
i
Se tiene un vector con:
- 10 elementos
- Es de tipo entero
- El nombre es a
- i referencia la posición sobre a
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|
Lectura de un vector unidimensional
INICIO
| ENTERO: vec(100), n <-- 0
| MQ(n < 1 ó n > 100)
| | LEA N
| FIN-MQ
|
| PARA(i <-- 0, n-1, 1) HAGA
| | LEA vec(i)
| FIN-PARA
FINEscritura de un vector unidimensional
INICIO
| ENTERO: vec(100), n <-- 0
| MQ(n < 1 ó n > 100)
| | LEA N
| FIN-MQ
| PARA(i <-- 0, n-1, 1) HAGA
| | LEA vec(i)
| FIN-PARA
| PARA(i <-- 0, n-1, 1) HAGA
| | ESC vec(i)
| FIN-PARA
FINBúsqueda secuencial en un vector
| 34 | 565 | 453 | 13 | 4 | 892 | 88 | 86 | 23 | 3 |
|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|
vec
x = 892
- El vector tiene n elementos NO repetidos
- Se desea buscar el elemento x
- Se debe recorrer desde la posición 0 hasta la posición n-1 e ir preguntando si vec[i] = x, en caso verdadero indicar que se ha encontrado el elemento en posición i y detener la búsqueda
- Mejor caso:
- Peor caso:
- Complejidad:
Eliminación de un elemento
Dado un vector v con n elementos, realice un algoritmo para eliminar el elemento x si existe.
Suponga que el vector NO tiene elementos repetidos
| 3 | 4 | 5 | 23 | 45 | 245 | 1 | 10 |
|---|
v
i
Vector de entrada
v
i
Vector resultante, si x = 2
| 3 | 4 | 5 | 23 | 45 | 245 | 1 | 10 |
|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|
| 0 |
|---|
- En la eliminación hay una búsqueda implícita.
- Casos si el elemento es encontrado en posición pos:
- Caso 1: El elemento está en : v(pos) pasa a v(pos+1)
- Caso 2: El elemento está en : v(pos) = 0
- Una vez el elemento es eliminado, el vector queda con dimensión n-1
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|
Inserción de un elemento
Dado un vector v con n elementos, realice un algoritmo para insertar el elemento x en posición k.
| 3 | 4 | 5 | 23 | 45 | 245 | 2 | 1 | 10 |
|---|
v
i
Vector de entrada
v
i
Vector resultante, x = 50, k = 2
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|
| 50 |
|---|
¡Quiz!
| 3 | 4 |
|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|
| 5 | 23 | 45 | 245 | 2 | 1 | 10 |
|---|
Ejercicios complementarios
- Lea un vector de n elementos e indique el valor de la suma de todos los valores del mismo.
- Sea un vector "v" de n elementos, desarrolle un algoritmo que encuentre el mayor elemento.
- Sea un vector "x" de n elementos, desarrolle un algoritmo que lo ordene de forma ascendente: https://www.chrislaux.com/miscsort
- Sean 2 vectores "a" y "b", desarrolle un algoritmo que calcule la operación a + b si es posible.
- Sean 2 vectores "a" y "b" de dimensión n, realice un algoritmo que calcule
- Desarrolle un programa que acepte la entrada de un vector con N elementos. Luego, realice una inversión de todos los elementos de tal manera que el primer elemento pase a ser el último, el último se convierta en el primero, el segundo elemento se coloque en la posición penúltima, y así sucesivamente hasta completar la reordenación de todos los elementos.
- Haga un algoritmo para almacenar en un vector x los factores primos de un n dado.
Ejercicio propuesto
La sucesión de Fibonacci puede ser generada mediante la siguiente función
Haga un algoritmo que almacene en un vector todos los términos de la sucesión de Fibonacci hasta un n dado.
| 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 |
|---|
fib
i
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|
Ejercicio propuesto
Represente en dos vectores los dígitos de dos números enteros cualquiera, en un vector resultante almacena la operación suma
| 3 | 4 | 5 | 2 | 2 | 7 | 2 | 1 | 9 |
|---|
x
Vectores de entrada
| 1 | 0 | 9 | 0 | 7 | 3 | 9 | 2 | 3 | 4 |
|---|
sum
Vector resultante
| 7 | 4 | 5 | 5 | 1 | 2 | 0 | 1 | 5 |
|---|
y
Nota: cada dígito es positivo, recuerde que 0 a la izquierda no se tienen en cuenta.
Ejercicio propuesto
Un número se considera palíndromo si se lee exactamente igual de izquierda a derecha. Haga un algoritmo que para un entero n dado, almacene sus dígitos en un vector v y diga si el número es o no palíndromo. Nota: No se permite usar cadenas de caracteres ni la función
n=6556
| 6 | 5 | 5 | 6 |
|---|
V
Evaluación de un polinomio
Unión de vectores
Ejercicio
Ejercicio
Ejercicio propuesto
En una carrera de n caballos enumerados del 1 al n se registran en un vector c el número de las vueltas realizadas por cada uno de los caballos, en un vector t (paralelo al c) se registran los tiempos en segundos para cada carrera registrada en c en el mismo orden con que se ingresan en c. Realice un pseudocódigo para determinar:

1. ¿Qué caballo fue el ganador de las carreras?
- Debió terminar todas las vueltas
2. ¿Cuál es el tiempo promedio para el ganador de las carreras?
3. Indique para los 10 primeros puestos el número del caballo y el tiempo promedio de sus carreras.
4. ¿Cuál fue el promedio de los tiempos en general?
Arreglos bidimensionales
Variable matriz
Pudimos notar que un vector es una variable conformada por la unión de una serie de variables sencillas; sin embargo este arreglo a su vez es una variable.
La forma de unir variables para conformar una variable arreglo hace que se puedan formar variables cuyos elementos sean variables vectores y no variables sencillas; a esto lo conocemos como una variable matriz.
Una matriz es entonces un vector cuyos elementos son vectores. Esta característica, en este tipo de arreglo, hace que dicha variable requiera de dos subíndices para poder direccionar uno de sus elementos: uno para indicar el vector de la matriz (llamado normalmente fila) y el otro para indicar el elemento dentro de ese vector (denominado columna).
Representación - Variable matriz
La notación para este tipo de variable es: Primero el nombre de la matriz, seguido por paréntesis donde se encuentran los dos índices separados por una coma. (Por lo general, el primer índice indica fila del arreglo bidimensional, y el segundo indica la columna del arreglo). Su sintaxis es:
Mat(i,j) donde:
Mat: es el nombre de la matriz.
i,j: son la variables que referencia la fila i y la columna j.
Representación - Variable matriz

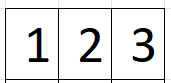
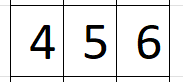
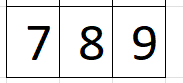
Diagonal principal
Sea M una matriz cuadrada de dimensión nxn, imprima todos los elementos de la diagonal principal
Transpuesta - Diagonal principal
Sea M una matriz cuadrada de dimensión nxn, calcule la transpuesta por la diagonal principal. No se permiten vectores ni matrices auxiliares.
Sea M una matriz cuadrada de dimensión nxn, imprima todos los elementos de la diagonal secundaria. No se permiten vectores ni matrices auxiliares.
Transpuesta - Diagonal secundaria
Sea M una matriz cuadrada de dimensión nxn, imprima todos los elementos de la triangular superior sin incluir la diagonal principal
Triangular superior
Triangular inferior
Sea M una matriz cuadrada de dimensión nxn, imprima todos los elementos de la triangular inferior sin incluir la diagonal principal
Ordenamiento de una Matriz
Sea M una matriz de dimensión nxm, desarrolle un algoritmo para ordenarla de forma ascendente. Debe hacer el análisis de tal forma que se realice el menor número de comparaciones teniendo en cuenta en cuenta el método de burbuja.

Ejercicio propuesto
Sea M una matriz cuadrada de dimensión nxn, determine si es simétrica. Es decir, se cumple que
Multiplicación de Matrices
Concatenación
Concatenación
Matriz caracol

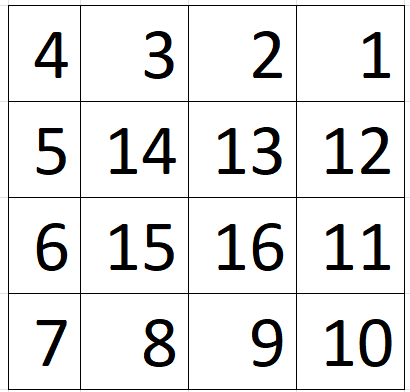
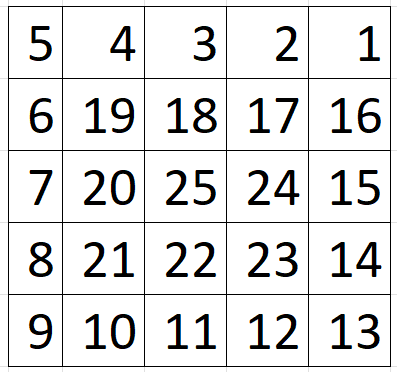
n=3
n=4
n=5
Triángulo de Pascal
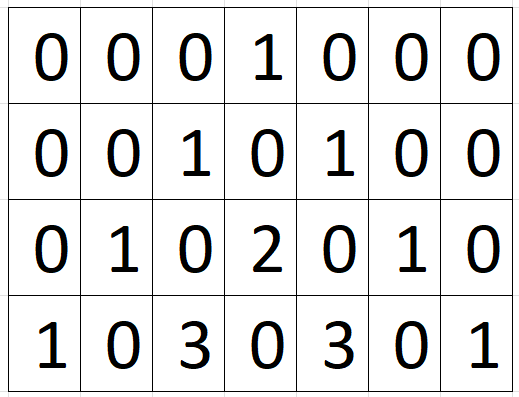
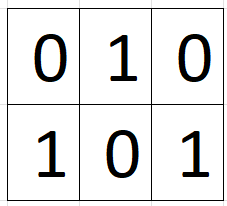
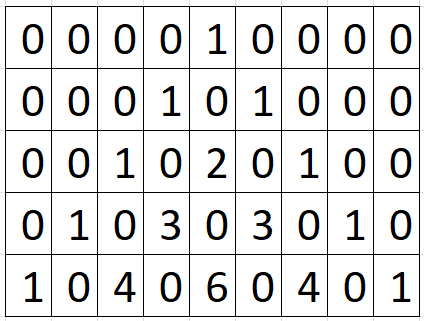
Matriz zigzag
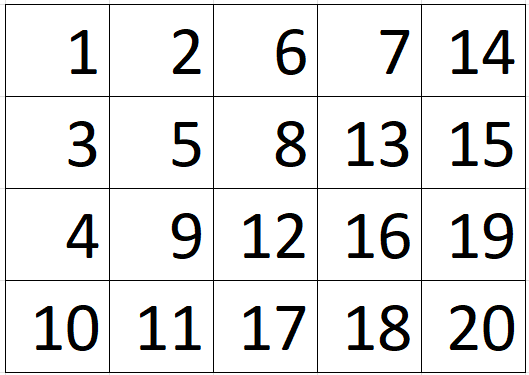
Cadenas
Cadena de caracteres
Hasta el momento, la información almacenada y procesada en las variables ha sido de tipo numérico.
Los valores de variables que pueden contener cualquier serie de caracteres son denominadas CADENAS o STRING; y, por lo general, pueden incluir cualquier carácter del conjunto de caracteres manejados por el equipo en particular que se tenga; aunque, los más común es que solo se considere letras y números.
Las variables que almacenan información de esta clase se usan en algoritmos de la misma forma que las de tipo numérico.
La forma en que se almacena la información es mediante comillas.
Cadena de caracteres
Ejemplo
Se desea almacenar la palabra: Algoritmos en la variable x. Por tanto la forma correcta de hacerlo sería:
Note que de hacerse la asignación de la forma:
Se entenderá que a x se le está asignando el valor de una variable llamada Algoritmos.
Operaciones básicas
Concatenación (+)
Esta operación trata de de unir dos más cadenas de caracteres en una sola.
Ejemplo
Suponga que X, Y y Z son variables de caracteres y que X contiene los caracteres "PRÓXIMA", Y tiene "PARADA".
Se puede alojar en la variable Z los caracteres con la oración "PRÓXIMA PARADA".
Sin embargo si usted solo indica
Esto generará la palabra: "PRÓXIMAPARADA".
Con lo que, si usted desea separar las frases por espacio deberá adicionar el caracter espacio " " como sigue:
Note que : X+Y NO es igual a Y+X
Longitud
LONG(cadena:String)
Esta operación arroja el tamaño actual de la cadena, es decir cuántos caracteres se encuentran almacenados.
Ejemplo
Inicio
z <-- "Universidad"
Escriba(LONG(z))
FINSe escribirá en pantalla el número 11.
Obtención de subcadenas
Ejemplo:
c <-- "Hola a todxs"
subsIzq <-- IZQ(c,6)
ESC(subsIzq)// escribirá "Hola a"
Operación IZQ(cadena:String, n_caracteres:Integer)
Extrae n caracteres empezando desde la izquierda y en el mismo orden en que se encuentren
Obtención de subcadenas
Ejemplo:
c <-- "Hola a todxs"
subsDer <-- DER(c,6)
ESC(subsDer)// escribirá " todxs"
Operación DER(cadena:String, n_caracteres:Integer)
Extrae n caracteres empezando desde la derecha y en el mismo orden en que se encuentren
Obtención de subcadenas
Esta función extrae una subcadena de n caracteres hacia la derecha mediante la función SUBSTR.
Tiene 3 argumentos: el nombre de la variable, la posición inicial y la longitud de la subcadena.
Ejemplo:
SUBSTR(cadena:String, pos_inicial:Integer, n_caracteres:Integer)
c <-- "Hola a todxs"
subs <-- SUBSTR(c, 0,3)
ESC(subs)// escribirá "Hol"
Obtención de carácter
Esta función extrae un único carácter dependiendo de la posición que se le indique mediante la función CARACTER(cadena, pos).
Tiene 2 argumentos: el nombre de la variable, la posición.
Ejemplo:
CARACTER(cadena:String, pos:Integer)
c <-- "Hola a todxs"
caracter <-- CARACTER(c, 3)
ESC(caracter)// escribirá 'l'
Cadena a valor numérico
VAL(cadena:String)
Esta operación convierte una cadena alfanumérica número entero, siempre y cuando la cadena solo contenga dígitos numéricos enteros.
Ejemplo
Inicio
z <-- "612"
Esc(VAL(z)) // Escribirá 612 como número entero
FINValor numérico a alfanumérico
STR(num:float,integer)
Esta operación convierte un número a cadena, no importa si es decimal o entero.
Ejemplo
Inicio
z <-- 3.1415
Esc(STR(z)) // Escribirá "3.1415" como cadena
FINFunción ASCII
ASCII(caracter:caracter)
Esta operación convierte un carácter en su respectiva representación numérica
Ejemplo
Inicio
z <-- 'a'
Esc(ASCII(z)) // Escribirá 97 como número entero.
FINEnlace para más detalles: https://elcodigoascii.com.ar/
Función Mayúscula
Mayúscula(cadena:String)
Esta operación convierte todas letras de una cadena en mayúsculas.
Ejemplo
Inicio
z <-- "Hola amig@s"
Esc(Mayuscula(z)) // Escribirá "HOLA AMIG@S"
FINFunción Minúscula
Minúscula(cadena:String)
Esta operación convierte todas letras de una cadena en minúsculas.
Ejemplo
Inicio
z <-- "Hola amig@s"
Esc(Minuscula(z)) // Escribirá "hola amig@s"
FINEjemplos
Sea n un número entero, diga cuántos dígitos son pares.
Ejemplos
Se dice que una cadena de caracteres es palíndrome si de derecha a izquierda se lee exactamente igual que de izquierda a derecha.
Haga un algoritmo para leer una cadena de caracteres y determinar si es o no palíndrome.
Nota: La cadena puede tener espacios vacíos. Debe eliminarlos.
Ejemplos
Sean a y b dos cadenas de caracteres. Compárelas y determine cuál de las dos tiene mayor número de vocales.
Ejemplos
Haga un algoritmo para verificar si un número entero positivo como cadena está bien escrito
Ejemplos
Haga un algoritmo para verificar si una cadena de caracteres leída es un número decimal. Suponga que solo verificará números de la siguiente forma:
"1.233"
"0.2321"
"10.2123"
"10.0"
Ejemplos
Haga un algoritmo para pasar un número entero de base 10 a base 11.
Subprogramas
o
Procedimientos
Introducción a los subprogramas o procedimientos
Cuando los problemas son muy complejos de resolver, es necesario fraccionarlos en subproblemas y abordar cada uno de ellos por separado, y no tratarlos como un todo.
Es por ello, que surge la necesidad de trabajar con un esquema de programación un poco diferente al que se ha venido manejando, y al cual denominaremos "solución de problemas mediante subalgoritmos o subprogramas (procedimientos)". Teniendo así el término divide y vencerás.
Introducción a los subprogramas o procedimientos
Es importante mencionar que el uso de procedimientos nos permite localizar errores y corregirlos de una forma más fácil y sin preocuparse por el resto del algoritmo, ya que cada procedimiento es totalmente independiente de los otros.
Asimismo, el uso de subpragramas evita la repetición de líneas o bucles de instrucciones dentro del algoritmo. Ejemplo de esto es si usted desea calcular la operación sobre las matrices A y B.
(A+B)B ó (A-B)A
Note que ambos casos se desea realizar un producto de matrices independientemente a la suma y/o resta.
Introducción a los subprogramas o procedimientos
A este tipo de programación también se le conoce como "programación modular", la cual presenta 2 formas:
- Subprogramas: indica que cada uno de los procedimientos es un programa o archivo y existe un programa principal que se encargará de decidir cuáles y en qué orden se van a ejecutar.
- Procedimientos: indica que en un mismo archivo o programa estarán todos los procedimientos junto con el algoritmo principal, el cual se encargará de decidir cuáles procedimientos y en qué orden se ejecutarán.
Por comodidad, trabajaremos con procedimientos.
Procedimientos
Cuando se trabaja con el esquema de procedimientos, es importante destacar que cada uno de ellos es un algoritmo con un propósito en específico, en los cuales se pueden leer o escribir datos.
Los procedimientos, de manera general, aceptarán datos, realizarán cálculos y devolverán resultados, razón por la cual deberán contar con unas condiciones iniciales que estarán dadas por lo comúnmente llamado "parámetros".
Además, un procedimiento puede ser llamado desde otro algoritmo principal o desde otro procedimiento.
Procedimientos
Es importante tener en cuenta que una vez invocado un procedimiento, este se ejecutará por completo y devolverá el control, junto con los resultados, a quien lo haya invocado, que pudo haber sido otro procedimiento o algoritmo principal.
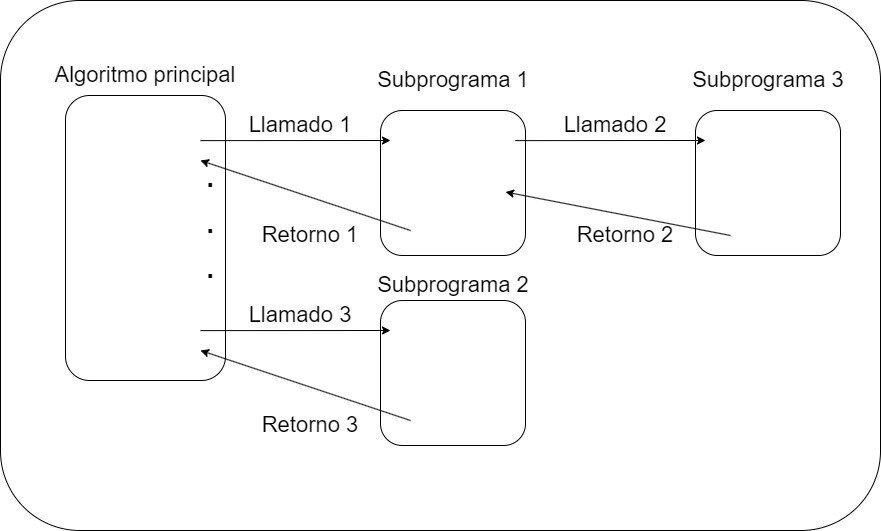
Esquema de llamados realizados por el algoritmo principal
Funciones y subrutinas
Para trabajar con procedimientos surgen los conceptos de funciones y subrutinas. Se debe tener presente que para trabajar con el esquema de procedimientos, se debe aplicar el lema "Divide y vencerás" al problema que se desee resolver.
Subrutinas
Este tipo de procedimiento se debe invocar desde el algoritmo principal o desde otro procedimiento. En ese instante cuando es llamado, se detendrá momentáneamente el programa que en ese instante se esté realizando y se cede el control a la subrutina invocada, la cual procederá a ejecutarse. Una vez ejecutada la subrutina, esta devuelve el control a quien la llamó y el algoritmo seguirá la ejecución que tenga establecida.
Subrutinas
SUBRUTINA<nombre_de_la_subrutina>(parámetro_1:tipo, parámetro_2:tipo,..., parámetro_n:tipo)
{lógica a ejecutar}
FIN-SUBRUTINALa declaración de una subrutina requiere de un conjunto de pasos que la definen, tal como sigue:
Invocación
EJECUTAR<nombre_de_la_subrutina>(parámetro_1:tipo, parámetro_2:tipo,..., parámetro_n:tipo)Puede ser llamada desde al algoritmo principal o dentro de otra subrutina o función. Se usará la palabra EJECUTAR para hacer el respectivo llamado y ejecución.
Declaración
Parámetros
La lista de parámetros formales en las declaraciones de las subrutinas pueden ser de 3 tipos: Entrada(E), Salida (S), Entrada-Salida (E/S).
Funciones
Existen 2 tipos de funciones:
- Funciones de librería: son funciones ofrecidas por el lenguaje en particular que se utilice, por tanto no requieren de una previa implementación, por ejemplo: sen(x), cos(x), len(x), int('2'), VAL("1234"), entre otros.
- Funciones implementadas por el programador: Procedimientos que el programador desarrolla para poder satisfacer alguna necesidad específica, tales como
- suma(a:entero,b:entero)
- mayorElementoVector(v:entero, n:entero)
- entre otros.
Funciones
FUNCIÓN <nombre_de_la_función>(parámetro_1:tipo, parámetro_2:tipo, ..., parámetro_n:tipo)
{lógica a ejecutar}
nombre_de_la_función <-- resultado_obtenido || retorna resultado_obtenido
FIN-FUNCIÓNLa declaración de una función también requiere de un conjunto de pasos que la definen, tal como sigue:
Invocación
Declaración
La ejecución de una función NO requiere de la palabra EJECUTAR, ya que esta instrucción está reservada solo para invocar subrutinas. Cuando se van a ejecutar funciones es necesario determinar con antelación qué se va a hacer con el resultado que se obtenga de la función. Suponga que existe una función suma, la cual calcula la suma entre dos valores a y b, y desea almacenar su suma en una variable c para un posterior análisis. Entonces tendríamos la siguiente instrucción:
C <-- suma(a,b)Funciones
La serie de parámetros en una función solo son de Entrada (E), lo que quiere decir que los parámetros de una función son de lectura y su contenido se debe conocer para poder ejecutarla.
También, en una función NO existen parámetros de entrada/salida (E/S) y solo debe existir un parámetro de salida, el cual será un dato, NO un conjunto de datos, y vendrá almacenado en el nombre de la función o como retorno.
Cabe mencionar que, para efectos del curso, si el resultado que desea es un conjunto de datos, como por ejemplo un vector o matriz, con funciones NO podrá realizarlo, sino estrictamente con con subrutinas.
Parámetros en funciones
Parámetros formales vs actuales
Los parámetros son utilizados en procedimientos, sin importar si es función o subrutina, estos pueden ser variables que representen un dato o arreglos, matrices o vectores que representen un conjunto de datos.
Cabe destacar que los parámetros y/o argumentos se les conoce de dos maneras:
- Formales: se ubican en la declaración de la subrutina o función
- Actuales: se colocan cuando se invoca la subrutina o función
Ejemplo:
- Parámetros formales:
- Parámetros actuales:
SUBRUTINA leerVector(v:entero, n:entero)
para (i <-- 1, n, 1)
leer v[i]
fin-para
FIN-SUBRUTINAEJECUTAR leerVector(a,10)
EJECUTAR leerVector(b,7)
EJECUTAR leerVector(b,9)Parámetros E, S, E/S
Recordemos que los parámetros pueden ser de 3 tipos, abordaremos ahora una explicación para cada caso:
- Entrada(E): Si el contenido de ellos se necesita conocer con antelación a la ejecución del procedimiento. Por ejemplo, si necesita realizar un procedimiento que escriba un vector, con lo que usted debe tener el vector alojado en una variable arreglo con su respectiva dimensión.
- Salida(S): Si el contenido de ellos solo se conoce después de la ejecución del procedimiento. Por ejemplo, si necesita realizar un procedimiento para leer un vector, este será leído solo dentro del procedimiento, ya que antes de que se ejecute los elementos del vector y su dimensión eran desconocidos.
- Entrada/Salida (E/S): Cuando el contenido de los parámetros, antes de ejecutar el procedimiento, varían con respecto a los valores que tiene después de que el mismo es ejecutado. Es decir, son parámetros cuyos valores son modificados en el transcurso del procedimiento. Ejemplo: eliminar elemento de un vector.
Tipos de variables
Comúnmente las variable pueden ser locales o globales. Con lo que surge el término alcance (scope).
- Locales: son variables que se declaran en el respectivo procedimiento que se emplea. Por lo que una misma variable puede ser declarada de distintas maneras en varios subalgoritmos. Ya que, una variable declarada en un procedimiento solo aparecerá en memoria principal al momento de ejecutarse el subalgoritmo donde se halle; con lo que, una vez que el mismo termine, la variable desaparecerá de la memoria principal.
- Globales: son variables que se declaran solo en el algoritmo principal, y permanecerá en memoria principal durante el transcurso de ejecución de todo el programa. Al tener una variable de este tipo, esta no se necesita pasar como parámetro para la ejecución de la subrutina o función, ya que a su contenido se puede acceder en cualquier instante.
Ventajas de variables
globales y locales
- Locales: su utilización hace que los procedimientos sean totalmente independientes del algoritmo principal.
- Globales: por medio de estas se puede compartir información entre procedimientos.
Es importante tener presente que el concepto de variables locales y globales solo existe a nivel de programación y no de algoritmos.
Ejemplo 1
Sean dos vectores a y b de tamaño n y m respectivamente. El vector a contiene los códigos de los estudiantes que perdieron algoritmia y programación 1 y el vector b el código de los estudiantes que perdieron Cálculo 1. Genere:
- Un vector con los estudiantes que perdieron ambas materias.
- Un vector con los estudiantes que perdieron al menos 1 materia.
Ejercicio
El Departamento de admisiones de la UN desea registrar la información de estudiantes de algunos colegios de la región caribe. Esto con el fin de determinar una posible admisión y saber la oferta en sus diversos programas de pregrado. Los datos almacenados son: (Se deben validar los datos antes de registrarlos)
| id | Primer Nombre | Segundo Nombre | Primer Apellido | Segundo Apellido | Correo | Estrato | Punta ICFES | Programa |
|---|
Una vez tomada la información a dichos estudiantes se desea conocer lo siguiente:
- Promedio global ICFES
- ¿Qué programa tiene mayor interés?
- ¿Qué promedio ICFES tienen los estudiantes por programa?
- ¿Qué programas ofertados tienen su promedio por encima del global?
- ¿Qué programas tienen menor interés?
Para proteger la identificación de cada estudiante se estipula la siguiente operación hash para codificar el respectivo id, donde s es la concatenación de todo un registro de cada estudiante.
- Lista de programas ofertados: https://www.uninorte.edu.co/carreras
- El nombre solo debe tener letras.
- Validar correo: ---@---
- Estrato: 0-6.
- Puntaje ICFES: 0-500.
Ejemplo 2
Sea una matriz A de nxn de números enteros, realice un algoritmo para ordenarla ascendentemente. Lea una matriz B de nxn realice la siguiente operación (A+B)A y (A-B)B
Ejemplo 3
Lea una matriz A de nxm. Halle:
- El mayor elemento de A.
- Halle su transpuesta.
- Un vector con todos los elementos impares.
- Un vector con todos los elementos que sean primos.
- Un vector con todos los elementos que sean perfectos
- Calcular
7. ¿Qué análisis tiene de ?
Ejemplo 4
Lea un vector de n elementos. Halle:
- El mayor elemento de v
- Invierta v sin arreglos auxiliares.
- Elimine de v todos los elementos iguales a un x leído, no se puede usar arreglos auxiliares.
Ejemplo 5
Dado un vector que contiene el primer Apellido de n usuario, realice un algoritmo para ordenarlo alfabéticamente de la A a la Z.
Ejemplo 6
Suponga que el Centro Médico de la Universidad del Norte gestiona el registro de los estudiantes de ciencia de la Salud y las notas que sacaron en las 5 asignaturas que por lo general deben ver a través de una matriz de String teniendo en cuenta el Código estudiantil, Nombre del estudiante, semestre en curso. La nota del semestre depende de las 5 asignaturas.
A continuación, se detallan la estructura que debe tener cada una de la información a almacenar:
- Código estudiantil: números enteros positivos de 8 cifras.
- Nombre del estudiante: genera dos columnas con Primer Apellido y Primer nombre, mínimo debe tener 4 caracteres c/u.
- Semestre en curso: Solo números enteros positivos de 2 cifras y no puede ser mayor que 12 .
- N1, N2, ... , N5: Solo números reales en la escala de 0.0 a 5.0 y la parte decimal solo podrá tener máximo 2 cifras. Sobre la nota definitiva suponga que cada una equivale al 20%.
Ilustración:
| Código estudiantil | Primer Apellido | Primer Nombre | Semestre en curso | N1 | N2 | N3 | N4 | N5 |
|---|---|---|---|---|---|---|---|---|
| "11111111" | "Gaitán" | "Jorge" | "10" | "0.8" | "1.5" | "3.45" | "2.54" | "2.86" |
| "22222222" | "Duque" | "Ivan" | "1" | "0.23" | "0.45" | "4.3" | "4.5" | "4.55" |
| "13142323" | "Petro" | "Gustavo" | "2" | "2.3" | "0.4" | "0.4" | "'2.5" | "5.0" |
- Realice un algoritmo para poder almacenar de forma correcta la información en la matriz.
- Ordene la matriz por orden alfabético teniendo en cuenta el Apellido del estudiante.
- Una vez ordenada con 2. Imprima el registro completo de los primeros 5 estudiantes.
- Determine por cada semestre los estudiantes con mejor desempeño.
- Calcule el promedio con base en la nota definitiva de cada semestre e indique qué estudiantes están por encima de dicho valor.
- Calcule el promedio global con base en la nota definitiva e indique qué estudiantes están por debajo de dicho valor.
Recursividad

Recursividad
La recursividad es un concepto manejado a nivel de procedimientos, esta manera de programación no es más que subalgoritmos dentro de los cuales existen llamados y/o invocaciones a sí mismos.
https://www.google.com/search?q=recursion
El uso de recursividad, nos permite resolver problemas que no se pueden resolver con estructuras repetitivas tradicionales tales como (Mientras que, Para, Hacer hasta). Es decir, la recursividad es útil cuando no se cuenta con una solución iterativa simple.

Recursividad
También, la recursividad se puede entender como una herramienta poderosa que se puede aplicar en aquellos problemas que requieren de mucho cálculo y, al mismo tiempo, es una alternativa que reemplaza las estructuras repetitivas.
Cabe mencionar que en la realización de procesos recursivos, es necesario tener en cuenta que debe existir un punto de retorno que permita la finalización del proceso.

Condiciones para generar algoritmos recursivos.
Para que un algoritmo recursivo sea correcto, este debe generar una secuencia finita de llamados a sí mismo. Es por ello, que las condiciones que mencionarán deben analizarse detalladamente y verificar su funcionalidad en el desarrollo de estos algoritmos; estas condiciones las llamaremos el método de las 2 preguntas.
Método de las 2 preguntas
- La pregunta CASO-BASE: Hay una salida NO recursiva del procedimiento y debe funcionar para el mismo.
2. La pregunta LLAMADO MÁS PEQUEÑO: cada llamada recursiva al procedimiento se refiere a un caso más pequeño del problema original.


Inducción y Recursión
El principio de inducción matemática indica que, si un número entero posee cierta propiedad , y a su vez se puede demostrar que un número también la posee, esto implica que la tiene, entonces todos los números desde tienen la propiedad P (efecto dominó)
- Caso base:
- Caso inductivo:
Inducción y Recursión
Notemos que el en razonamiento recursivo, se confía que un problema puede ser resuelto a partir de resolver el mismo problema de una instancia previa.
Por lo que se puede tener una analogía entre el caso inductivo y la recursión. Sin embargo, se tendría que considerar que se debe resolver el problema no buscando una instancia siguiente, sino una instancia previa. Es decir no hacia x+1, sino hacia el x-1.
Se comprueba entonces que la instancia x-1 < x eventualmente será trivial de resolver. Por lo que el caso base resolverá la sumatoria para x=1 que será 1.
Inducción y Recursión
Finalmente resolvamos por recursión:
Tendríamos que pensar entonces en:
- Caso base:
- Llamados recursivos más pequeños:
Tipos de recursividad
- Cantidad de referencias
1. Recursividad simple.
2. Recursividad múltiple.
- Dirección
1. Recursividad directa.
2. Recursividad indirecta.
- Visibilidad
1. Recursividad explícita.
2. Recursividad implícita
Tipos de recursividad
- Cantidad de referencias
1. Recursividad simple: Solo hay una referencia recursiva
2. Recursividad múltiple: Hay más de una referencia recursiva. Si la función respeta el concepto de transparencia referencial, podemos usar memoization.
FUNCION sumatoria(n)
SI n = 1
RETORNA 1
SINO
RETORNA sumatoria(n-1) + n
FIN-SI
FIN-FUNCIONFUNCION fibonacci(n)
SI n = 0
RETORNA 0
SINO
SI n = 1
RETORNA 1
SINO
RETORNA fibonacci(n-1) + fibonacci(n-2)
FIN-SI
FIN-SI
FIN-FUNCIONTipos de recursividad
- Dirección
1. Recursividad directa: Hay referencia a sí mismo dentro su bloque o estructura
2. Recursividad indirecta: la referencia así mismo se realiza mediante intercambios. Es compleja de visualizar.
public class Nodo{
int dato;
Nodo link;
public Nodo(int dato){
this.dato = dato;
this.link = null;
}
}P1
P2
P3
Tipos de recursividad
- Dirección
- Recursión mutua: caso particular de recursión directa
FUNCION isEven(n)
SI n = 0
RETORNA true
SINO
RETORNA isOdd(n-1)
FIN-SI
FIN-FUNCIONFUNCION isOdd(n)
SI n = 0
RETORNA false
SINO
RETORNA isEven(n-1)
FIN-SI
FIN-FUNCIONTipos de recursividad
- Visibilidad
- Recursión explícita: es claro el llamado recursivo que se ejecutará en su propio bloque o estructura.
- Recursión implícita: No es claro el llamado recursivo, sino que
se muestra implícitamente en algún segmento invocado o
un elemento que lo compone.
SUB validarPrimo(n)
SI esPrimo(n)
ESC(n," es primo")
SINO
ESC(n, " no es primo")
FIN-SI
FIN-SUBRecursividad
Es importante mencionar que existen 2 formas de ir direccionando las ejecuciones recursivas realizadas. Estas son:
- Recursividad por pila
- Recursividad por cola
Para efectos prácticos, comenzaremos con la recursividad teniendo en cuenta una pila o en inglés "stack" la cual maneja el concepto LIFO.
Más adelante estaremos ilustrando la diferencia y cómo podemos mejorar los algoritmos realizados mediante la recursión por cola.
Estructura recursiva básica
Números naturales
¿Cómo podemos formar el conjunto de números naturales recursivamente?
Pensemos en el elemento base: 0
Notemos que podemos generar el siguiente al 0 sumando 1, 0+1=1
Para generar el siguiente debemos sumar 1 al 1: 1+1 = 2
Por lo que podemos notar que es necesario una función siguiente al n en donde se encuentre.
Factorial de un número
Caso base:
Llamado más pequeño:
Potencia de un número natural con exponente natural
Caso base:
Llamado más pequeño:
Lectura de un vector de forma recursiva
| 34 | 565 | 453 | 13 | 4 | 892 | 88 | 86 | 23 | 3 |
|---|
a
1 2 3 4 5 6 7 8 9 10
i
Caso base:
Llamado más pequeño:
Generar vector de forma recursiva que contenga la sucesión de Fibonacci
Caso base:
Llamado más pequeño:
Búsqueda en un vector de forma recursiva
| 34 | 565 | 453 | 13 | 4 | 892 | 88 | 86 | 23 | 3 |
|---|
a
1 2 3 4 5 6 7 8 9 10
i
Caso base:
Llamado más pequeño:
Lectura de una matriz de forma recursiva
Caso base:
Llamado más pequeño:
Ejercicio
Caso base:
Llamado más pequeño:
De manera recursiva, lea 2 matrices A y B de tamaño nxm. Calcule e imprima de igual manera lo siguiente:
1. (A+B)
2. (A-B)
3.
4.
Multiplicación Egipcia
Caso base:
Llamado más pequeño:
Coeficiente Binomial
Caso base:
Llamado más pequeño:
Generar vector de primos desde una matriz de forma recursiva
Caso base:
Llamado más pequeño:
| 2 | 3 | 11 |
a=
1 2 3
i
Generar caracol de forma recursiva
Caso base:
Llamado más pequeño:
Módulo de un número
Caso base:
Llamado más pequeño:
5%3 = 2
Algoritmo de Euclides
Ejercicio práctico
Utilizando procedimientos recursivos, lea 3 matrices A, B y C de tamaño nA x mA, nB x mB, y nC x mC, respectivamente. Halle:
- La sumatoria de los elementos de la triangular inferior de la matriz A sin incluir su diagonal principal.
- La sumatoria de los elementos de la triangular superior de la matriz B sin incluir su diagonal principal.
- D = (A+B)C, si la sumatoria de 1. es mayor que la de 2.
- D = A - ((B)(C)), si la sumatoria de 1. es menor que la de 2.
- D = (A+B)(B-C), si la sumatoria de 1. es igual a la de 2.
Método Quicksort
Este algoritmo es una de las aplicaciones más importantes en términos de recursividad. Ya que en la actualidad se le conoce como el método de ordenamiento óptimo en términos tiempo de ejecución. Sin embargo existen otras técnicas como TimSort. Ya que el método de quicksort puede ser inestable para casos específicos.
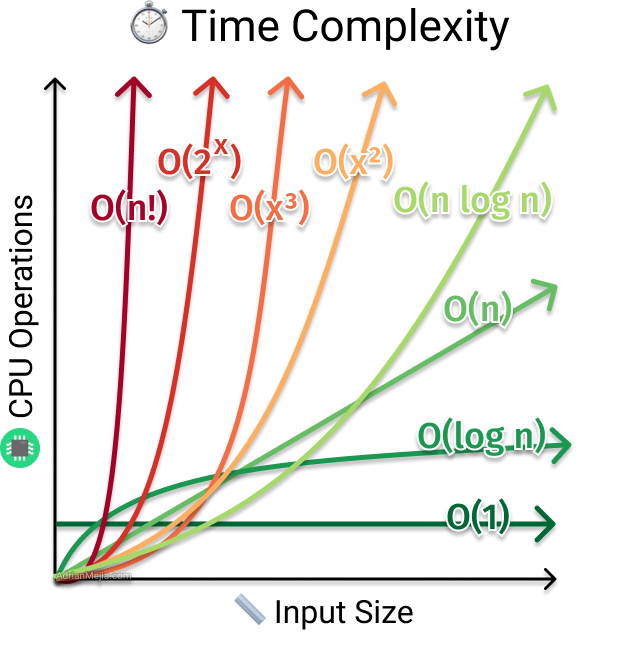
Implementación Quicksort
Recursión de pila vs cola
- Pila en la recursión
- Recursión de cola
- Eliminación de recursión
- Conversión con acumulador
- Recursión con pila explícita
Recursión Gráfica
Fractales


Algoritmia y Programación II
By Sebastian Ariza
Algoritmia y Programación II
- 993



