Estructura de datos II

M.Sc. Sebastian David Ariza Coll

Árboles

Generalidades.
Árboles binarios de búsqueda - ABB (SBT).
Árboles AVL - Adelson-Velskii y Landis.
Árboles B.

Siguiente tema

Generalidades

Definición
- Árboles binarios.
- Representación.
- Elementos principales.
Recorridos
- Pre-Order traversal
- In-Order traversal
- Post-Order traversal
- Level-Order traversal

Recorridos

SUB preOrderT(Node node)
|	if(node != null)
|	|	ESC(node.data)
|	|	EJECUTAR inOrderT(node.izq)
|	|	EJECUTAR inOrderT(node.der)
|	end-if
end-function

SUB inOrderT(Node node)
|	if(node != null)
|	|	EJECUTAR inOrderT(node.izq)+
|	|	ESC(node.data)
|	|	EJECUTAR inOrderT(node.der)
|	end-if
end-function

SUB postOrderT(Node node)
|	if(node != null)
|	|	EJECUTAR inOrderT(node.izq)
|	|	EJECUTAR inOrderT(node.der)
|	|	ESC(node.data)
|	end-if
end-function

Reconstruir un árbol binario

Dado el Pre-Order traversal y el In-Order traversal reconstruya el árbol binario.

Pre-Order traversal: "A", "B", "D", "E", "C", "F"
In-Order traversal: "D", "B", "E", "A", "F", "C"

Árboles ABB

Propiedades
Operaciones básicas:
- Búsqueda.
- Inserción.
- Eliminación.

Propiedades - ABB

Son árboles de grado 2 - Binarios.
Cada nodo puede tener 0, 1 o 2 hijos.
A los hijos le llamaremos hijo izquierdo o hijo derecho.

Para almacenar la información se tienen en cuenta 3 criterios:
- Todos los hijos izquierdos son menores a su nodo padre.
- Todos los hijos derechos son mayores a su nodo padre.
- Los valores en cada nodo son únicos.

Apuntador hijo izquierdo

Apuntador hijo derecho

Búsqueda - ABB

Tener presente:
1. Todos los valores menores están a la izquierda de cada nodo padre.
2. Todos los valores mayores están a la derecha de cada nodo padre.
Pasos a seguir:
- Casos bases:
  1. No se encontró el elemento.
  2. El valor a buscar es igual al nodo donde se encuentra.
- Llamados recursivos: Al comparar el nodo actual con el elemento:
  1. Si es mayor, moverse hacia su hijo izquierdo, el elemento es menor que su padre.
  2. Si es menor, moverse hacia su hijo derecho, el elemento es mayor que su padre.

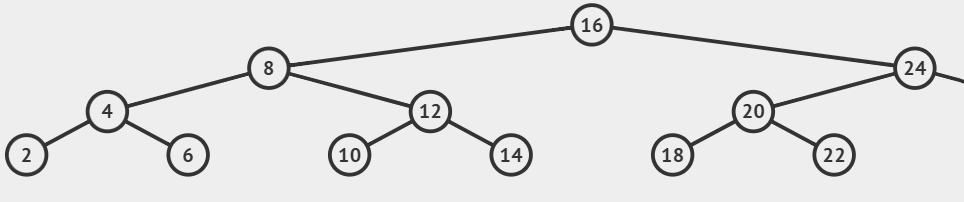
Búsqueda - ABB

function searchABBR(Node node, Ent: x)
|	//Casos bases --> Llamados NO recursivos
|	if(node = null) // Se ha recorrido todo el árbol y no se ha encontrado.
|	|	return null
|	end-if
|   if(node.data == x)//Se ha encontrado el elemento
|	|	return node
|	end-if
|	
|	//LLamados recursivos
|	if(node.data > x)// El dato a buscar es menor que el padre, avanzar hacia la izq
|	|	return searchABBR(node.izq, x)
|	end-if
|	if(node.data < x)// El dato a buscar es mayor que el padre, avanzar hacia la der
|	|	return searchABBR(node.der, x)
|	end-if
end-function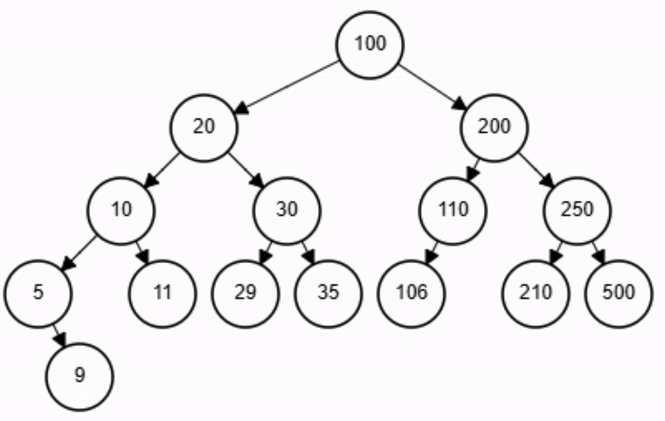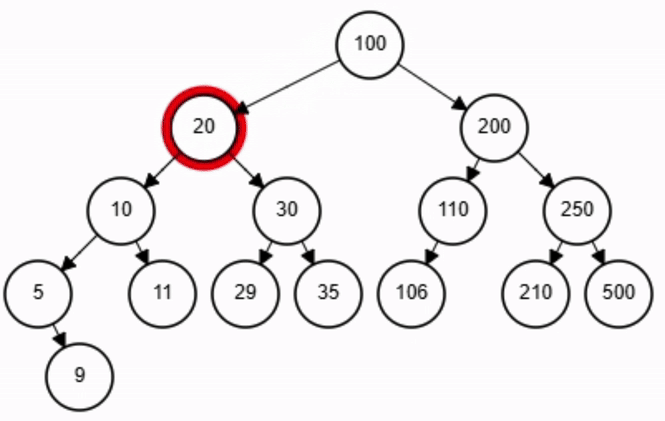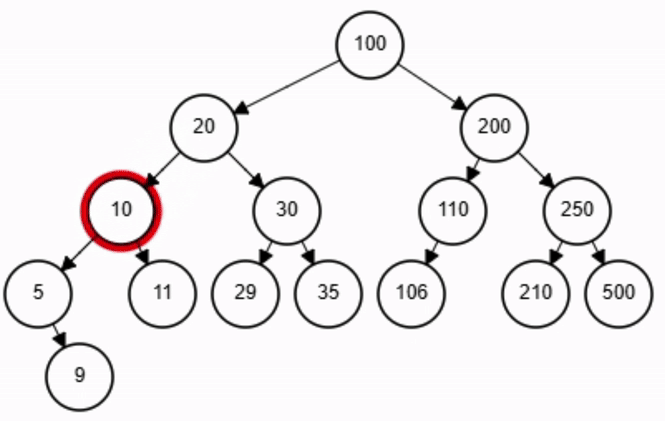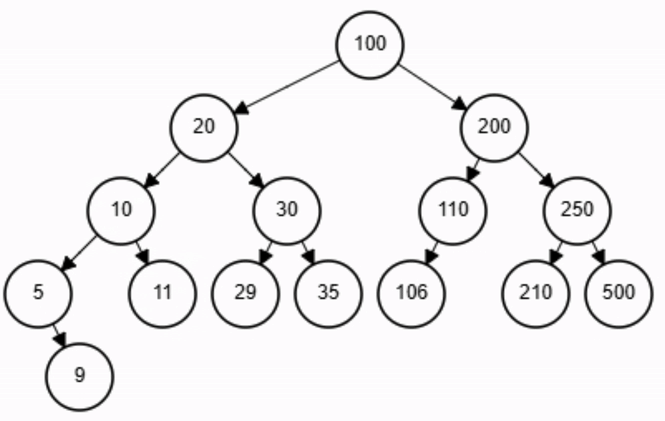

x = 11

Inserción - ABB

Tener presente:
1. Todos los valores menores están a la izquierda de cada nodo padre.
2. Todos los valores mayores están a la derecha de cada nodo padre.
Pasos a seguir:
- Casos bases:
  1. No se encontró el elemento.
  2. El valor a buscar es igual al nodo donde se encuentra.
- Llamados recursivos: Al comparar el nodo actual con el elemento:
  1. Si es mayor, moverse hacia su hijo izquierdo, el elemento es menor que su padre.
  2. Si es menor, moverse hacia su hijo derecho, el elemento es mayor que su padre.

Inserción - ABB

function addNode(Node node, Ent: data)
|	//Casos bases --> Llamados NO recursivos
|	if(node = null) // Se ha encontrado el padre del nuevo nodo
|	|	return getNode(x)
|	end-if
|	if(node.data == data) // Se ha encontrado el padre del nuevo nodo
|	|	ESC(x," ya existe dentro del árbol.")
|	end-if
|	//LLamados recursivos
|	if(node.data > data)// El dato a añadir es hijo izq
|	|	node.izq <-- addNode(node.izq, data)
|	end-if
|	if(node.data < data)// El dato a añadir es hijo der
|	|	 node.der <-- addNode(node.der, data)
|	end-if
|	return node
end-function

data = 11

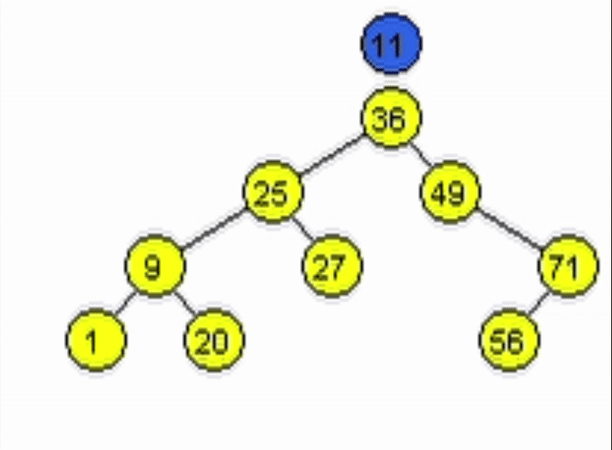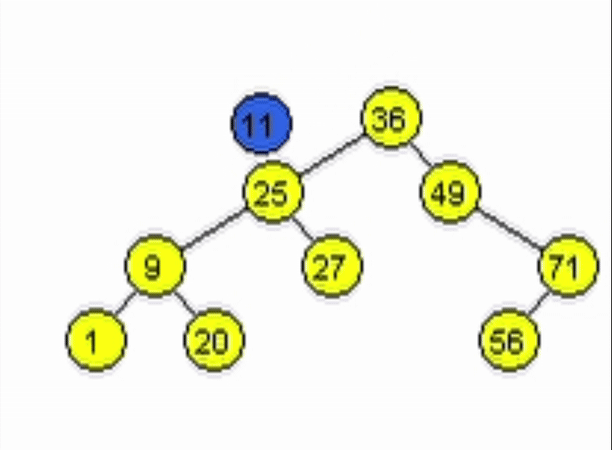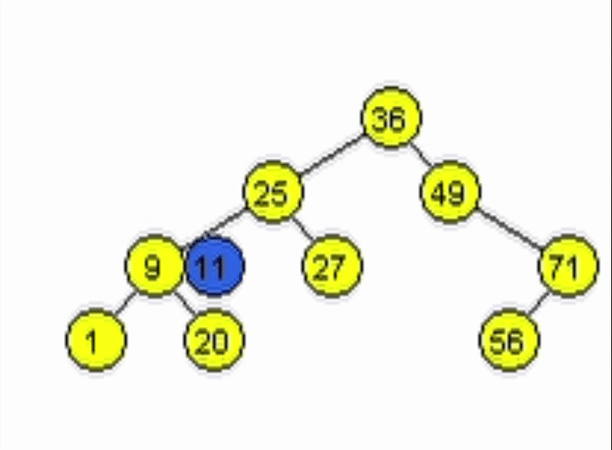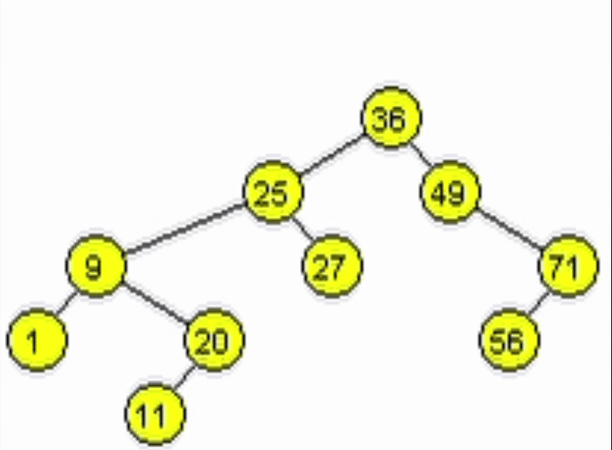
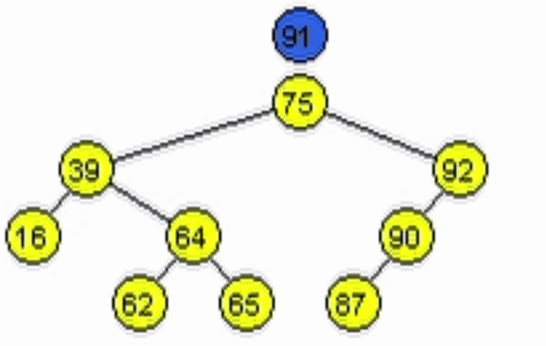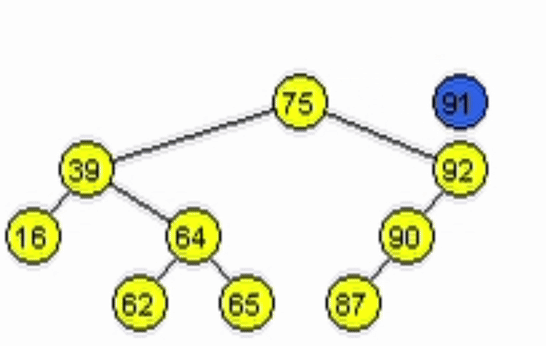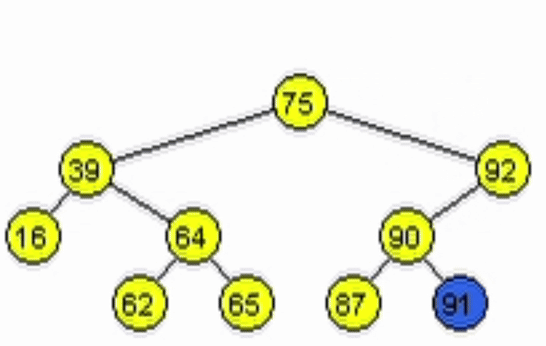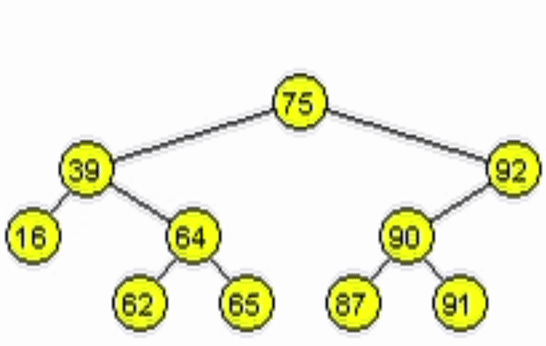
data = 91

Eliminación - ABB

Dada la naturaleza de un ABB, para eliminar un nodo se deben contemplar 3 casos:

El nodo a eliminar es un nodo hoja.
El nodo a eliminar tiene 1 único hijo (Izquierdo o Derecho).
El nodo a eliminar tiene exactamente 2 hijos.

Como en la inserción, cada vez que se avanza se va van haciendo los llamados a izquierda o derecha sobre cada nodo. Esto con el fin de hacer las modificaciones en los enlaces de los nodos según el caso que aplique.

Eliminación - ABB

Caso 1. Nodo hoja.

Se debe indicar al padre del nodo a eliminar que apunte a nulo.
El nodo hoja puede ser hijo izquierdo o derecho. Sin embargo, sus dos hijos apuntan a nulo.

function deleteR(Node node, Ent: data)
|	//Casos bases --> Llamados NO recursivos
|	if(node == null) // No se ha encontrado el elemento
|	|	return null
|	end-if
|	if(node.data == data)
|   |	if(node.izq = null) 
|   |	|	return node.der
|   |	end-if
|	end-if
|	//LLamados recursivos
|	if(node.data > data) // El dato a añadir es hijo izq
|	|	node.izq <-- deleteR(node.izq, data)
|	end-if
|	if(node.data < data)// El dato a añadir es hijo der
|	|	 node.der <-- deleteR(node.der, data)
|	end-if
|	return node
end-function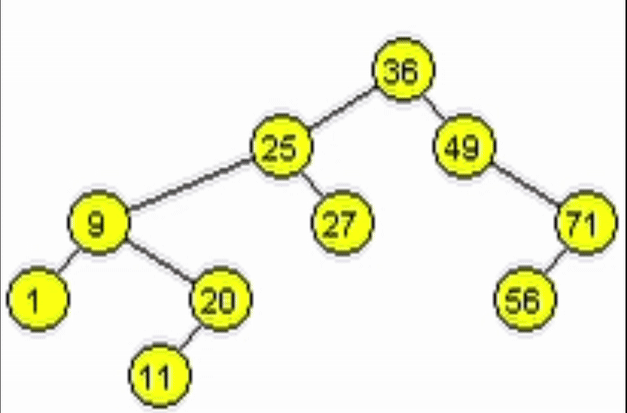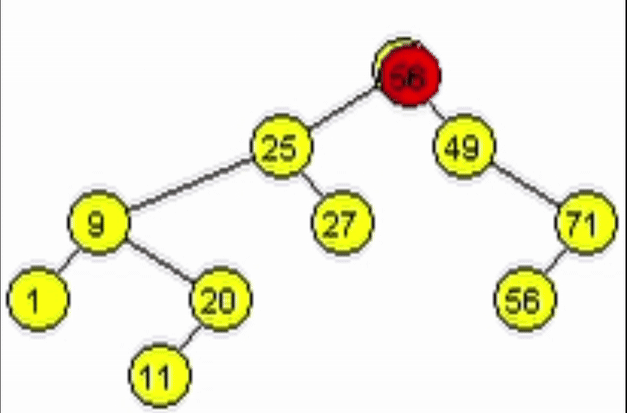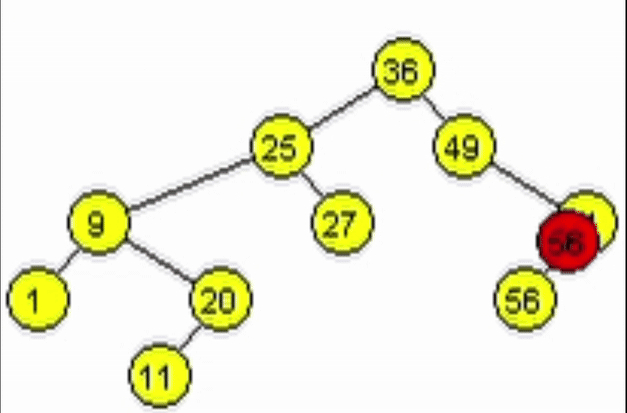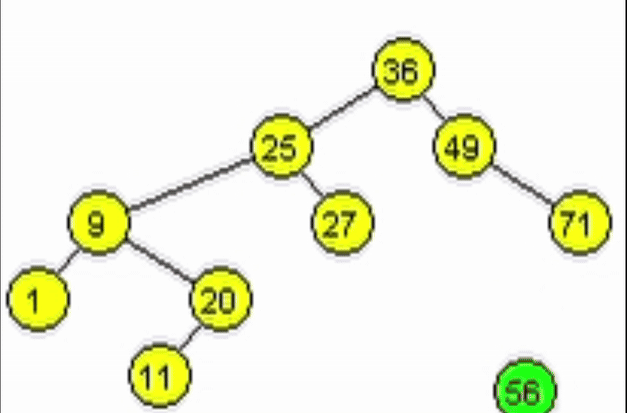

Eliminación - ABB

Caso 2. Tiene un único hijo.

Al tener 1 hijo, puede estar a izquierde o derecha.
- Si está a derecha se debe retornar el hijo derecho.
- Si está a izquierda se debe retornar el hijo izquierdo.

function deleteR(Node node, Ent: data)
|	//Casos bases --> Llamados NO recursivos
|	if(node == null) // No se ha encontrado el elemento
|	|	return null
|	end-if
|	if(node.data == data)
|   |	if(node.izq = null) 
|   |	|	return node.der
|   |	end-if
|   |	if(node.der = null) 
|   |	|	return node.izq
|   |	end-if
|	end-if
|	//LLamados recursivos
|	if(node.data > data) // El dato a añadir es hijo izq
|	|	node.izq <-- deleteR(node.izq, data)
|	end-if
|	if(node.data < data)// El dato a añadir es hijo der
|	|	 node.der <-- deleteR(node.der, data)
|	end-if
|	return node
end-function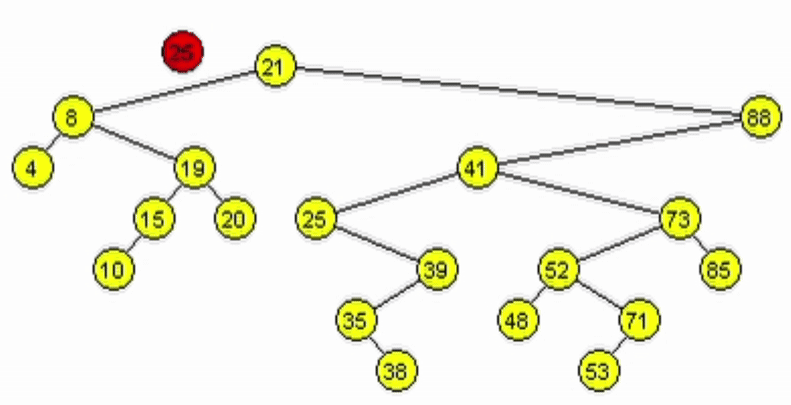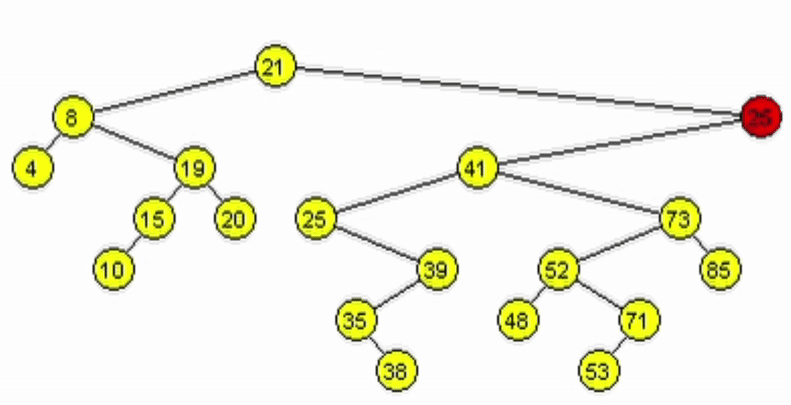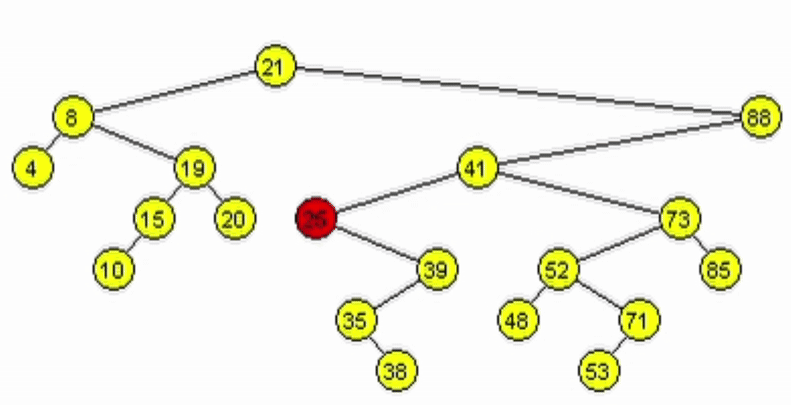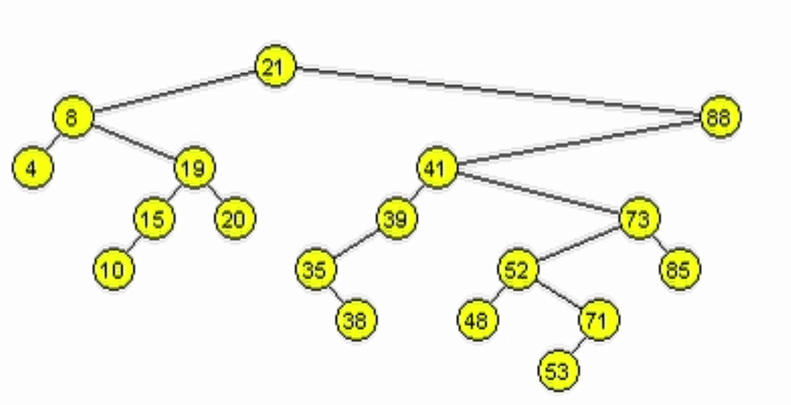

Eliminación - ABB

Caso 3: El nodo a eliminar tiene 2 hijos.

Se debe mantener la estructura ABB. Tomar 1 de las 2 opciones:
1. Predecesor: es el nodo mayor de los menores del subárbol izquierdo del nodo a eliminar.
2. Sucesor: es el nodo menor de los mayores del subárbol derecho del nodo a eliminar.
Reescribir la información del nodo a eliminar con la del nodo encontrado.
Eliminar el nodo tomado como sucesor o predecesor.

function deleteR(Node node, Ent: data)
|	//Casos bases --> Llamados NO recursivos
|	if(node == null) // No se ha encontrado el elemento
|	|	return null
|	end-if
|	if(node.data == data)
|   |	if(node.izq = null) 
|   |	|	return node.der
|   |	end-if
|   |	if(node.der = null) 
|   |	|	return node.izq
|   |	end-if
|	|	Node sucesor <-- minSubDer(node.der)
|	|	node.data <-- sucesor.data
|	|	node.der <-- deleteR(node.der, sucesor.data)
|	end-if
|	//LLamados recursivos
|	if(node.data > data) // El dato a añadir es hijo izq
|	|	node.izq <-- deleteR(node.izq, x)
|	end-if
|	if(node.data < data)// El dato a añadir es hijo der
|	|	 node.der <-- deleteR(node.der, x)
|	end-if
|	return node
end-function

function minSubDer(Node node)
|	if(node.izq != null)
|	|	return minSubDer(node.izq)
|	end-if
|	return node
end-function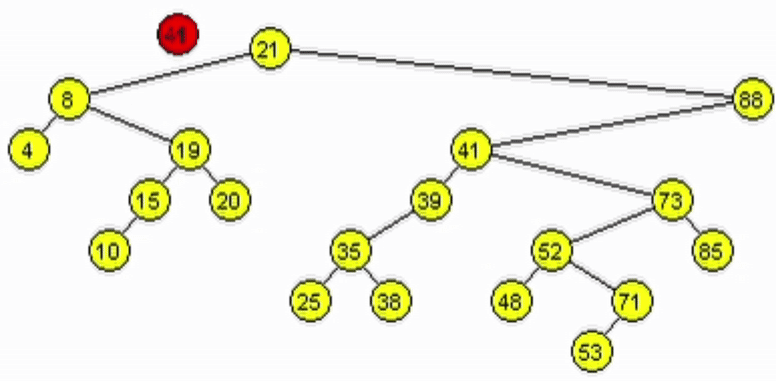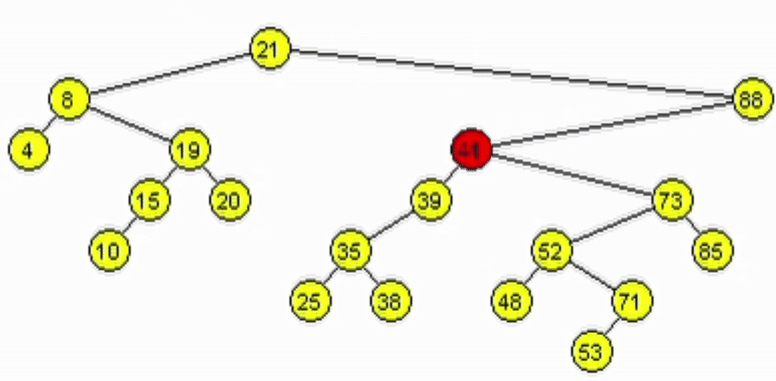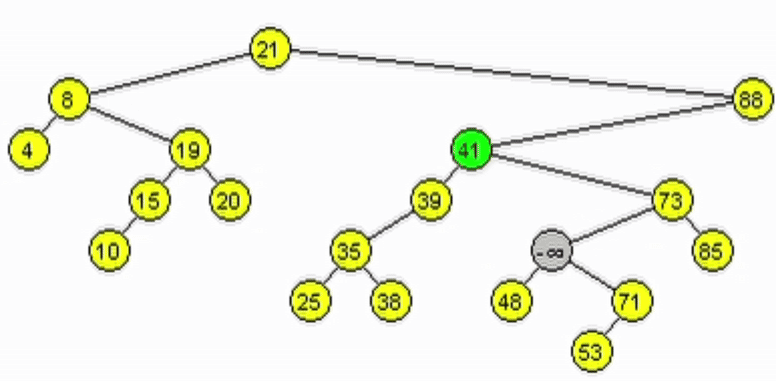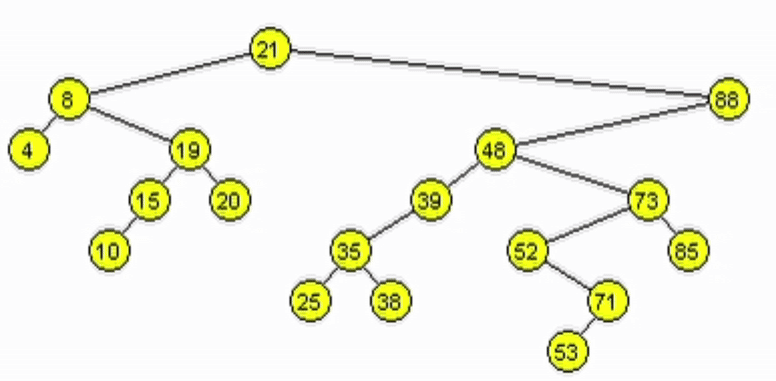

Altura de un árbol binario

Longitud del camino más largo desde la raíz hasta una hoja.

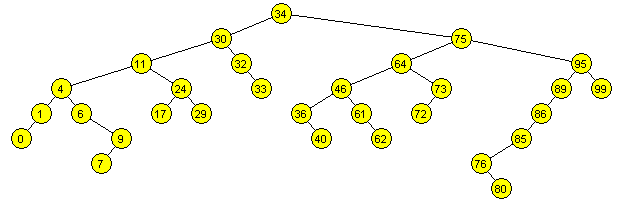
¿Cuántos elementos hay en un árbol binario?

Árbol binario lleno

Cada nodo o es una hoja o tine grado igual a 2

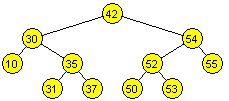
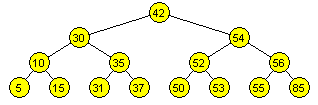
Árbol binario completo

Todos los nodos excepto los del último nivel, tienen dos hijos

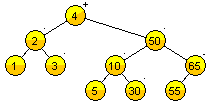
Árboles AVL

Creados por: Adelson-Velskii y Landis. en 1962.
Mitigan el crecimiento o decrecimiento descontrolado en los ABB.
La altura del árbol es esencial, y se busca minimizar.
La diferencia entre las alturas de los subárboles izquierdo y derecho de cualquier nodo no puede ser mayor que 1.
Mejora de complejidad temporal de la búsqueda, inserción, eliminación, máximo y mínimo a . Ya que la altura en un AVL está limitada por .
Las restricciones estructurales buscan que la altura tienda a escala logarítmica.

\mathcal{O}(\log n)

Árboles AVL

Definimos formalmente a un árbol AVL, como un árbol ABB, donde la diferencia entre las alturas de los subárboles izquierdo y derecho de cualquier nodo NO puede ser mayor que 1.

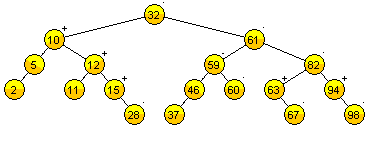
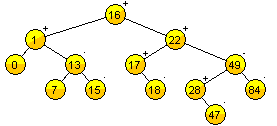
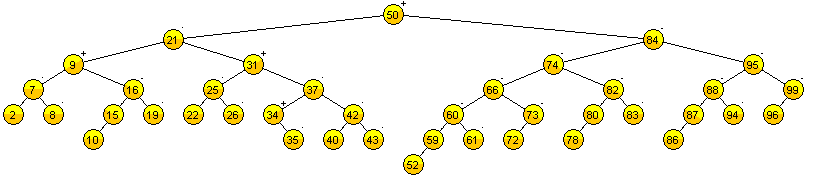
A la diferencia entre la altura del subárbol izquierdo y derecho de cualquier nodo la nombraremos como factor de equilibrio.

node.balance = height(node.left) - height(node.right)

Note que el factor de equilibrio de cada nodo en un AVL puede dar como resultado: -1, 0 o 1. Es decir

balance \in [-1,1]

Factor de equilibrio

Solo en la inserción o eliminación de un nodo, los nodos ascendientes (padres) del nodo pueden sufrir un cambio en su factor de equilibrio.

Si se produce un cambio, será solo en una unidad. Por tanto
- SI EL FACTOR DE EQUILIBRIO DE CUALQUIER NODO DA -2 O 2. SE ENTENDERÁ QUE EL NODO ESTÁ DESEQUILIBRADO Y POR ENDE EL ÁRBOL TAMBIÉN.

¡Tener presente!

Para reequilibrar el nodo, se deben utilizar ciertas operaciones llamadas rotaciones.

Operaciones

Búsqueda: Al ser un tipo de ABB, las operaciones de búsqueda se mantienen.
Eliminar o insertar: estas operaciones se realizan igual que las de un ABB. Sin embargo, surgirá un cambio en una unidad sobre los nodos padres del nodo. Por lo cual, se añade una etapa posterior de reequilibrio.
Reequilibrio
1. Se recorren los padres del nodo que ha sufrido modificación (enlaces).
2. Recalcular los factores de equilibrio
3. Aplicar rotaciones según apliquen.
4. El recorrido se termina una vez se ha llegado a la raíz o cuando el subárbol del nodo actual no haya sufrido cambios en altura respecto a la situación anterior a la operación.

Rotaciones

Reestructuración de los enlaces de un subárbol manteniendo la propiedad de ordenamiento.
Pueden reestablecer el equilibrio del nodo (No importa que el nivel del árbol cambie).
Tipos de rotaciones:
- Rotación simple izquierda.
- Rotación simple derecha.
- Rotación doble derecha - izquierda.
- Rotación doble izquierda - derecha.

Rotaciones

Rotación simple izquierda.

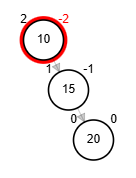
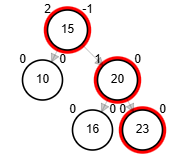
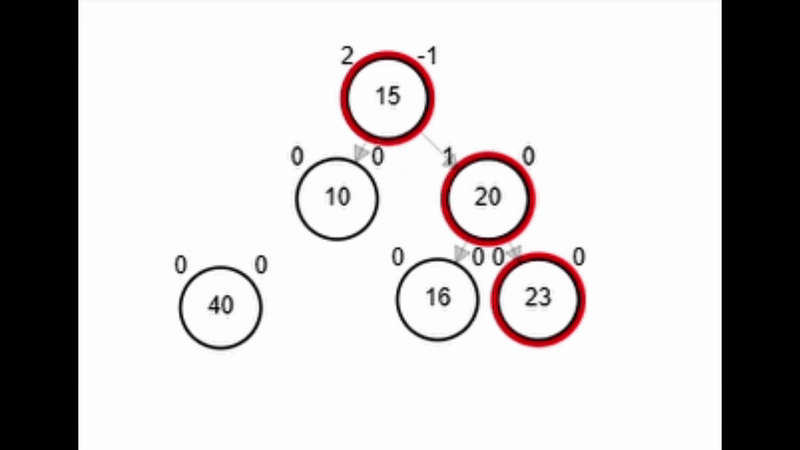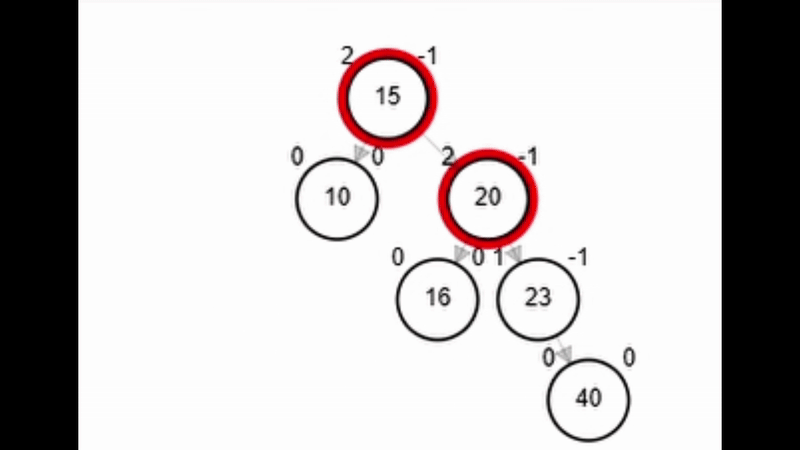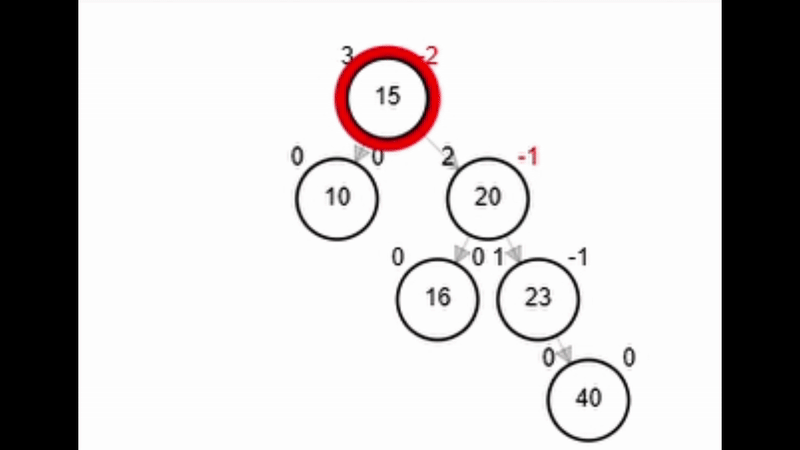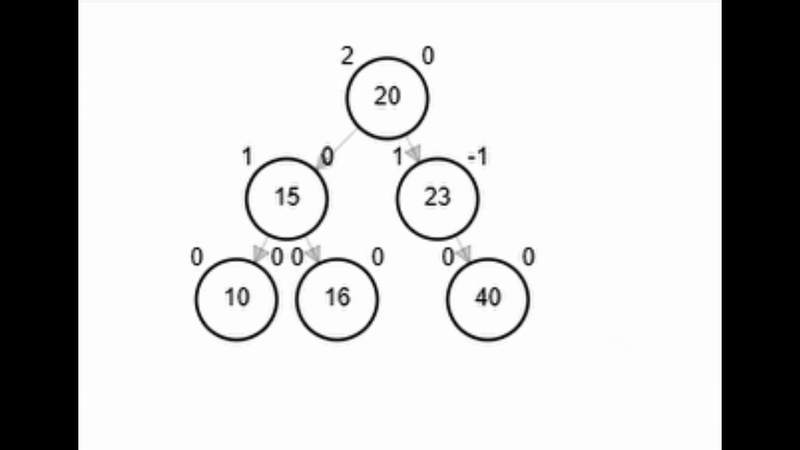
Rotaciones

Rotación simple izquierda.

function rSI(Node node)
|	Node aux <-- node.der
|	node.der <-- aux.izq
|	aux.izq <-- node
|	node.balance <-- fb(node)
|	aux.balance <-- fb(aux)
|	return aux
end-function

Add 40

Rotaciones

Rotación simple derecha.

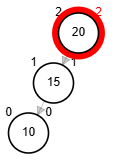
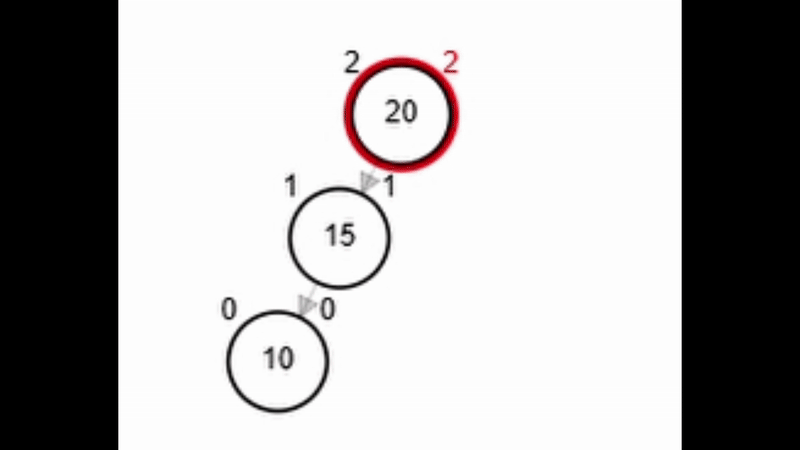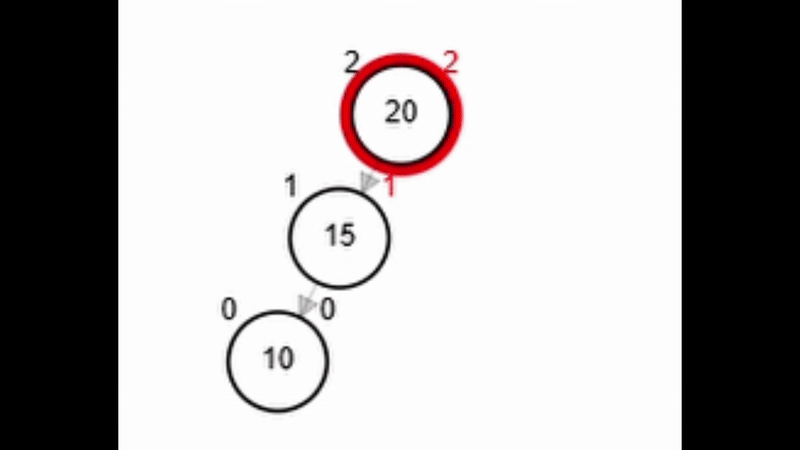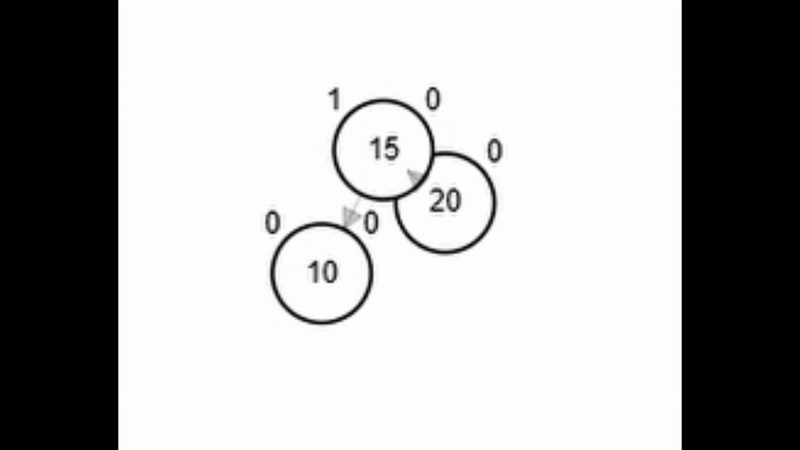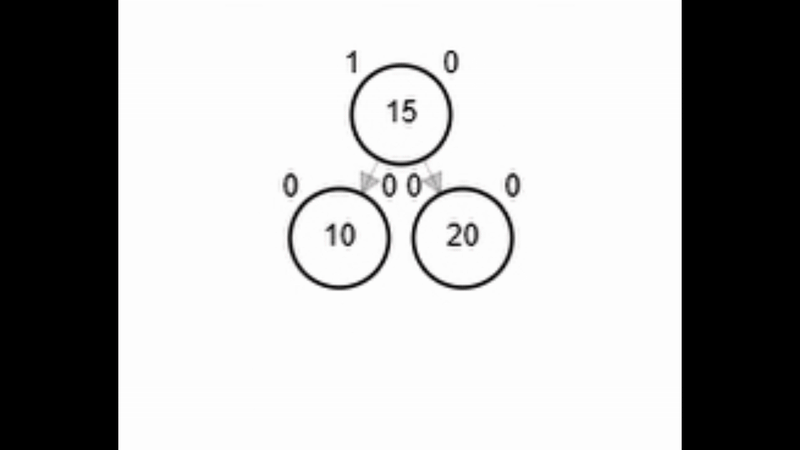
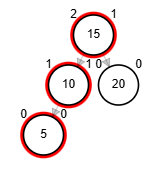
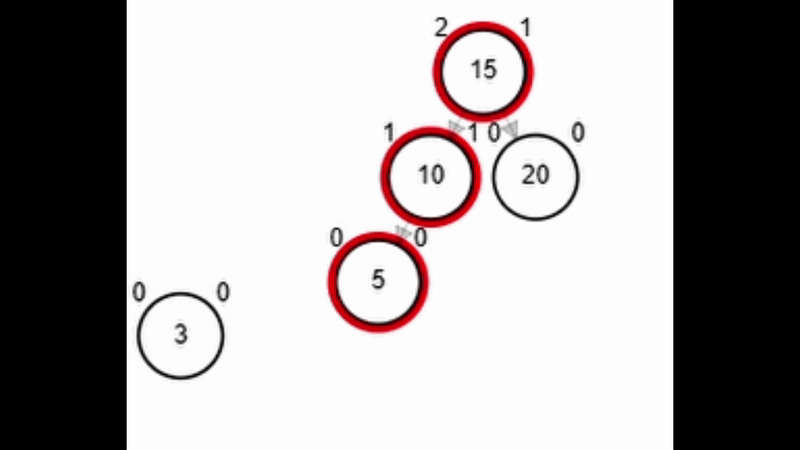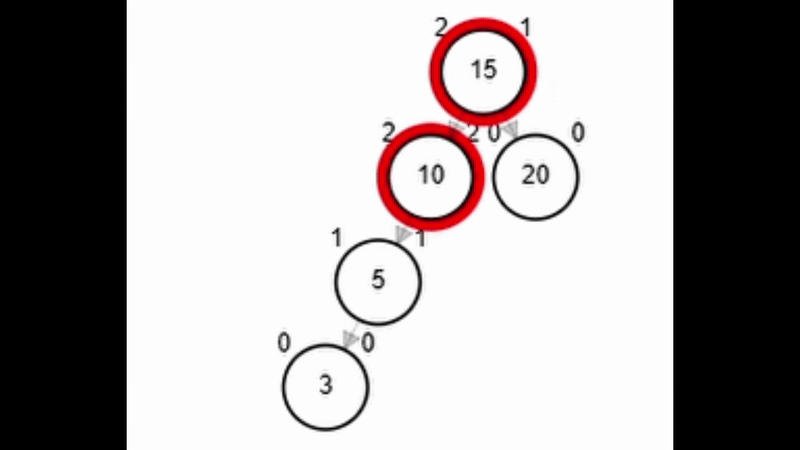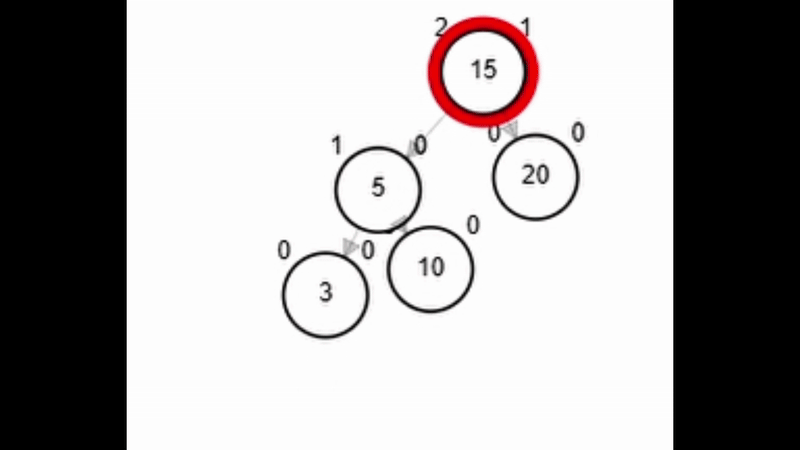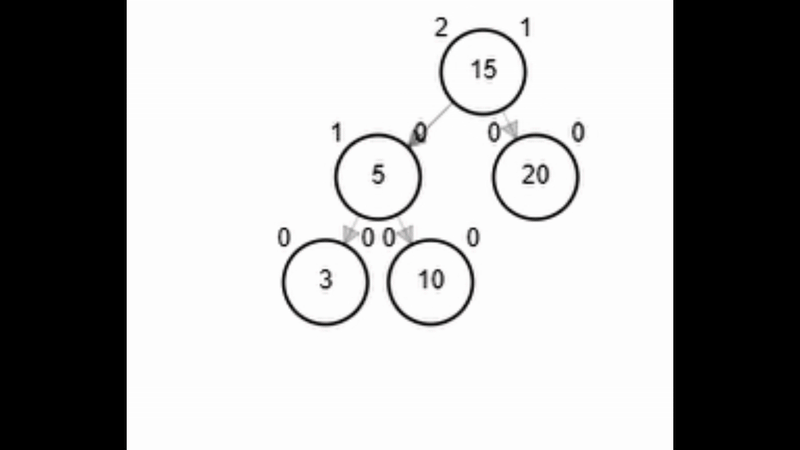
Add 3

Rotaciones

Rotación simple derecha.

function rSD(Node node)
|	Node aux <-- node.izq
|	node.izq <-- aux.der
|	aux.der <-- node
|	node.balance <-- fb(node)
|	aux.balance <-- fb(aux)
|	return aux
end-function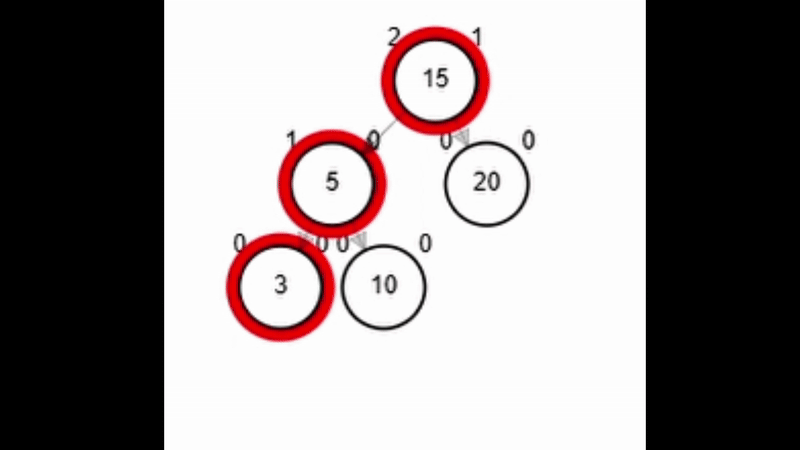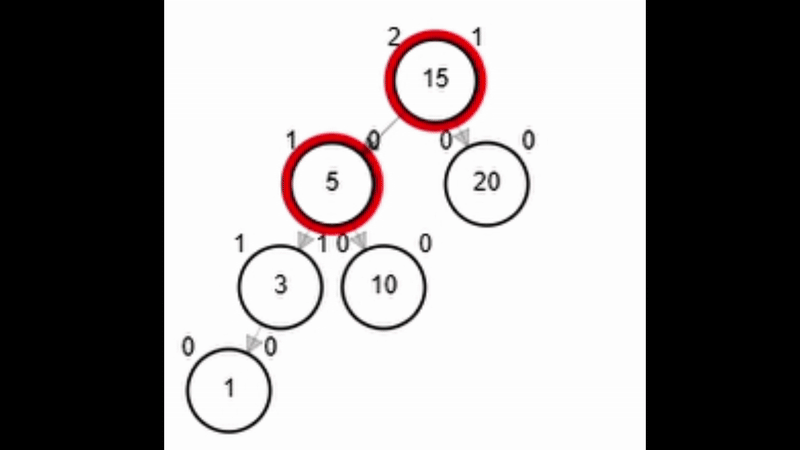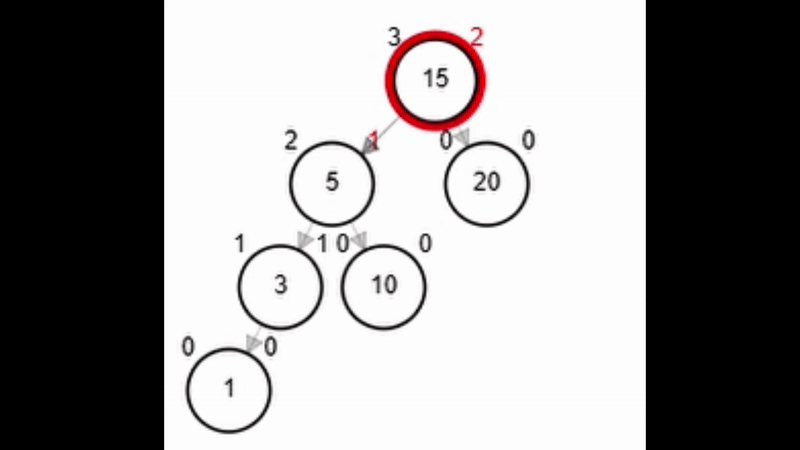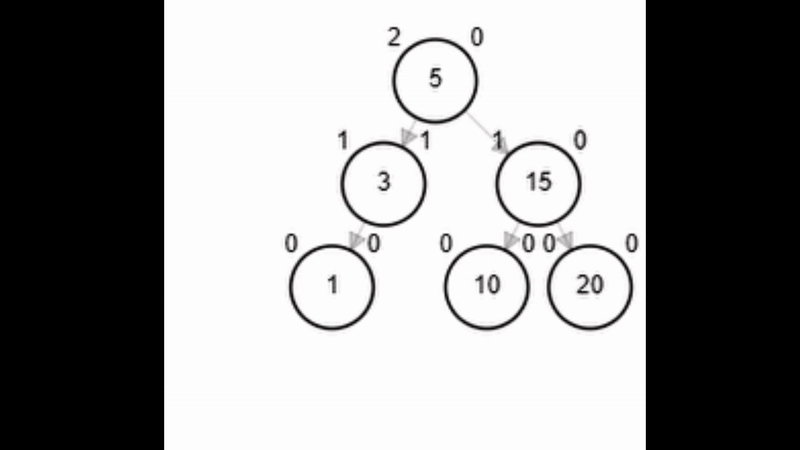

Add 1

Rotaciones

Rotación doble: izquierda derecha.

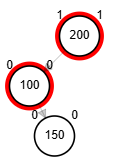
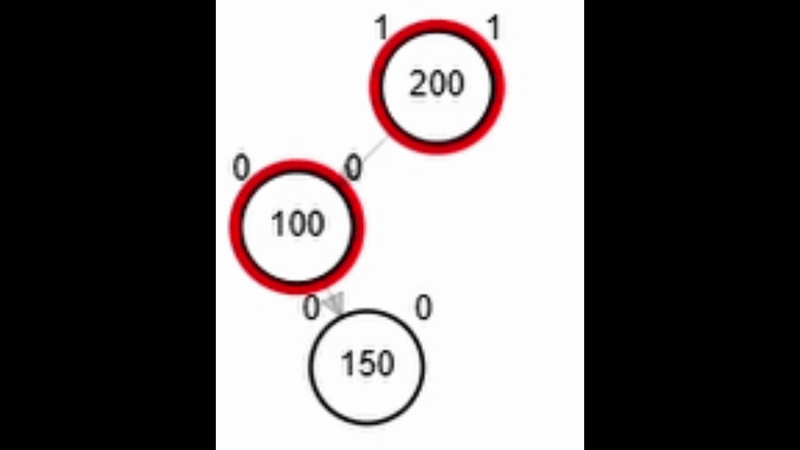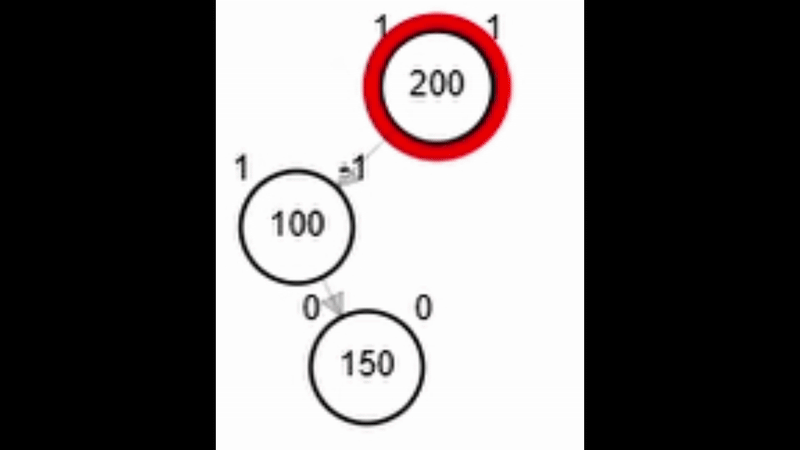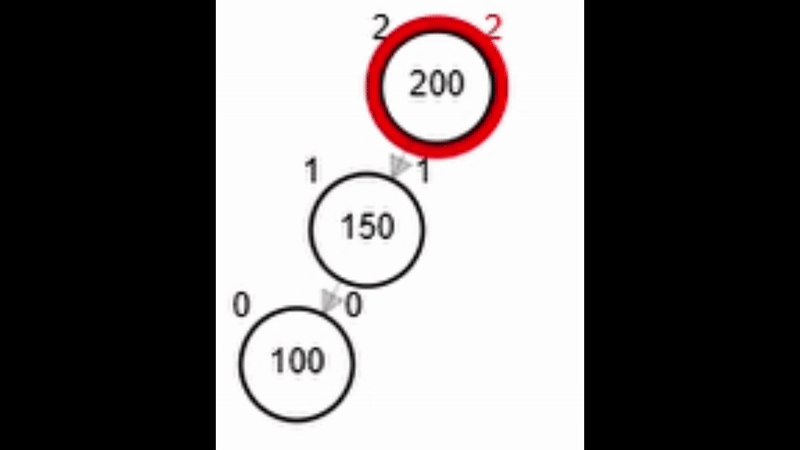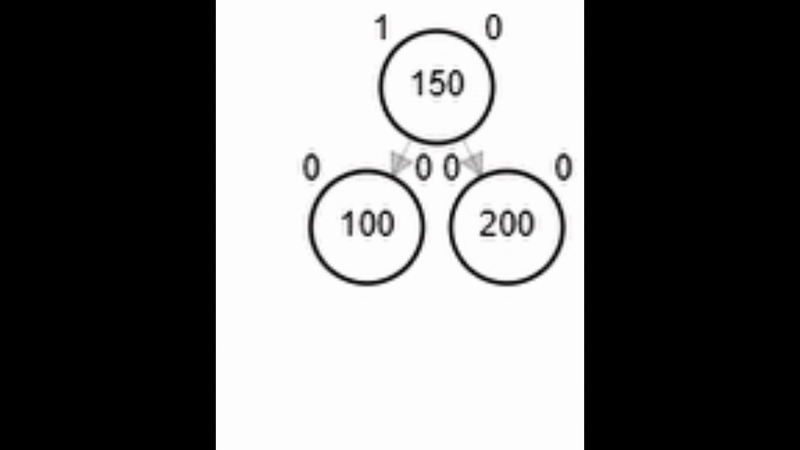
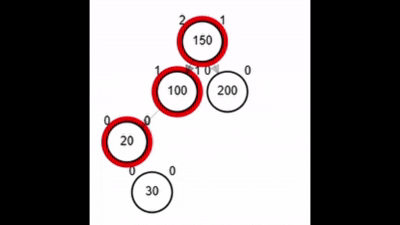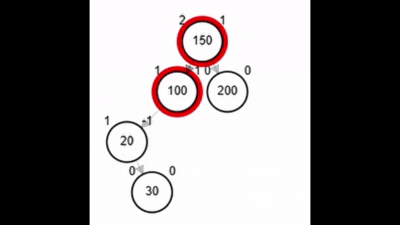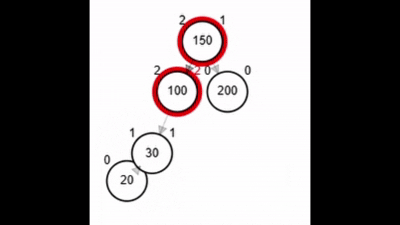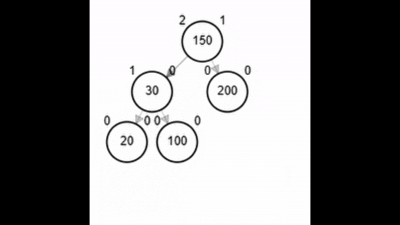
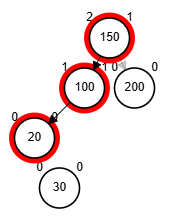
Rotaciones

Rotación doble: izquierda derecha.

¿?

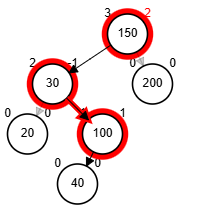
node.izq <-- rSI(node.izq)
retorna rSD(node)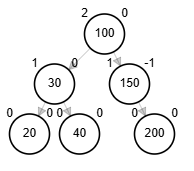

Rotaciones

Rotación doble: derecha - izquierda.

node.der <-- rSD(node.der)
retorna rSI(node)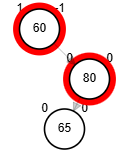

¿?

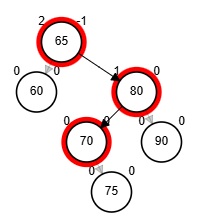
Inserción AVL

function addNodeAVLR(Node node, Ent: x)
|	//Casos bases --> Llamados NO recursivos
|	if(node = null) // Se ha recorrido todo el árbol y no se ha encontrado se debe añadir.
|	|	return newNode(x)
|	end-if
|   if(node.data == x)//Se ha encontrado el elemento
|	|	ESC("El elemento ", x, " ya existe")
|	|	return node
|	end-if	
|	//LLamados recursivos
|	if(node.data > x)// El dato a añadir es menor que el padre, avanzar hacia la izq
|	|	node.izq <-- addNodeAVLR(node.izq, x)
|	end-if
|	if(node.data < x)// El dato a añadir es mayor que el padre, avanzar hacia la der
|	|	node.der <-- addNodeAVLR(node.der, x)
|	end-if
|	node.balance <-- fb(node)
|	if(node.balance = -2)// rotación simple izquierda + rotación doble derecha - izquierda
|	|	if(node.der.balance = 1)
|	|	|	node.der <-- rSD(node.der)
|	|	end-if
|	|	return rSI(node)
|	end-if
|	if(node.balance = 2)// rotación simple derecha + rotación doble izquierda - derecha
|	|	if(node.izq.balance = -1)
|	|	|	node.izq <-- rSI(node.izq)
|	|	end-if
|	|	return rSD(node)
|	end-if
|	return node
end-function

Eliminación - AVL

Al eliminar un nodo, se puede dar el caso que el factor de equilibrio de un nodo de los sucesores del nodo desequilibrado sea cero. Por tanto, no se sabe qué rotación es posible aplicar.

Tener presente que: se elimina tal cual como un ABB, solo se le añade la validación sobre los factores de equilibrio.

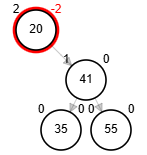
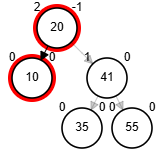
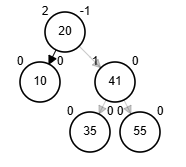
Delete 10

Eliminación - AVL

Posibles rotaciones:
- fb(node) = 2, aplicar alguna de las dos
  - Rotación simple izquierda sobre el nodo.
  - Aplicar rotación doble derecha - izquierda.
- fb(node) = -2, aplicar alguna de las dos
  - Rotación simple derecha sobre el nodo.
  - Aplicar rotación doble izquierda- derecha.

Eliminación - AVL

Por simplicidad, tomaremos para eliminación cuando sus sucesores tengan fb igual a 0.

Posibles rotaciones:
- fb(node) = 2
  - Rotación simple derecha sobre el nodo.
- fb(node) = -2, aplicar alguna de las dos
  - Rotación simple izquierda sobre el nodo.

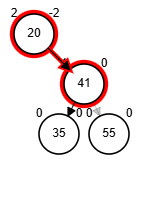
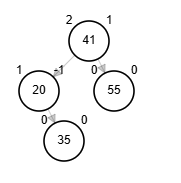
Eliminación - AVL

function deleteNodeAVLR(Node node, Ent: x)
|	//Casos bases --> Llamados NO recursivos
|	if(node = null) // Se ha recorrido todo el árbol y no se ha encontrado
|	|	ESC("No se ha encontrado el elemento ", x)
|	|	return null
|	end-if
|	//LLamados recursivos
|	if(node.data > x)// El dato a eliminar es menor que el padre, avanzar hacia la izq
|	|	node.izq <-- deleteNodeAVLR(node.izq, x)
|	end-if
|	if(node.data < x)// El dato a eliminar es mayor es mayor que el padre, avanzar hacia la der
|	|	node.der <-- deleteNodeAVLR(node.der, x)
|	end-if
|   if(node.data == x)//Se ha encontrado el elemento
|	|	if(node.left = null)
|	|	|	return node.right
|	|	end-if
|	|	
|	|	if(node.right = null)
|	|	|	return node.left
|	|	end-if
|	|	Node sucesor <-- minSubDer(node.der)
|	|	node.data <-- sucesor.data
|	|	node.der <-- deleteR(node.der, sucesor.data)
|	end-if
|	node.balance <-- fb(node)
|	if(node.balance = -2)// rotación simple izquierda + rotación doble derecha - izquierda
|	|	if(node.der.balance = 1)
|	|	|	node.der <-- rSD(node.der)
|	|	end-if
|	|	return rSI(node)
|	end-if
|	if(node.balance = 2)// rotación simple derecha + rotación doble izquierda - derecha
|	|	if(node.izq.balance = -1)
|	|	|	node.izq <-- rSI(node.izq)
|	|	end-if
|	|	return rSD(node)
|	end-if
|	return node
end-function

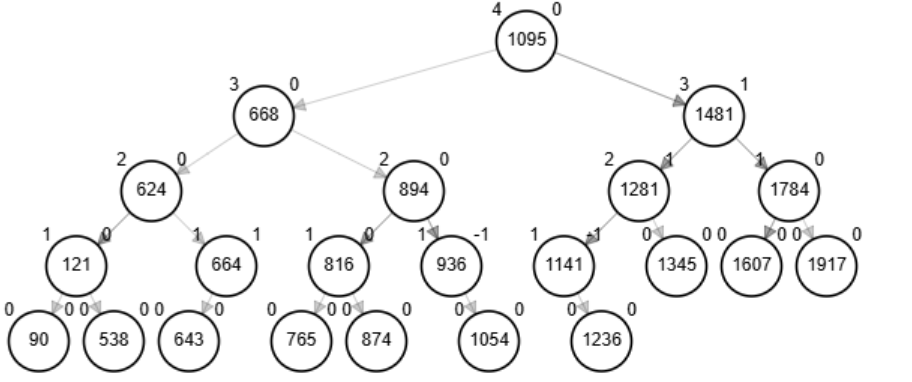
Ejemplo - Inserción

Grafique y especifique las rotaciones necesarias para crear un AVL con los siguientes nodos:

538, 624, 1607, 1481, 90, 1141, 668, 121, 456, 1095, 1917, 874, 1281, 664 643, 1345, 130, 927, 909, 253, 979, 1867, 1209, 816, 1784, 894, 1236, 936, 765, 1054

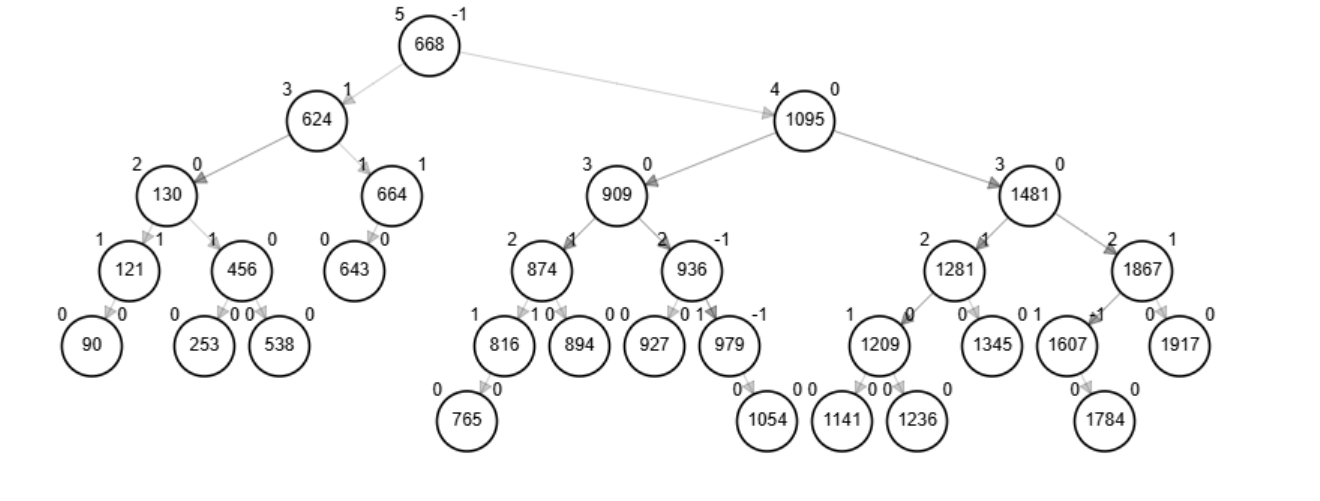
Ejemplo - Eliminación

Grafique y especifique las rotaciones necesarias para eliminar del AVL por predecesor

los siguientes nodos: 130 927 909 253 979 1867 1209 456.

Rotaciones - Resumen

Rotación	Condición
Simple izquierda	fb(node) = -2
Simple derecha	fb(node) = 2
Doble izquierda - derecha	fb(node) = 2 y fb(node.izq) = -1
Doble derecha- izquierda	fb(node) = -2 y fb(node.der) = 1

Árboles B

Creados en 1972 por R. Bayer y E. McCreight.
Generalizan el concepto de ABB a árboles de búsqueda n-arios.
Son ideales para operaciones de lectura y escritura en disco debido a su capacidad para minimizar el número de accesos a disco.
Pueden manejar grandes volúmenes de datos de manera eficiente.
Existen variantes como los árboles B+ y B* que optimizan ciertas operaciones o estructuras para casos específicos.

En un árbol B de orden P, cada nodo puede tener como máximo P hijos.
La raíz tiene al menos dos hijos si no es un nodo hoja.
Todos los nodos hoja están en el mismo nivel.
Un nodo no hoja con k hijos contiene k - 1 elementos almacenados.
Cada nodo (excepto la raíz) tiene como mínimo
d = ((P - 1) // 2) claves (valores).

Propiedades de Árboles B

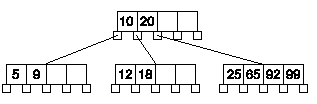
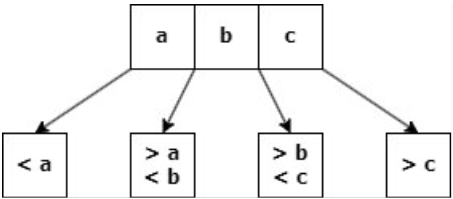
Ejemplo: P = 5 ; d = 2

Los hijos de cualquier nodo deben cumplir con:

El primer hijo tiene valores menores que a.
El segundo hijo tiene valores mayores que a y menores que b.
El último hijo tiene valores mayores que c.

Propiedades de Árboles B

Operaciones

Búsqueda: Similar a la búsqueda en ABB, solo se debe decidir por cuál rama seguir dependiendo el dato que se busque.
Inserción: Se debe considerar si quedan espacios disponibles en el nodo donde se debe insertar la clave.
Eliminación: Se debe considerar el valor mínimo de claves por nodo, por lo que es posible que se necesite reequilibrar el árbol.

Búsqueda

function buscarEnArbolB(Nodo nodo, Ent: clave)
|   //Caso base: Si el nodo es null, la clave no está en el árbol
|   if (nodo = null)
|   |   ESC("No se ha encontrado la clave ", clave)
|   |   return null
|   end-if
|
|   // Buscar la clave en el nodo actual
|   Para i desde 1 hasta nodo.numClaves
|   |   if (clave = nodo.claves[i])
|   |   |   ESC("Clave encontrada en el nodo")
|   |   |   return nodo
|   |   end-if
|   |   if (clave < nodo.claves[i])
|   |   |   // La clave puede estar en el subárbol izquierdo
|   |   |   return buscarEnArbolB(nodo.hijos[i], clave)
|   |   end-if
|   end-for
|
|   // La clave puede estar en el subárbol derecho del último hijo
|   return buscarEnArbolB(nodo.hijos[nodo.numClaves + 1], clave)
end-function

Inserción

Realizando una búsqueda en el árbol, se halla el nodo hoja en el cual debería ubicarse el nuevo elemento.
Si el nodo hoja tiene espacios libres, entonces inserte el nuevo elemento en el nodo, respetando el orden de los elementos.
Si el nodo NO tiene espacios libres:

Se escoge el valor medio entre los elementos de la hoja y el elemento a insertar
El valor medio asciende al nodo padre en el orden correspondiente. Si no hay nodo padre se crea.
La nueva clave se inserta en la partición correspondiente (en el orden adecuado).

Si en el padre no se pueden insertar más claves, entonces se debe repetir recursivamente la partición de los nodos hasta poder insertar la nueva clave.

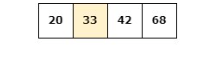
Add 27

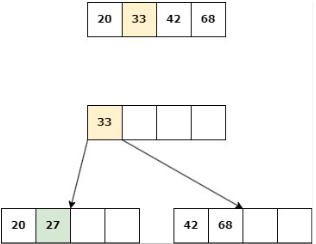
Inserción

Insertar en un árbol de orden P = 4 las siguientes claves:

37, 14, 60, 9, 22, 51, 10, 5, 55, 70, 1, 25

Ejercicio

Ejercicio Resuelto

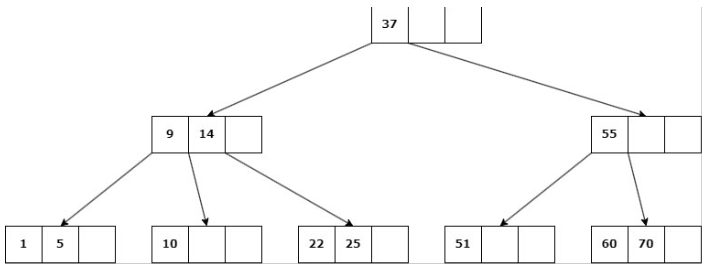
Eliminación

Buscar la clave a eliminar. Si la clave existe se trabajará con el nodo correspondiente.
Dependiendo de la cantidad mínima de claves (d) en dicho nodo, se pueden dar los siguientes casos:

Si el nodo es una hoja:

Si tiene más de d claves.
Si tiene d claves.

Si el nodo no es una hoja:

Si uno de los hijos inmediatos de la clave a eliminar tiene más de d claves
Si ninguno de los hijos inmediatos de la clave a eliminar tiene más de d claves.

Si la eliminación causa que la altura del árbol disminuya.

Caso 1: Nodo hoja con más de d claves.

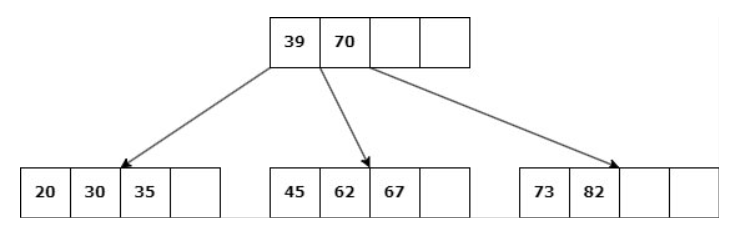
Delete 67

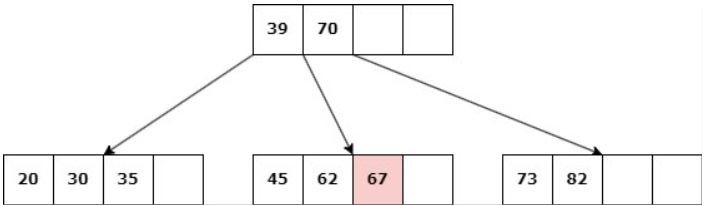
Simplemente se elimina la clave

Caso 1: Nodo hoja con d claves.

Delete 45

a. Si un nodo hermano tiene más de d claves, entonces se produce un “préstamo” de claves: Se elimina la clave, una clave del padre desciende al hijo y una clave del hermano asciende al padre.

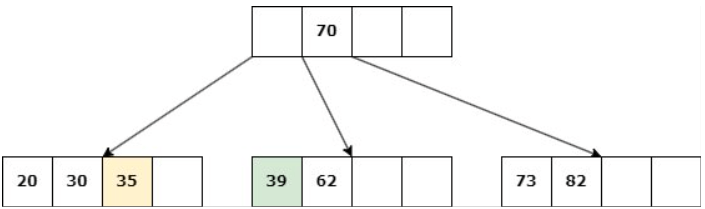
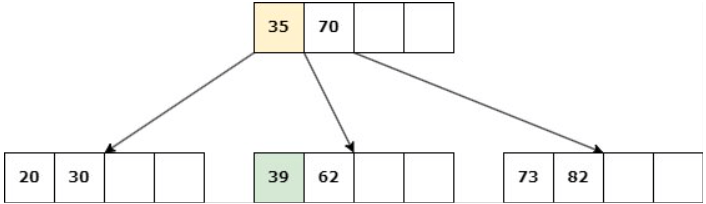
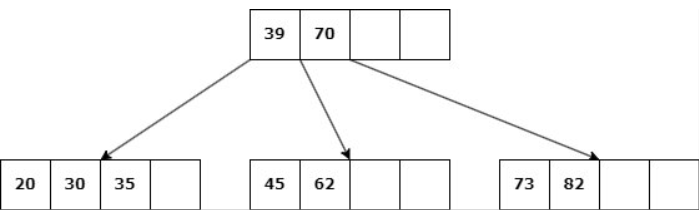
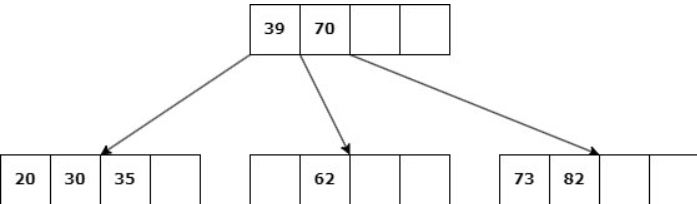
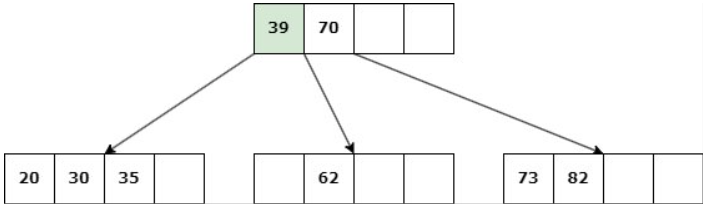
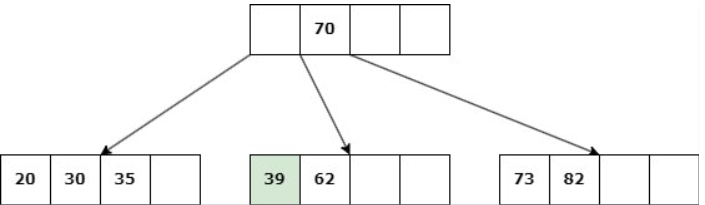
Caso 1: Nodo hoja con d claves.

Delete 39

b. Si ningún nodo hermano tiene más de d claves, entonces se une la hoja con uno de estos: Se elimina la clave, las claves del hermano se copian al nodo y la clave del padre entre ambos desciende al hijo.

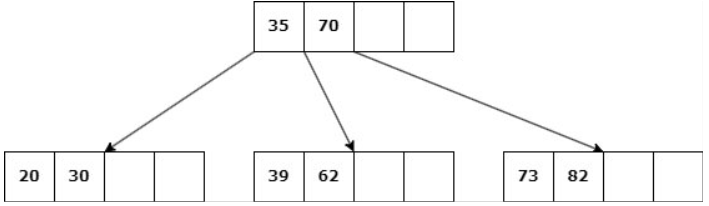
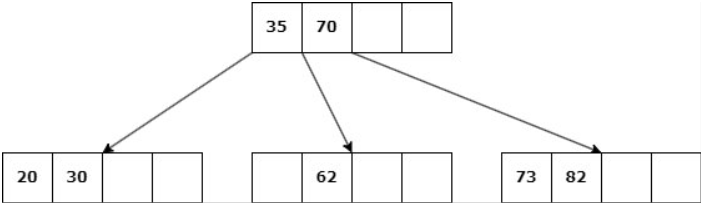
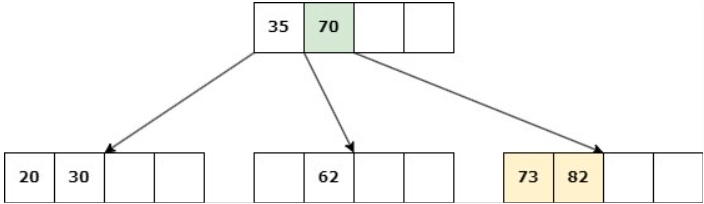
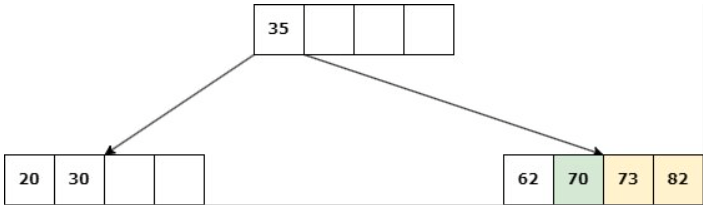
Caso 2: Nodo NO hoja

Delete 14

a. Si uno de los hijos inmediatos de la clave a eliminar tiene más de d claves, entonces se debe reequilibrar el árbol: Se suprime la clave y una clave del hijo asciende al padre.

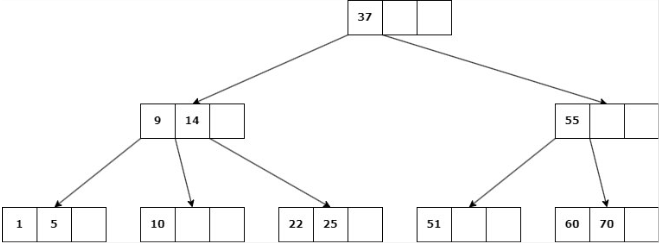
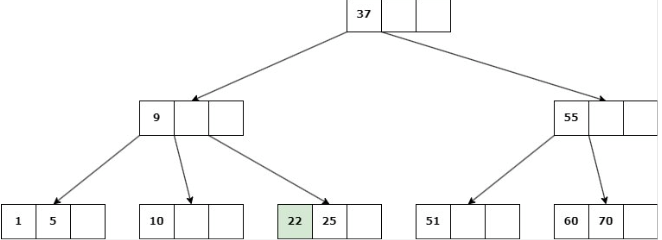
Caso 2: Nodo NO hoja

Delete 22

b. Si ninguno de los hijos inmediatos de la clave a eliminar tiene más de d claves, entonces se deben unir los hijos: Se elimina la clave y se unen los 2 hijos en un solo nodo.

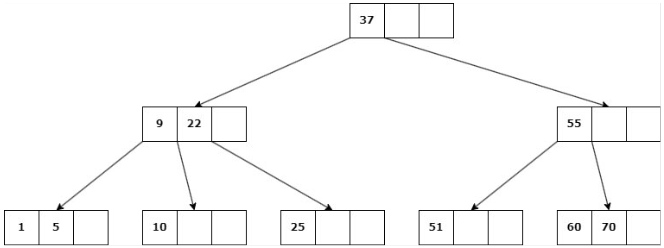
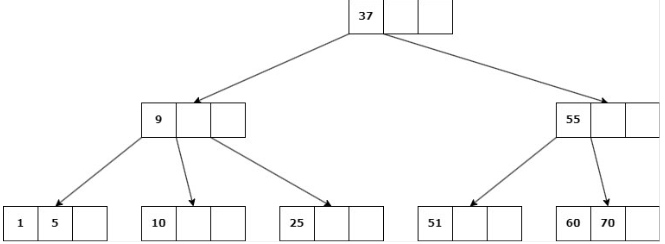
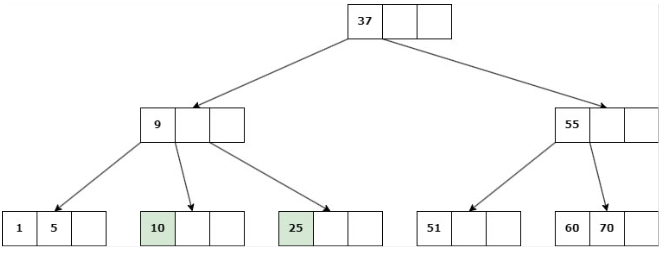
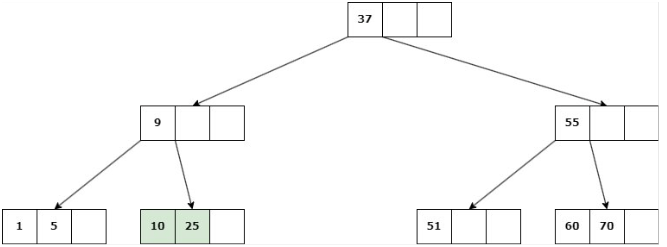
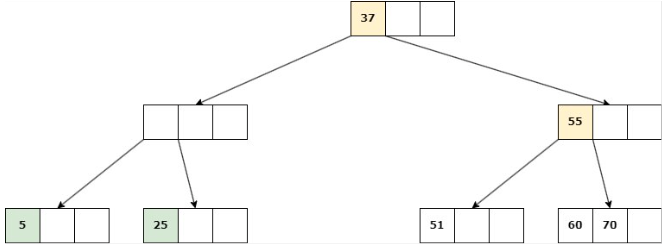
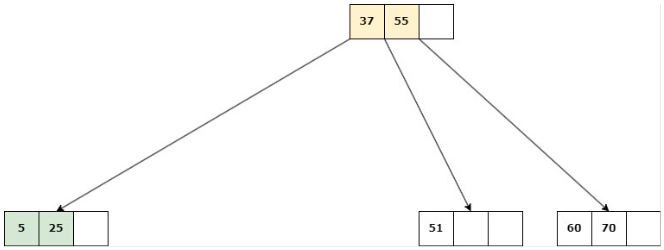
Caso 3: La eliminación cause que la altura del árbol disminuya

Se suprime la clave, se unen los hijos del nodo en uno solo y su padre se une a la información de su hermano.

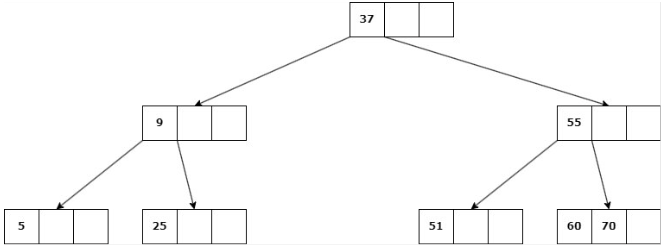
Delete 9

Ejercicios

Dibuja el árbol B de orden 5 que resulta de realizar las siguientes inserciones: 1, 7, 6, 2, 11, 4, 8, 13, 10, 5, 19, 9, 18, 24, 3, 12, 14, 20 y 21
A continuación elimina los elementos: 8, 10 y 6

Grafos

Generalidades
Fundamentos
Representación
Recorridos

Más sobre grafos

¿Que és un grafo?

Un grafo es una estructura de datos compuesta por un conjunto de vértices (también llamados nodos) y un conjunto de aristas (o arcos), que representan relaciones entre los vértices.

Notación

V de vértices o nodos del grafo, los cuales representan objetos.

V = \{v_0, v_1, v_2, \dots , v_{n-1} \}

y el conjunto E de aristas que representan relaciones entre objetos.

Si los pares de vértices que forman una arista son ordenados, entonces la arista es dirigida y se representa por

Si los pares de vértices que forman una arista no son ordenados, entonces no es dirigida y se representa por

E = \{(v_i,v_j), \dots ,(v_i,v_j) \}

(v_i,v_j)

\{v_i,v_j\}

E = \{ \{v_i,v_j\}, \dots ,\{v_i,v_j\} \}

Una arista puede tener asociado un factor de peso.

G = (V,E)

Definimos a

como el grafo G conformado por el conjunto

V(G)

E(G)

Asismismo,

Son todos los vértices en G

Son todos las aristas en G las cuales representan las adyacencias del mismo

Ejemplo de grafo

V = \{ 1, 4, 5, 7, 9\}

E = \{ \{ 1,4\}, \{ 4,9\} , \{ 9,7\}, \{ 7,5\}, \{ 5,1\} \}

V = \{ 0, 1, 2, 3, 4\}

E = \{ (0,3), (1,2), (1,0), (3,2), (3,1), (4,0) \}

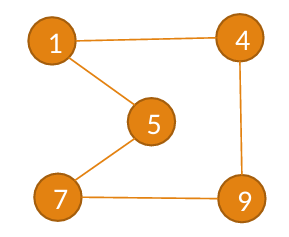
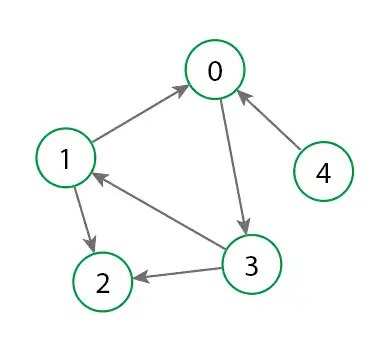
Aplicaciones

Los grafos permiten estudiar interrelaciones entre elementos que interactúan unos con otros

Son aplicables en:

Ingeniería de Sistemas
Modelado de Redes.
Ingeniería Industrial, Electrónica.
Química
Geografía
Redes neuronales
Etc.

Tipos de grafos

Simple

Dirigido

No Dirigido

Multigrafo

Ponderado

Completo

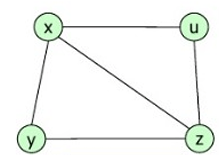
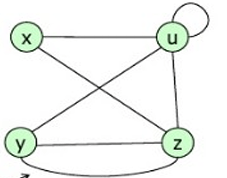
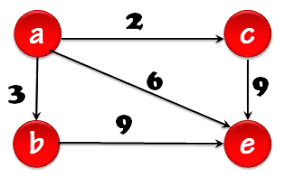
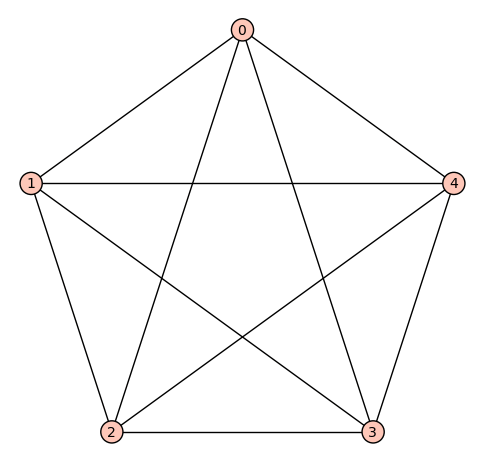
Fundamentos

En un grafo no dirigido:

El grado de un vértice v, es el número de aristas que contienen a v, notado como

En un grafo dirigido:

El grado de entrada de un vértice v, es el número de aristas que llegan a v, notado como
El grado de salida de un vértice v, es el número de aristas que salen de v, notado como

grad(v)

grad_i(v)

grad_o(v)

Ejemplo

grad(4) = 2

grad(6) =

grad(7) =

grad(9) =

grad(10) =

grad(11) =

grad_i(0)=2

grad_i(1)=

grad_i(2)=

grad_i(3)=

grad_i(4)=

grad_o(0)=1

grad_o(1)=

grad_o(2)=

grad_o(3)=

grad_o(4)=

\sum_{v \in V} grad(v) = ?

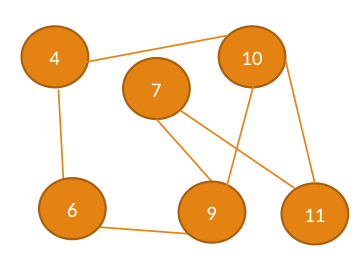
Fundamentos

Camino

Secuencia finita de vértices donde cada par consecutivo está conectado por una arista (puede repetir vértices/aristas).

Longitud del camino:

El número de arcos que lo forman.

Camino simple:

Camino que NO REPITE vértices. Los extremos pueden ser iguales.

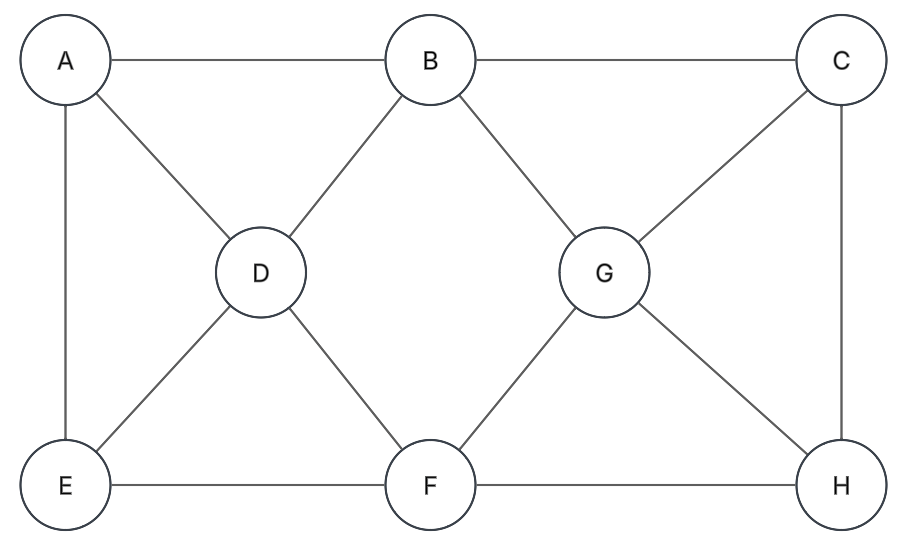
Fundamentos

Ciclo / Circuito (camino cerrado): Es un camino que inicia y termina en el mismo nodo. Al menos tiene 3 vértices.

Ciclo simple:

Es un ciclo donde todos sus vértices y aristas son distintos.

Bucle:

Arista que va desde un vértice en

a sí mismo.

V(G)

Fundamentos

P_1 = (V,X,Z)

P_2 = (U, W, X, Y, W, V)

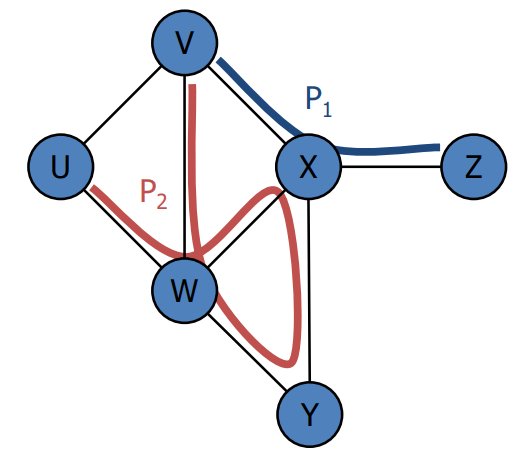
Es un camino simple de longitud 3

No es un camino simple de longitud 6

P_3 = (U, W, X, V, U)

Es un camino cerrado de longitud 5

Fundamentos

Grafo k-regular:

Grafo donde todos los vértices tienen grado k.

Bipartito: Es un grafo que se puede expresar en dos conjuntos donde cada arista los conecta pero no hay aristas entre vértices del mismo conjunto.

Grafo completo: Kn

Grafo (n-1) regular con n vértices, y cada vértice está conectado a todos los demás:

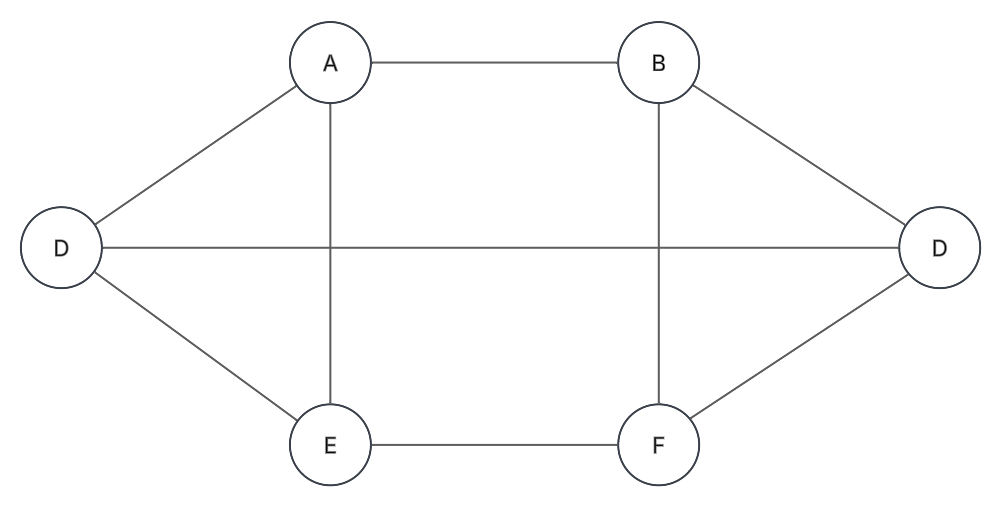
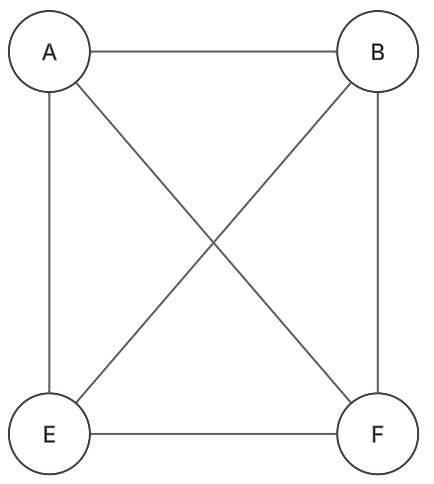
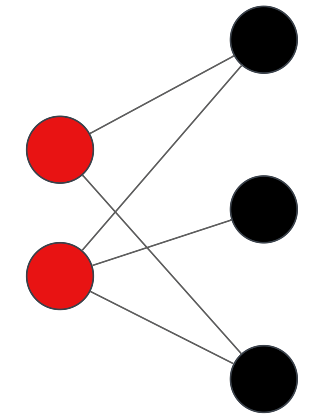
Fundamentos

Grafo conexo:
- Grafo NO dirigido:
  - Si existe un camino entre cualquier par de vértices que forman el grafo.

Grafo conexo:
- Grafo dirigido:
  - Fuertemente conexo: existe un camino entre cualquier par de vértices.
  - Débilmente conexo: existe una cadena entre cualquier par de vértices

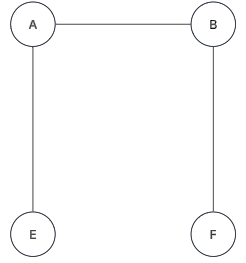
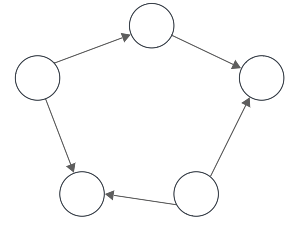
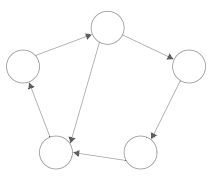
Representación

Objetos:
- Tiene un campo con la info del vértice.
- Tiene una lista donde se guardan los apuntadores de los vértices que son adyacentes.
Matriz de adyacencia:
- Matriz que contiene la información sobre las relaciones de adyacencia entre los vértices.
Lista de Adyacencia:
- Multilista simple que contiene la información sobre las relaciones de adyacencia entre cada par de vértices.

A \in \mathbb{R}^{|V| \times |V|}

Representación

Matriz de adyacencia:

A \in \mathbb{R}^{n \times n}

Sea

n = |V|

G(V,E)

un grafo donde

, suponemos entonces que los

vértices

V =\{v_0, v_1, \cdots, v_{n-1}\}

están ordenamos ascendentemente, y

podemos representarlos con sus ordinales:

\{0, 1, \cdots, n-1\}.

De lo anterior, podemos estructurar a la matriz de adyacencia A como sigue:

Grafos NO dirigidos:

con las entradas según el caso:

A[i][j] = 1 \text{ si } \{v_i, v_j\} \in E(G)

A = A^\intercal

A[i][j] = 0 \text{ si } \{v_i, v_j\} \not\in E(G)

Grafos dirigidos:

A[i][j] = 1 \text{ si } ({v_i, v_j}) \in E(G)

A[i][j] = 0 \text{ si } ({v_i, v_j}) \not\in E(G)

Otros tipos de matrices

Matriz de costos
- Matriz que aloja los pesos de cada una de las aristas de un grafo.

Matriz de Distancias:
- Matriz que aloja la distancia de los (caminos mínimos) de un vértice a otro.

Matriz de Aristas:
- Matriz que aloja los vértices iniciales y finales para cada una de las aristas.

Matriz de Incidencia:
- Matriz que aloja la incidencia de las aristas en los vértices.

% M \in |V| \times |E|

C \in \mathbb{R} ^ {|V| \times |V|}

D \in \mathbb{R} ^ {|V| \times |V|}

B \in \mathbb{R} ^ {|E| \times 2}

M \in \mathbb{R} ^ {|V| \times |E|}

Otros tipos de matrices

Matriz de costos
- Matriz que aloja los pesos de cada una de las aristas de un grafo.

Matriz de Distancias:
- Matriz que aloja la distancia de los (caminos mínimos) de un vértice a otro.

Matriz de Aristas:
- Matriz que aloja los vértices iniciales y finales para cada una de las aristas.

Matriz de Incidencia:
- Matriz que aloja la incidencia de las aristas en los vértices.

% M \in |V| \times |E|

C \in \mathbb{R} ^ {|V| \times |V|}

D \in \mathbb{R} ^ {|V| \times |V|}

B \in \mathbb{R} ^ {|E| \times 2}

M \in \mathbb{R} ^ {|V| \times |E|}

Matriz de adyacencia

% M \in |V| \times |E|

0	1	0
1	0	1
0	0	0

0	1	0	2	0
1	0	1	3	4
4	6	0	30	15
25	1	8	0	99
87	65	95	18	0

0	1	1	1	1
1	0	0	0	1
1	0	0	1	1
1	0	1	0	0
1	1	1	0	0

Matriz de adyacencia

% M \in |V| \times |E|

Es importante destacar que la matriz de adyacencia es poco eficiente cuando:
1. número de vértices no es fijo.
2. Hay pocas conexiones entre los nodos del grafo. (Sparse Matrix)

Lista de adyacencia

Multilista simple que contiene la información sobre las relaciones de adyacencia entre cada par de vértices.
- La lista simple principal tiene la información del vértice, un apuntador a una lista secundaria de aristas y un apuntador hacia el siguiente vértice del grafo.
- Son más eficientes con el espacio si el grafo tiene pocas aristas.

% M \in |V| \times |E|

Lista de adyacencia

% M \in |V| \times |E|

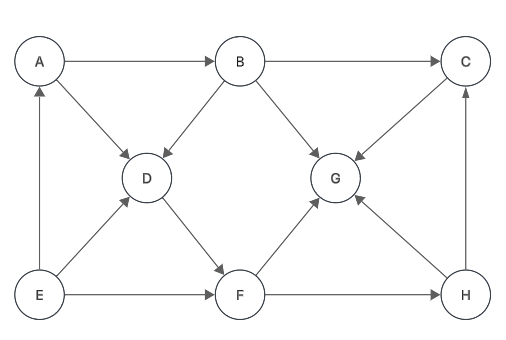
Recorridos

DFS - Depth First Search
- Equivalente al Preorden
- Se debe partir de un nodo dado
Algoritmo:

SUB DFS(nodo_actual)
|   visited.add(nodo_actual)
|   ESC("Visitando: " + nodo_actual.valor)
|   for each vecino in grafo.adyacentes(nodo_actual)
|   |   if vecino not in visited
|   |   |   DFS(vecino)
|   |   end-if
|   end-for
END-SUB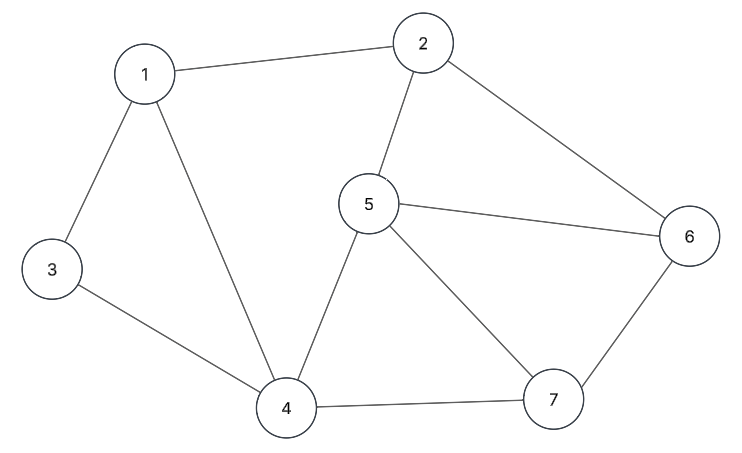

% M \in |V| \times |E|

BFS - Breadth First Search
- Equivalente a recorrer por niveles
- Se debe partir de un nodo dado.
Algoritmo:

SUB BFS(nodo_inicial)
|   queue = new Queue()
|   visited = new Set()
|   
|   queue.enqueue(nodo_inicial)
|   visited.add(nodo_inicial)
|
|   while queue no esté vacía
|   |   nodo_actual = queue.dequeue()
|   |   ESC("Visitando: " + nodo_actual.valor)
|
|   |   for each vecino in grafo.adyacentes(nodo_actual)
|   |   |   if vecino not in visited
|   |   |   |   visited.add(vecino)
|   |   |   |   queue.enqueue(vecino)
|   |   |   end-if
|   |   end-for
|   end-while
END-SUB

Grafos

Camino mínimo
Árboles de expansión
Flujo máximo

Camino mínimo

G = (V,E)

Dado el grafo

con:

V: conjunto de vértices
E: conjunto de aristas con
s: nodo origen o inicio

Se desea encontrar el camino

w(e), \forall e \in E

P = (s, v_1, v_2, \cdots , t)

que minimice la suma

los pesos, es decir:

P^* := min \sum_{i=1}^{k} w(v_{i-1}, v_i)

Donde:

v_0 = s, v_k = d

Tener presente que:

Pueden existir varios caminos para llegar de un vértice a otro.
- Los caminos pueden ser iguales.
Se pueden encontrar caminos mejores a lo ya existentes

Algoritmos a evaluar

Dijkstra
Floyd-Warshall

Dijkstra

Válido para grafos dirigidos y NO dirigidos con pesos positivos.
Se encontrarán los caminos mínimos y sus distancias desde un vértice inicial a todos los posibles destinos.
Utilizaremos una cola de prioridad basada en min-heap
- Permite extraer el nodo con la menor distancia en tiempo
*Aplicado por Google para encontrar la ruta mínima entre 2 puntos *

v_0

\log(n)

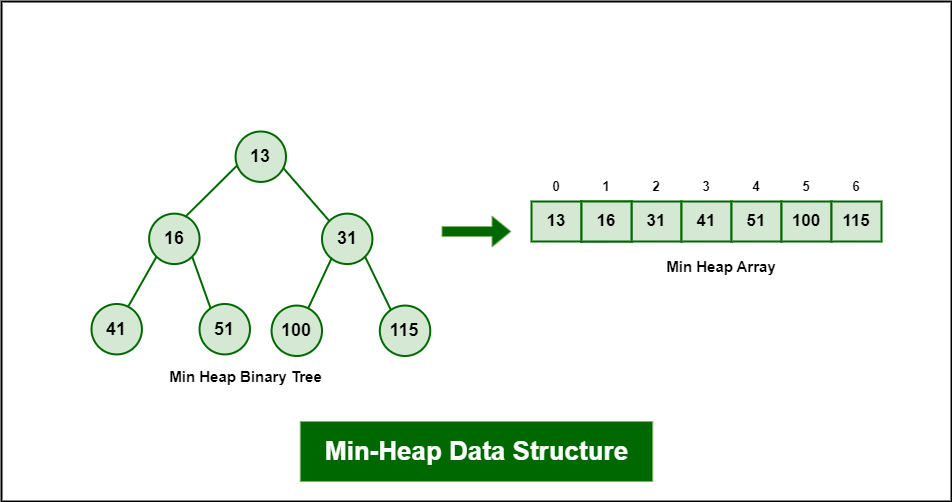
* Adapto bajo heurísticas

Dijkstra

SUB DIJKSTRA(grafo G, nodo_fuente s)
|   distancia = new Dictionary()
|   padre = new Dictionary()
|   visto = new Set()
|   cola_prioridad = new PriorityQueue()
|   for each nodo u in G.nodos
|   |   distancia[u] = INFINITO
|   |   padre[u] = NULL
|   end-for
|   distancia[s] = 0
|   cola_prioridad.enqueue((s, 0))
|   while cola_prioridad no esté vacía
|   |   (u, dist_actual) = cola_prioridad.dequeue()
|   |   if u not in visto
|   |   |   visto.add(u)
|   |   |   for each vecino v in G.adyacentes(u)
|   |   |   |   peso_uv = G.peso(u, v)
|   |   |   |   nueva_dist = distancia[u] + peso_uv
|   |   |   |   if nueva_dist < distancia[v]
|   |   |   |   |   distancia[v] = nueva_dist
|   |   |   |   |   padre[v] = u
|   |   |   |   |   cola_prioridad.enqueue((v, nueva_dist))
|   |   |   |   end-if
|   |   |   end-for
|   |   end-if
|   end-while
END-SUB

\infty

	A	B	C	D	E	F	G
distan
padre
visto

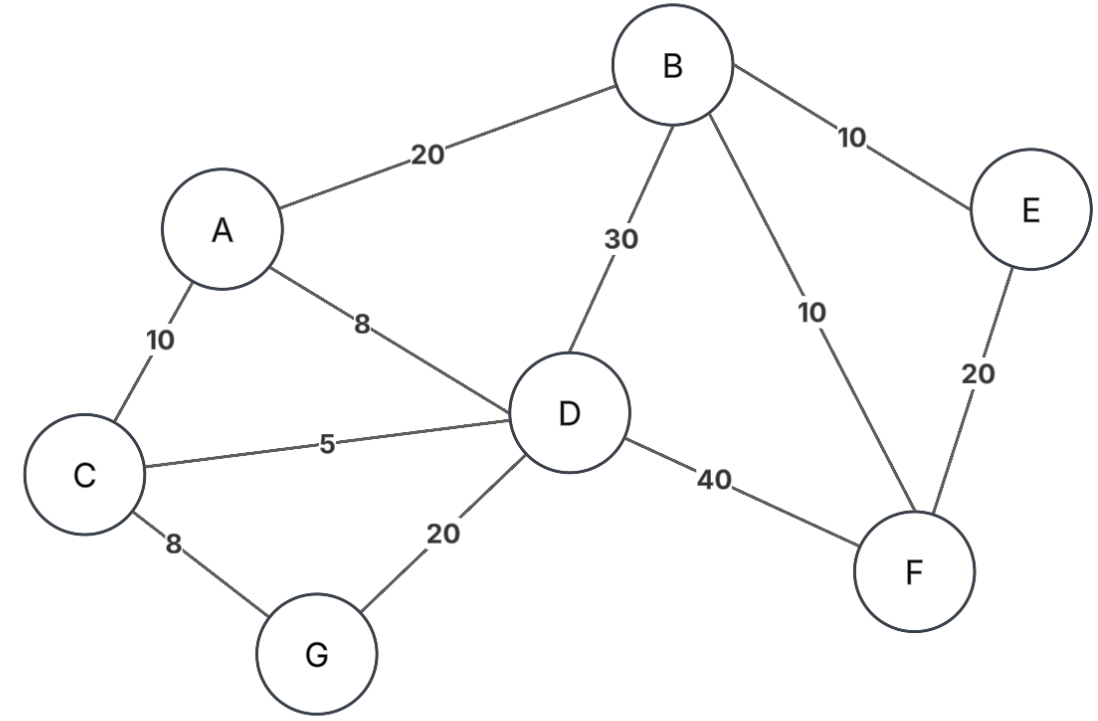
Floyd-Warshall

Válido para grafos dirigidos y NO dirigidos.
Se encontrarán ahora todos los caminos mínimos y sus distancias desde cada par de vértices en el grafo
Se necesita de una matriz de distancias D
- Cada valor se reemplaza por el valor mínimo de la suma de los elementos que representan la inserción de valores analizados
Adicional, una matriz de caminos P.
- Inicialmente, cada columna contiene al elemento de su columna.
- Cada valor se reemplaza por el pivote que represente el valor mínimo de la suma de los elementos que representan la intersección de valores analizados.

Floyd-Warshall

// Inicialización:
Para cada nodo vi en V(G):           // Para cada vértice de origen
    Para cada nodo vj en V(G):       // Para cada vértice de destino
        Si vi == vj:
            D[vi][vj] = 0            // Distancia a sí mismo es 0
            P[vi][vj] = vi           // Camino a sí mismo es él mismo
        Si existe arista vi -> vj:
            D[vi][vj] = peso(vi -> vj) // Distancia directa
            P[vi][vj] = vj           // Siguiente nodo es vj
        Sino:
            D[vi][vj] = ∞            // Infinito si no hay conexión
            P[vi][vj] = -          // No hay camino

// Floyd-Warshall: Explorar todos los caminos posibles
Para cada nodo vk en V(G):           // Nodo intermedio
    Para cada nodo vi en V(G):        // Origen
        Para cada nodo vj en V(G):    // Destino
            // Verificar que exista camino por vk y sea mejor
            Si D[vi][vk] + D[vk][vj] < D[vi][vj]:
                D[vi][vj] = D[vi][vk] + D[vk][vj]  // Actualizar distancia
                P[vi][vj] = P[vi][vk]              // Actualizar camino

Floyd-Warshall

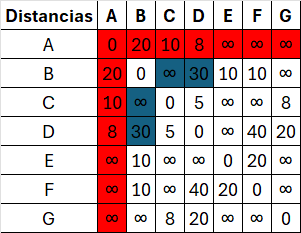
	A	B	C	D	E	F	G
A	0	20	10	8	∞	∞	∞
B	20	0	∞	30	10	10	∞
C	10	∞	0	5	∞	∞	8
D	8	30	5	0	∞	40	20
E	∞	10	∞	∞	0	20	∞
F	∞	10	∞	40	20	0	∞
G	∞	∞	8	20	∞	∞	0

Matriz D

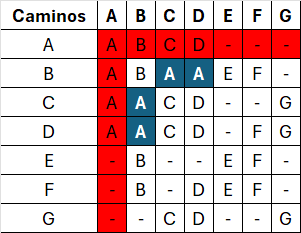
Matriz P

	A	B	C	D	E	F	G
A	A	B	C	D	-	-	-
B	A	B	-	D	E	F	-
C	A	-	C	D	-	-	G
D	A	B	C	D	-	F	G
E	-	B	-	-	E	F	-
F	-	B	-	D	E	F	-
G	-	-	C	D	-	-	G

Si D[vi][vk] + D[vk][vj] < D[vi][vj]:
  D[vi][vj] = D[vi][vk] + D[vk][vj]  // Actualizar distancia
  P[vi][vj] = P[vi][vk]              // Actualizar camino

	A	B	C	D	E	F	G
A	0	20	10	8	30	30	18
B	20	0	30	28	10	10	38
C	10	30	0	5	40	40	8
D	8	28	5	0	38	38	13
E	30	10	40	38	0	20	48
F	30	10	40	38	20	0	48
G	18	38	8	13	48	48	0

	A	B	C	D	E	F	G
A	A	B	C	D	B	B	C
B	A	B	A	A	E	F	A
C	A	A	C	D	B	B	G
D	A	A	C	D	B	B	C
E	B	B	B	B	E	F	B
F	B	B	B	B	E	F	B
G	C	C	C	C	C	C	G

v_k = A

Si D[vi][vk] + D[vk][vj] < D[vi][vj]:
  D[vi][vj] = D[vi][vk] + D[vk][vj]// Actualizar distancia
  P[vi][vj] = P[vi][vk]			   //Actualizar camino

v_k = B

Si D[vi][vk] + D[vk][vj] < D[vi][vj]:
  D[vi][vj] = D[vi][vk] + D[vk][vj]// Actualizar distancia
  P[vi][vj] = P[vi][vk]			   //Actualizar camino

v_k = C

Si D[vi][vk] + D[vk][vj] < D[vi][vj]:
  D[vi][vj] = D[vi][vk] + D[vk][vj]// Actualizar distancia
  P[vi][vj] = P[vi][vk]			   //Actualizar camino

v_k = D

v_k = E

v_k = F

v_k = G

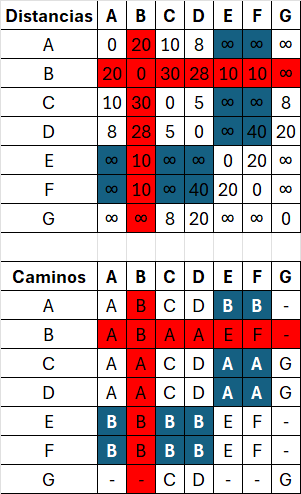
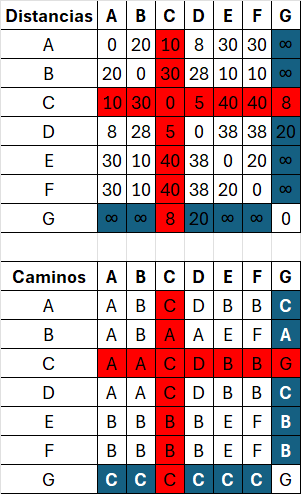
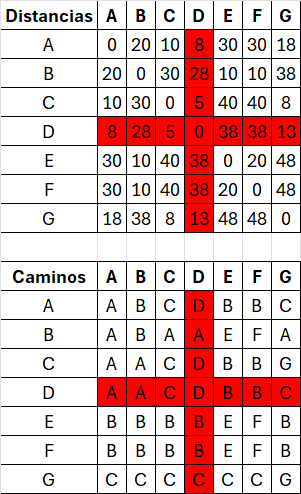
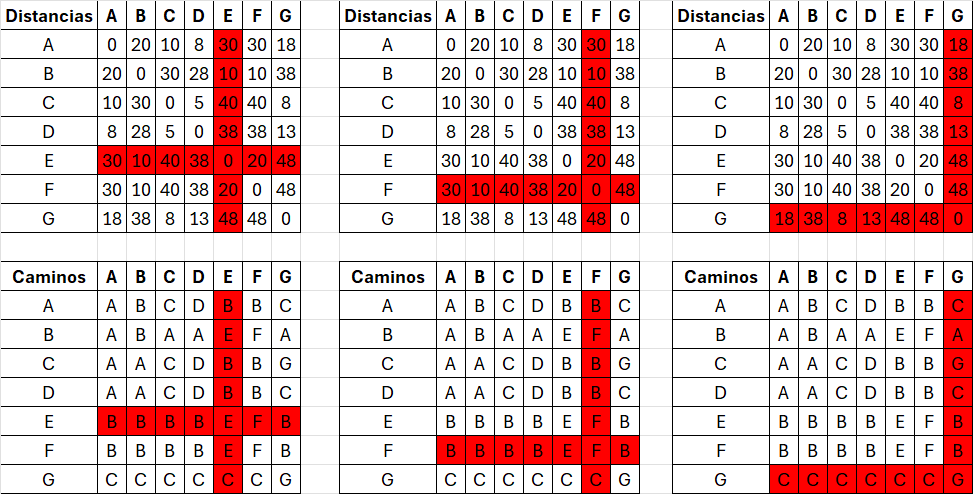
Si D[vi][vk] + D[vk][vj] < D[vi][vj]:
  D[vi][vj] = D[vi][vk] + D[vk][vj]// Actualizar distancia
  P[vi][vj] = P[vi][vk]			   //Actualizar camino

Métodos de ordenamiento

Los métodos de ordenamientos son algoritmos que permiten organizar los elementos de una lista o arreglo en un orden específico (ascendente o descendente).

Principales métodos de ordemiento:

Básicos
- Burbuja
- Selección
- Inserción

Avanzados
- Quick
- Merge
- Heap
- Bucket
- Radix

Especializados
- Counting
- Shell
- Tim

Burbuja - Bubble

Uno de los más fáciles de interpretar, pero con peor costo computacional.
Objetivo: Comparar pares de elementos adyacentes e intercambiarlos si están en el orden incorrecto.
Complejidad:

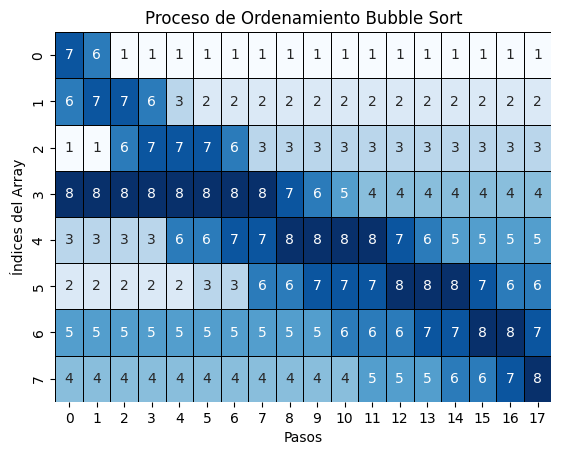
for i: 0 to length(data) - 2
	for j: i + 1 to length(data) - 1:
    	if data[i] > data[j]:
        	swap data[i] and data[j]

Selección

Objetivo: En cada iteración encontrar el elemento más pequeño del arreglo e ir intercambiándolo.
Complejidad:

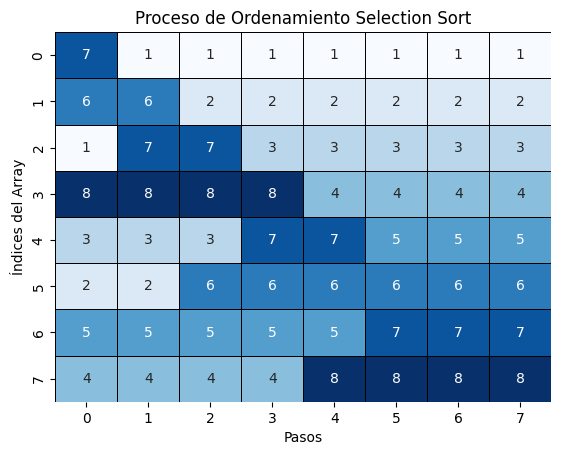
for i: 0 to length(data) - 2
	min_i = i
	for j: i + 1 to length(data) - 1:
    	if data[min_i] > data[j]:
        	min_i = j
    swap data[i] and data[min_i]

Inserción

Objetivo:
- Construir el arreglo ordenado en 1 solo.
- Se inserta cada elemento en su posición correcta dentro de la parte ya ordenada.
Complejidad:

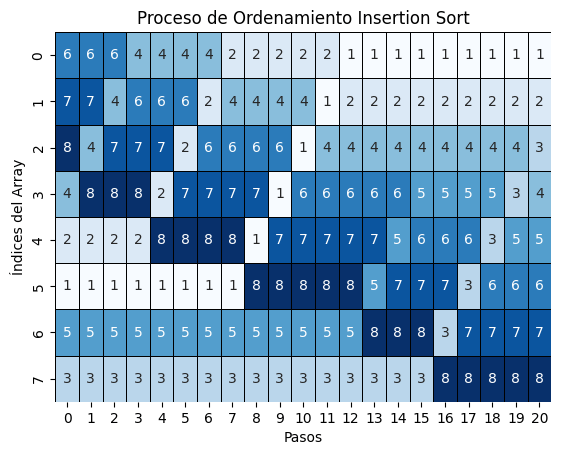
for i: 1 to length(data) - 1
	key = data[i]
	j = i + 1
    while j >= 0 and key < data[j]
    	data[j + 1] = data[j]
        j = j - 1
    data[j + 1] = key

Quick

Objetivo:
- Dividir el arreglo en 2 partes dadas por un elemento llamado pivote.
Algoritmo recursivo que sigue el paradigma divide and conquer.
Conocido por bajo tiempo de ejecución promedio
El peor caso puede llegar a
In-Place: No requiere estructura auxiliar
Complejidad:

procedure quicksort(data, low, high):
    if low < high:
        i = low
        j = high
        p = data[(low + high) // 2]  
        while i <= j:
            while data[i] < p:
                i += 1
            while data[j] > p:
                j -= 1
            if i <= j:
                swap(data[i], data[j])
                i += 1
                j -= 1
        
        # Recursión
        quicksort(data, low, j)
        quicksort(data, i, high)

\mathcal{O}(n^2)

Hilos y Sockets

Paralelismo
Hilos
Sockets

Paralelismo

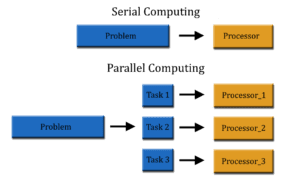
capacidad de un sistema para realizar varias operaciones al mismo tiempo, utilizando múltiples procesadores, núcleos o hilos. Su objetivo principal es mejorar el rendimiento y reducir el tiempo de ejecución.
Tipos:
- Paralelismo a nivel de instrucción: ejecutar varias instrucciones al mismo tiempo.
- Paralelismo a nivel de datos: realizar la misma operación sobre múltiples datos a la vez.
- Paralelismo a nivel de tareas: ejecutar diferentes tareas o funciones simultáneamente.

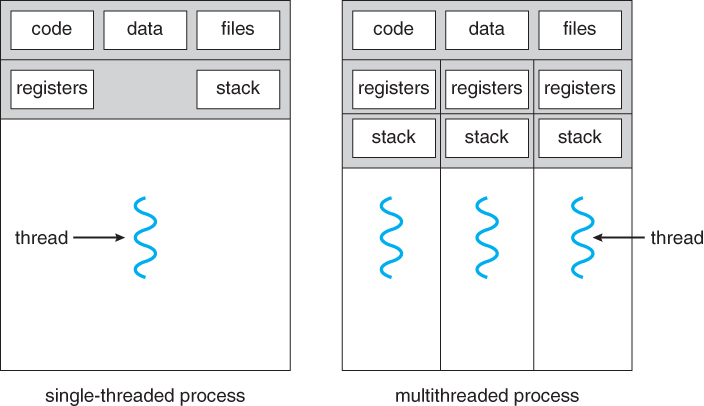
Hilos

Mecanismo para ejecutar bloques de código en paralelo.
- Las operaciones largas en un proceso no afectan a otro.
Un hilo es una pequeña secuencia de tareas ejecutada por el mismo.
El procesador solo puede realizar 1 tarea a la vez
- No hay paralelismo entre procesos a menos que haya tantos procesadores como tareas.
- Los hilos permiten la multitarea, ejecutando varios procesos simultáneamente.
Los hilos combinan líneas de dos o más procesos en uno solo.

Sockets

Mecanismo que permite la conexión entre distintos procesos.
Pueden ser utilizados para establecer comunicaciones entre distintas máquinas que estén conectadas a través de la red.

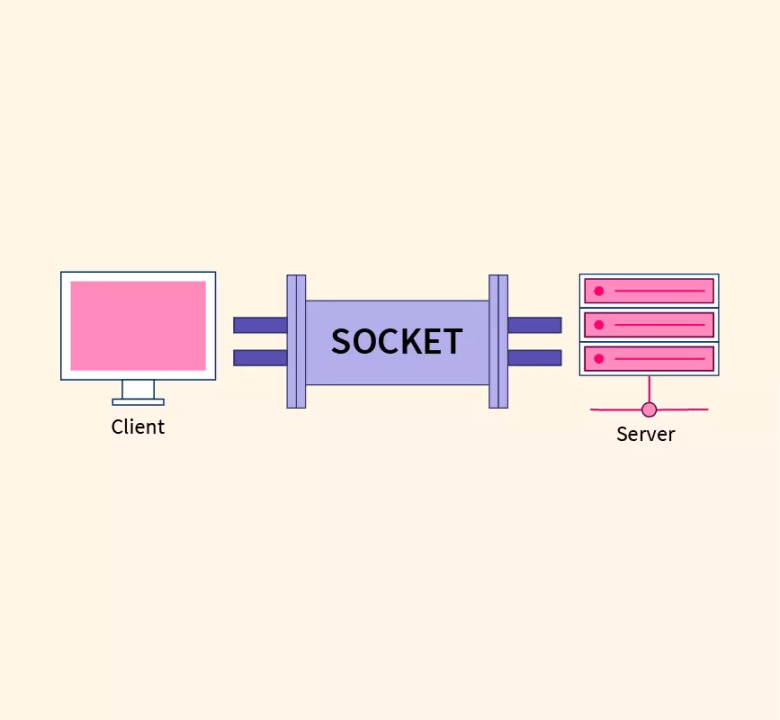
Cuando se utilizan sockets para comunicar procesos se basan en la arquitectura cliente-servidor.
- Se crean 2 sockets
  - Servidor: recibe la transmisión del cliente
  - Cliente: recibe respuesta del servidor

Sockets

Mecanismo que permite la conexión entre distintos procesos.
Pueden ser utilizados para establecer comunicaciones entre distintas máquinas que estén conectadas a través de la red.

Cuando se utilizan sockets para comunicar procesos se basan en la arquitectura cliente-servidor.
- Se crean 2 sockets
  - Servidor: recibe la transmisión del cliente
  - Cliente: recibe respuesta del servidor

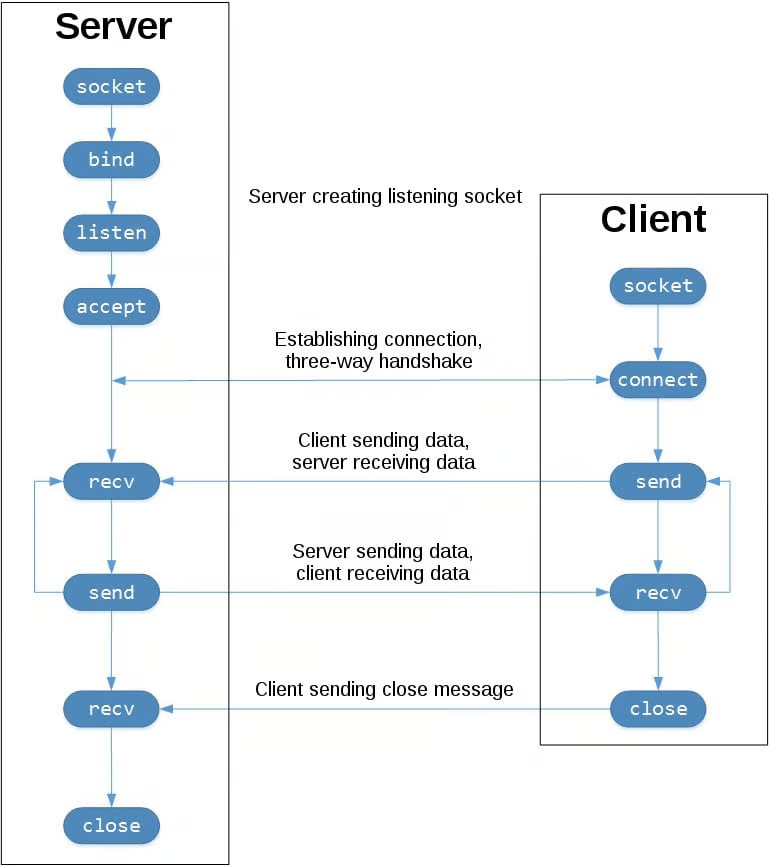
Sockets

Rol	Función	Descripción
Ambos	socket()	Crear el socket
Servidor	bind()	Asignar IP y puerto
Servidor	listen()	Esperar conexiones
Servidor	accept()	Aceptar conexión entrante
Cliente	connect()	Conectarse al servidor
Ambos	send() / recv()	Enviar y recibir datos
Ambos	close()	Cerrar la conexión

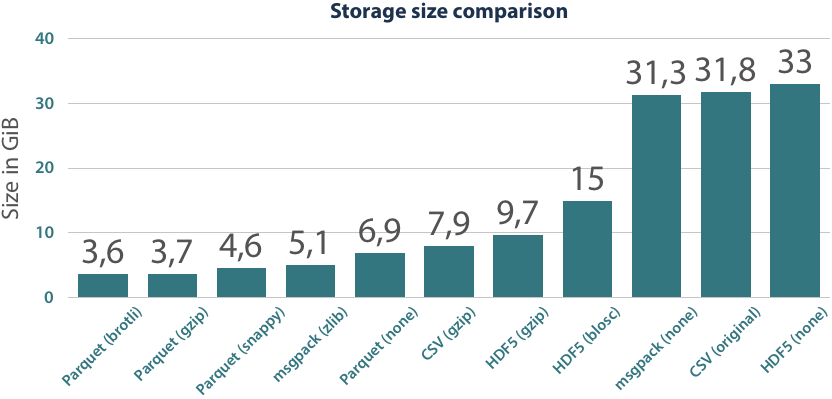
Parquet

Estructura de datos II

By Sebastian Ariza

	A	B	C	D	E	F	G
A	0	20	10	8	∞	∞	∞
B	20	0	∞	30	10	10	∞
C	10	∞	0	5	∞	∞	8
D	8	30	5	0	∞	40	20
E	∞	10	∞	∞	0	20	∞
F	∞	10	∞	40	20	0	∞
G	∞	∞	8	20	∞	∞	0

	A	B	C	D	E	F	G
A	0	20	10	8	30	30	18
B	20	0	30	28	10	10	38
C	10	30	0	5	40	40	8
D	8	28	5	0	38	38	13
E	30	10	40	38	0	20	48
F	30	10	40	38	20	0	48
G	18	38	8	13	48	48	0

	A	B	C	D	E	F	G
A	0	20	10	8	∞	∞	∞
B	20	0	∞	30	10	10	∞
C	10	∞	0	5	∞	∞	8
D	8	30	5	0	∞	40	20
E	∞	10	∞	∞	0	20	∞
F	∞	10	∞	40	20	0	∞
G	∞	∞	8	20	∞	∞	0

	A	B	C	D	E	F	G
A	0	20	10	8	30	30	18
B	20	0	30	28	10	10	38
C	10	30	0	5	40	40	8
D	8	28	5	0	38	38	13
E	30	10	40	38	0	20	48
F	30	10	40	38	20	0	48
G	18	38	8	13	48	48	0

	A	B	C	D	E	F	G
A	0	20	10	8	∞	∞	∞
B	20	0	∞	30	10	10	∞
C	10	∞	0	5	∞	∞	8
D	8	30	5	0	∞	40	20
E	∞	10	∞	∞	0	20	∞
F	∞	10	∞	40	20	0	∞
G	∞	∞	8	20	∞	∞	0

	A	B	C	D	E	F	G
A	0	20	10	8	30	30	18
B	20	0	30	28	10	10	38
C	10	30	0	5	40	40	8
D	8	28	5	0	38	38	13
E	30	10	40	38	0	20	48
F	30	10	40	38	20	0	48
G	18	38	8	13	48	48	0