What Might Machine Learning Teach Us About Human Learning?
Shayan Doroudi
March 5, 2025

That hasn't been the case for the past three decades.
My Takeaways from the History of AI and Education
Artificial intelligence (AI) research was fundamentally intertwined with education research since the early days of AI.
Normative Claim:
We should revive this interdisciplinary mode of thinking.
But what reason do we have to believe this would actually be fruitful?
Have decades of interdisciplinary research on learning resulted in any insights?
AI Has Influenced How We Think About Learning—Even If We Don't Realize It
Example:
Etymology of feedback
Cybernetics (an AI-adjacent discipline) introduced the term feedback to the social sciences.
AI Has Influenced How We Think About Learning—Even If We Don't Realize It
Another Example:
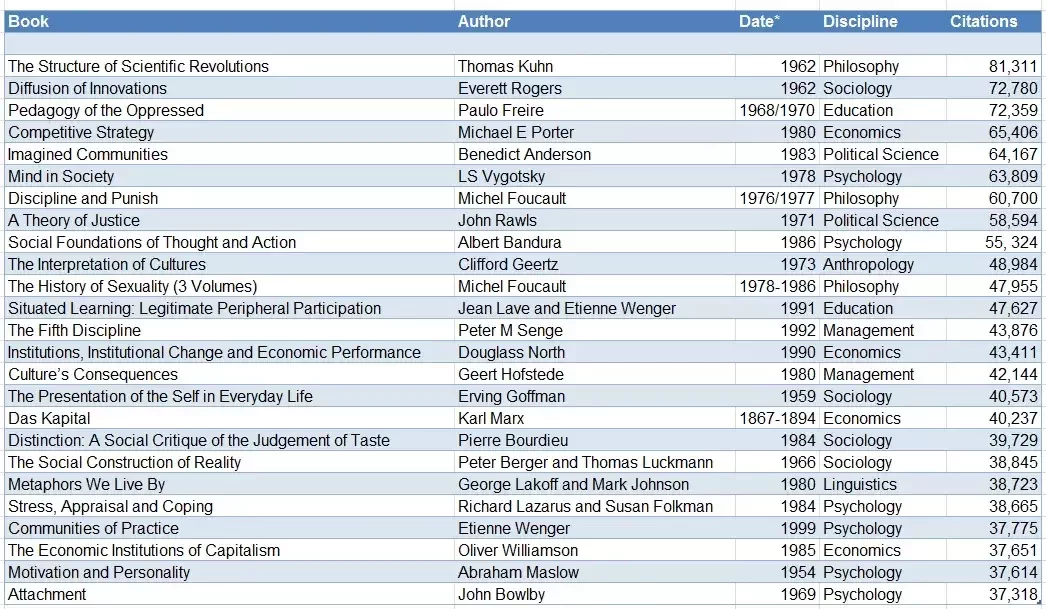
AI Has Influenced How We Think About Learning—Even If We Don't Realize It



Wenger received his PhD from Information and Computer Science at UCI!

But in what specific ways can machine learning offer insight on human learning?
Perception and Perceptrons
Case Studies
Language Learning Limits
Individual Differences in Learning and the Bias-Variance Tradeoff
Impossibility result
Possibility result
Providing an explanation for empirically observed phenomena
Perception and Perceptrons
Case Studies
Language Learning Limits
Individual Differences in Learning and the Bias-Variance Tradeoff
Chomsky (1980) claims there is a poverty of the stimulus: children are simply not exposed to enough verbal data in the environment to learn language from scratch.
Language Learning
Is our ability to learn grammar due to some innate linguistic capabilities or are we able to learn by exposure?
Chomsky (1956) characterized several different kinds of formal languages. The simplest of these is called regular languages. He also showed that regular languages are not powerful enough to express all English sentences.
Chomsky, N. (1980). Rules and representations. Behavioral and Brain Sciences, 3(1), 1-15.
Chomsky, N. (1956). Three models for the description of language. IRE Transactions on Information Theory, 2(3), 113-124.
Machine Learning Theory
Valiant (1984): Probably Approximately Correct (PAC) Learning.
To successfully be able to learn a function means to:
- Learn a reasonable approximation of the function
- In a limited* amount of time and with a limited* amount of data
- With high probability
*Limited means a polynomial function of N and some other parameters.
For example, suppose we want to learn a regular language where we keep seeing sentences of length N and are told whether the sentence belongs to the language is proper in the language or not.
Valiant, L. (1984). A theory of the learnable. Communications of the ACM, 27(11), 1134-1142.
Language Learning Limits
Are regular languages PAC-learnable?
Kearns and Valiant (1994): If regular languages are PAC-learnable, then the algorithm used to learn them can be used to break RSA cryptography!
So was Chomsky right?
The issue lies not in the amount of samples needed, but the amount of time needed! That is, there may not be a poverty of the stimulus, but a lack of time in childhood to break the linguistic code from the data we have.
Are regular languages PAC-learnable?
Kearns and Valiant (1994): If regular languages are PAC-learnable, then the algorithm used to learn them can be used to break RSA cryptography!
Possible Interpretations:
- There is a universal grammar à la Chomsky.
- There is more to language learning than seeing a bunch of examples—language learning is interactive!
- The result is only relevant in the worst case (i.e., for the most complicated languages possible)—natural languages could be much simpler.
- P = NP — a theoretical result that widely believed to be false but no computer scientist has been able to prove
- Our minds are quantum computers!
Language Learning Limits
Kearns, M., & Valiant, L. (1994). Cryptographic limitations on learning boolean formulae and finite automata. Journal of the ACM (JACM), 41(1), 67-95.
Are regular languages PAC-learnable?
Kearns and Vazirani (1994): Regular languages are PAC-learnable if we can ask questions of the form "does sentence X belong to the language?".
Possible Interpretations:
- If language learning is interactive, then language is learnable (and Chomsky was wrong)!
- But remember, this is only for regular languages. Other results suggest that formal languages closer to natural languages are not PAC-learnable under reasonable assumptions.
- Chomsky is vindicated again!
Language Learning Limits
Kearns, M. J., & Vazirani, U. (1994). An introduction to computational learning theory. MIT Press.
Perception and Perceptrons
Case Studies
Language Learning Limits
Individual Differences in Learning and the Bias-Variance Tradeoff




Perceptrons is remembered (and criticized) for being the book that halted neural network research for >15 years!
Perceptrons
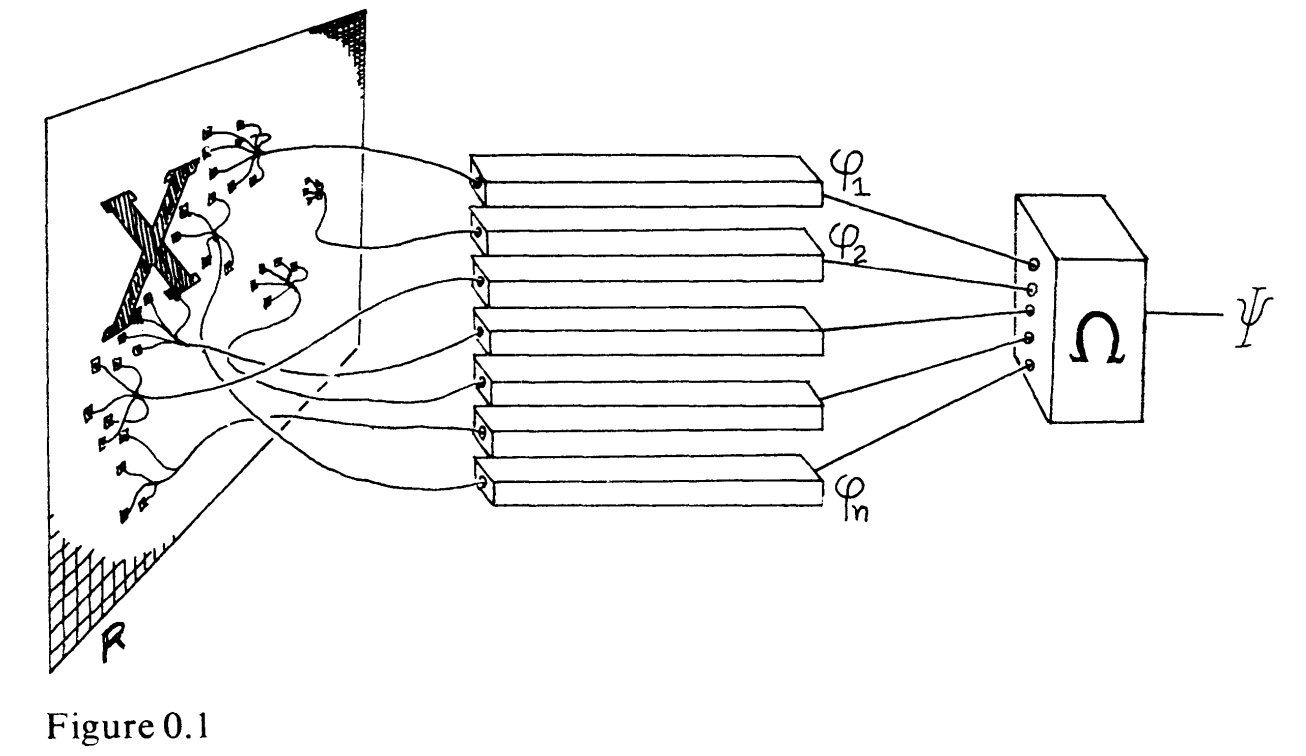
Perceptron
Minsky, M., & Papert, S. (1968). Perceptrons: An introduction to computational geometry. MIT Press.

Connectedness
Limitations of Perceptrons
Minsky and Papert (1969): No perceptron where each "neuron" has access to a small number of pixels can detect if an image is fully connected.
Minsky, M., & Papert, S. (1968). Perceptrons: An introduction to computational geometry. MIT Press.


Capabilities of Perceptrons
Minsky and Papert (1969): If an image is guaranteed to have no holes, a perceptron where each "neuron" has access to at most four pixels can detect if an image is fully connected.
This shows that there is a global property of an image that a perceptron can compute with only local evidence!
But Papert used this example in a debate with Chomsky on whether language needs to be innate!
Minsky, M., & Papert, S. (1968). Perceptrons: An introduction to computational geometry. MIT Press.
I think this result has been overlooked in the literature.




Capabilities of Human Perception?
We are not able to detect connectedness without serial processing.
Why?
- The images on the previous slides provide anecdotal evidence that connectedness without holes is easier to detect without serial processing.
- Perceptrons are the simplest kinds of artificial neural networks. If neural networks exist in our brain, surely perceptrons do!
- Perceptrons have a simple learning algorithm.
But when an image has holes, perhaps we are!
If true...
We can learn to subitize large numbers
(i.e., answer if there ≥ k objects in an image)!
We can learn to solve 2D mazes at a glance!

These possibilities are highly counter-intuitive and haven't AFAIK been conjectured before!

Copyright © 2025 Alance AB
Perception and Perceptrons
Case Studies
Language Learning Limits
Individual Differences in Learning and the Bias-Variance Tradeoff
Machine Learning
Trying to learn some function \(f\) using dataset \(D = \{(\mathbf{x_i},y_i)\}^n_{i=1} \sim \mathcal{P}_D\) where \(y_i = f(\bf{x_i})\).
We use a machine learning algorithm that selects a function \(\hat{f}\) given \(D\).

Bias
Opposite of accuracy and validity

Variance
Opposite of precision and reliability

Mean Squared Error
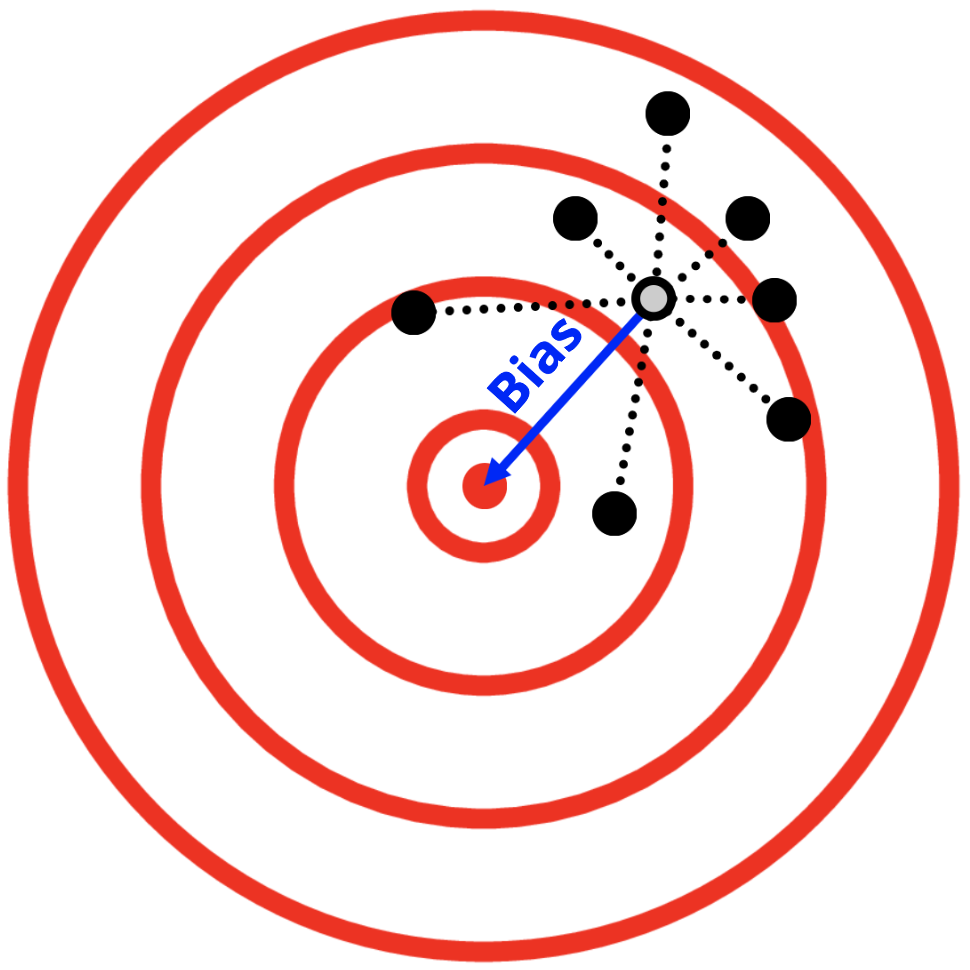

Mean Squared Error = Bias Squared + Variance
Bias-Variance Decomposition
Bias-Variance Tradeoff
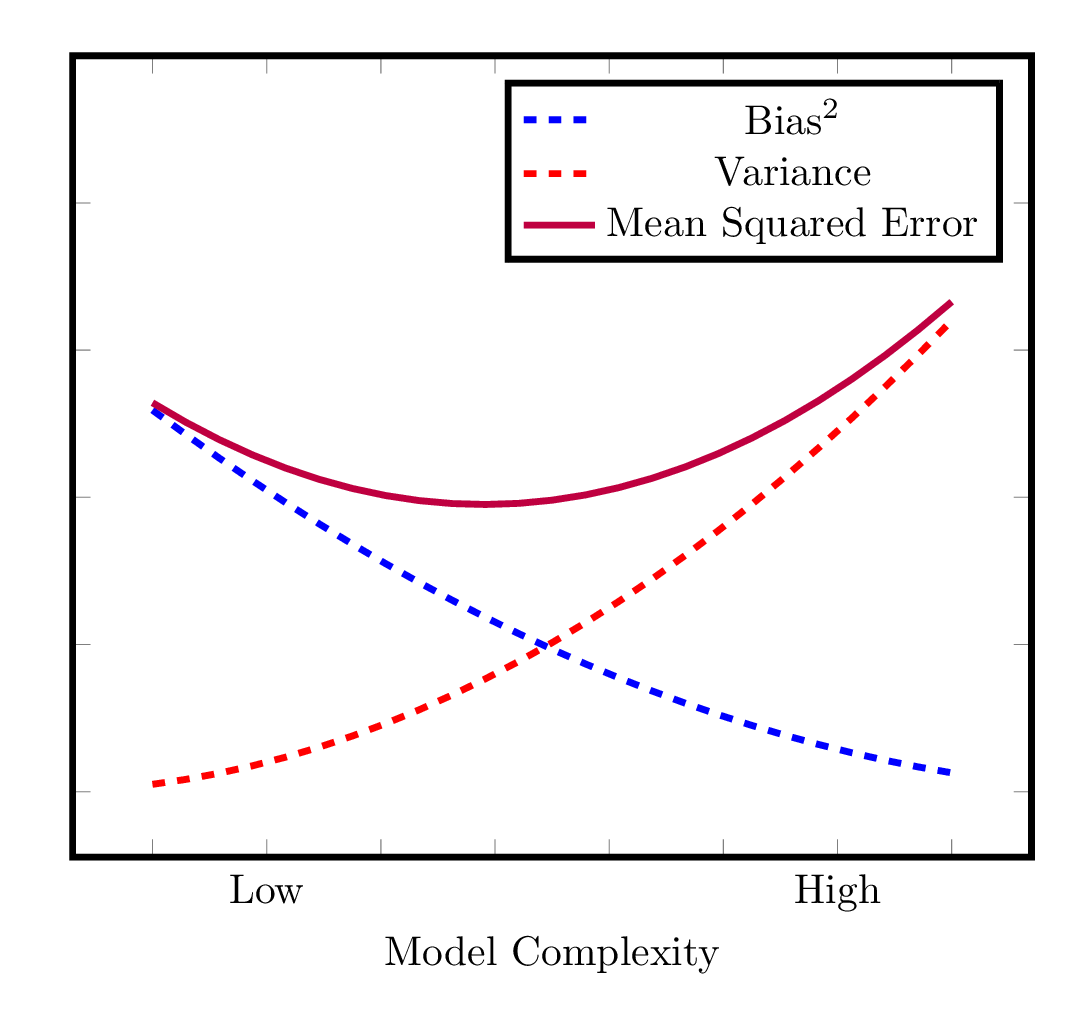
Bias-Variance Tradeoff
In order to minimize mean squared error,
some algorithms tend to minimize bias
and others tend to minimize variance.
Bias-Variance Tradeoff
In order to minimize mean squared error,
some people tend to minimize bias
and others tend to minimize variance.
Doroudi, S., & Rastegar, S. A. (2023). The bias–variance tradeoff in cognitive science. Cognitive Science, 47(1).
Doroudi, S. (2020). The bias-variance tradeoff: How data science can inform educational debates. AERA Open, 6(4), 2332858420977208.
This could potentially explain different
approaches to developing scientific theories,
teaching strategies, and
learning strategies.
Function Learning
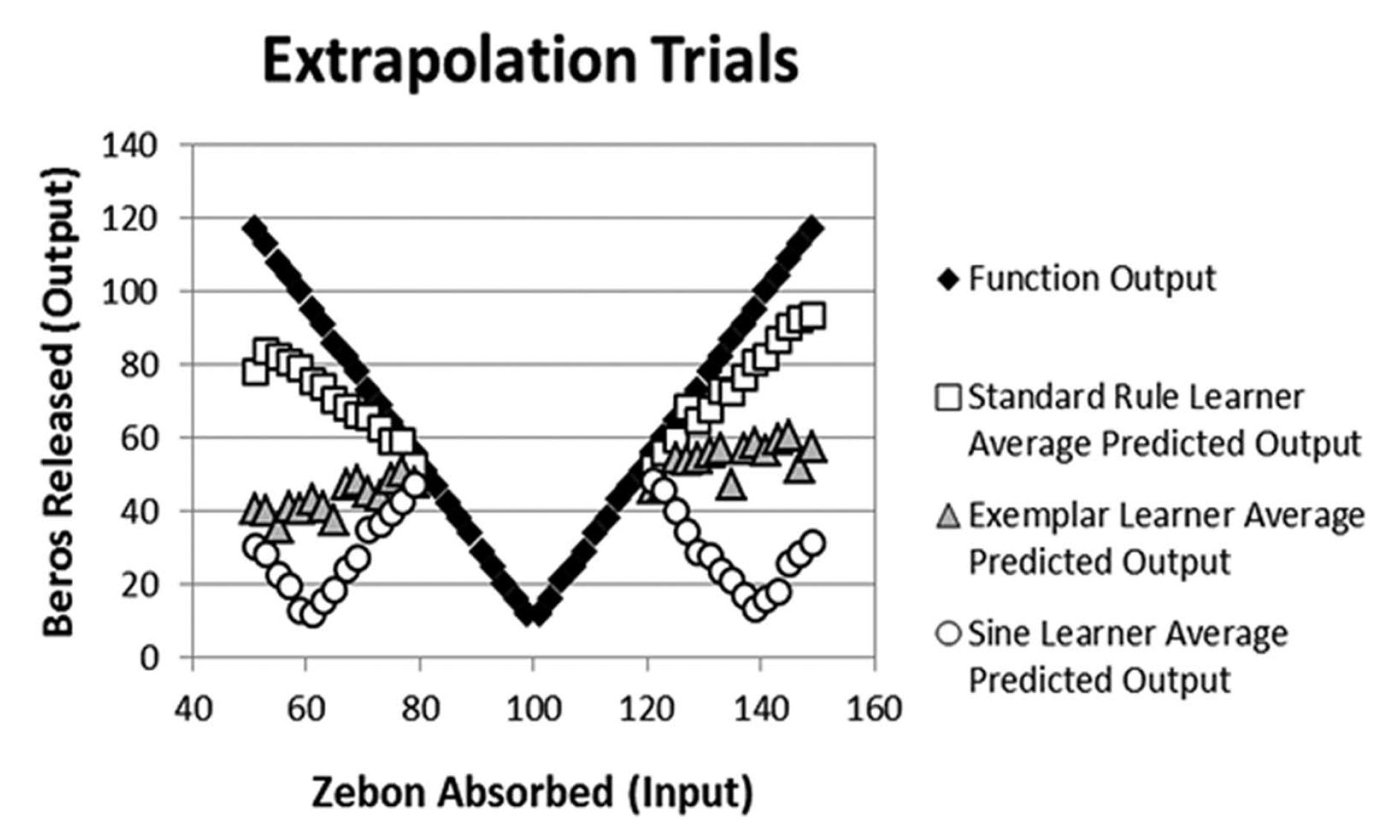
McDaniel, M. A., Cahill, M. J., Robbins, M., & Wiener, C. (2014). Individual differences in learning and transfer: stable tendencies for learning exemplars versus abstracting rules. Journal of Experimental Psychology: General, 143(2), 668.
Function Learning
McDaniel, M. A., Cahill, M. J., Robbins, M., & Wiener, C. (2014). Individual differences in learning and transfer: stable tendencies for learning exemplars versus abstracting rules. Journal of Experimental Psychology: General, 143(2), 668.

Machine learning can generate insights for human learning by:
- showing what's not possible
- showing what may be possible
- providing novel explanations for empirical results
SoE Faculty Seminar
By Shayan Doroudi
SoE Faculty Seminar
- 83



