The Bias-Variance Tradeoff
Shayan Doroudi
2020 Conference on Educational Data Science
How Data Science Can Inform Educational Debates
Data science
offers more to education than just techniques for analyzing educational data
Theoretical concepts and ideas from data science can yield broader insights to educational research.
Generalizing the Bias-Variance Tradeoff
The Bias-Variance Tradeoff in Educational Debates
Contributions
Theories of Learning
Pedagogy
Navigating the Bias-Variance Tradeoff
Outline
Background
Conclusion
Generalizing the Bias-Variance Tradeoff
The Bias-Variance Tradeoff in Educational Debates
Theories of Learning
Pedagogy
Navigating the Bias-Variance Tradeoff
Outline
Background
Conclusion
Generalizing the Bias-Variance Tradeoff
The Bias-Variance Tradeoff in Educational Debates
Theories of Learning
Pedagogy
Navigating the Bias-Variance Tradeoff
Machine Learning
Trying to learn some function \(f\) using dataset \(D = \{(\mathbf{x_i},y_i)\}^n_{i=1} \sim \mathcal{P}_D\) where \(y_i = f(\bf{x_i})\).
We use a machine learning algorithm that selects a function \(\hat{f}\) given \(D\).
\(f\)
\(\hat{f}_1\)
\(\hat{f}_2\)
\(\hat{f}_3\)
\(\hat{f}_4\)
\(\hat{f}_5\)
\(\hat{f}_6\)
\(\hat{f}_7\)
\(f\)
\(f\)
\(D_1\)
\(D_2\)
\(D_3\)
\(D_4\)
\(D_5\)
\(D_6\)
\(D_7\)
Bias
Opposite of accuracy and validity
Variance
Opposite of precision and reliability
Mean-Squared Error
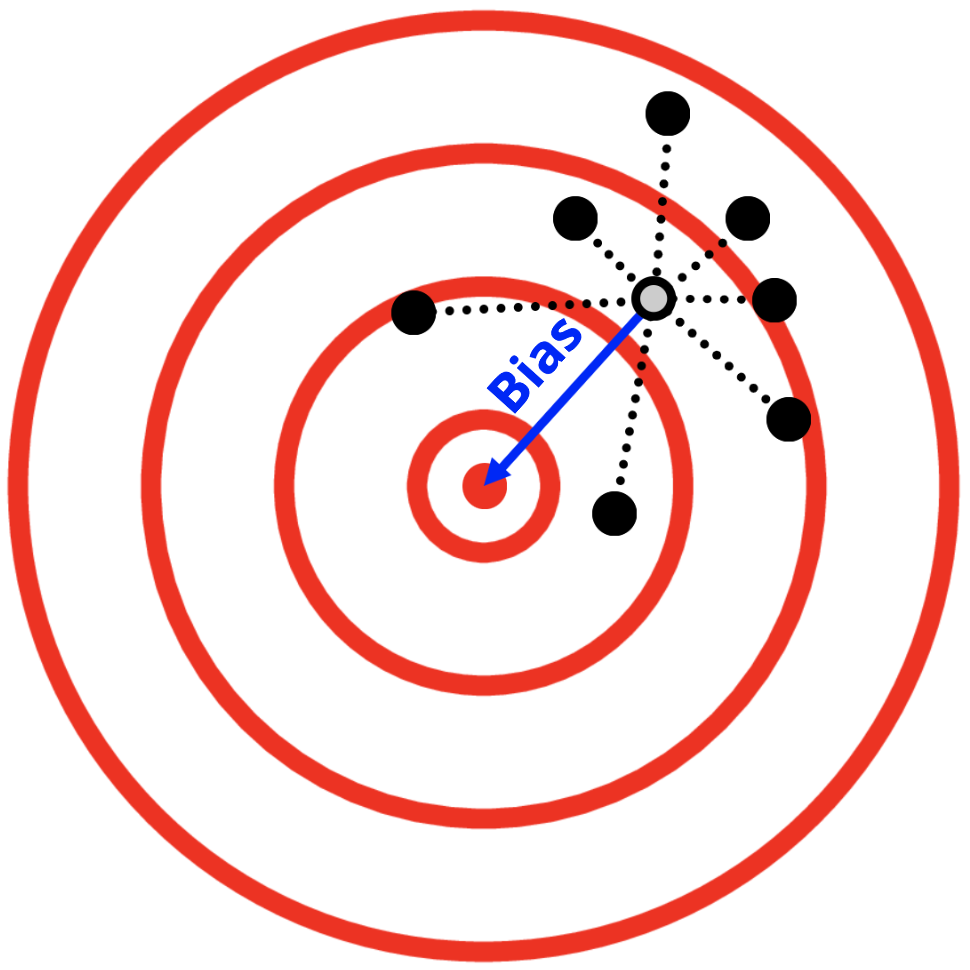
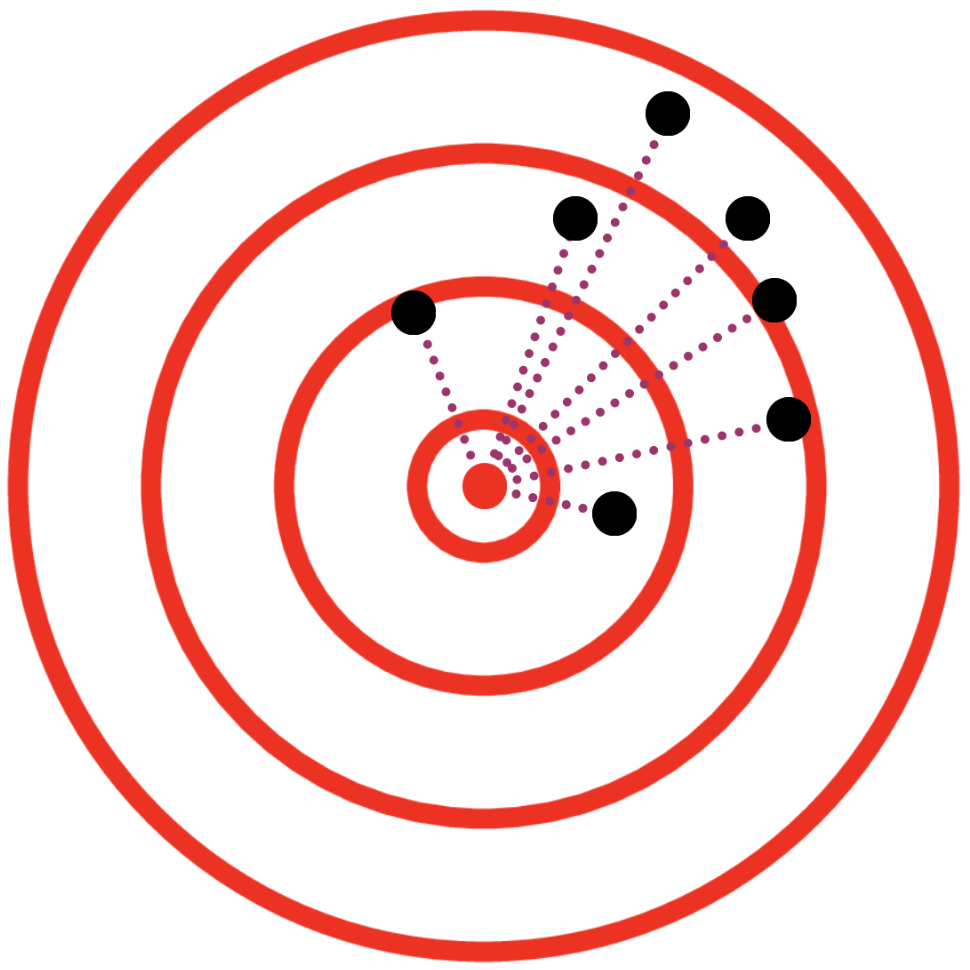
Mean-Squared Error = Bias Squared + Variance
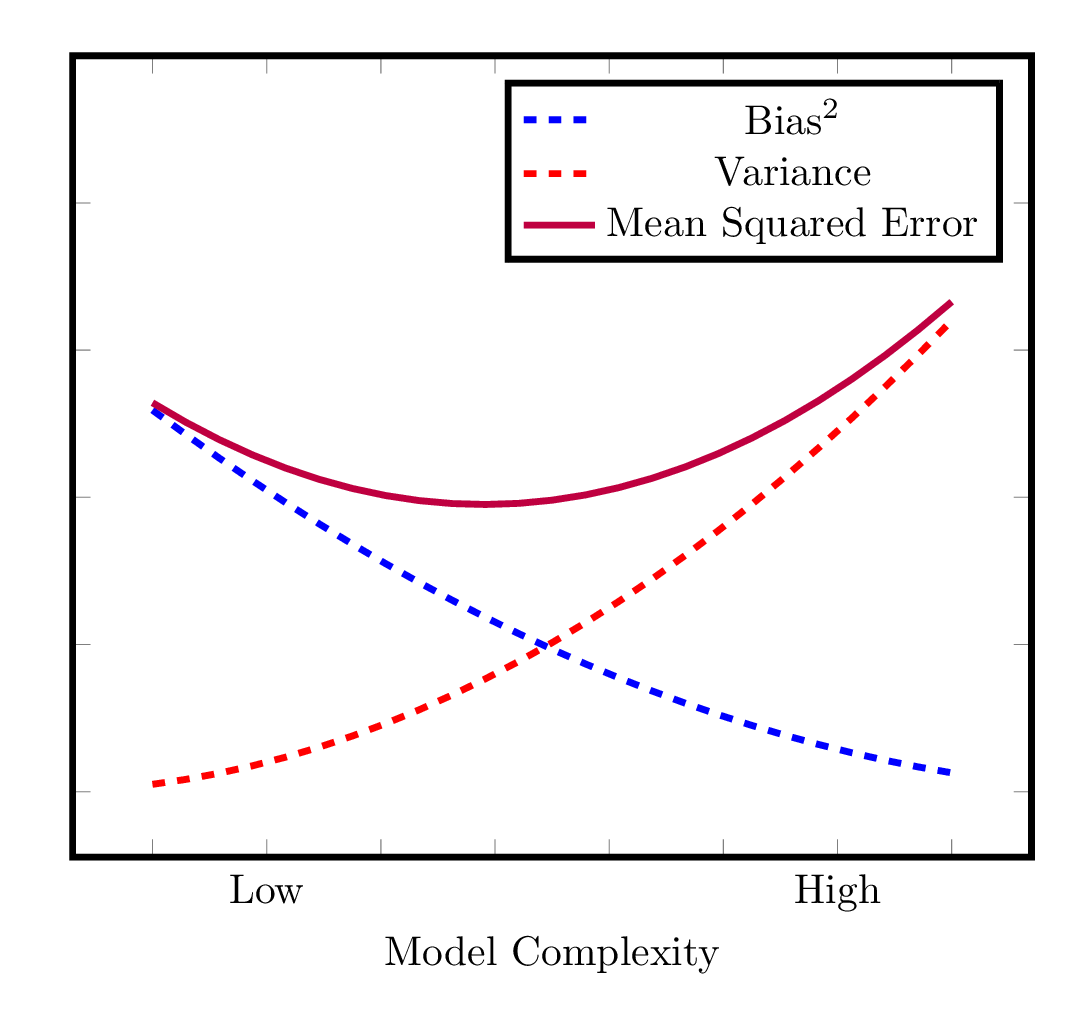
Bias-Variance Decomposition
Bias-Variance Decomposition
\underbrace{\mathbb{E}_{\mathcal{P}_D}[(\hat{f}(\mathbf{x}) - f(\mathbf{x}))^2]}_{\text{Mean-Squared Error}} = \underbrace{(\mathbb{E}_{\mathcal{P}_D}[\hat{f}(\mathbf{x})] - f(\mathbf{x}))^2}_{\text{Bias Squared}} + \underbrace{\mathbb{E}_{\mathcal{P}_D}[(\hat{f}(\mathbf{x}) - \mathbb{E}_{\mathcal{P}_D}[\hat{f}(\mathbf{x})])^2]}_{\text{Variance}}
Bias-Variance Tradeoff
Outline
Background
Conclusion
Generalizing the Bias-Variance Tradeoff
The Bias-Variance Tradeoff in Educational Debates
Theories of Learning
Pedagogy
Navigating the Bias-Variance Tradeoff
Key Observation
The bias-variance tradeoff is not really about data.
Rather, it's a property of any random mechanism that tries to approximate some target.
Generalized Bias-Variance Decomposition
\underbrace{\mathbb{E}_{\mathcal{M}}[(\hat{T}(\mathbf{x}) - T(\mathbf{x}))^2]}_{\text{Mean-Squared Error}} = \underbrace{(\mathbb{E}_{\mathcal{M}}[\hat{T}(\mathbf{x})] - T(\mathbf{x}))^2}_{\text{Bias Squared}} + \underbrace{\mathbb{E}_{\mathcal{M}}[(\hat{T}(\mathbf{x}) - \mathbb{E}_{\mathcal{M}}[\hat{T}(\mathbf{x})])^2]}_{\text{Variance}}
Let \(\mathcal{M}\) be a mechanism that randomly chooses a function \(\hat{T}\) that tries to approximate \(T\).
Goal: Approximate some target \(T : \mathbb{R}^m \rightarrow \mathbb{R}^n\)
Outline
Background
Conclusion
Generalizing the Bias-Variance Tradeoff
The Bias-Variance Tradeoff in Educational Debates
Theories of Learning
Pedagogy
Navigating the Bias-Variance Tradeoff
Outline
Background
Conclusion
Generalizing the Bias-Variance Tradeoff
The Bias-Variance Tradeoff in Educational Debates
Theories of Learning
Pedagogy
Navigating the Bias-Variance Tradeoff
Learning Theories
Cognitivism
Situativism
Constructivism
Higher variance, lower bias
Higher bias, lower variance
"Neats"
"Scruffies"
Methodology
Quantitative
Qualitative
Higher variance, lower bias
Higher bias, lower variance
Analytic / Reductionistic
Systemic / Holistic
Controlled Experiments
Design Experiments
Outline
Background
Conclusion
Generalizing the Bias-Variance Tradeoff
The Bias-Variance Tradeoff in Educational Debates
Theories of Learning
Pedagogy
Navigating the Bias-Variance Tradeoff
Pedagogy
Machine Learning
Pedagogy
Target \(T\)
Approximator \(\hat{T}\)
Mechanism \(\mathcal{M}\)
Source of Randomness
Function \(f\)
Estimator \(\hat{f}\)
ML Algorithm
\(D \sim \mathcal{P}_D\)
Optimal educational experience for each student
Actual educational experience for each student
Stochasticity in what happens during the intervention
Instructional intervention
Pedagogy
Direct Instruction
Discovery Learning
Explicitly teach students what you want them to learn
Students left to discover and construct knowledge for themselves
Rooted in cognitive theories
Rooted in constructivist theories
Pedagogy
Higher variance, lower bias
Direct Instruction
Discovery Learning
There is a wide range of possible educational experiences a student can receive.
If what you are teaching is not actually best for students, then it could be biased.
Can ensure meeting certain standardized objectives for all students.
Students may get a more authentic and personalized learning experience.
Higher bias, lower variance
Pedagogy
"Whenever children are exposed to this sort of thing, a certain number of children seem to get caught by discovering zero. Others get excited about other things.
The fact that not every child discovers zero this way reflects an essential property of the learning process. No two people follow the same path of learnings, discoveries, and revelations. You learn in the deepest way when something happens that makes you fall in love with a particular piece of knowledge"
Papert (1987):
Outline
Background
Conclusion
Generalizing the Bias-Variance Tradeoff
The Bias-Variance Tradeoff in Educational Debates
Theories of Learning
Pedagogy
Navigating the Bias-Variance Tradeoff
Navigating the Tradeoff
Increasing the Amount of "Data"
Can draw on (at least) three approaches in data science to navigate the bias-variance tradeoff:
Regularization
Model Ensembles
Increasing "DATA"
Variance decreases as the amount of data increases
(while bias does not change)
Collect more data!
What is "data" in the context of
direct instruction vs. discovery learning?
- Instructional time
Regularization
In machine learning, regularization allows us to penalize more complex functions.
Reduces overfitting at the expense of adding (hopefully little!) bias.
Guided discovery learning: teachers can add guidance to nudge (bias) students in a particular direction to avoid unproductive struggle.
Outline
Background
Conclusion
Generalizing the Bias-Variance Tradeoff
The Bias-Variance Tradeoff in Educational Debates
Theories of Learning
Pedagogy
Navigating the Bias-Variance Tradeoff
Conclusion
Theoretical constructs from data science can help us make sense of big questions that emerge in education research.
What more can data science offer education?
or vice versa?
What more can data science offer education?
and perhaps vice versa?
Learning Theories
"The alliance between situated learning and radical constructivism is somewhat peculiar, as situated learning emphasizes that knowledge is maintained in the external, social world; constructivism argues that knowledge resides in an individual’s internal state, perhaps unknowable to anyone else.
However, both schools share the general philosophical position that knowledge cannot be decomposed or decontextualized for purposes of either research or instruction."
Anderson, Reder, Simon (1996):
Learning Theories
Machine Learning
Theories of Learning
Target \(T\)
Approximator \(\hat{T}\)
Mechanism \(\mathcal{M}\)
Source of Randomness
Function \(f\)
Estimator \(\hat{f}\)
ML Algorithm
\(D \sim \mathcal{P}_D\)
True theory of learning
Proposed learning theory
Data collected from human subjects
of data
Interpretation
Educational
Data
Novel Research Findings
Adaptive Platforms
Insights for Students and Teachers
Data Science
Discussion
If pragmatic solutions exist, why do these debates still persist?
Higher variance, lower bias
Realism / Positivism
Constructivism / Interpretivism
Our understanding of the world does not necessarily correspond to an external reality
There is an external Reality and empirical observations can help us reach an objective understanding of that Reality.
Higher bias, lower variance
There are differences in epistemology.
Bias and Variance in AI
Cognitivism
Higher variance, lower bias
Higher bias, lower variance
Symbolic AI
Rule-Based AI
Asymbolic AI
Data-Driven AI
Learning Theories
Cognitivism
Situativism
Cognition and learning take place in an individual mind
Use precise computational models of cognition
Cognition and learning take place in a socio-cultural context
Use qualitative techniques to develop theories of learning
(Radical) Constructivism
Every individual constructs their own reality
Also use qualitative techniques
Learning Theories
Cognitivism
Situativism
Use precise computational models of cognition that might over-generalize how people learn.
Constructivism
A study might overfit to a particular socio-cultural context or individual but perhaps more accurate in that it models richer phenomena.
Higher variance, lower bias
Higher bias, lower variance
Learning Theories
Machine Learning
Target \(T\)
Approximator \(\hat{T}\)
Mechanism \(\mathcal{M}\)
Source of Randomness
Function \(f\)
Estimator \(\hat{f}\)
ML Algorithm
\(D \sim \mathcal{P}_D\)
True theory of learning
Proposed learning theory
Data collected from human subjects
and
of data
Interpretation
collection
Theories of Learning
Learning Theories
"We have sometimes declined to use situated language (what Patel, 1992, called “situa-babel”) because we do not find it a precise vehicle for what we want to say. In reading the literature of situated learning, we often experience difficulty in finding consistent and objective definitions of key terms."
Anderson, Reder, Simon (1997):
Learning Theories
"One of our students at MIT, Robert Lawler, wrote a Ph.D. thesis years ago based on his observation of a six-year-old child. Over a period of six months, he observed this child almost continuously, never missing as much as a half hour. . . . When people study the learning process, they usually study a hundred children for several hours each, and Lawler showed very conclusively . . . that you lose a lot of very important information that way. By being around all the time, he saw things with this child that he certainly would never have caught from occasional samplings in the laboratory."
Papert (1987):
Cognitivism
Higher variance, lower bias
Higher bias, lower variance
"Neats"
"Scruffies"
Situativism
Constructivism
Bias and Variance in AI
Simon, Newell, Anderson
Papert, Minsky, Schank
Symbolic AI
Rule-Based AI
Cognitivism
Higher variance, lower bias
Higher bias, lower variance
Situativism
Constructivism
Bias and Variance in AI
"While neats focused on the way isolated components of cognition worked, scruffies hoped to uncover the interactions between those components."
Kolodner (2002):
"Neats"
"Scruffies"
Bias and Variance in Machine learning
Linear Models
Deep
Neural Networks
Higher variance, lower bias
Higher bias, lower variance
Random
Forests
Polynomial
Regression
Hypothetical Debate
Position 1
Position 2
High-Level Description of Position 1
High-Level Description of Position 2
Machine Learning
Hypothetical Debate
Target \(T\)
Approximator \(\hat{T}\)
Mechanism \(\mathcal{M}\)
Source of Randomness
Function \(f\)
Estimator \(\hat{f}\)
ML Algorithm
\(D \sim \mathcal{P}_D\)
...
...
...
...
Hypothetical Debate
Hypothetical Debate
High-level explanation of why Position 1 has higher bias but lower variance.
High-level explanation of why Position 2 exhibits higher variance but lower bias.
Position 1
Position 2
Hypothetical Debate
Historical quotes from learning scientists that give evidence for why one position might be seen as having higher bias or variance than the other.
Lower Bias
Lower Bias
and Variance
Model ensembles
Model ensemble learning combines multiple models to create an aggregate model that has less bias and/or variance than the individual models.
Can draw inspiration from Papert's "microworlds."
Model Ensembles
Model ensemble learning combines multiple models to create an aggregate model that has less bias and/or variance than the individual models.
Each model—or “micro-world” as we shall call it—is very schematic. . .we talk about a fairyland in which things are so simplified that almost every statement about them would be literally false if asserted about the real world. Nevertheless, we feel they are so important that we plan to assign a large portion of our effort to developing a collection of these micro-worlds and finding how to embed their suggestive and predictive powers in larger systems without being misled by their incompatibility with literal truth.
Minsky and Papert (1971):
Model Ensembles
So, we design microworlds that exemplify not only the “correct” Newtonian ideas, but many others as well: the historically and psychologically important Aristotelian ones, the more complex Einsteinian ones, and even a “generalized law-of-motion world” that acts as a framework for an infinite variety of laws of motion that individuals can invent for themselves. Thus learners can progress from Aristotle to Newton and even to Einstein via as many intermediate worlds as they wish.
Model ensemble learning combines multiple models to create an aggregate model that has less bias and/or variance than the individual models.
Papert (1980):
Model Ensembles
probably in all important learning, an essential and central mechanism is to confine yourself to a little piece of reality that is simple enough to understand. It’s by looking at little slices of reality at a time that you learn to understand the greater complexities of the whole world, the macroworld. (p. 81)
Papert (1987):
Model ensemble learning combines multiple models to create an aggregate model that has less bias and/or variance than the individual models.
Archery is not data-driven!
Stanford EDS 2020
By Shayan Doroudi
