[video edited from 3b1b]

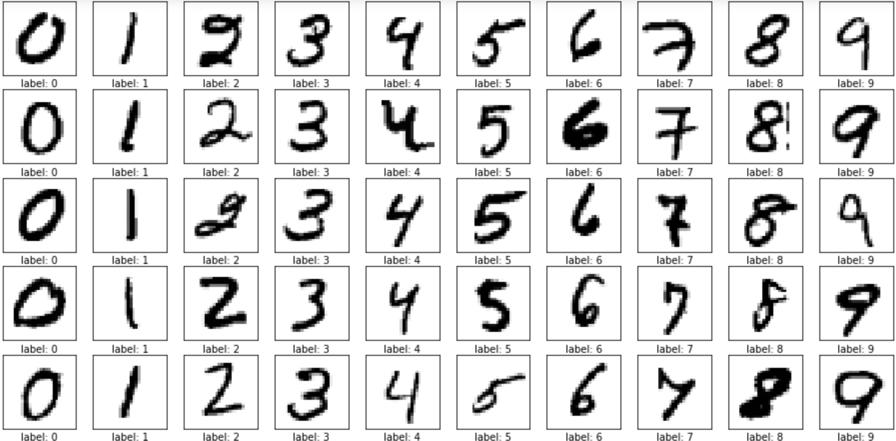
Consider the MNIST dataset

[video edited from 3b1b]

trained such a 2-hidden-layer network for classification

Training Accuracy 97%

Testing Accuracy 81%

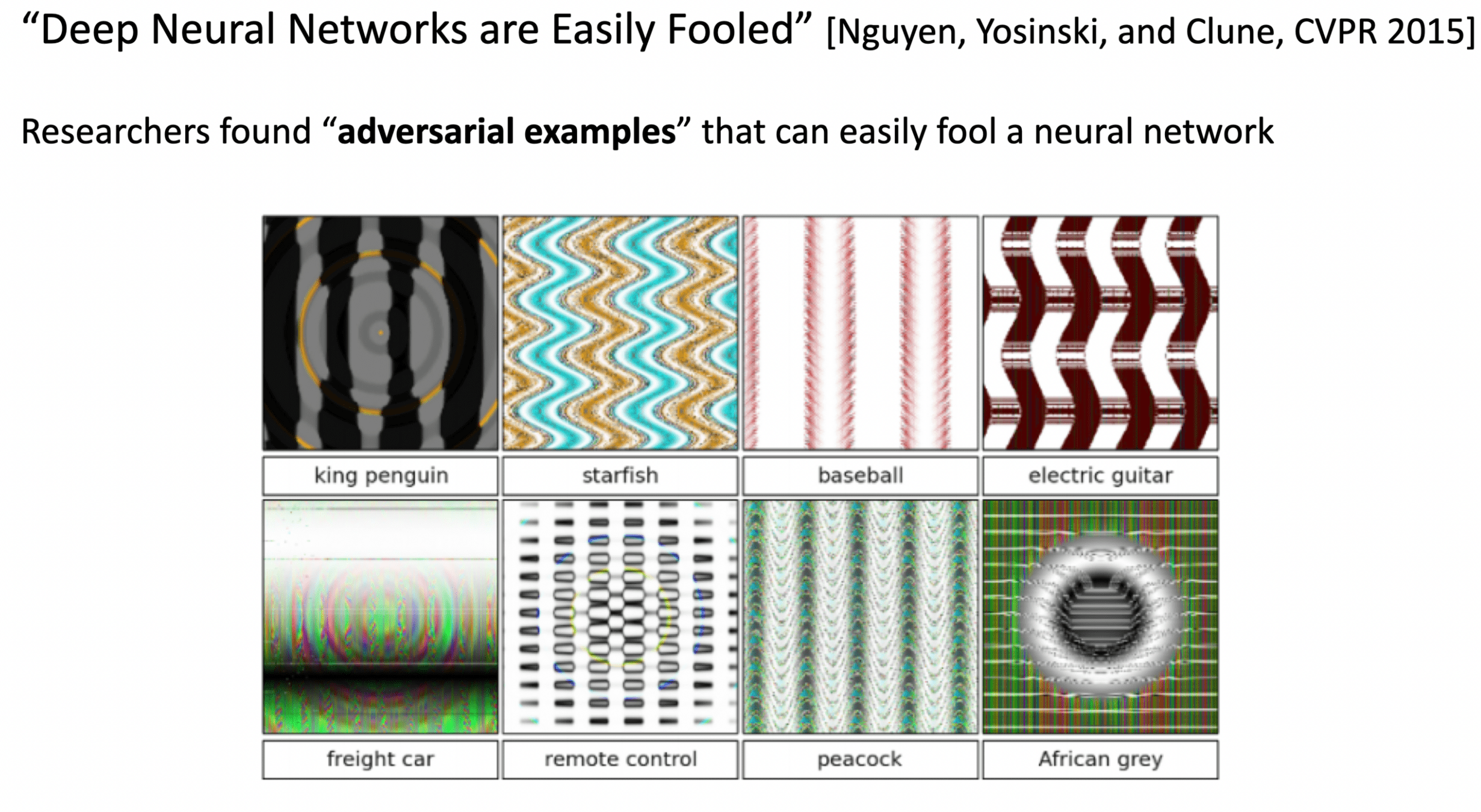
The canonical ____ ?

overfitting

...

trained such a 2-hidden-layer network for classification

Training Accuracy 97%

Testing Accuracy 60%

...

The canonical domain shift

Is this overfitting?

Does this performance gap "feel" the same as before?

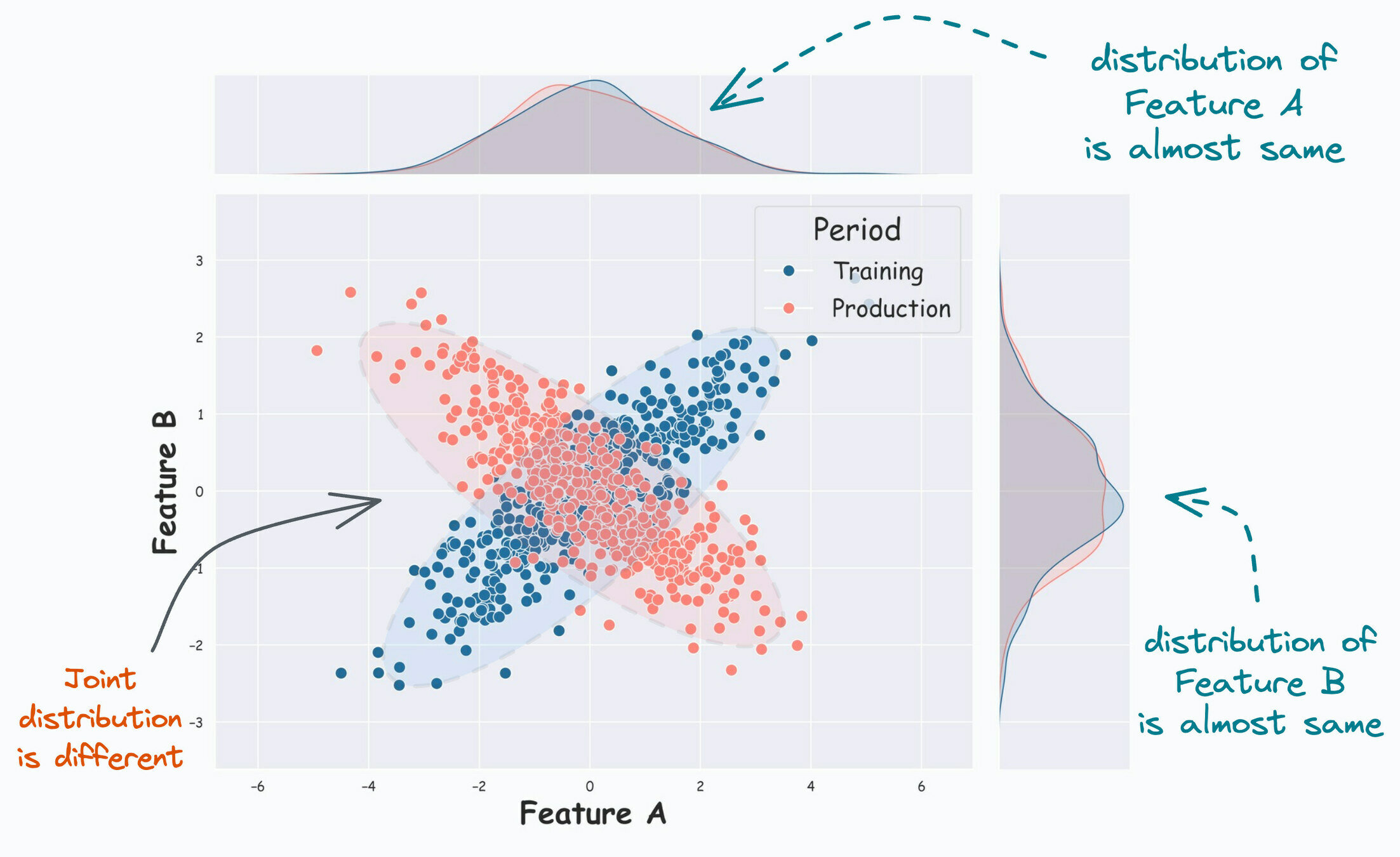
We usually assume that the data we use to train a model is representative of what it will see in the real world — i.e., training and test data share the same structure and characteristics.

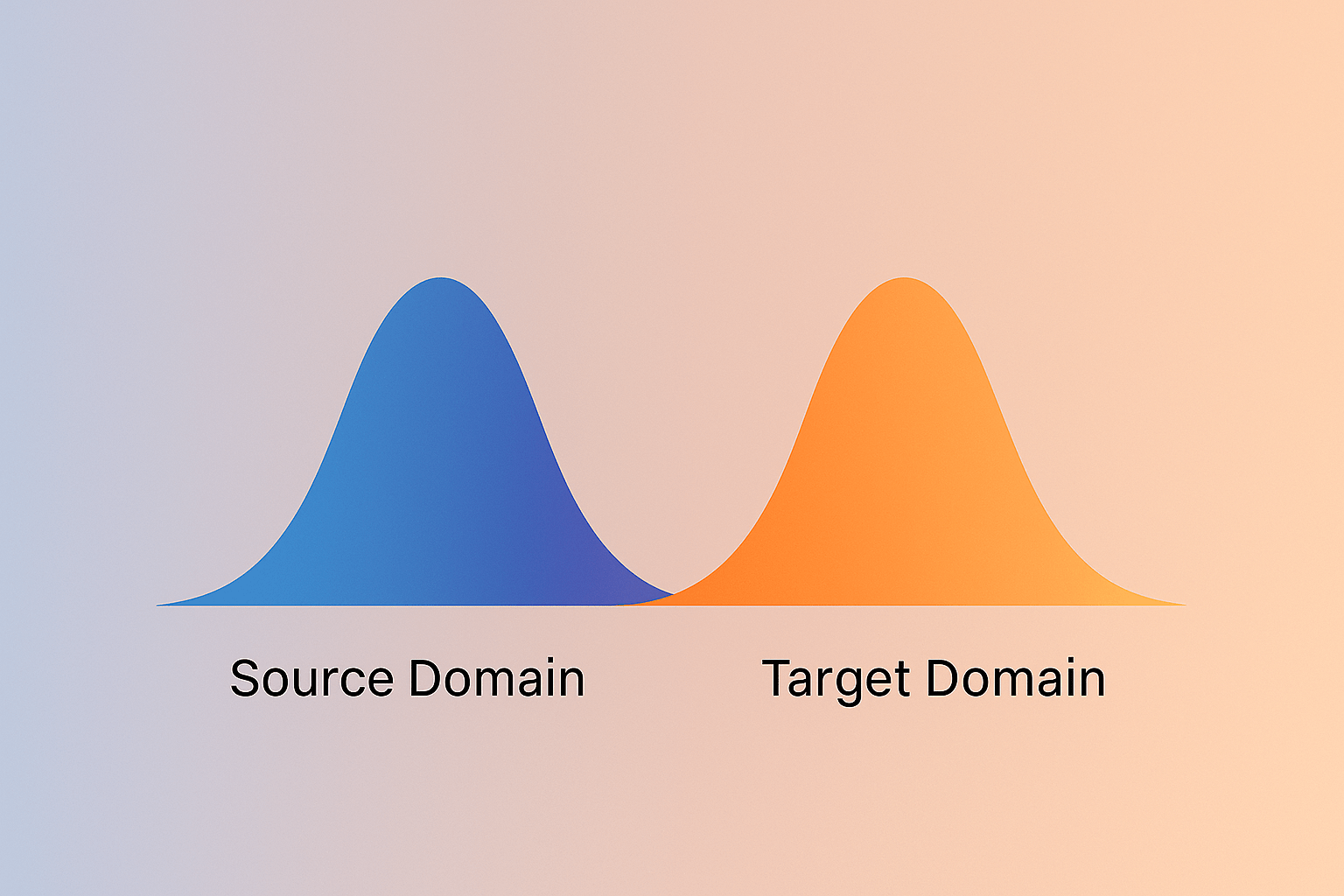
What is domain shift?

same domain

different domains

In other words, we often assume training and test data come from the same distribution, or the same domain. Domain shift happens when this assumption fails.

	Overfitting	Domain Shift
Training vs. Testing Error	Training low, testing high
Analogy	studies only past C01 exams, tested on C01 exam	studies all C01 materials (hw, lectures, etc.), tested on C011 exam
Cause	Model memorizes noise or overly specific patterns	Distribution mismatch between training and testing data
Symptoms	High variance across data splits	Poor generalization on new environments or populations
Data Distribution	Same for train and test (P_train(x, y) ≈ P_test(x, y))	Different for train and test (P_train(x, y) ≠ P_test(x, y))
Typical Fixes	Regularization, dropout, simpler model, more data	Domain adaptation, importance weighting, data augmentation

ML models may generalize poorly when domain shift occurs.

Domain Shift Is the Norm, Not the Exception

E.g., temporal changes:

predictors trained from older data before Covid
applied post Covid

E.g., demographic/context changes

speech recognition system

trained on 🇬🇧 accent

applied on 🇬🇧 🇮🇪 🇺🇸 🇦🇺 ... accents

E.g., demographic/context changes
- risk predictors that are trained on patient data from one hospital and used in a different hospital

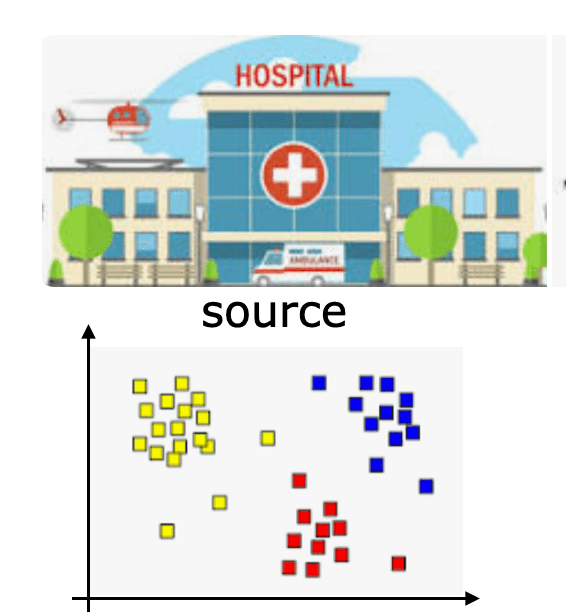
trained at

deployed at

we also call this the

source

and this the target

E.g., actions we take

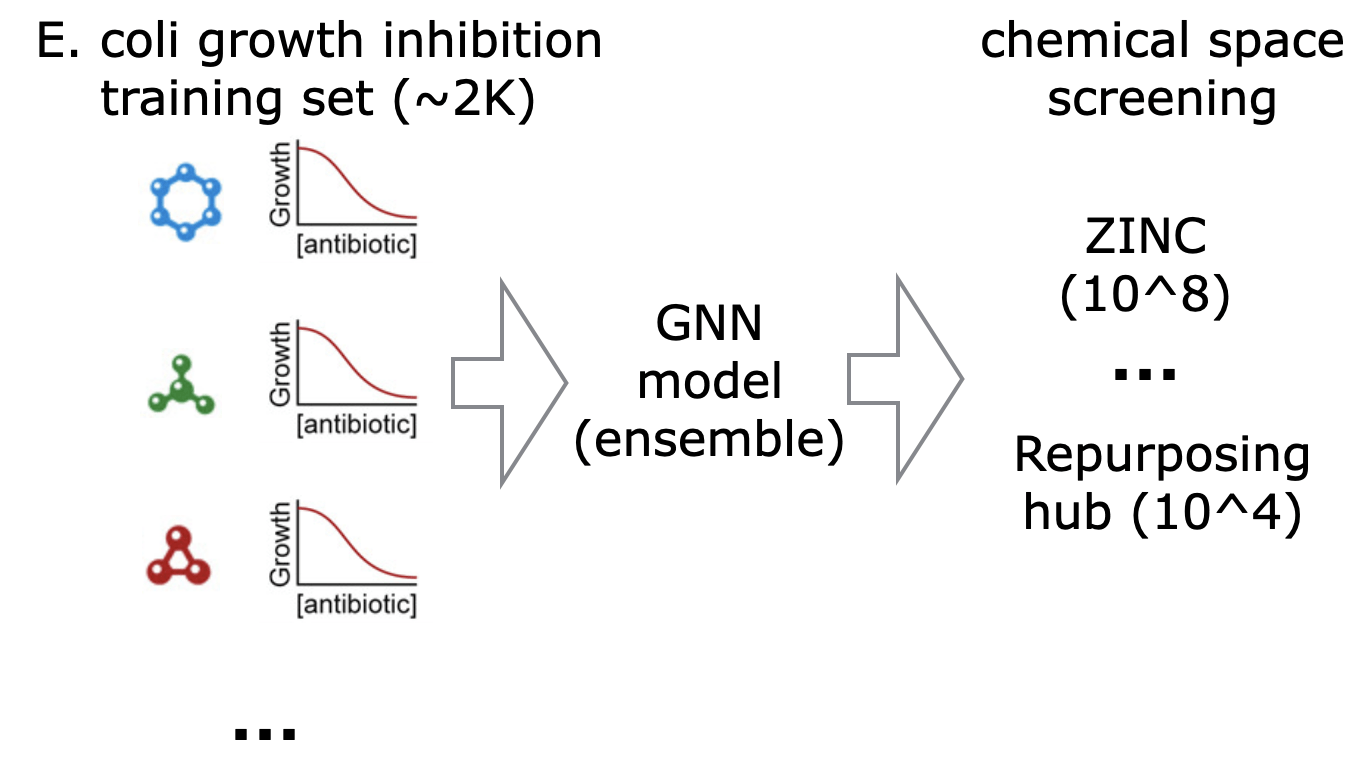
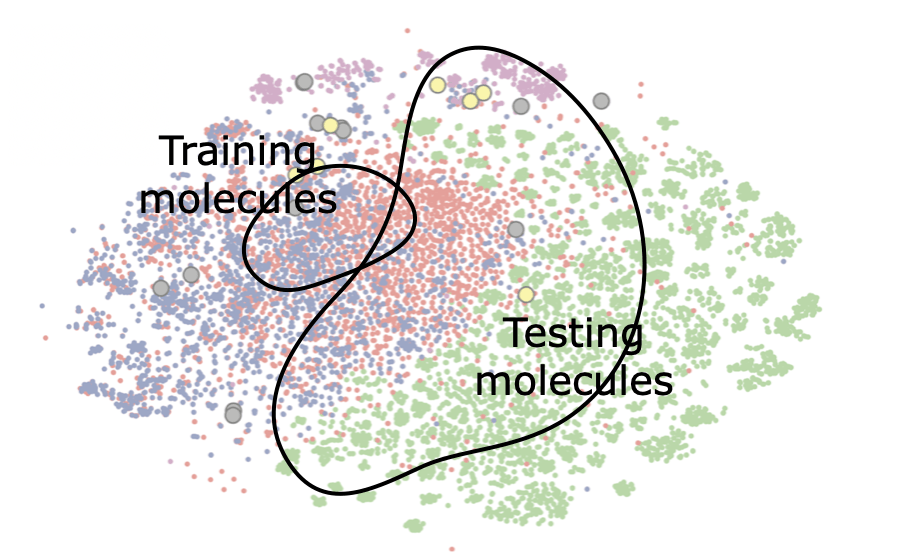
predictors that are used in iterative experiment design (e.g., molecule optimization) where the current data comes from earlier rounds of selections

E.g., wildlife species predictor, class distribution is different for each static sensor location

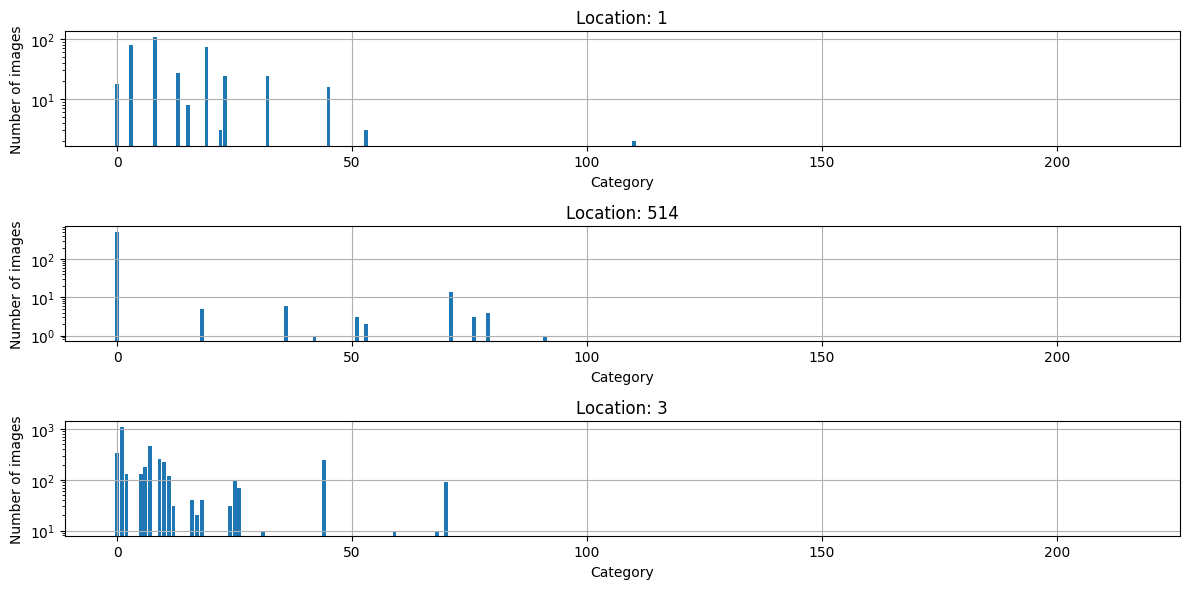
E.g., wildlife species predictor, class distribution is different for each static sensor location

Performance can be substantially affected by “domain shift”…

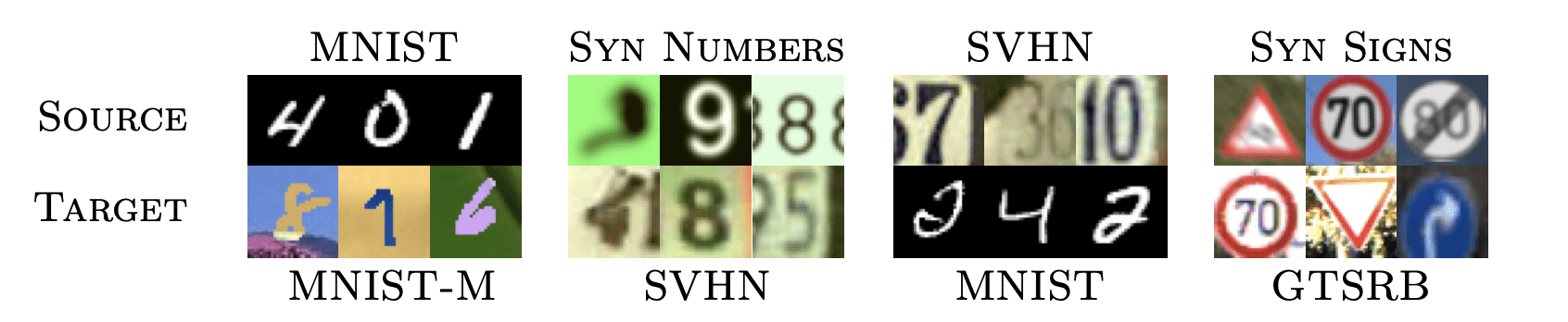
[Ganin et al. 2015]

[Koh et al. 2021]

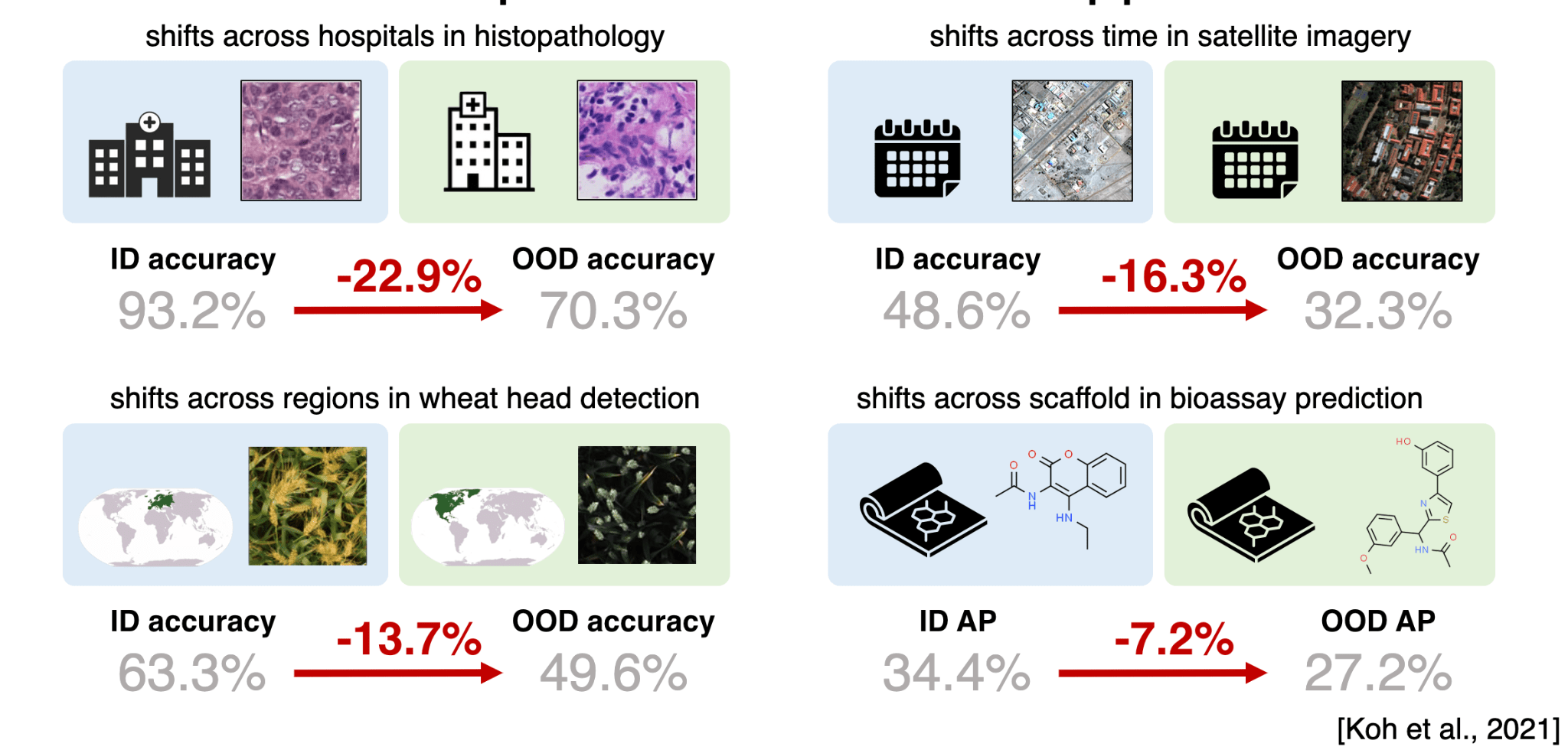
Performance can be substantially affected by "domain shift"…

[Beery et al. 2020, Koh et al. 2021]

Performance can be substantially affected by "domain shift"…

Nowadays, in the pre-training scenario, both data and task are typically different between the source (pre-training data/task) and the target (our actual task/data)
For the rest of the lecture we focus on understanding and adjusting to “data shifts” while the prediction task remains the same
The differences in the data arise for many reasons, and these reasons may be known or unknown
We'd rely on domain adaptation to deal with the shift.

Domain Shift

very little one can do when the shift is "too significant".

to deal with shift in a meaningful way, there must be some properties -- maybe hidden, or conditional -- that remain unchanged, despite the overall shift

How to address domain shift?

e.g. if the target task is to speak a foreign language, it seems almost useless to train on skateboarding

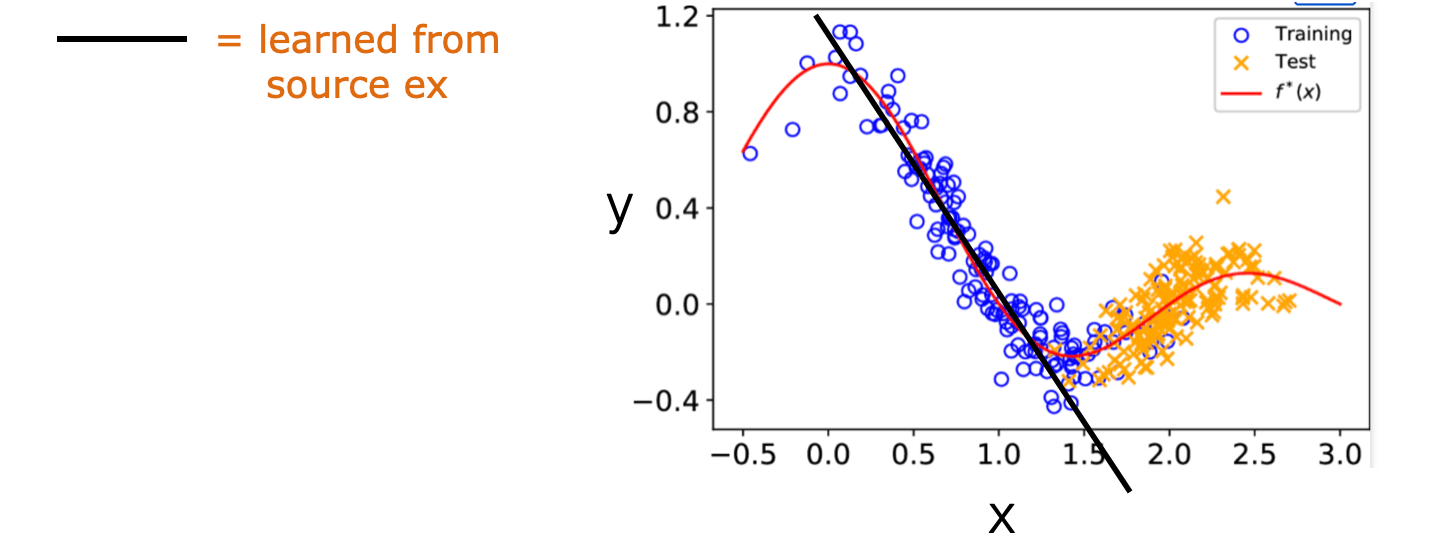
E.g. Train a deer detector using images (captured in sunny daytime)

What's the features, what's the label?

Train a deer detector using images (captured in sunny daytime)

Deployed in nighttime ...

A deer detector, trained in daytime and tested in nighttime:

Q: What's changing?
A: The feature \(x\) daytime is brighter, more blues and greens. nighttime more blacks and yellows

Q: What must remain the same for the training to have some hope of being "meaningful"?
A: What a deer looks like, regardless of the color, must retain a deer-ish 🦌 silhouette

A deer detector, trained in daytime and tested in nighttime:

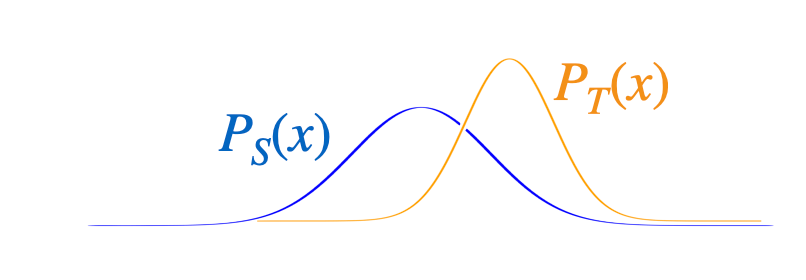
The defining characteristic of co-variate shift, i.e., that the target \(P_T(x)\) differs from the source \(P_S(x)\), is present in almost any real prediction task
There's an additional assumption that the relation between \(x\) and \(y\) remains the same; this assumption is less often true in reality (but enables us to do something)
The effect is that, e.g., estimating a regression model from the source data may improperly emphasize the wrong examples (never seen in target domain)

Case # 1 Co-variate Shift

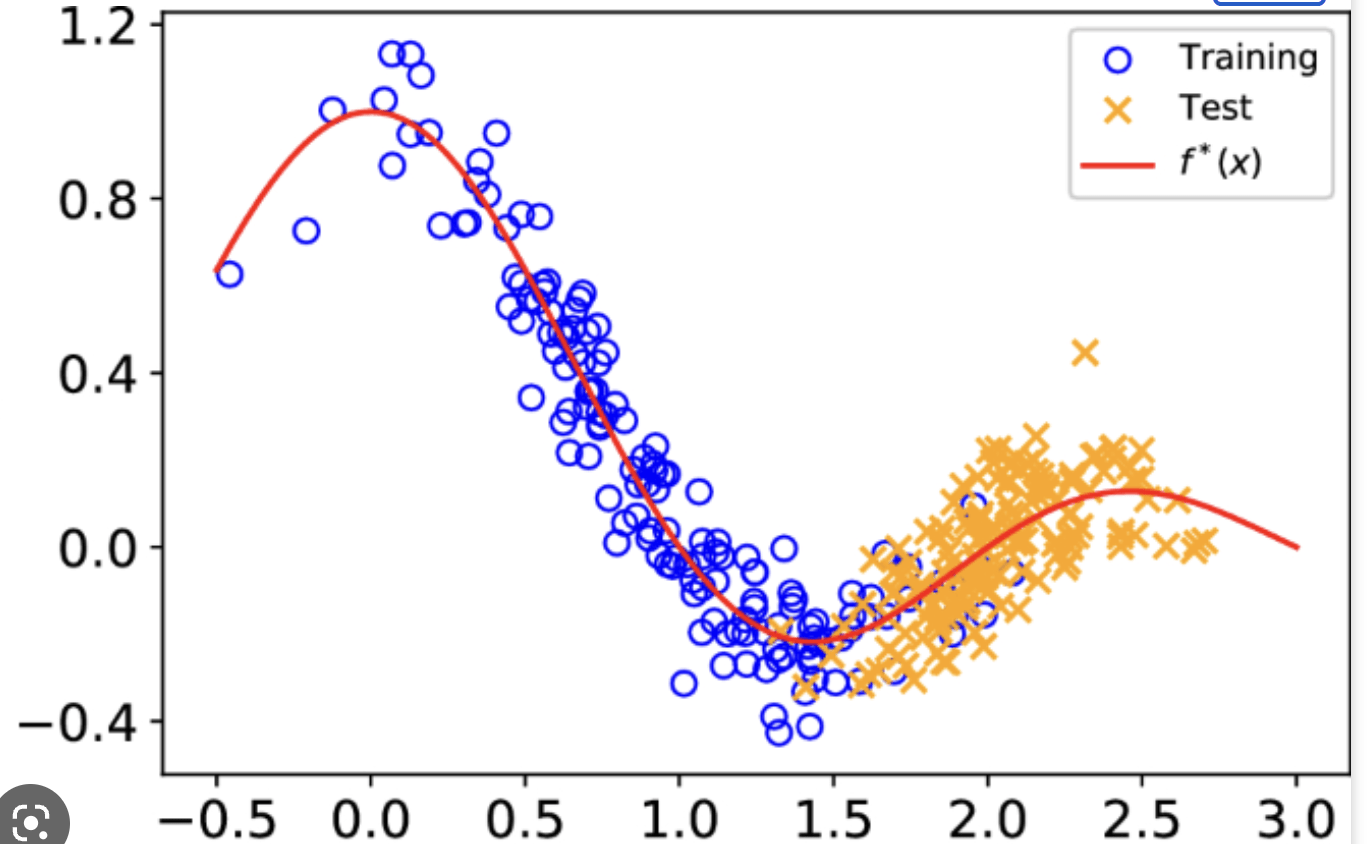
The effect of co-variate shift is that, e.g., estimating a regression model from the source data may improperly emphasize the wrong examples
Assumptions:
- common underlying function or \(P(y \mid x)\)
- lots of labeled examples from the source
- lots of unlabeled examples from the source and the target
We want:
- a \(P(y \mid x)\) estimate that works well on the target samples

Case # 1 Co-variate Shift

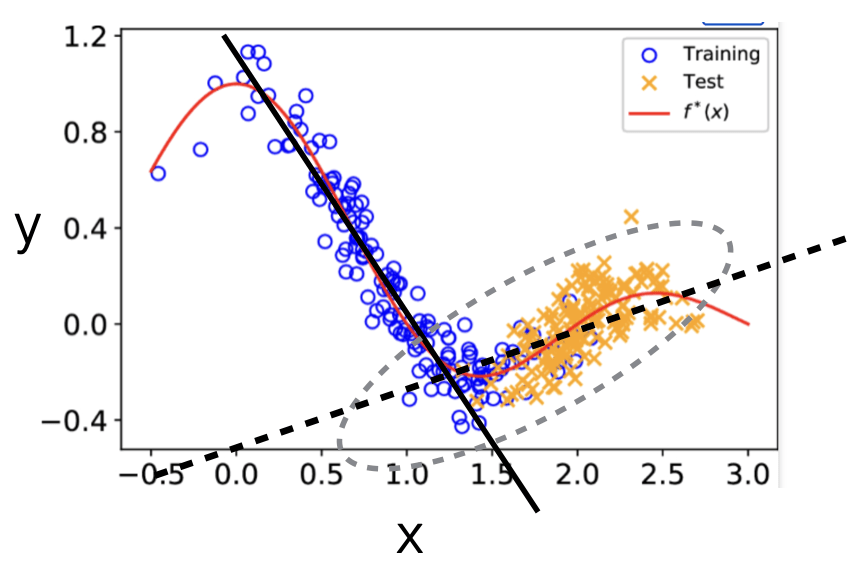
When \(P_T(x)\) differs from \(P_S(x)\) we could still in principle use the same classifier or regression model \(P(y \mid x, \theta)\) trained from the source examples
But estimating this regression model from the source data may improperly emphasize the wrong examples (e.g., x 's where \(P_S(x)\) is large but \(P_T(x)\) is small)

Case # 1 Co-variate Shift

We would like to estimate \(\theta\) that minimizes

\(\sum_{x, y} P_T(x, y) \operatorname{Loss}(x, y, \theta)\)

\(=\sum_{x, y} P_S(x, y) \frac{P_T(x, y)}{P_S(x, y)} \operatorname{Loss}(x, y, \theta)\)

\(=\sum_{x, y} P_S(x, y) \frac{P_T(x) P_T(y \mid x)}{P_S(x) P_S(y \mid x)} \operatorname{Loss}(x, y, \theta)\)

\(=\sum_{x, y} P_S(x, y) \frac{P_T(x)}{P_S(x)} \operatorname{Loss}(x, y, \theta)\)

average over the target distribution

weighted average over the source distribution

Case # 1 Co-variate Shift

How do we get the ratio \(P_T(x) / P_S(x)\) used as weights in the new estimation criterion? If \(x\) is high dimensional, estimating such distributions is challenging.
It turns out we can train a simple domain classifier to estimate this ratio
- only use unlabeled examples from the source and target
- label examples according to whether they come from the source S or target T
- estimate a domain classifier \(Q(S \mid x)\) from such labeled data
If the domain classifier is "perfect" then

\(Q(S \mid x)=\frac{P_S(x)}{P_S(x)+P_T(x)} \quad \frac{Q(S \mid x)}{Q(T \mid x)}=\frac{P_S(x)}{P_T(x)}\)
So we can get the ratio weights required for estimation directly from the domain classifier

Case # 1 Co-variate Shift

Since we can now get the required probability ratios from the domain classifier, we can estimate

\begin{align*} \sum_{x,y} P_T(x,y) \,\text{Loss}(x,y,\theta) &= \sum_{x,y} P_S(x,y) \frac{P_T(x)}{P_S(x)} \,\text{Loss}(x,y,\theta) \\ &= \sum_{x,y} P_S(x,y) \frac{Q(T|x)}{Q(S|x)} \,\text{Loss}(x,y,\theta) \\ &\approx \frac{1}{n}\sum_{i=1}^n \frac{Q(T|x^i)}{Q(S|x^i)} \,\text{Loss}(x^i,y^i,\theta) \end{align*}

The labeled samples are now source training examples. The domain classifier itself is estimated from unlabeled source and target samples (co-variates only)

Case # 1 Co-variate Shift

Now let's look at another type of shift that's "fixable" in a relatively easy and principled way

TODO: so many bugs... 😱

need fix

Similar to the MNIST demo, consider a similar scenario.

A species detector, trained using images from location 514.

What's the features, what's the labels?

Features \(x\): images, labels \(y\): category index

Species detector, trained at location 514, deployed at other locations.

What are do these bar charts represent?

Distribution over \(y:\) e.g. species 25 rare at location 514, not so rare at other locations.

[image source]

Here, we adjust an already trained classifier \(P_S(y \mid x)\) so that it is appropriate for the target domain where the label proportions are different
E.g., a new specialized clinic appears next to a hospital. So patients with certain illnesses covered by the clinic are now less frequently coming to the hospital. But we can hypothesize that those who still come “look” the same as before, there are just fewer of them.

Case # 2 Label shift

More formally, assumptions:

Lots of source examples, can train an optimal source classifier \(P_S(y \mid x)\)
Labeled examples look conditionally the same from source to target, i.e., \(P_S(x \mid y)=P_T(x \mid y)\), but proportions of different labels change
We know the label proportions \(P_S(y)\) (observed) and \(P_T(y)\) (assumed)

We want:

optimal target classifier \(P_T(y \mid x)\)

Case # 2 Label shift

how we can adjust an already trained classifier \(P_S(y \mid x)\) so that it is appropriate for the target domain where the label proportions are different
Let's consider any \(x\) (fixed, only y varies) and try to construct the target classifier based on the available information

Adjusting for label shift

\(P_T(y \mid x) \propto P_T(x \mid y) P_T(y)\)

\(=P_S(x \mid y) P_T(y)\)

\(=P_S(x \mid y) P_S(y) \frac{P_T(y)}{P_S(y)}\)

\(\propto \frac{P_S(x \mid y) P_S(y)}{P_S(x)} \frac{P_T(y)}{P_S(y)}\)

\(=P_S(y \mid x) \frac{P_T(y)}{P_S(y)}\)

class conditional distributions assumed to be the same

x is fixed, so we can include any x term

we have expressed the target classifier proportionally to the source classifier and the label ratios; normalizing this across y for any given x gives our target classifier

Let’s consider two scenarios where we can adjust what we do

Case #1 (label shift only): the proportions of labels differs from the source to the target domain, the data are otherwise generated the same
Case #2 (co-variate shift only): the distribution of co-variates (distribution over x’s) differs from the source to target domain, the data are otherwise generated the same

(these are not mutually consistent, and do not cover all shifts)

Adjusting for two types of shifts

Domain Shift and Adaptation Summary

Shift Type	What Changes?	Typical Assumption	Need to Reweight?	Need to Relearn?
Covariate Shift	P(x) changes	P(y\|x) stays the same	Yes (importance sampling on x)	No
Label Shift	P(y) changes	P(x\|y) stays the same	Yes (importance sampling on y)	No
Concept Shift	P(y\|x) changes	Neither P(x) nor P(y) necessarily stay the same	No (reweighting not enough)	Yes

More general domain adaptation possibilities

Goal is to learn from labeled/annotated training (source) examples and transfer this knowledge for use in a different (target) domain
For supervised learning: we have some annotated examples also from the target domain
For semi-supervised: we have lots of unlabeled target examples and just a few annotations
For unsupervised: we only have unlabeled examples from the target domain
For reinforcement learning: we have access to (source) environment, and aim to transfer policies to a (target) environment, possibly with limited or no interaction data from the target

ToDo: add citations, plots here for each case

Data augmentation

Common problem: I collect all my data in Spring, but the model does not work anymore in Winter!
Possible solutions:
- Add augmentation to account for distribution shift, e.g., color jittering
- Use pre-trained model that has been trained on all-season data, though not exactly your task
- Or… just wait for Winter and collect more data (most effective)!

Domain randomization

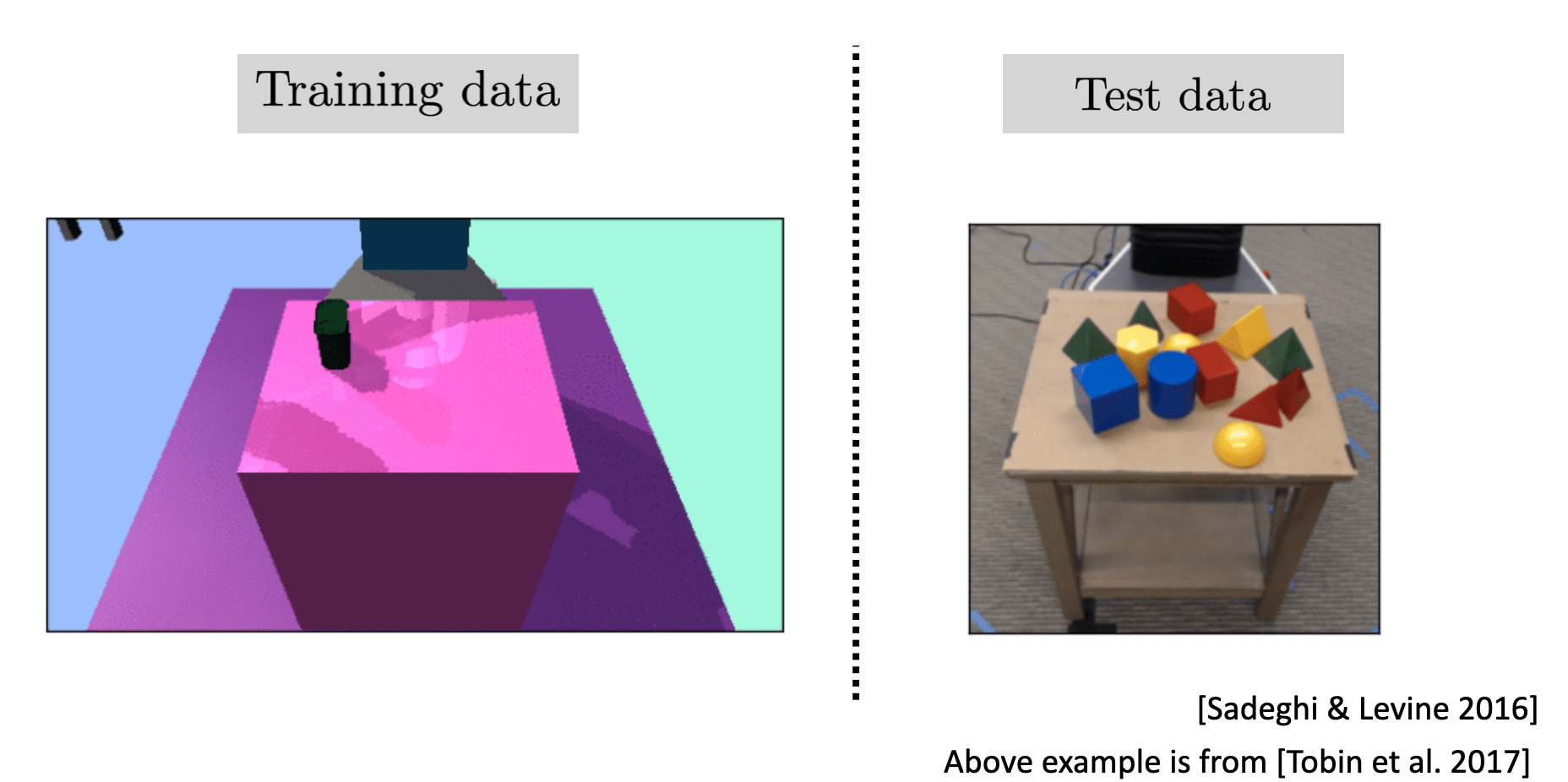
Case Study: Domain Shift in Autonomous Driving

Motivation

Let’s revisit domain shift — this time through the lens of a real-world application.
Autonomous driving gives us rich, practical examples of all types of shift.

Covariate Shift in Driving

Training: Urban, sunny, daytime data in California
Testing: Nighttime, fog, rain, snow — possibly in Europe

The input appearance changes drastically
But the meaning of features (e.g. pedestrians, signs) stays the same
This is a shift in P(X), while P(Y|X) stays stable

Visual Example: Covariate Shift

[Insert visual of sunny vs. foggy streets]

Same pedestrians, different pixel distributions

Label Shift in Driving

Training: Suburban setting — fewer pedestrians, many stop signs
Testing: City center near a school — more pedestrians and cyclists

Label frequencies change: P(Y) shifts
But each class still looks the same: P(X|Y) unchanged

Visual Example: Label Shift

[Insert bar plot of class distribution across domains]

Target domain has more bikes, fewer stop signs

Importance Weighting

To adapt label-shifted data:

Weight training samples by: w(y) = P_target(Y=y) / P_source(Y=y)
Helps rebalance what the model emphasizes during training

Q: how to adapt for co-variate shift?

Sim-to-real adaptation

Setting	Description
Unsupervised	No target labels
Semi-supervised	Few labeled target samples
Supervised	Fully labeled target data

Techniques include adversarial training, feature alignment, and fine-tuning

Wrap-Up: What Shift Did You See?

What kind of shift occurred?
How would you correct for it?
What’s the risk if we ignore the shift?

Domain shift is not rare — it’s constant in the real world.

Robustness

A Demo Lecture

Domain Shift:

Concepts, Techniques, and Applications