Lecture 4: Linear Classification
Intro to Machine Learning
\boxed{h}
Regression
Algorithm
\rightarrow
\(\mathcal{D}_\text{train}\)
\rightarrow
🧠⚙️
hypothesis class
loss function
hyperparameters
Recap:
regressor
\in \mathbb{R}^d
\in \mathbb{R}
y
\downarrow
"Use" a model
"Learn" a model
\rightarrow
\downarrow
x
\downarrow
Recap:
"Use" a model
"Learn" a model
\rightarrow
\downarrow
train, optimize, tune, adapt ...
adjusting/updating/finding \(\theta\)
gradient based
\boxed{h}
Regression
Algorithm
\rightarrow
\(\mathcal{D}_\text{train}\)
\rightarrow
🧠⚙️
hypothesis class
loss function
hyperparameters
regressor
\in \mathbb{R}^d
\in \mathbb{R}
y
\downarrow
\downarrow
x
predict, test, evaluate, infer ...
plug in the \(\theta\) found
no gradients involved
Classification
Algorithm
🧠⚙️
hypothesis class
loss function
hyperparameters
Today:
classifier
\in \mathbb{R}^d
\in \text{a discrete set}
\downarrow
x
y
\downarrow
\rightarrow
\boxed{h}
\(\mathcal{D}_\text{train}\)
\rightarrow
{"good", "better", "best", ...}
\(\{+1,0\}\)
\(\{😍, 🥺\}\)
{"Fish", "Grizzly", "Chameleon", ...}
Classification
Algorithm
🧠⚙️
hypothesis class
loss function
hyperparameters
classifier
\in
\downarrow
x
y
\downarrow
\rightarrow
\boxed{h}
\rightarrow
{"Fish", "Grizzly", "Chameleon", ...}
"Fish"
images adapted from Phillip Isola
features
label
\in \text{a discrete set}
Outline
- Linear (binary) classifiers
- to use: separator, normal vector
- to learn: difficult! won't do
- Linear logistic (binary) classifiers
- to use: sigmoid
- to learn: negative log-likelihood loss
- Linear multi-class classifiers
- to use: softmax
- to learn: one-hot encoding, cross-entropy loss
Outline
-
Linear (binary) classifiers
- to use: separator, normal vector
- to learn: difficult! won't do
- Linear logistic (binary) classifiers
- to use: sigmoid
- to learn: negative log-likelihood loss
- Linear multi-class classifiers
- to use: softmax
- to learn: one-hot encoding, cross-entropy loss
linear regressor
linear binary classifier
features
parameters
linear combination
predict
\(x \in \mathbb{R}^d\)
\(\theta \in \mathbb{R}^d, \theta_0 \in \mathbb{R}\)
\(\theta^T x +\theta_0\)
\(g = z\)
\(=z\)
if \(z > 0\)
otherwise
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
\(1\)
0
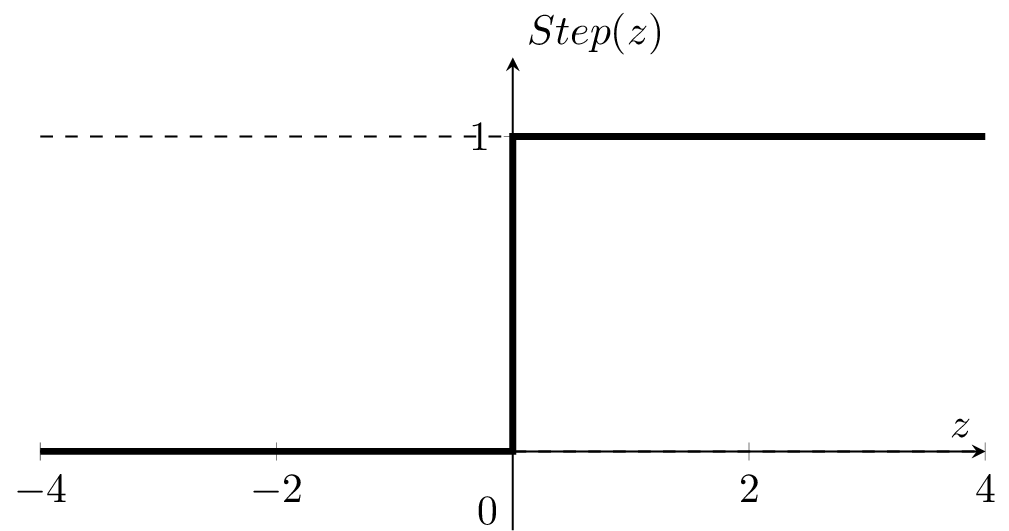
today, we refer to \(\theta^T x +\theta_0\) as \(z\) throughout.
\(g=\)
label
\(y\in \mathbb{R}\)
\(y\in \{0,1\}\)
Outline
-
Linear (binary) classifiers
- to use: separator, normal vector
- to learn: difficult! won't do
- Linear logistic (binary) classifiers
- to use: sigmoid
- to learn: negative log-likelihood loss
- Multi-class classifiers
- to use: softmax
- to learn: one-hot encoding, cross-entropy loss
\mathcal{L}_{01}(g, y)=\left\{\begin{array}{ll}
0 & \text { if } \text{guess} = \text{label} \\
1 & \text { otherwise }
\end{array}\right .
- To learn a model, need a loss function.
g = \operatorname{step}\left(z\right) = \operatorname{step}\left(\theta^{\top} x+\theta_0\right)
- Very intuitive, and easy to evaluate 😍
- One natural loss choice:
y
\mathcal{L}_{01}(g, a) = 0
\mathcal{L}_{01}(g, a) = 0
\mathcal{L}_{01}(g, a) = 0
\mathcal{L}_{01}(g, a) = 1
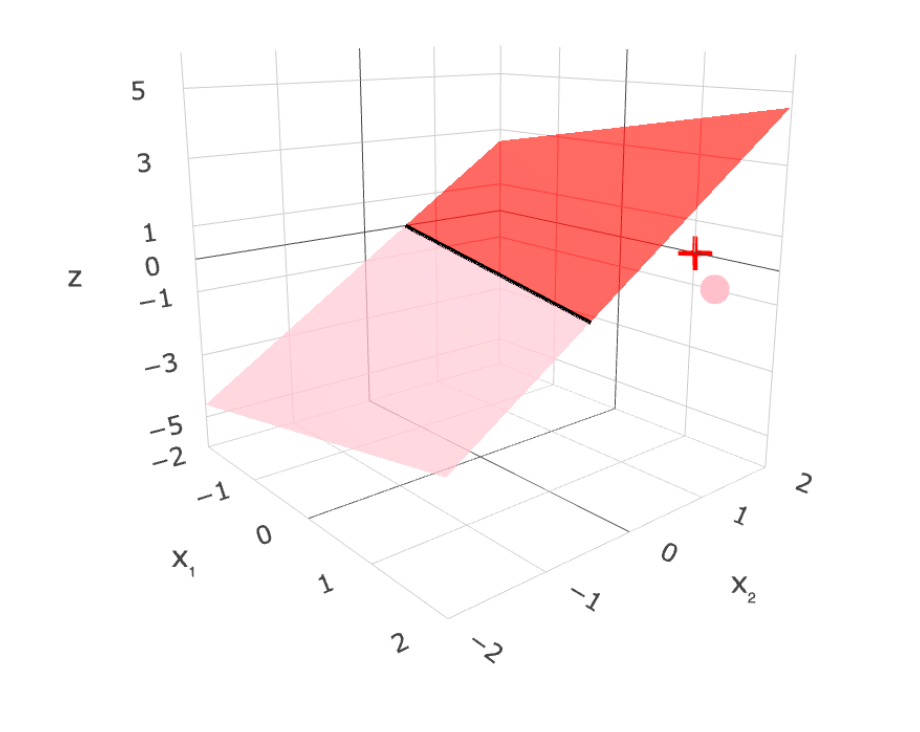
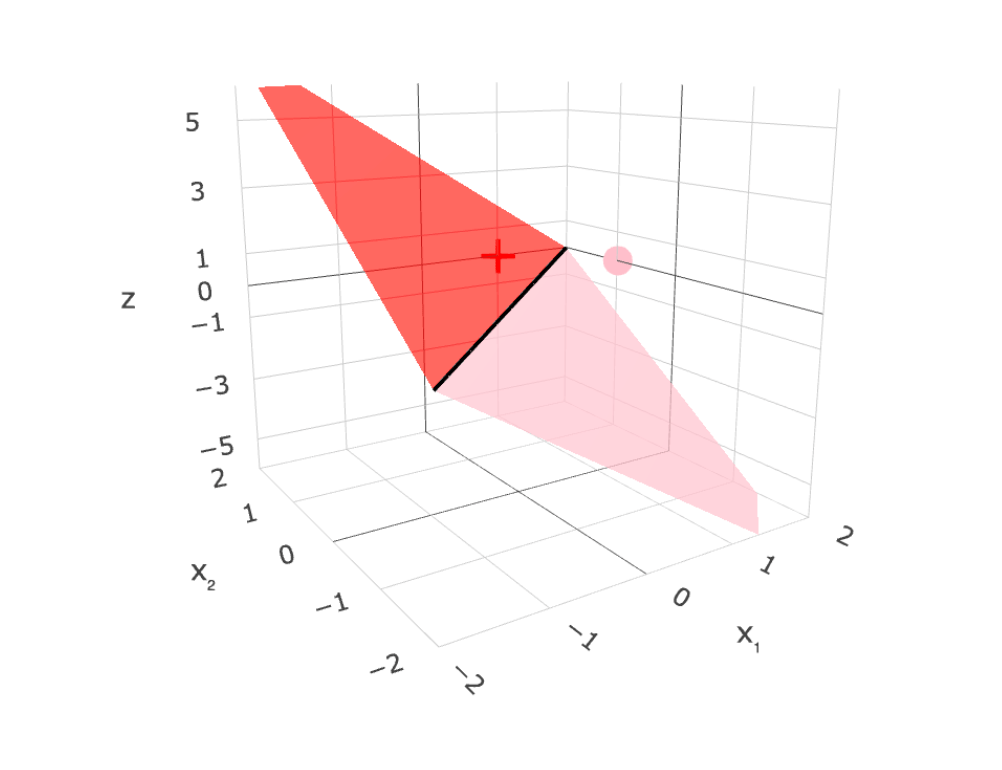
Very hard to optimize (NP-hard) 🥺
- "Flat" almost everywhere (zero gradient)
- "Jumps" elsewhere (no gradient)
linear binary classifier
features
parameters
linear combo
predict
\(x \in \mathbb{R}^d\)
\(\theta \in \mathbb{R}^d, \theta_0 \in \mathbb{R}\)
\(\theta^T x +\theta_0\)
\(=z\)
loss
\((g - y)^2 \)
\left\{\begin{array}{ll}
0 & \text { if } g = y \\
1 & \text { otherwise }
\end{array}\right .
g = z
linear regressor
closed-form or
gradient descent
NP-hard to learn
optimize via
if \(z > 0\)
otherwise
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
\(1\)
0
\(g=\)
\(y \in \mathbb{R}\)
\(y \in \{0,1\}\)
both discrete
Outline
- Linear (binary) classifiers
- to use: separator, normal vector
- to learn: difficult! won't do
-
Linear logistic (binary) classifiers
- to use: sigmoid
- to learn: negative log-likelihood loss
- Linear multi-class classifiers
- to use: softmax
- to learn: one-hot encoding, cross-entropy loss
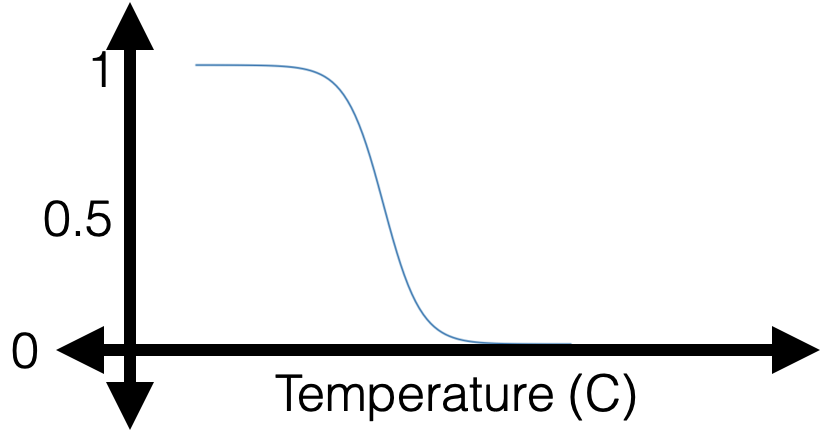
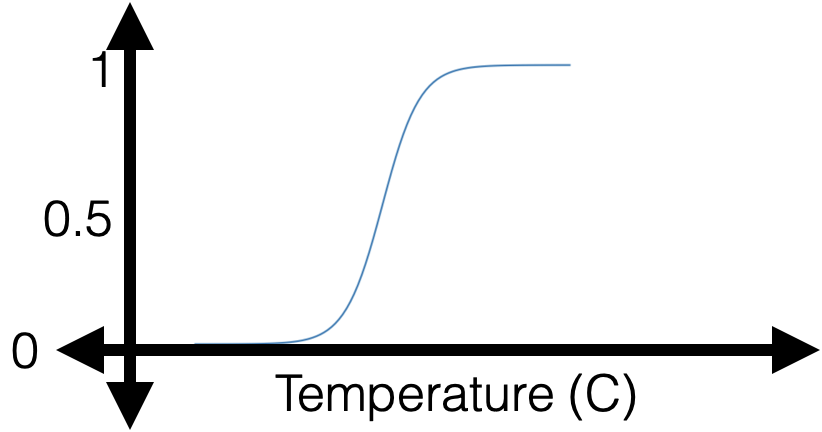
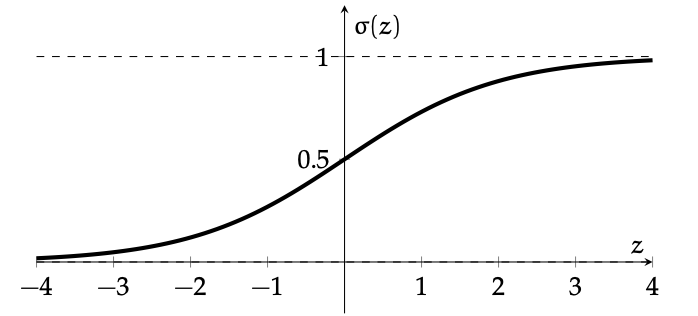
: a smooth step function
:= \frac{1}{1+e^{-z}}
Sigmoid
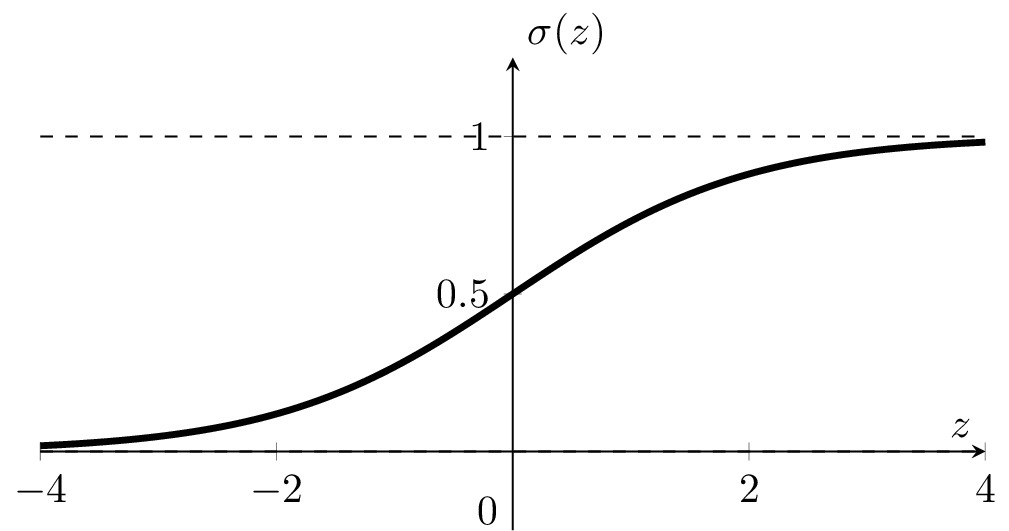
if \(z > 0\)
otherwise
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
\(1\)
0
if \(\sigma(z) > 0.5\)
otherwise
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
\(1\)
0
Predict
Predict
\(z\) is called the logit
linear binary classifier
features
parameters
linear combo
predict
\(x \in \mathbb{R}^d\)
\(\theta \in \mathbb{R}^d, \theta_0 \in \mathbb{R}\)
\(\theta^T x +\theta_0\)
\(=z\)
linear logistic binary classifier
if \(z > 0\)
otherwise
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
\(1\)
0
if \(\sigma(z) > 0.5\)
otherwise
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
\(1\)
0
:= \frac{1}{1+e^{-z}}
features
parameters
linear combo
predict
\(x \in \mathbb{R}^d\)
\(\theta \in \mathbb{R}^d, \theta_0 \in \mathbb{R}\)
\(\theta^T x +\theta_0\)
\(=z\)
linear logistic binary classifier
if \(\sigma(z) > 0.5\)
otherwise
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
\(1\)
0
-
Sigmoid squashes the logit \(z\) into a number in \((0, 1)\).
= \frac{1}{1+e^{-\left(\theta^{\top} x+\theta_0\right)}}
if \(\sigma(z) \)
> 0.5
-
Predict positive class label 1
= \frac{1}{1+e^{-z}}
-
The logit \(z\) is a linear combo of \(x\) via the parametes.
\(\sigma\left(\cdot\right):\) the model's confidence or estimated likelihood that feature \(x\) belongs to the positive class.
- \(\theta\), \(\theta_0\) can flip, squeeze, expand, or shift the \(\sigma\left(x\right)\) graph horizontally
- \(\sigma\left(\cdot\right)\) monotonic, very elegant gradient (see hw/lab)
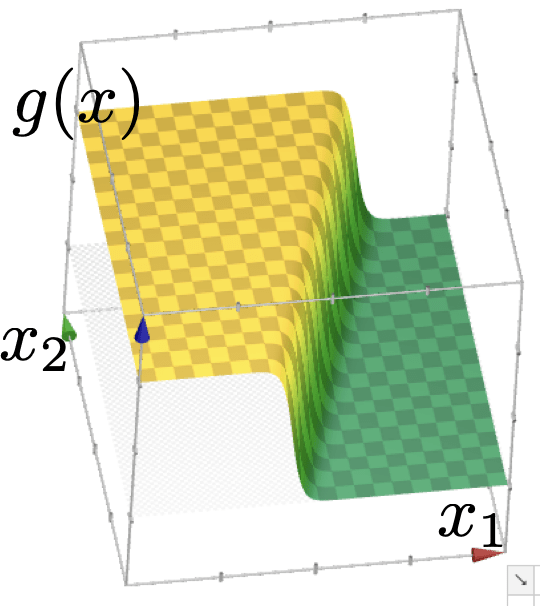
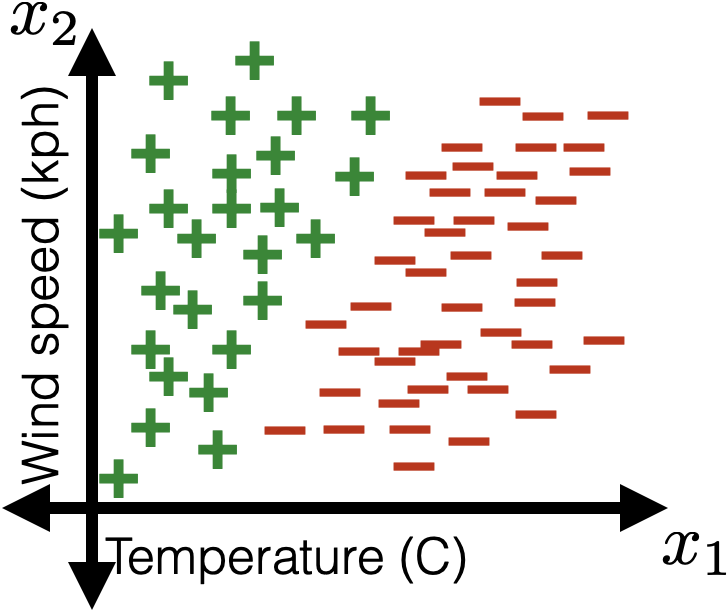
images credit: Tamara Broderick
linear separator
\(z = \theta^T x+\theta_0=0\)
1d feature
2d feature
features
parameters
linear combo
predict
\(x \in \mathbb{R}^d\)
\(\theta \in \mathbb{R}^d, \theta_0 \in \mathbb{R}\)
\(\theta^T x +\theta_0\)
\(=z\)
linear logistic binary classifier
if \(\sigma(z) > 0.5\)
otherwise
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
\(1\)
0
\quad \quad
\sigma
\sigma(x)
Outline
- Linear (binary) classifiers
- to use: separator, normal vector
- to learn: difficult! won't do
- Linear logistic (binary) classifiers
- to use: sigmoid
- to learn: negative log-likelihood loss
- Linear multi-class classifiers
- to use: softmax
- to learn: one-hot encoding, cross-entropy loss
\mathcal{L}_{01}(g, y)=\left\{\begin{array}{ll}
0 & \text { if } g = y \\
1 & \text { otherwise }
\end{array}\right .
\mathcal{L}_{\text{nll}}(g, y)
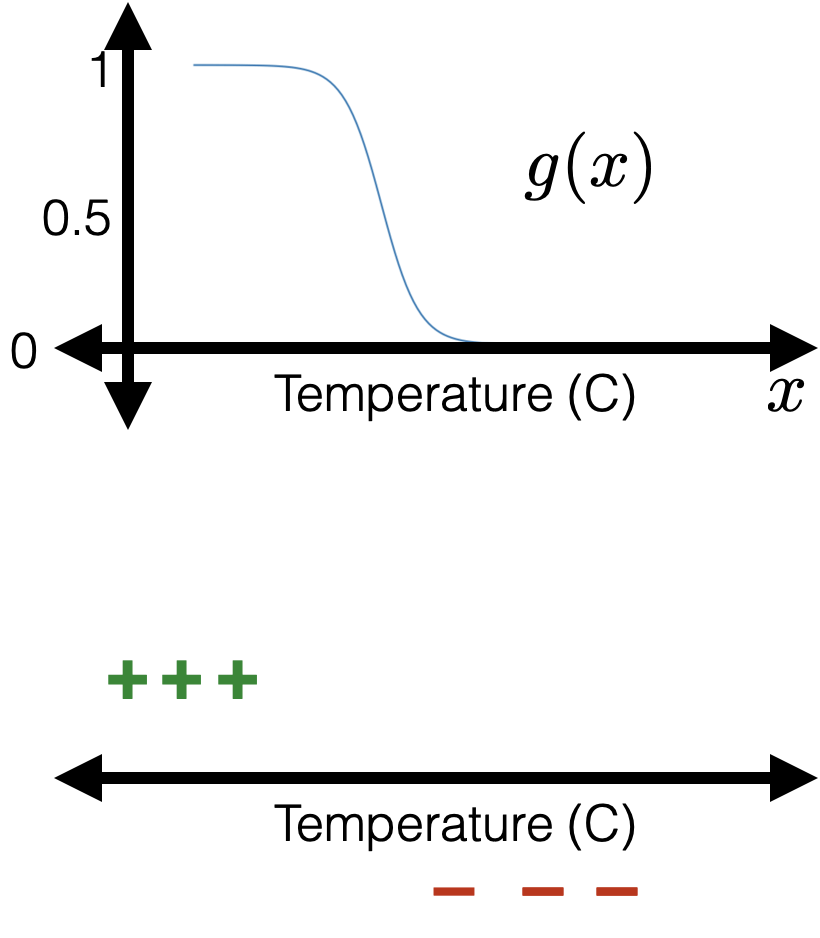
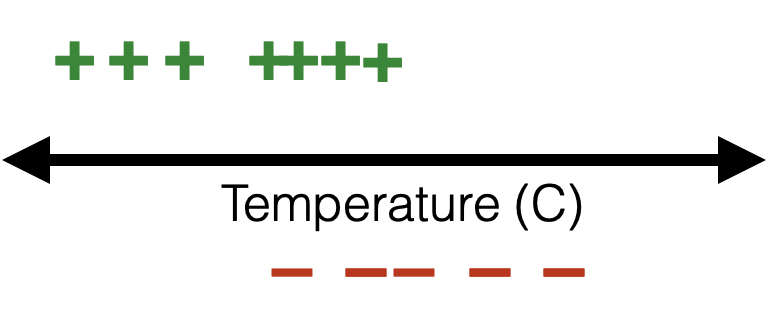
- if true label \(y=1,\) we'd like guess \(g\) to just be \(1\)... difficult ask
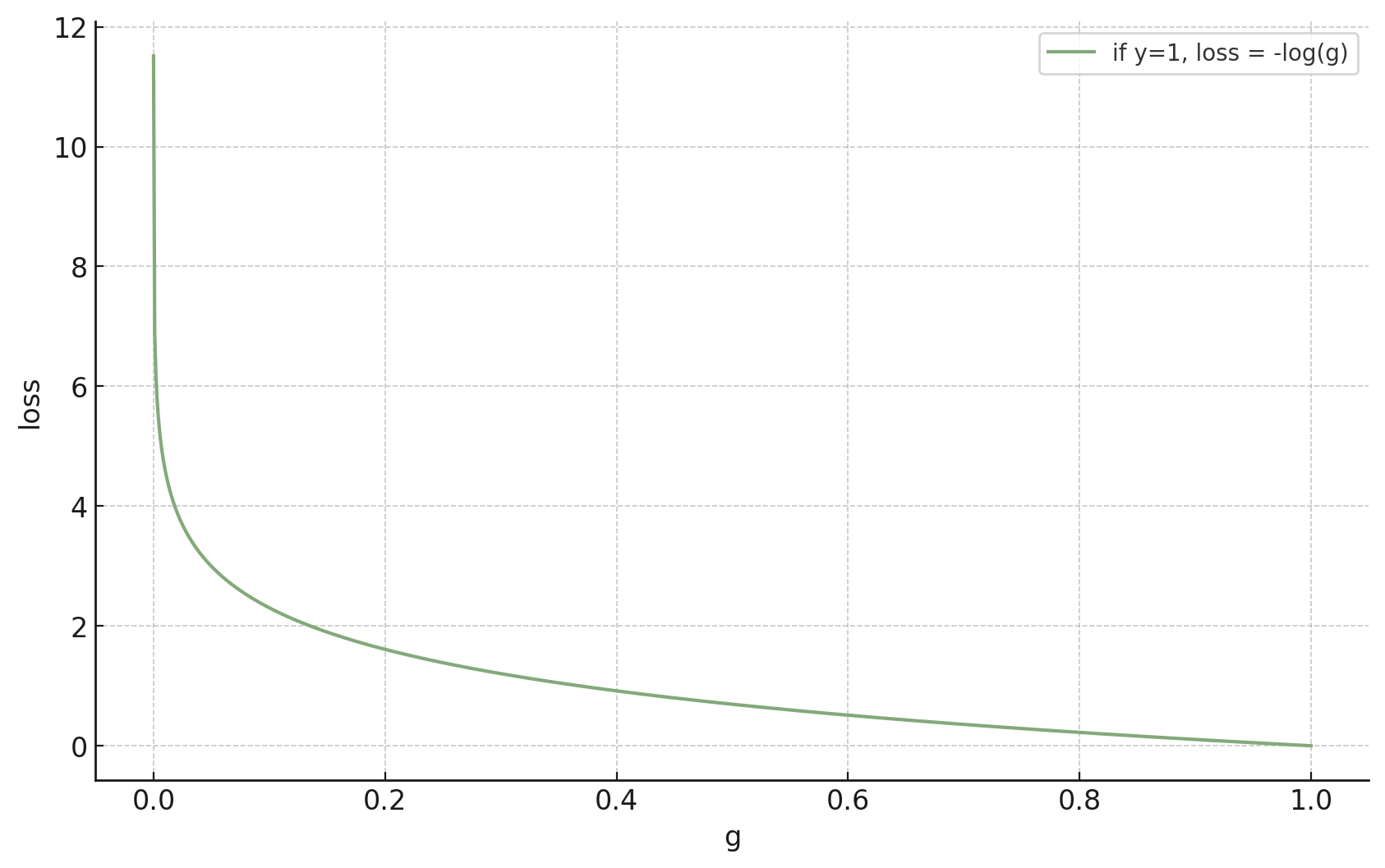
now:
- if true label \(y=1,\) we'd like the guess \(g\) to gradually approach \(1\)
👇
previously:
:=-\log(g)
= \mathcal{L}_{\text{nll}}(g, 1)
negative
log
likelihood
\(g=\sigma\left(\cdot\right):\) the model's confidence or estimated likelihood that feature \(x\) belongs to the positive class.
training data:
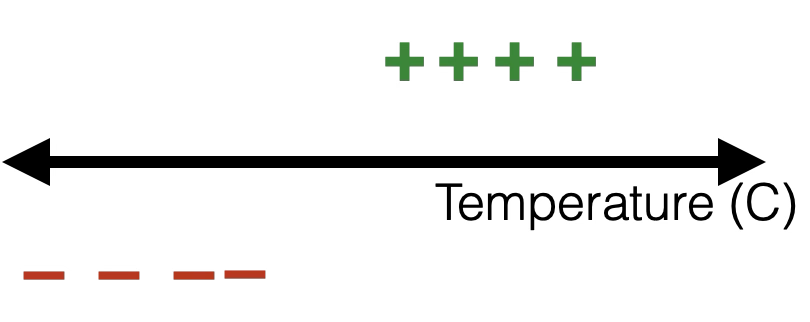
true label \(y\) is \(1\)
👇
\mathcal{L}_{\text{nll}}(g, y)
:=-\log(g)
= \mathcal{L}_{\text{nll}}(g, 1)
\mathcal{L}_{\text{nll}}(g, y)
- if true label \(y=0,\) we'd like the guess \(g\) to gradually approach \(0\)
👇
:=-\log(1-g)
= \mathcal{L}_{\text{nll}}(g, 0)
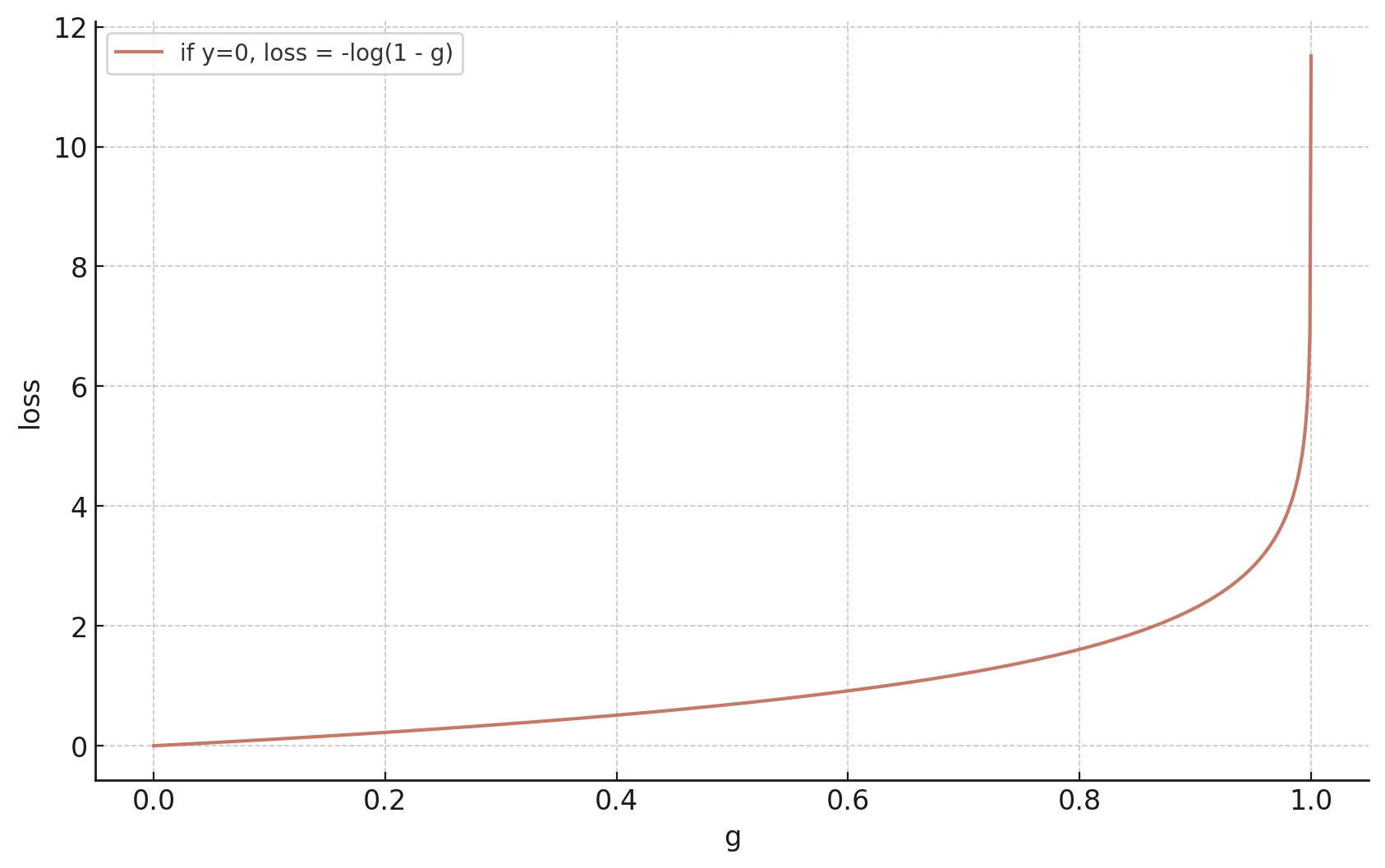
\(g = \sigma\left(\cdot\right):\) the model's confidence or estimated likelihood that feature \(x\) belongs to the positive class.
\(1-g = 1-\sigma\left(\cdot\right):\) the model's confidence or estimated likelihood that feature \(x\) belongs to the negative class.
training data:
\mathcal{L}_{\text{nll}}(g, y)= \mathcal{L}_{\text{nll}}(g, 0)=-\log(1-g)
true label \(y\) is \(0\)
👇
Combining both cases, since the actual label \(y \in \{+1,0\}\)
= - \left[y \log g +\left(1-y \right) \log \left(1-g\right)\right]
\mathcal{L}_{\text {nll }}(g,y)
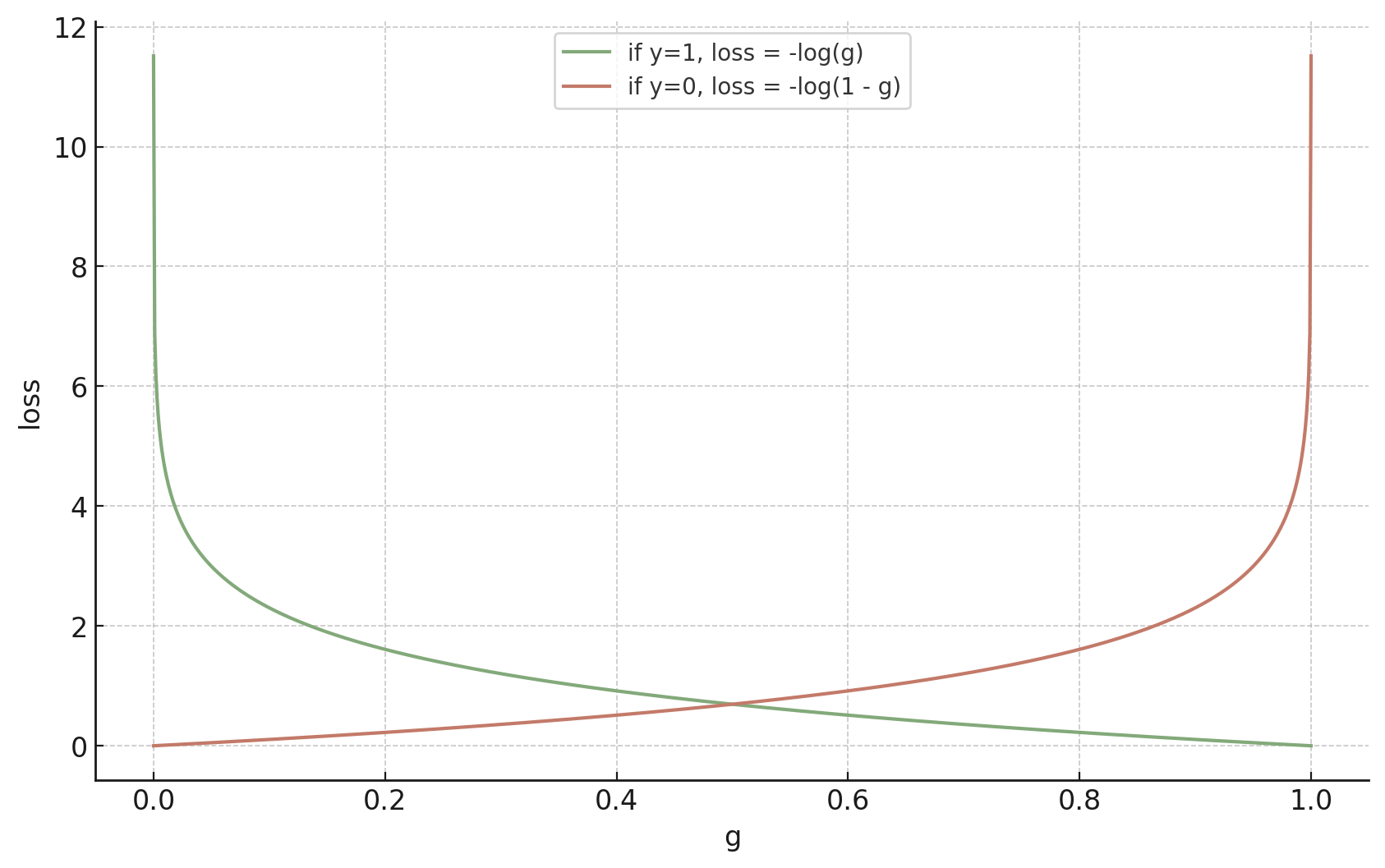
training data:
😍
🥺
= - \left[y \log g +\left(1-y \right) \log \left(1-g \right)\right]
\mathcal{L}_{\text {nll }}({ g, y })
When \(y = 1\)
😍
🥺
g(x)=\sigma\left(\theta x+\theta_0\right)
g
g
= - \log g
training data:
😍
🥺
When \(y = 0\)
😍
🥺
g(x)=\sigma\left(\theta x+\theta_0\right)
g
g
= - \left[y \log g +\left(1-y \right) \log \left(1-g \right)\right]
= - \left[\log \left(1-g \right)\right]
\mathcal{L}_{\text {nll }}({ g, y })
training data:
true label \(y\) is \(1\)
👇
\mathcal{L}_{\text{nll}}(g, y)
:=-\log(g)
= \mathcal{L}_{\text{nll}}(g, 1)
linear
binary classifier
features
parameters
linear combo
predict
\(x \in \mathbb{R}^d\)
\(\theta \in \mathbb{R}^d, \theta_0 \in \mathbb{R}\)
\(\theta^T x +\theta_0\)
\(=z\)
linear logistic
binary classifier
loss
\((g - y)^2 \)
- \left[y \log g +\left(1-y \right) \log \left(1-g\right)\right]
\left\{\begin{array}{ll}
0 & \text { if } g = y \\
1 & \text { otherwise }
\end{array}\right .
\left\{\begin{array}{ll}
1 & \text { if } z>0 \\
0 & \text { otherwise }
\end{array}\right .
\left\{\begin{array}{ll}
1 & \text { if } g = \sigma(z)>0.5 \\
0 & \text { otherwise }
\end{array}\right .
g = z
linear regressor
closed-form or
gradient descent
NP-hard to learn
- gradient descent
- regularization still important
optimize via
label
\(y \in \mathbb{R}\)
\(y \in \{0,1\}\)
Outline
- Linear (binary) classifiers
- to use: separator, normal vector
- to learn: difficult! won't do
- Linear logistic (binary) classifiers
- to use: sigmoid
- to learn: negative log-likelihood loss
-
Multi-class classifiers
- to use: softmax
- to learn: one-hot encoding, cross-entropy loss
Video edited from: HBO, Sillicon Valley
features
parameters
linear combo
predict
\(x \in \mathbb{R}^d\)
\(\theta \in \mathbb{R}^d, \theta_0 \in \mathbb{R}\)
\(\theta^T x +\theta_0\)
\(=z\)
linear logistic binary classifier
if \(\sigma(z) > 0.5\)
otherwise
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
\(1\)
0
🌭
\(x\)
\(z \in \mathbb{R}\)
scalar logit
\sigma(z) \in \mathbb{R}
- \(\sigma\left(\cdot\right):\) the model's confidence or estimated likelihood that feature \(x\) belongs to the hotdog class;
- \(1-\sigma\left(\cdot\right):\) the not-hotdog class.
scalar likelihood
(raw hotdog-ness)
(normalized probability of hotdog-ness)
to predict among \(K\) categories
say \(K=3\) categories: \(\{\)hot-dog, pizza, salad\(\}\)
\(K\) logits
\text{softmax}(z)\in \mathbb{R}^3
\(K\)-class likelihood
raw likelihood of each category
distribution over the categories
\(z \in \mathbb{R}^3\)
to predict hotdog or not,
a scalar logit suffices
🌭
\(x\)
🌭
\(x\)
\(z \in \mathbb{R}\)
\sigma(z) \in \mathbb{R}
\(K\) classes
two classes
\(\theta \in \mathbb{R}^d, \theta_0 \in \mathbb{R}\)
\(\theta \in \mathbb{R}^{d \times K},\)
\(\theta_0 \in \mathbb{R}^{K}\)
\text{softmax}(z)\in \mathbb{R}^K
\(z \in \mathbb{R}^K\)
🌭
\(x\)
🌭
\(x\)
\(z \in \mathbb{R}\)
\sigma(z) \in \mathbb{R}
raw likelihood of each category
\(K\) classes
two classes
🌭
\(x\)
🌭
\(x\)
\(z \in \mathbb{R}\)
\(z \in \mathbb{R}^K\)
\sigma(z) \in \mathbb{R}
\text{softmax}(z)\in \mathbb{R}^K
raw likelihood of each category
distribution over \(K\) categories
\dots
\left\}
\begin{array}{l}
\\
\\
\\
\end{array}
\right.
\begin{bmatrix}
1 \\
2 \\
3
\end{bmatrix}
=\begin{bmatrix}
\frac{e^{1}}{e^{1} + e^{2} + e^{3}} \\[6pt]
\frac{e^{2}}{e^{1} + e^{2} + e^{3}} \\[6pt]
\frac{e^{3}}{e^{1} + e^{2} + e^{3}}
\end{bmatrix}
=\begin{bmatrix}
0.0900 \\[6pt]
0.2447 \\[6pt]
0.6653
\end{bmatrix}
\operatorname{softmax}
\left(
\begin{array}{l}
\\
\\
\\
\end{array}
\right.
\left)
\begin{array}{l}
\\
\\
\\
\end{array}
\right.
each output entry is between 0 and 1, and their sum is 1
max in the input
"soft" max'd in the output
\operatorname{softmax}(z) :=
\begin{bmatrix}
\frac{\exp(z_1)}{\sum_{k=1}^K \exp(z_k)} \\[6pt]
\vdots \\[6pt]
\frac{\exp(z_K)}{\sum_{k=1}^K \exp(z_k)}
\end{bmatrix}
softmax:
\mathbb{R}^K \to \mathbb{R}^K
e.g.
sigmoid
= \frac{\exp(z)}{\exp(z) +\exp (0)}
\sigma(z):=\frac{1}{1+\exp (-z)}
\mathbb{R} \to \mathbb{R}
predict the category with the highest softmax score
\operatorname{softmax}(z) :=
\begin{bmatrix}
\frac{\exp(z_1)}{\sum_{k=1}^K \exp(z_k)} \\[6pt]
\vdots \\[6pt]
\frac{\exp(z_K)}{\sum_{k=1}^K \exp(z_k)}
\end{bmatrix}
softmax:
\mathbb{R}^K \to \mathbb{R}^K
predict positive if \(\sigma(z)>0.5 = \sigma(0)\)
equivalently, predicting the category with the largest raw logit.
implicit logit for the negative class
features
parameters
linear combo
predict
\(x \in \mathbb{R}^d\)
\(\theta \in \mathbb{R}^d, \theta_0 \in \mathbb{R}\)
\(\theta^T x +\theta_0\)
\(=z \in \mathbb{R}\)
linear logistic
binary classifier
one-out-of-\(K\) classifier
\(\theta \in \mathbb{R}^{d \times K},\)
\(=z \in \mathbb{R}^{K}\)
\(\theta^T x +\theta_0\)
predict positive if \(\sigma(z)>\sigma(0)\)
predict the category with the highest softmax score
\operatorname{softmax}(z) =
\begin{bmatrix}
\frac{\exp(z_1)}{\sum_{k=1}^K \exp(z_k)} \\[6pt]
\vdots \\[6pt]
\frac{\exp(z_K)}{\sum_{k=1}^K \exp(z_k)}
\end{bmatrix}
\sigma(z) = \frac{\exp(z)}{\exp(0) +\exp (z)}
\(\theta_0 \in \mathbb{R}^{K}\)
Outline
- Linear (binary) classifiers
- to use: separator, normal vector
- to learn: difficult! won't do
- Linear logistic (binary) classifiers
- to use: sigmoid
- to learn: negative log-likelihood loss
-
Multi-class classifiers
- to use: softmax
- to learn: one-hot encoding, cross-entropy loss
image adapted from Phillip Isola
K =3
One-hot encoding:
- Generalizes from {0,1} binary labels
- Encode the \(K\) classes as an \(\mathbb{R}^K\) vector, with a single 1 (hot) and 0s elsewhere.
column vectors
flipped due to slides real-estate
\mathcal{L}_{\mathrm{nllm}}({g}, y)=-\sum_{{k}=1}^{{K}}y_{{k}} \cdot \log \left({g}_{{k}}\right)
- Generalizes negative log likelihood loss \(\mathcal{L}_{\mathrm{nll}}({g}, {y})= - \left[y \log g +\left(1-y \right) \log \left(1-g \right)\right]\)
-
Although this is written as a sum over \(K\) terms, for a given training data point, only the term corresponding to its true class label contributes, since all other \(y_k=0\)
Negative log-likelihood \(K-\) classes loss (aka, cross-entropy)
\(y:\)one-hot encoding label
\(y_{{k}}:\) \(k\)th entry in \(y\), either 0 or 1
\(g:\) softmax output
\(g_{{k}}:\) probability or confidence of belonging in class \(k\)
current prediction
\(g=\text{softmax}(\cdot)\)
feature \(x\)
true label \(y\)
\log(g)
y
[0,0,0,0,0,1,0,0, \ldots]
image adapted from Phillip Isola
loss \(\mathcal{L}_{\mathrm{nllm}}({g}, y)\\=-\sum_{{k}=1}^{{K}}y_{{k}} \cdot \log \left({g}_{\mathrm{k}}\right)\)
feature \(x\)
true label \(y\)
\log(g)
y
[0,0,1,0,0,0,0,0, \ldots]
current prediction
\(g=\text{softmax}(\cdot)\)
image adapted from Phillip Isola
loss \(\mathcal{L}_{\mathrm{nllm}}({g}, y)\\=-\sum_{{k}=1}^{{K}}y_{{k}} \cdot \log \left({g}_{\mathrm{k}}\right)\)
Classification
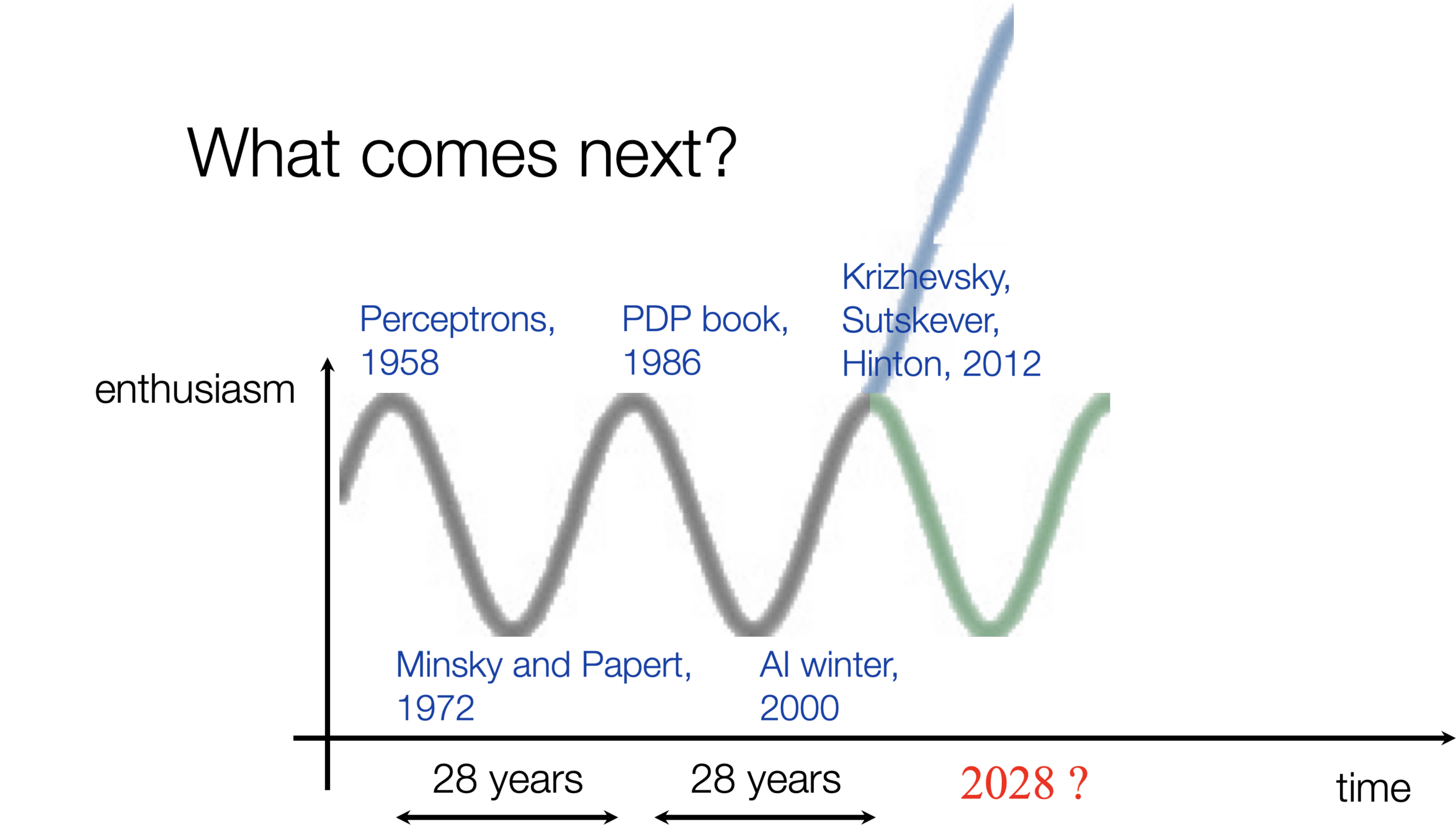
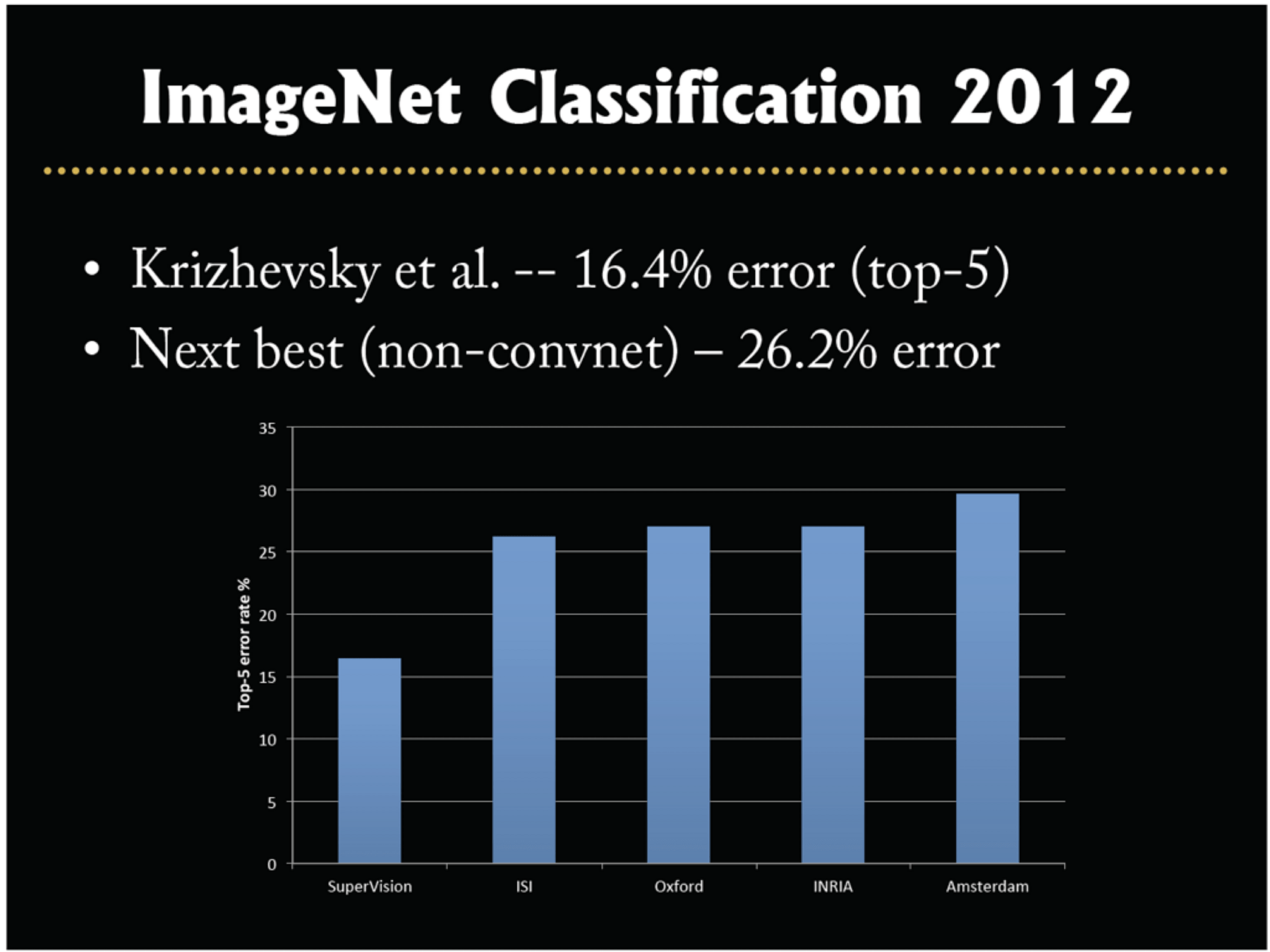
Image classification played a pivotal role in kicking off the current wave of AI enthusiasm.
Summary
- Classification: a supervised learning problem, similar to regression, but where the output/label is in a discrete set.
- Binary classification: only two possible label values.
- Linear binary classification: think of \(\theta\) and \(\theta_0\) as defining a hyperplane that cuts the d-dimensional feature space into two half-spaces.
- 0-1 loss: a natural loss function for classification, BUT, hard to optimize.
- Sigmoid function: smoother and probabilistic step function, motivation and properties.
- NLL loss: smooth loss and has nice probabilistic motivations. Can optimize via (S)GD.
- Regularization is still important.
- The generalization to multi-class via (one-hot encoding, and softmax mechanism)
- Other ways to generalize to multi-class (see hw/lab)
Thanks!
We'd love to hear your thoughts.
\rightarrow
\rightarrow
new feature
"Fish"
new prediction
{"Fish", "Grizzly", "Chameleon", ...}
\boxed{h}
\downarrow
x
y \in
\downarrow
Regression
Algorithm
🧠⚙️
hypothesis class
loss function
hyperparameters
images adapted from Phillip Isola
features
label
🌭
\(x\)
\(\theta^T x +\theta_0\)
\(z \in \mathbb{R}\)
if we want to predict among \(K\) categories
say \(K=4\) categories: \(\{\)hot-dog, pizza, pasta, salad\(\}\)
❓
\(z \in \mathbb{R}^4\)
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
distribution over these 4 categories
4 logits, each one a raw summary of the corresponding food category
🌭
\(x\)
\(\theta^T x +\theta_0\)
\(z \in \mathbb{R}^3\)
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
distribution over these 3 categories
❓
if we want to predict among \(K\) categories
say \(K=3\) categories: \(\{\)hot-dog, pizza, salad\(\}\)
Outline
- Linear (binary) classifiers
- to use: separator, normal vector
- to learn: difficult! won't do
- Linear logistic (binary) classifiers
- to use: sigmoid
- to learn: negative log-likelihood loss
-
Multi-class classifiers
- to use: softmax
- to learn: one-hot encoding, cross-entropy loss
Linear Logistic Classifier
- Mainly motivated to address the gradient issue in learning a "vanilla" linear classifier
-
The gradient issue is caused by both the 0/1 loss, and the sign functions nested in.
-
\mathcal{L}_{01}(x^{(i)}, y^{(i)}; \theta, \theta_0)=\left\{\begin{array}{ll}
0 & \text { if } \operatorname{sign}\left(\theta^{\top} x^{(i)}+\theta_0\right) = y^{(i)} \\
1 & \text { otherwise }
\end{array}\right .
- But has nice probabilistic interpretation too.
-
As before, let's first look at how to make prediction with a given linear logistic classifier
(Binary) Linear Logistic Classifier
- Each data point:
- features \([x_1, x_2, \dots x_d]\)
- label \(y \in\){positive, negative}
- A (binary) linear logistic classifier is parameterized by \([\theta_1, \theta_2, \dots, \theta_d, \theta_0]\)
- To use a given classifier make prediction:
- do linear combination: \(z =({\theta_1}x_1 + \theta_2x_2 + \dots + \theta_dx_d) + \theta_0\)
- predict positive label if
otherwise, negative label.
\sigma(z) = \sigma\left(\theta^{\top} x+\theta_0\right)
= \frac{1}{1+e^{-z}}
= \frac{1}{1+e^{-\left(\theta^{\top} x+\theta_0\right)}}
> 0.5
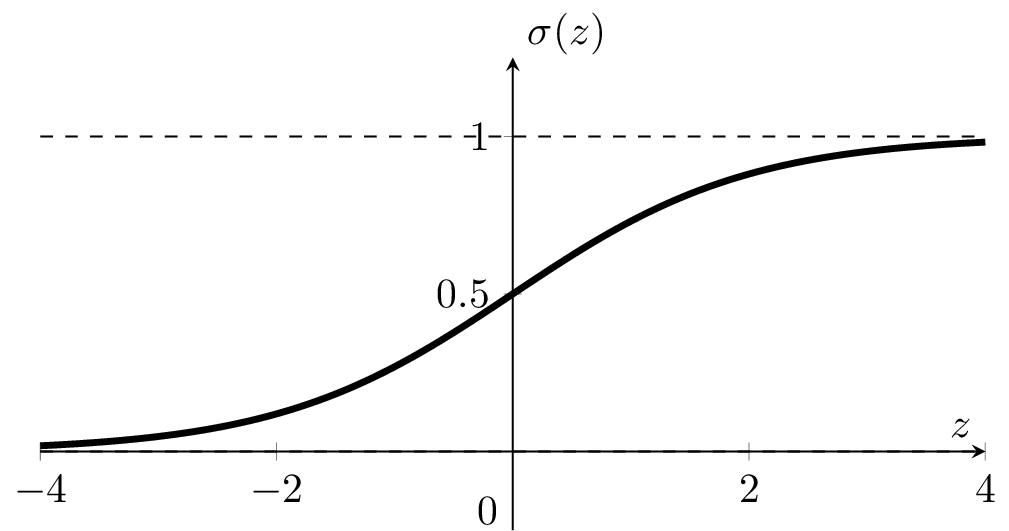
: a smooth step function
= \frac{1}{1+e^{-z}}
Sigmoid
if \(\sigma(z) > 0.5\)
otherwise
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
\(1\)
0
🌭
\(x\)
\(\theta^T x +\theta_0\)
\(z \in \mathbb{R}\)
\(\sigma(z) :\) model's confidence the input \(x\) is a hot-dog
learned scalar "summary" of "hot-dog-ness"
\(1-\sigma(z) :\) model's confidence the input \(x\) is not a hot-dog
fixed baseline of "non-hot-dog-ness"
training data:
😍
🥺
Recall, the labels \(y \in \{+1,0\}\)
g(x)=\sigma\left(\theta x+\theta_0\right)
= -[\text { actual } \cdot \log (\text { guess })+(1-\text { actual }) \cdot \log (1-\text { guess })]
= - \left[y \log g +\left(1-y \right) \log \left(1-g\right)\right]
\mathcal{L}_{\text {nll }}(\text { guess, actual })
g
g
training data:
😍
🥺
= - \left[y \log g +\left(1-y \right) \log \left(1-g \right)\right]
\mathcal{L}_{\text {nll }}(\text { guess, actual })
If \(y = 1\)
😍
🥺
g(x)=\sigma\left(\theta x+\theta_0\right)
g
g
= - \log g
training data:
😍
🥺
If \(y = 0\)
😍
🥺
g(x)=\sigma\left(\theta x+\theta_0\right)
g
g
= - \left[y \log g +\left(1-y \right) \log \left(1-g \right)\right]
\mathcal{L}_{\text {nll }}(\text { guess, actual })
= - \left[\log \left(1-g \right)\right]
training data:
= - \left[y \log g +\left(1-y \right) \log \left(1-g \right)\right]
\mathcal{L}_{\text {nll }}(\text { guess, actual })
= - \log g
linear
binary classifier
features
parameters
linear
combination
predict
\(x \in \mathbb{R}^d\)
\(A \in \mathbb{R}^{n \times n}, \theta_0 \in \mathbb{R}\)
\(\theta^T x +\theta_0\)
\(=z\)
linear logistic
binary classifier
if \(z > 0\)
otherwise
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
\(1\)
0
if \(\sigma(z) > 0.5\)
otherwise
\left\{
\begin{array}{l}
\\
\\
\end{array}
\right.
\(1\)
0
\(X \in \mathbb{R}^{n \times d}\)
6.390 IntroML (Fall25) - Lecture 4 Linear Classification
By Shen Shen
