
Lecture 2: Generative Models - Autoregressive
Shen Shen
April 2, 2025
2:30pm, Room 32-144
Slides adapted from Kaiming He
Modeling with Machine Learning for Computer Science


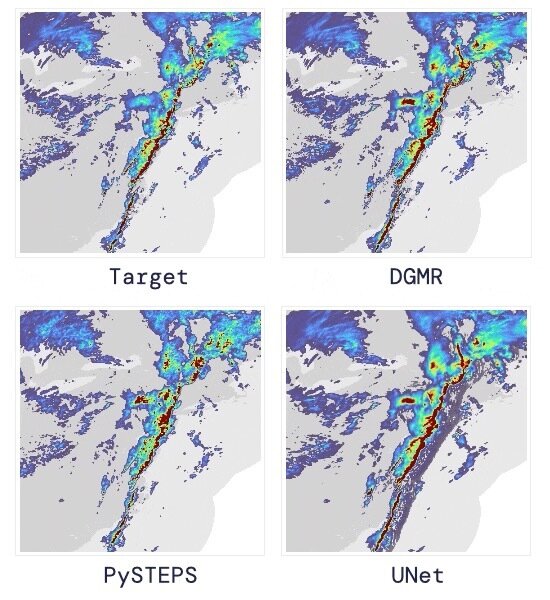
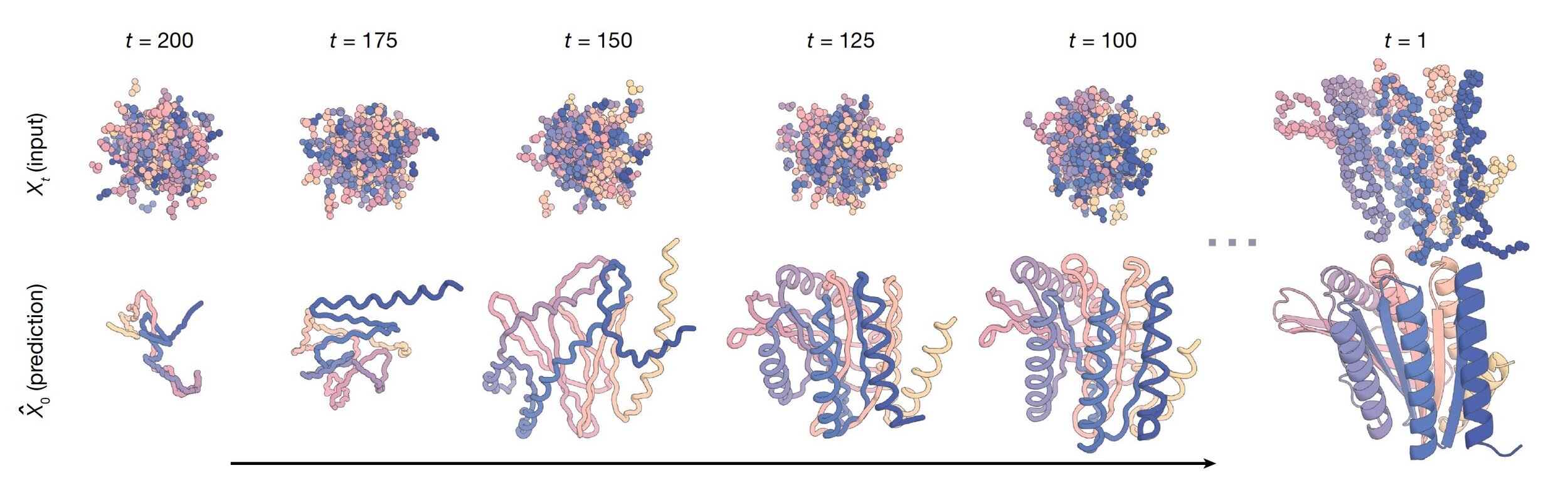
Discriminative v.s. Generative Models
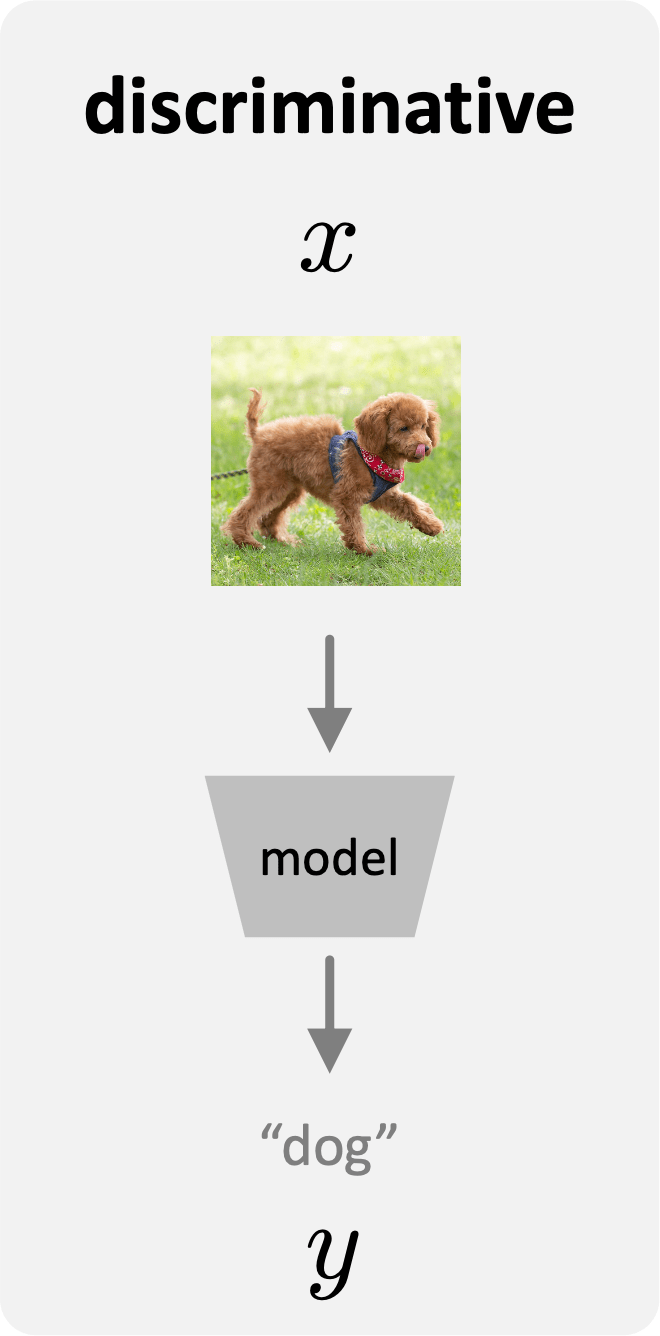
discriminative:
- "feature/sample" \(x\) to "label" \(y\)
- one "desired" output
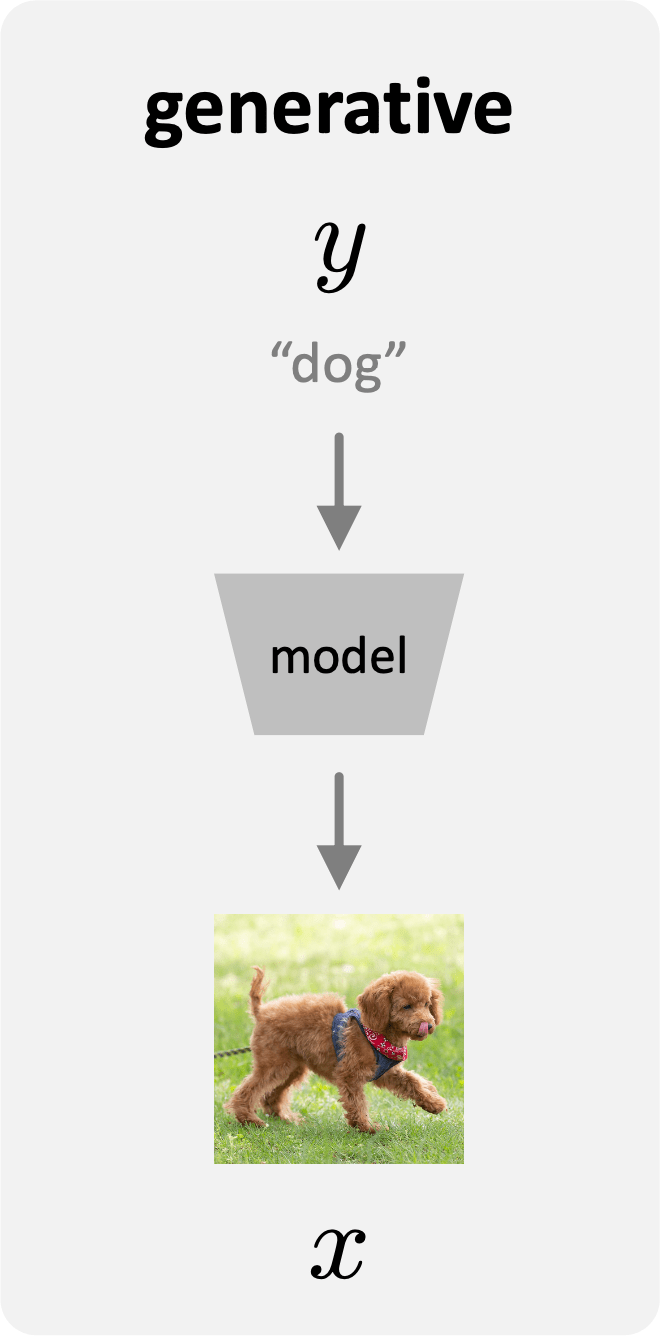
generative:
- "label" \(y\) to "feature/sample" \(x\)
- many possible outputs
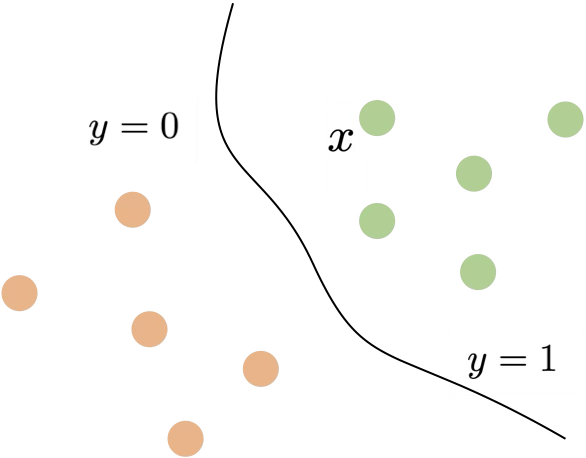
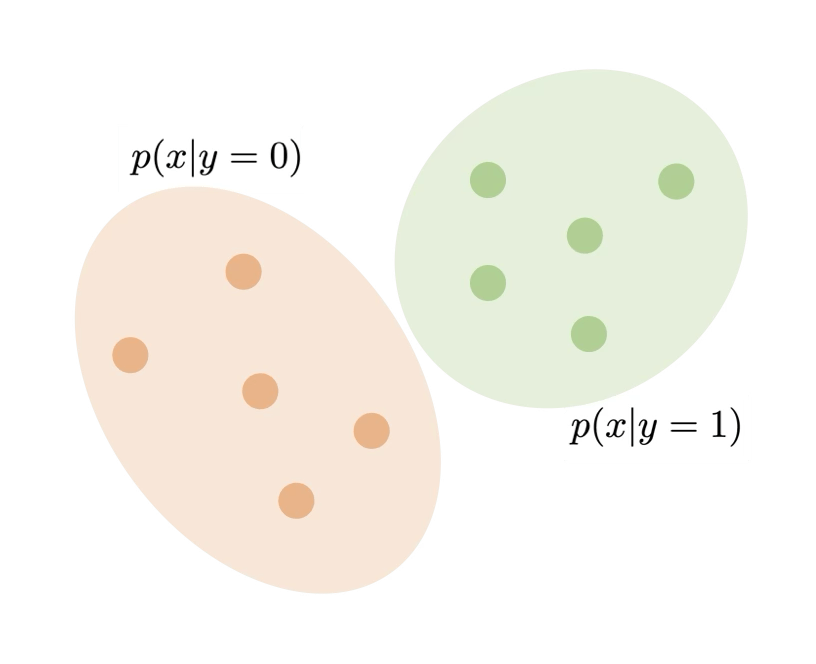
Discriminative v.s. Generative Models
discriminative: \(p(y \mid x)\)
generative: \(p(x \mid y)\)
Generative models are about \(p(x \mid y)\)
What can be \(y\)?
- condition
- constraint
- labels
- attributes
...
What can be \(x\)?
- “data”
- samples
- observations
- measurements
...
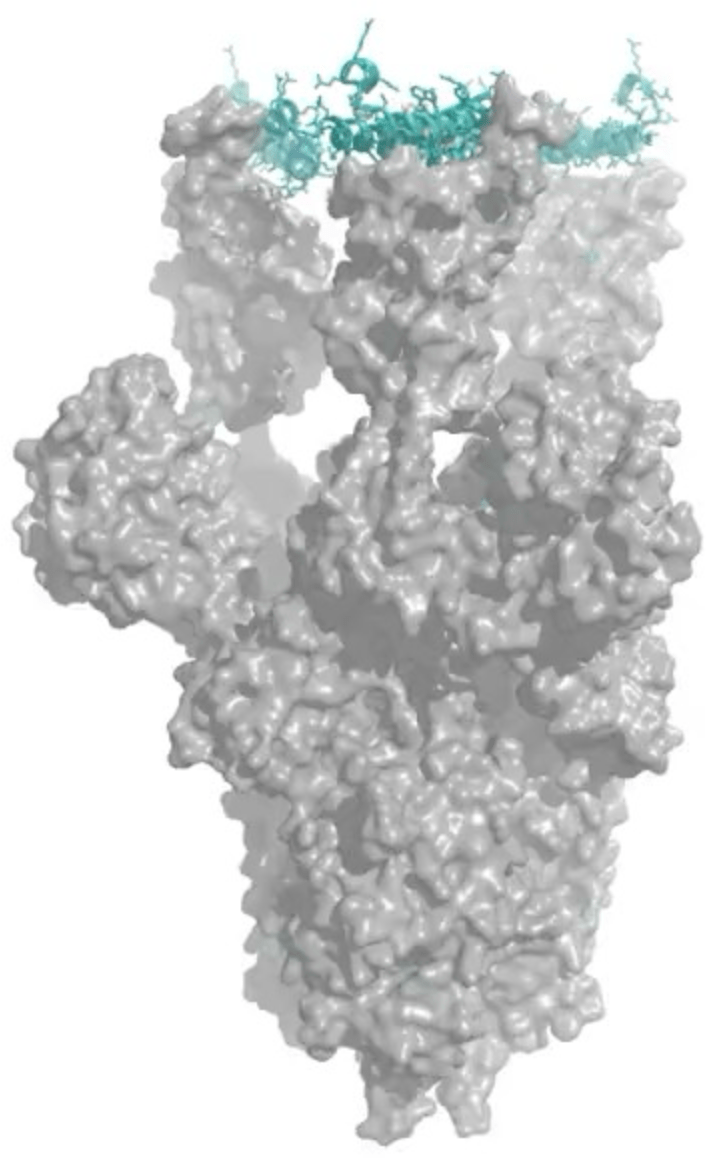
Model the task as \(p(x \mid y)\)
\(y\) : condition/constraint (e.g., symmetry)
\(x\) : generated protein structures
Protein structure generation
Model the task as \(p(x \mid y)\)
\(y\) :
text prompt
\(x\) :
response of a chatbot
Text-to-image/video generation
Prompt: teddy bear teaching a course, with
"generative models" written on blackboard

Model the task as \(p(x \mid y)\)
\(y\) : prompt
\(x\) :
response of a chatbot
Natural language conversation
Model the task as \(p(x \mid y)\)
\(y\) : prompt
\(x\) :
response of a chatbot
Text-to-3D structure generation

Figure credit: Tang, et al. LGM: Large Multi-View Gaussian Model for High-Resolution 3D Content Creation. ECCV 2024
Model the task as \(p(x \mid y)\)
\(y\) : class label
\(x\) :
generated image
Class-conditional image generation
Image generated by: Li, et al. Autoregressive Image Generation without Vector Quantization, 2024
red fox

Model the task as \(p(x \mid y)\)
\(y\) : an implicit condition
\(x\) :
generated CIFAR10-like images
“Unconditional” image generation
Images generated by: Karras, et al. Elucidating the Design Space of Diffusion-Based Generative Models, NeurIPS 2022
“images following CIFAR10 distribution”

Model the task as \(p(x \mid y)\)
\(y\) : an image as the “condition”
\(x\) : probability of classes conditioned on the image
Classification (a generative perspective)

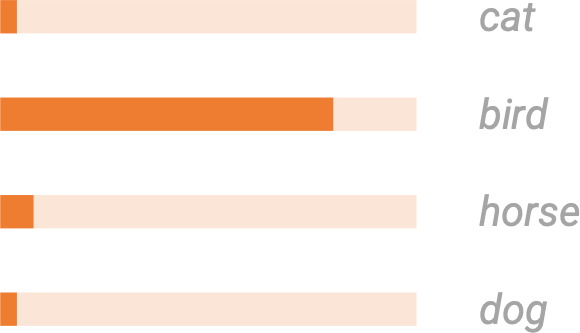
Model the task as \(p(x \mid y)\)
\(y\) : an image as the “condition”
\(x\) : plausible descriptions
conditioned on the image
Open-vocabulary recognition

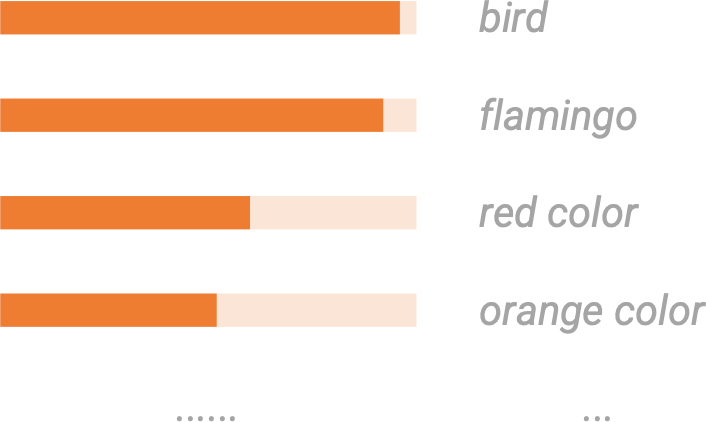
Model the task as \(p(x \mid y)\)
\(y\) : an image as the “condition”
\(x\) : plausible descriptions conditioned on the image
Image Captioning


Model the task as \(p(x \mid y)\)
\(y\) : visual and other
sensory observations
\(x\) : policies
(probability of actions)
Policy Learning in Robotics
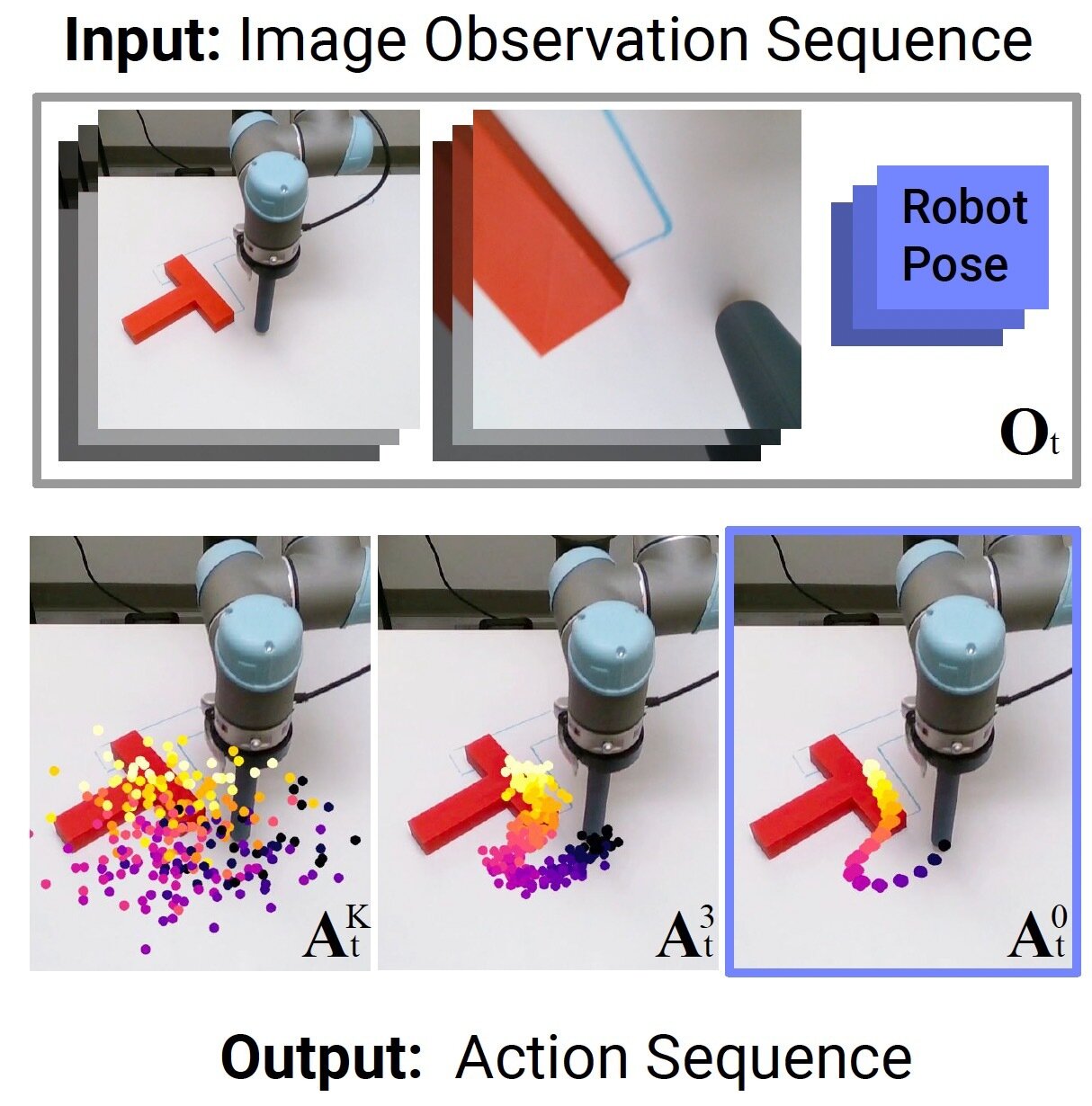

Chi, et al. Diffusion Policy: Visuomotor Policy Learning via Action Diffusion, RSS 2023
In discriminative model, modeling \(p(y \mid x)\) typically means, for any given data \(x\), find the label \(y\) that maximizes \(p(y \mid x)\)
\[\operatorname{argmax} p(y \mid x)\]
We care about the absolute/relative value of \(p(y \mid x)\) for each \(y\) given \(x\)
What do we mean by modeling \(p(x \mid y)\)
In generative model, modeling \(p(x \mid y)\) typically means, for the given conditioning \(y\), synthesize / sample data \(x\) following \(p(x \mid y)\)
- We don't want to only get the mode \(\operatorname{argmax} p(x \mid y)\)
- We care less about the exact value of \(p(x \mid y)\)
- Generative models that can estimate \(p(x \mid y)\) is called "explicit generative models"
- Generative models that do not directly estimate \(p(x \mid y)\) is called "implicit generative models"
What do we mean by modeling \(p(x \mid y)\)
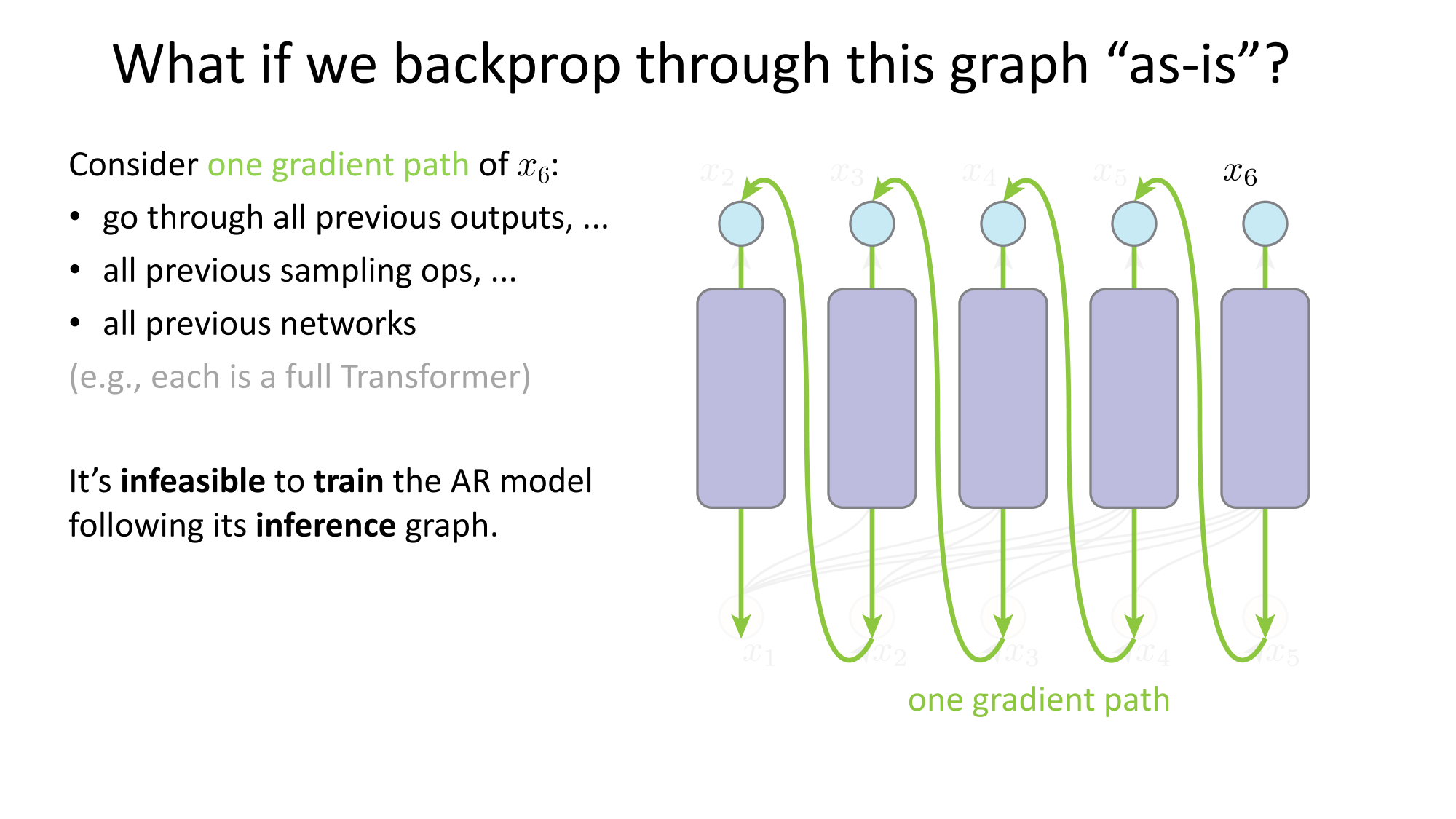
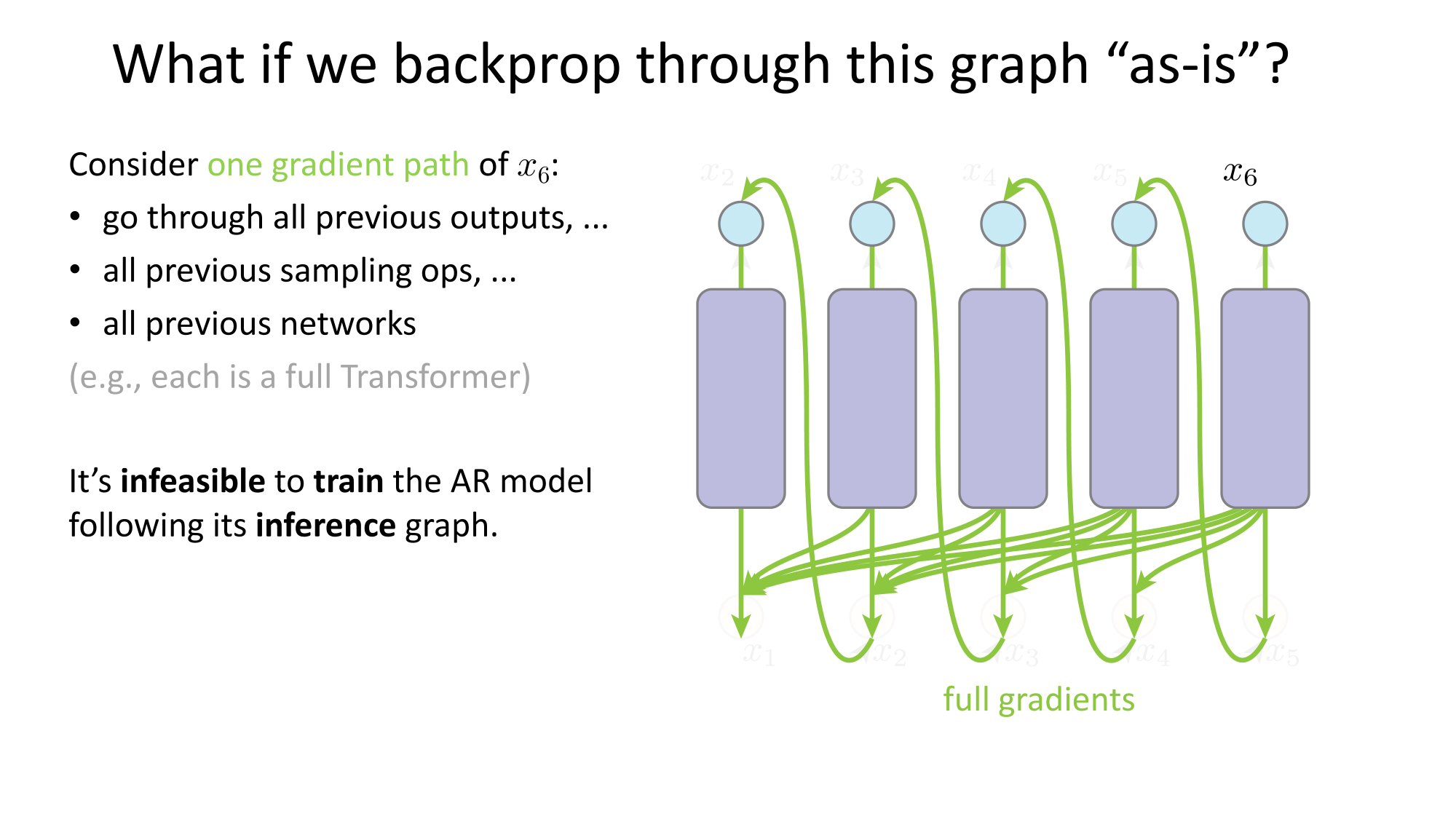
Why is this hard?
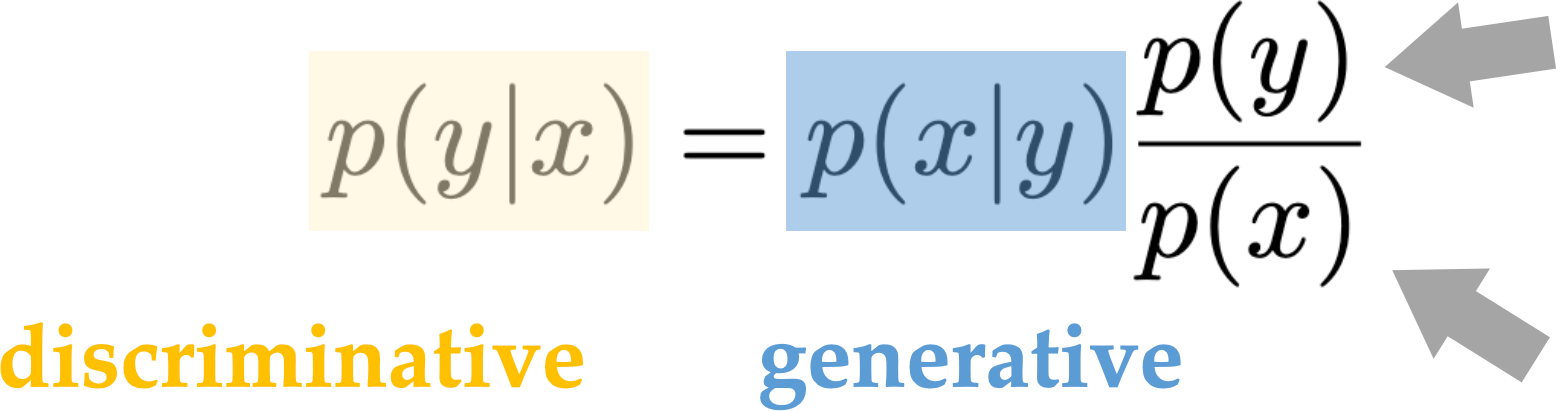
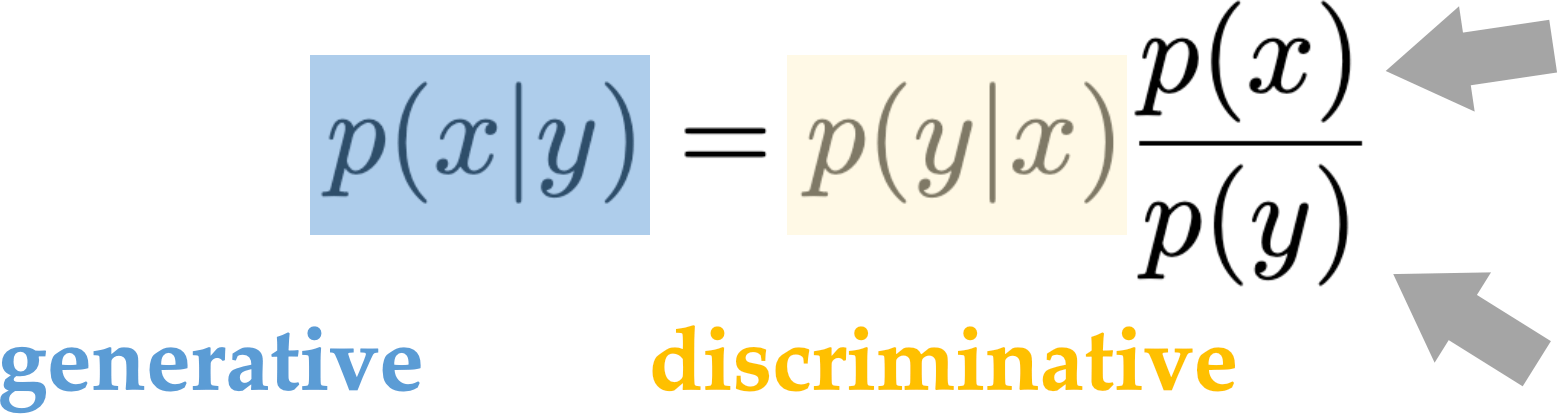
constant for given \(x\)
assuming known prior over the label \(y\)
still need to model prior distribution of \(x\)
constant for given \(y\)
Can discriminative models be generative?
Can discriminative models be generative?
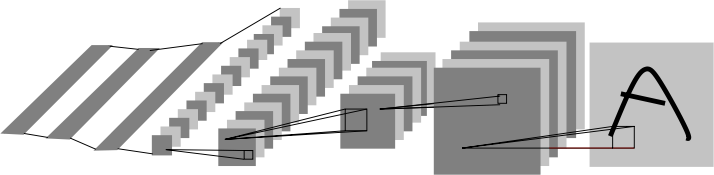
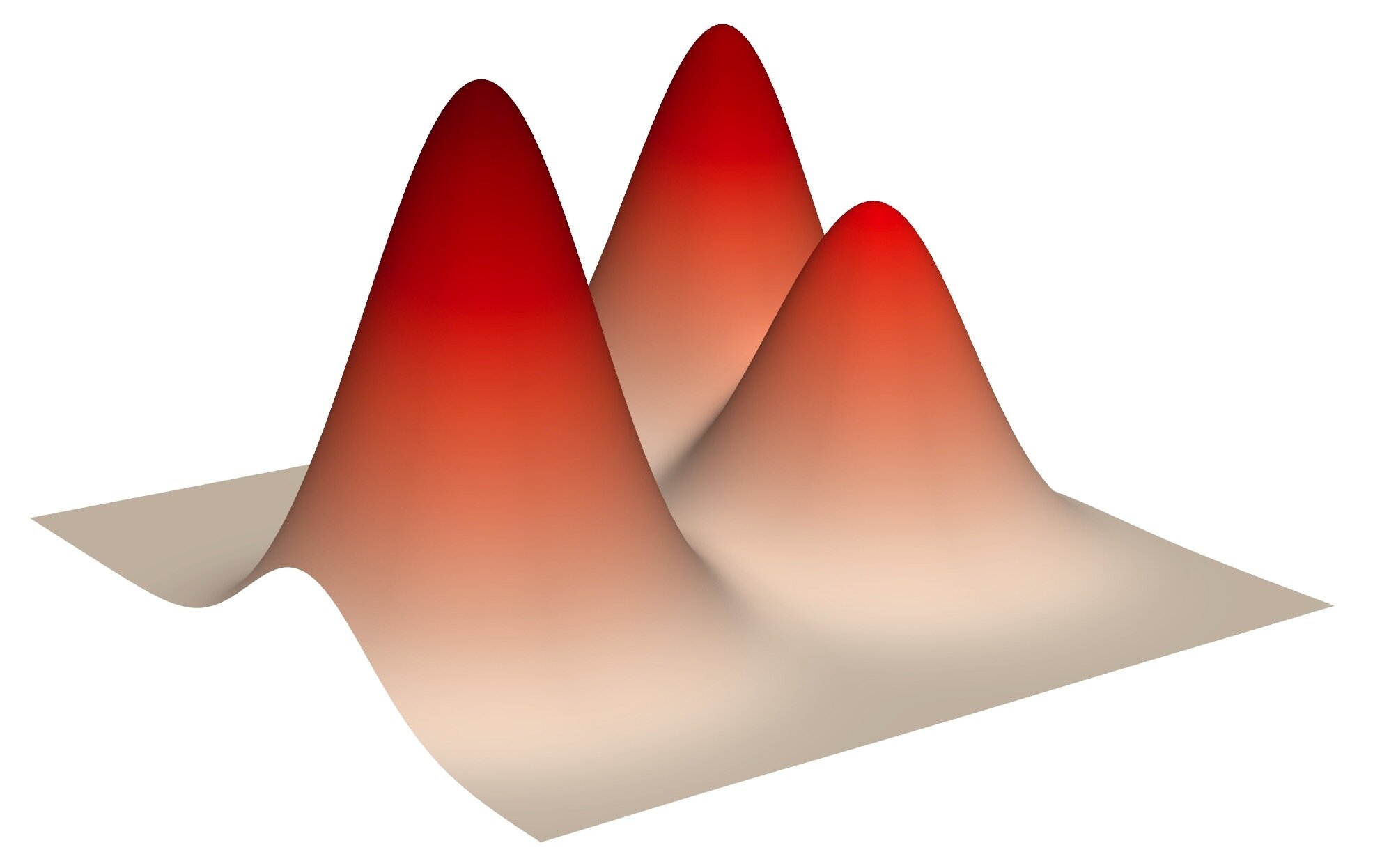
Learning to represent probabilistic distributions
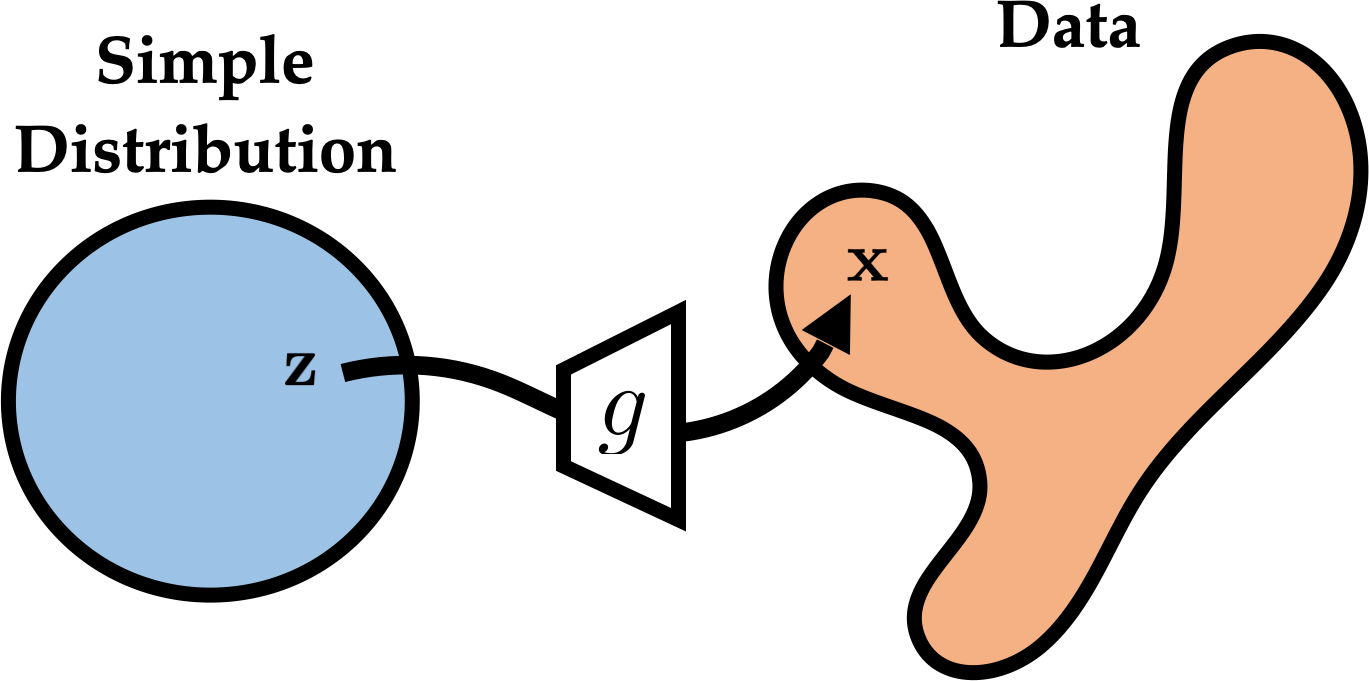
\(z \sim \pi\)
to approximate \(p_x\)
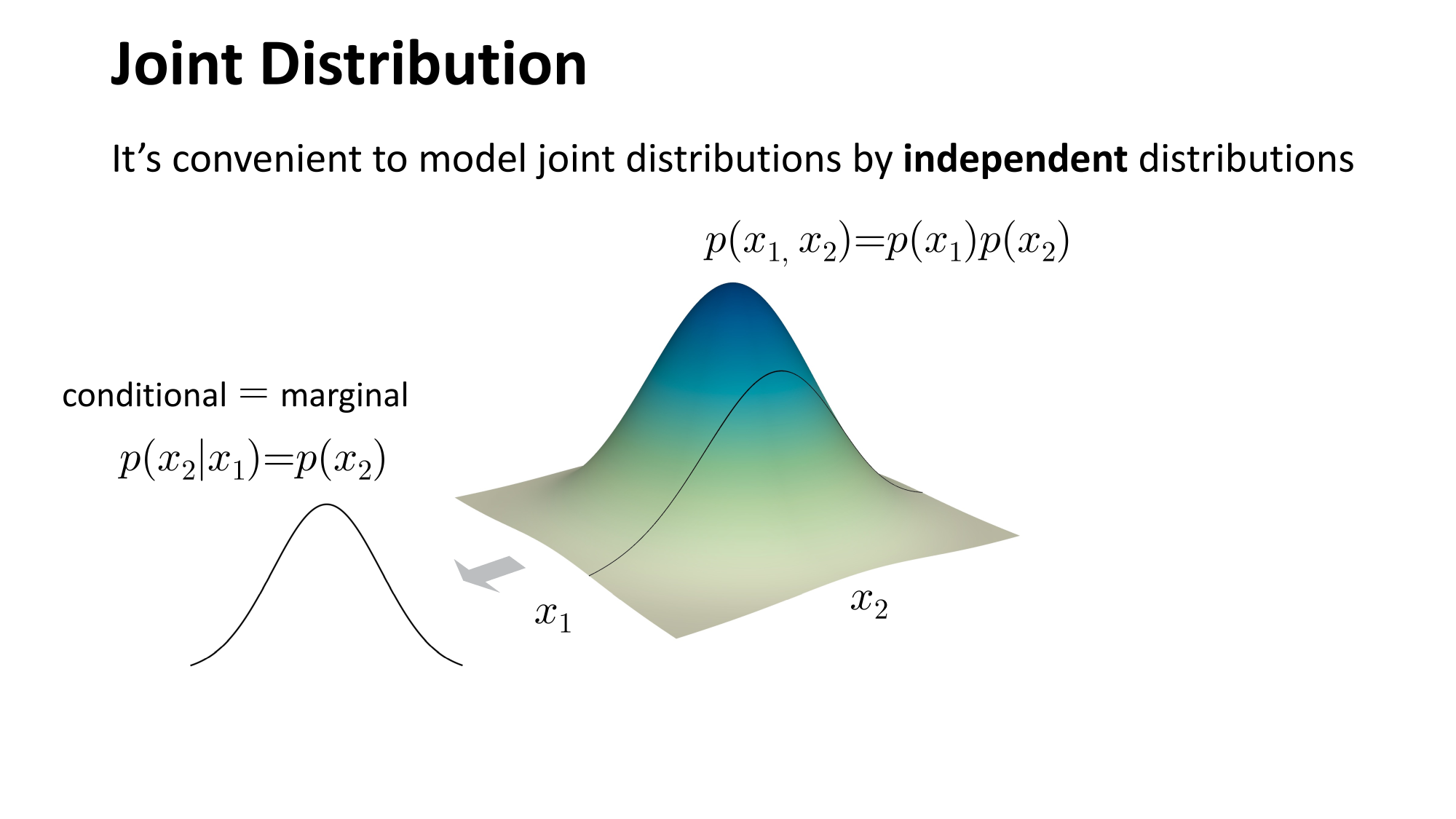
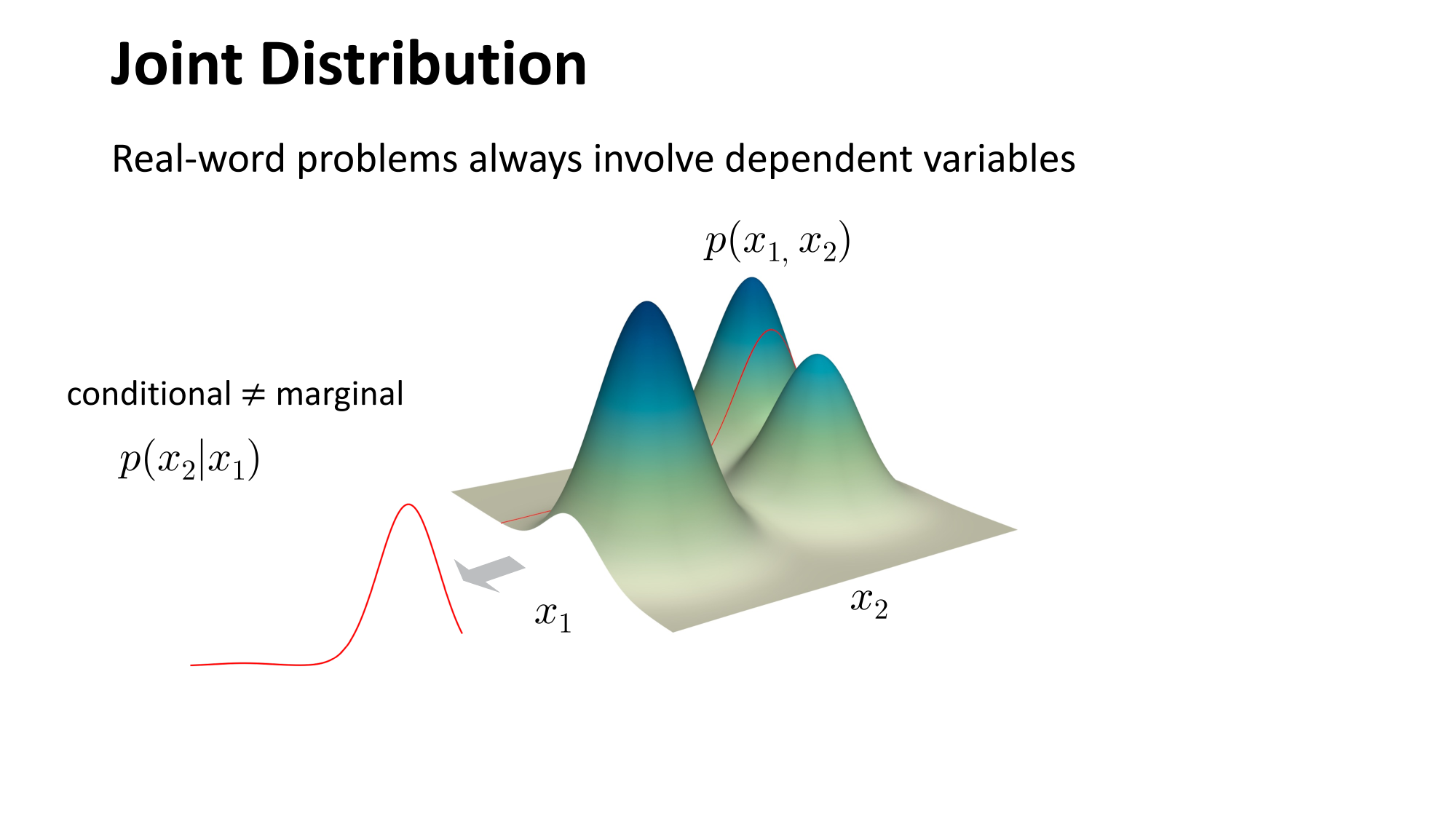
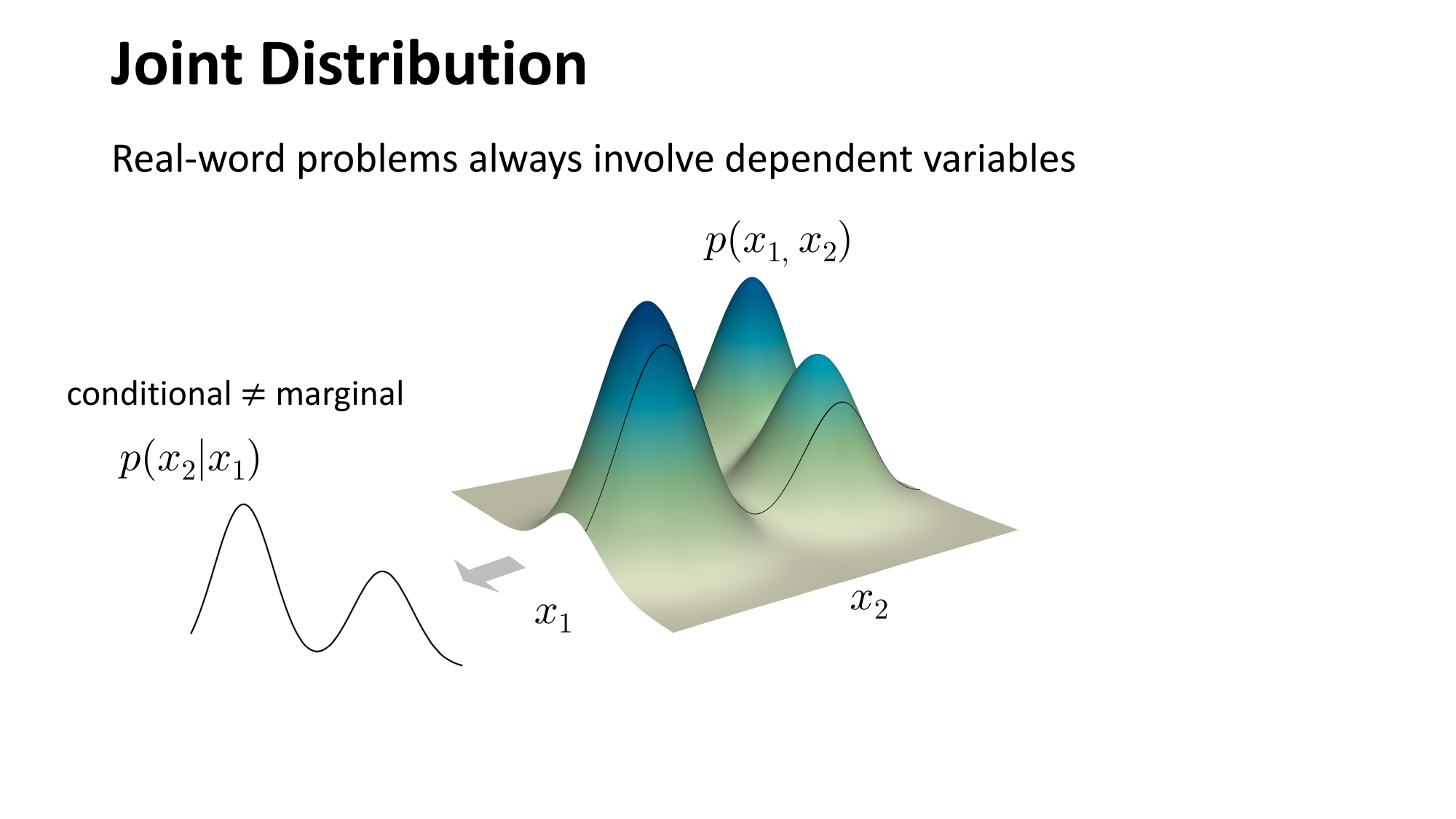
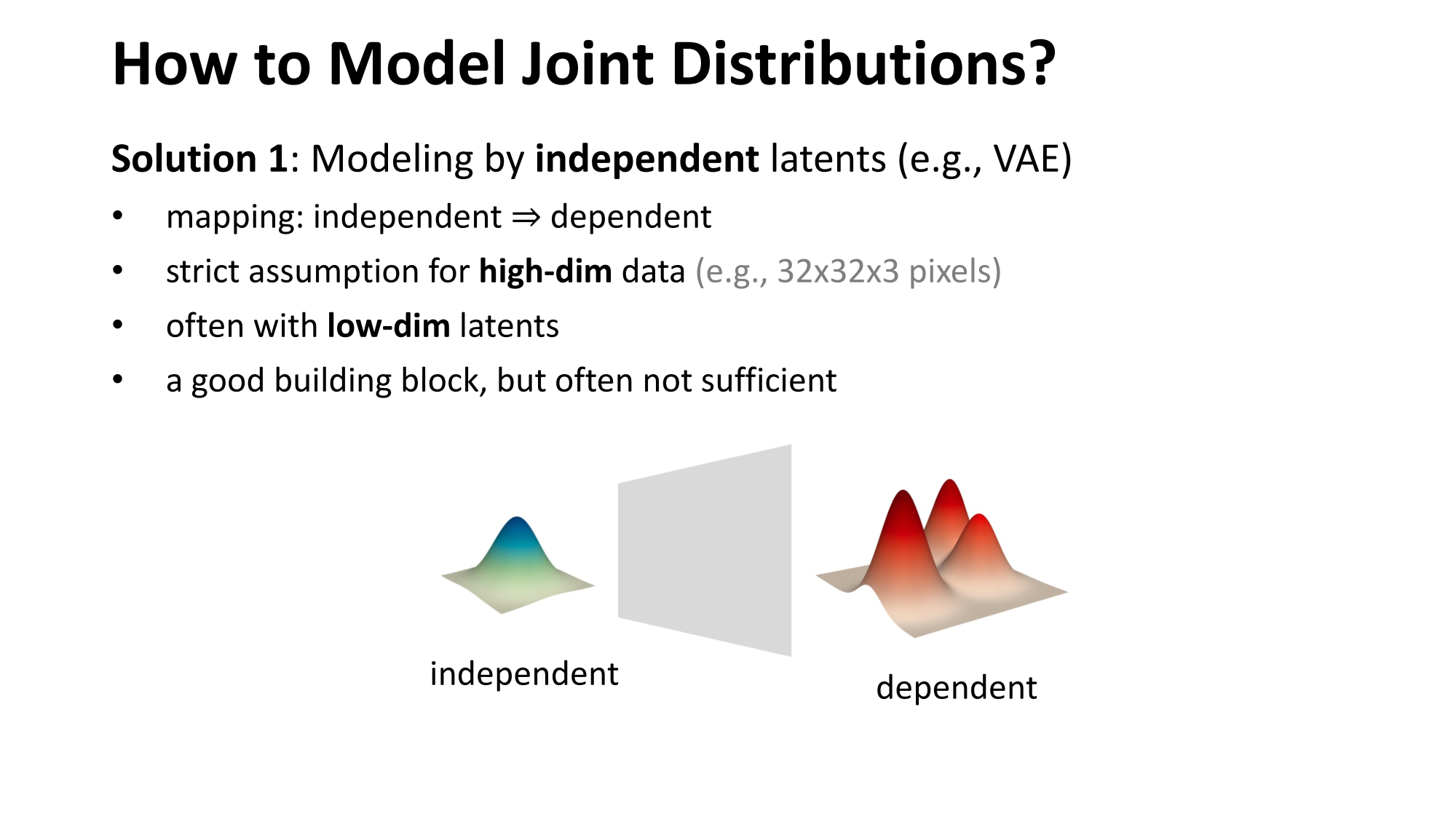
- Modeling high-dimensional distribution is always hard \(p(x)=p\left(x_1, x_2, \ldots, x_{hwc}\right)\)
- Modeling low-dimensional distribution is easy: discriminative model!
- Can we convert the problem of modeling high-dimensional distribution into modeling low-dimensional distribution?




image depth (channels)
image width
image
height
Learning to represent probabilistic distributions








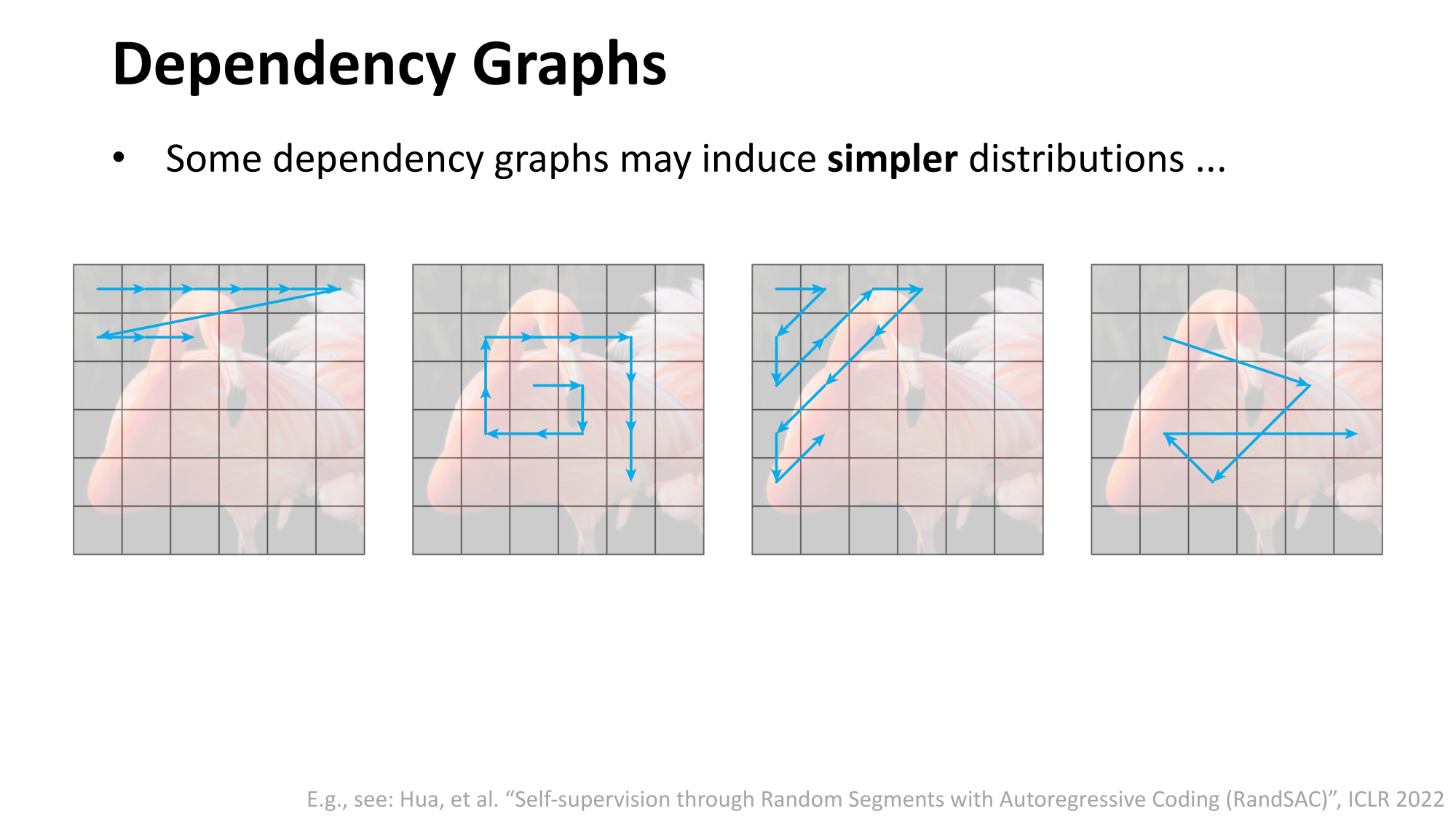

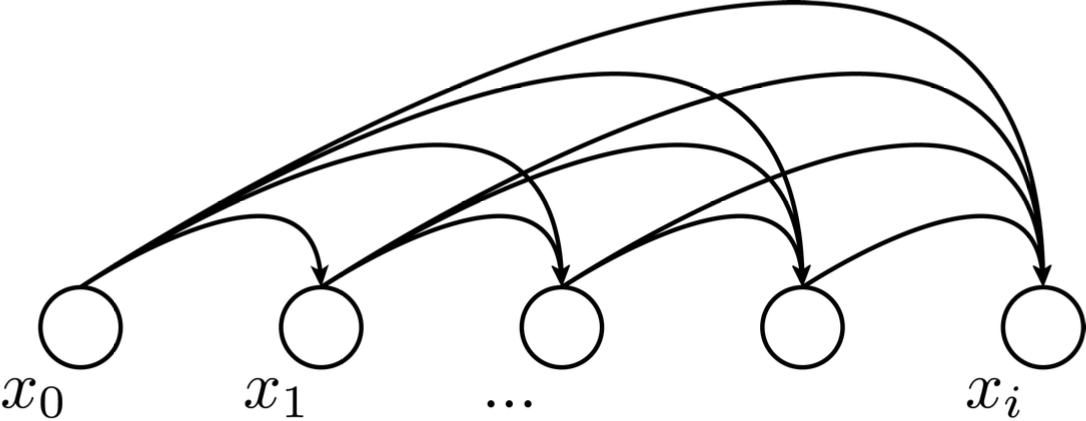
this dependency graph is what engineers designed (not learned)
Not all parts of the learned distribution modeling is done by learning
e.g. auto-regressive model
Not all parts of the learned distribution modeling is done by learning
e.g. auto-regressive model
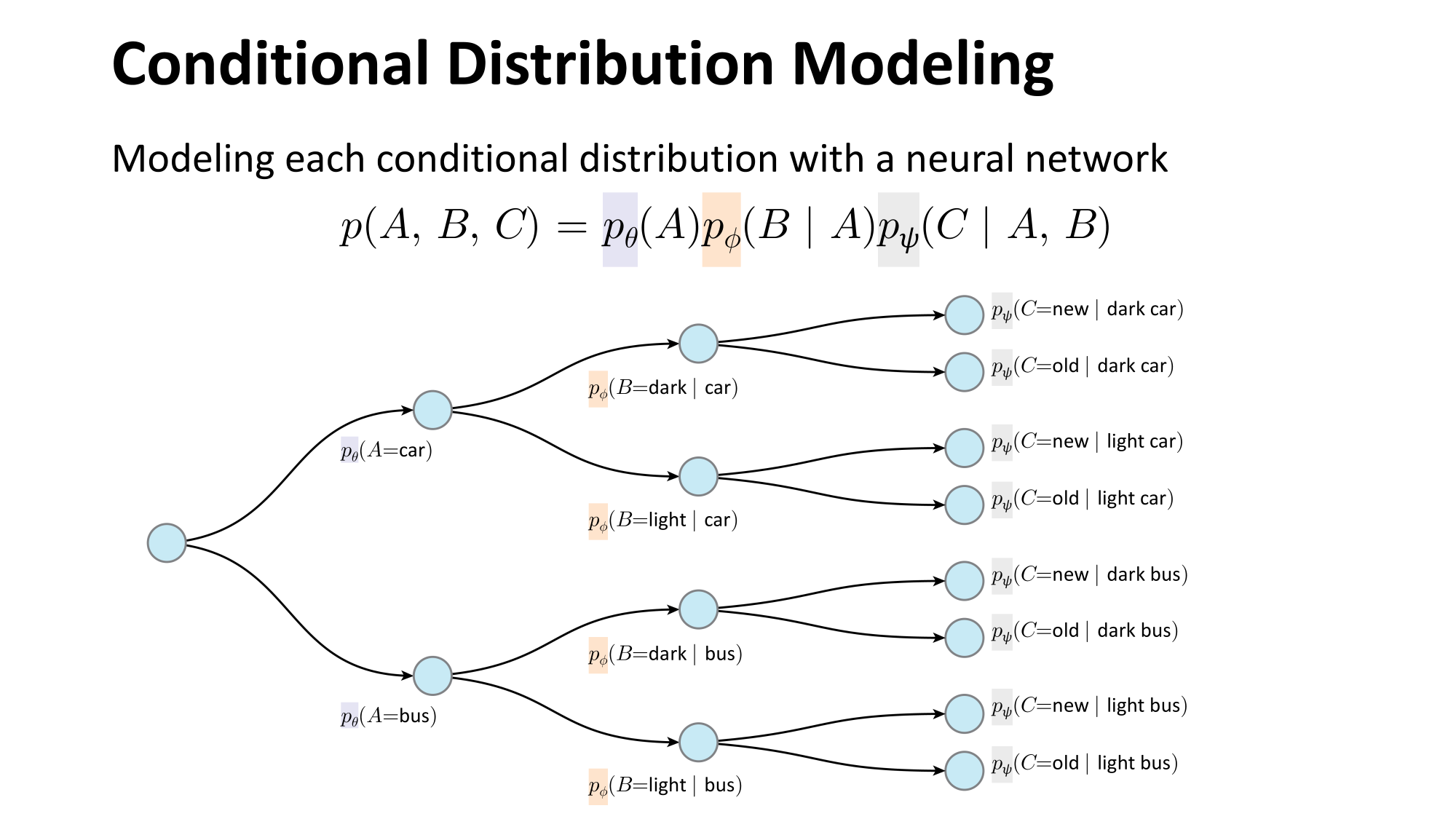
these function mappings are learned (via various hypothesis class choices)
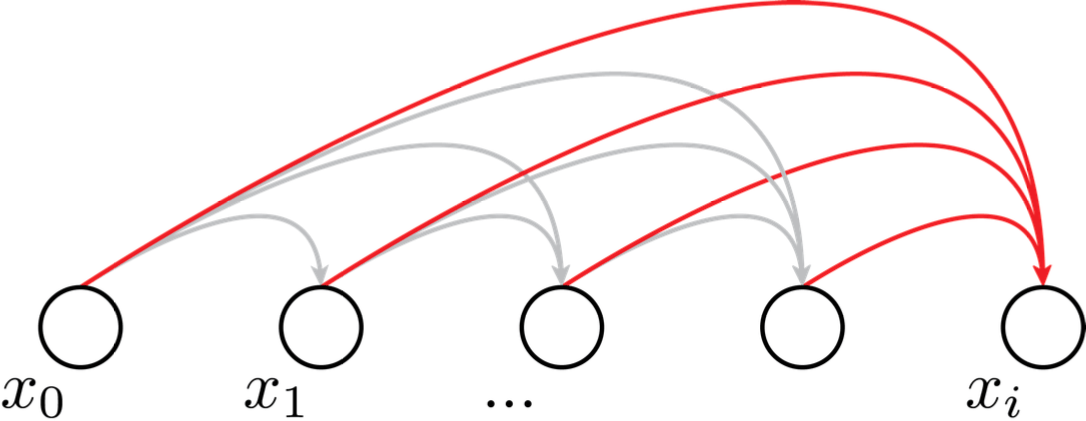
this dependency graph is what engineers designed (not learned)
Not all parts of the learned distribution modeling is done by learning
e.g. diffusion model
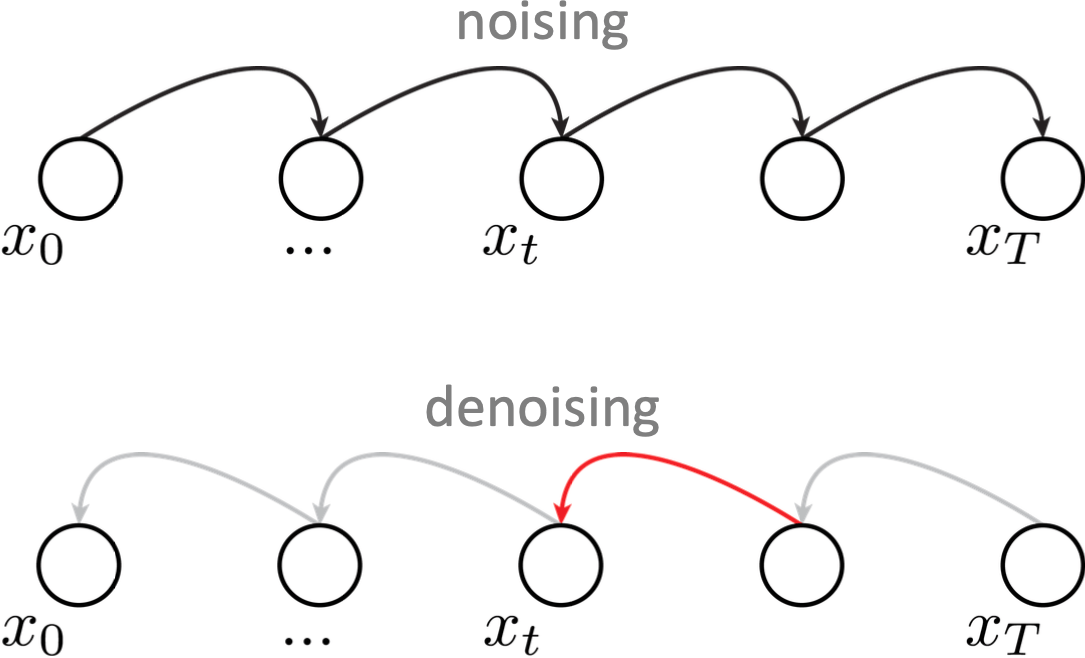
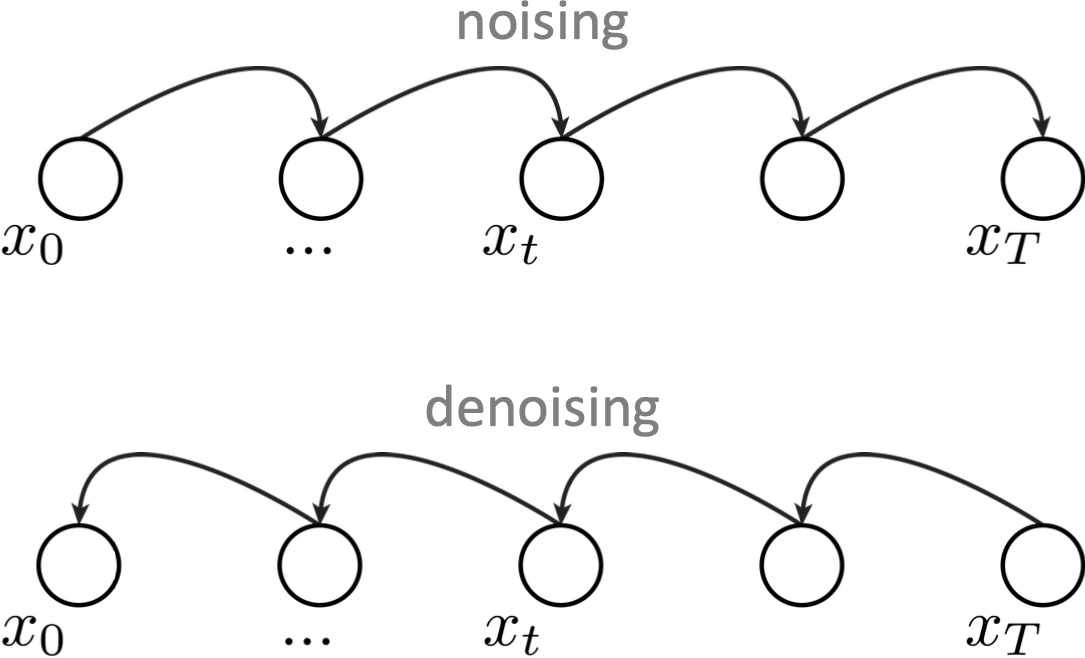
Not all parts of the learned distribution modeling is done by learning
e.g. diffusion model
these function mappings are learned (via various hypothesis class choices)

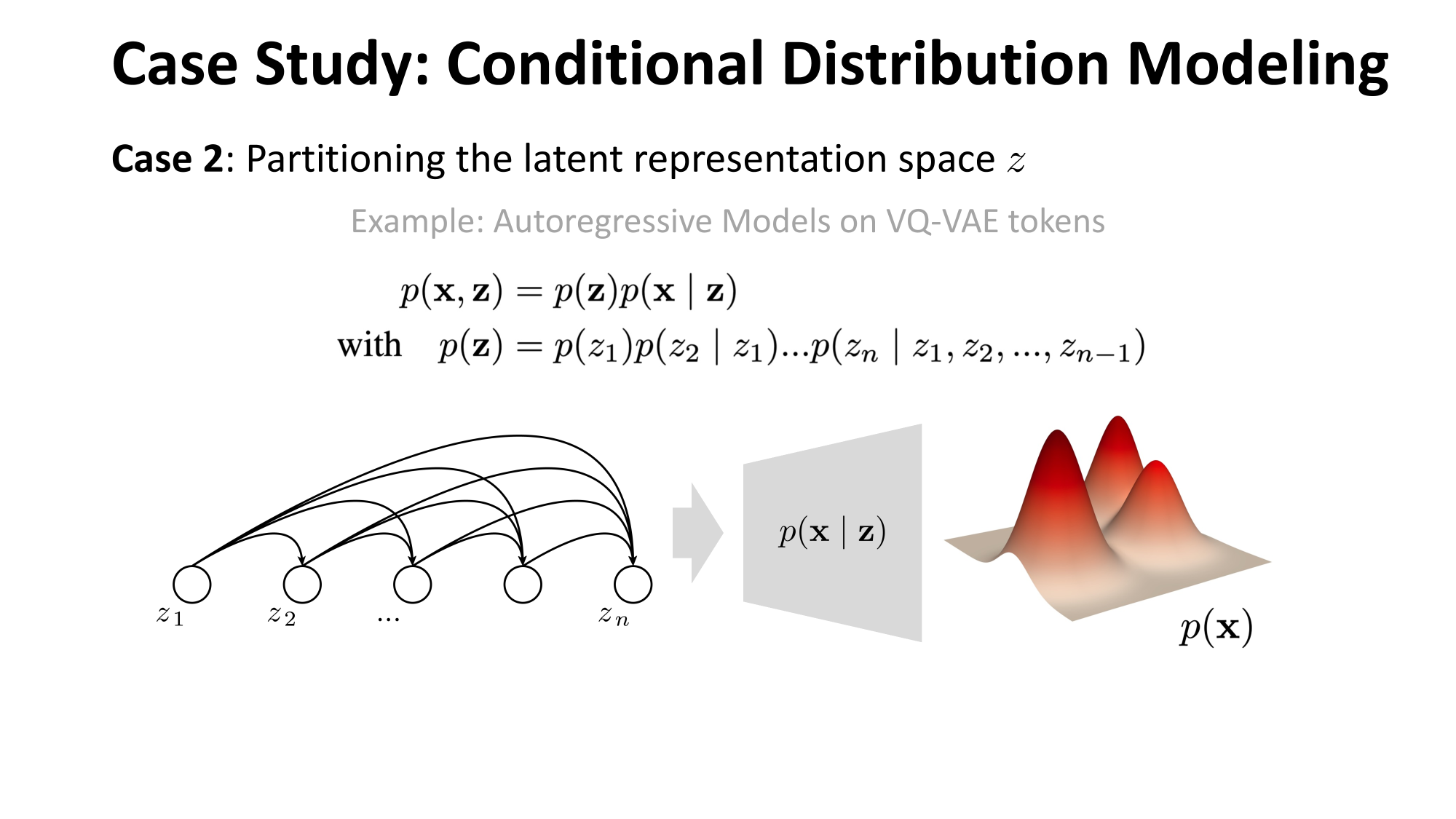




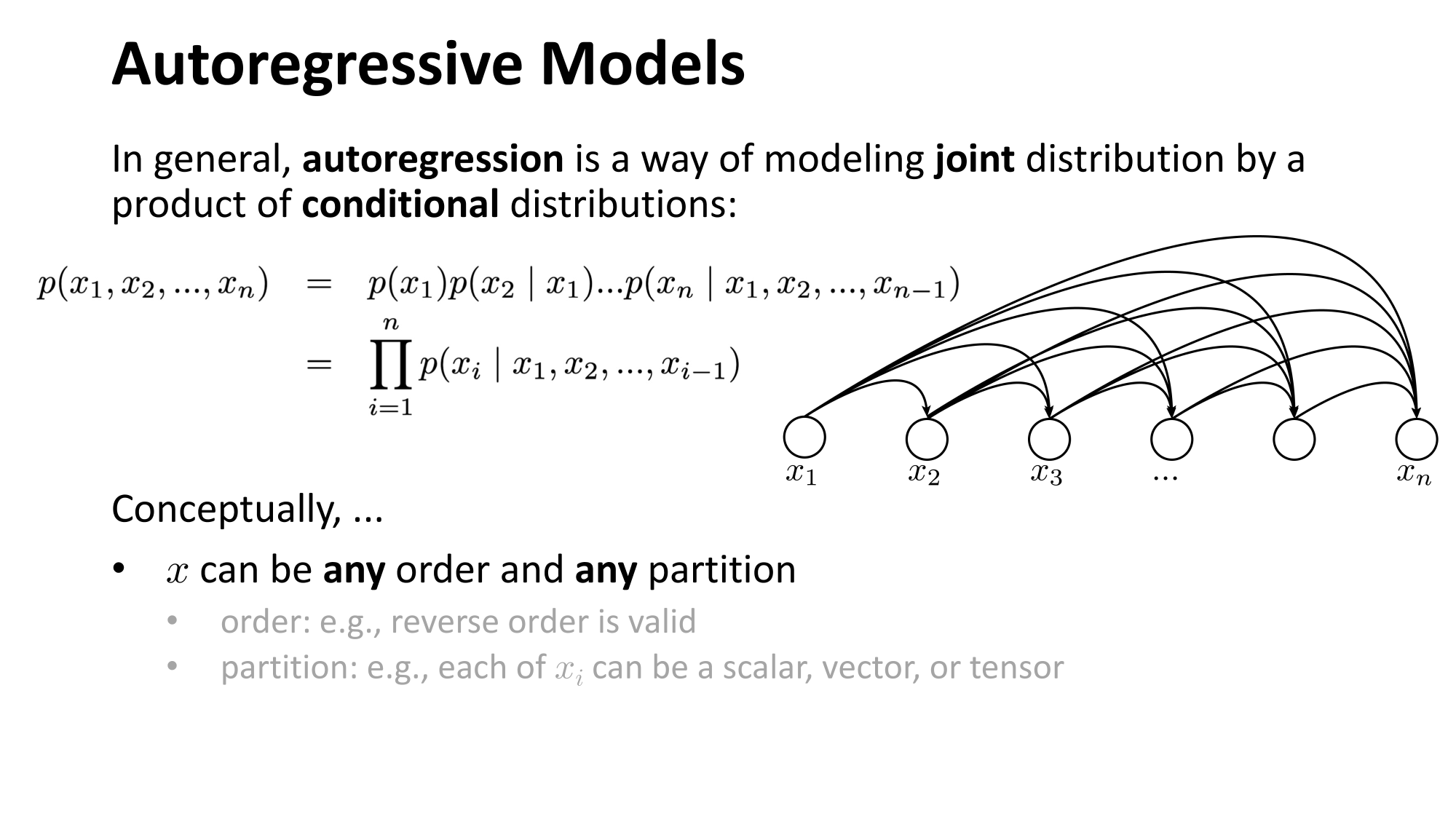

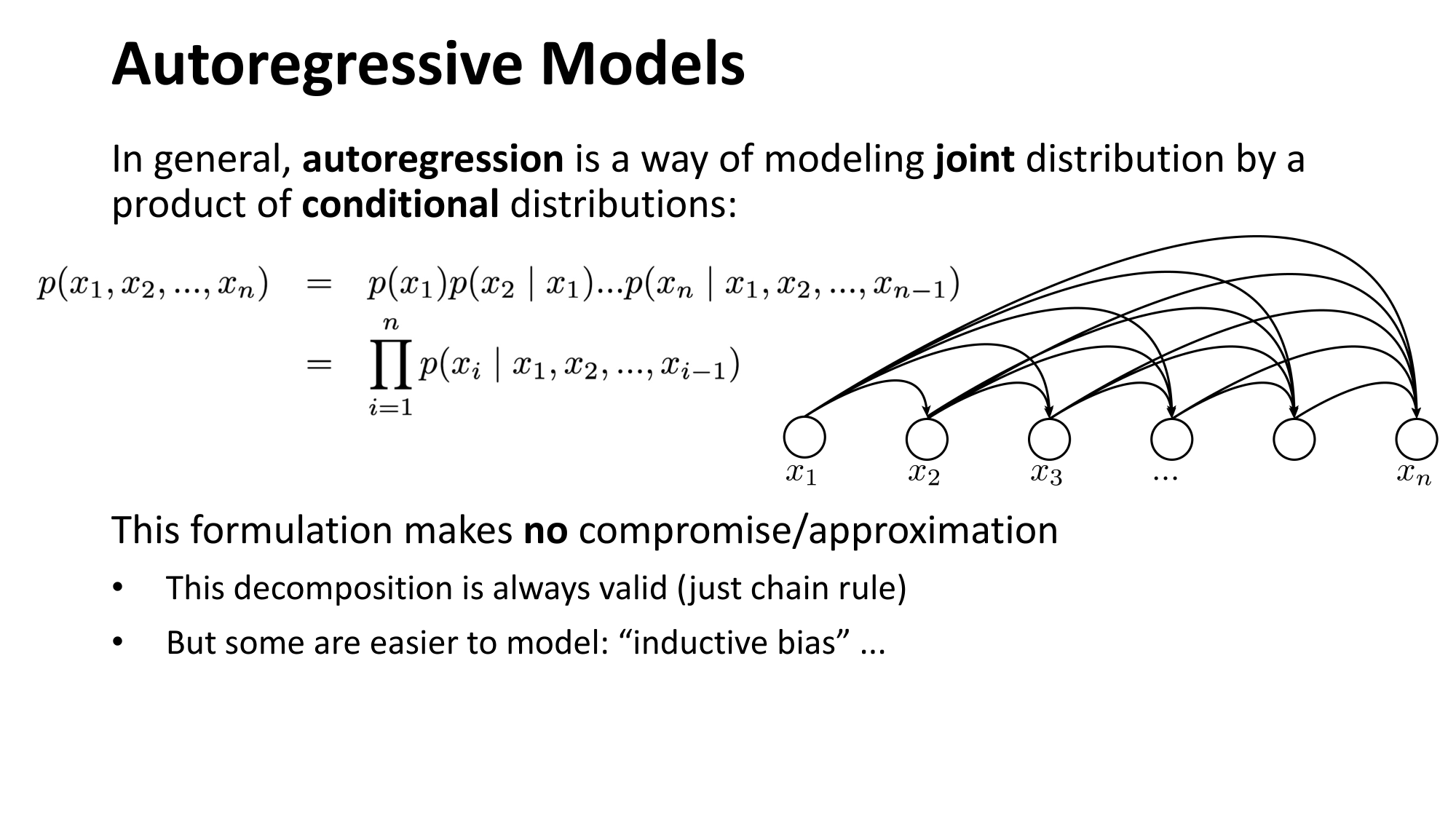
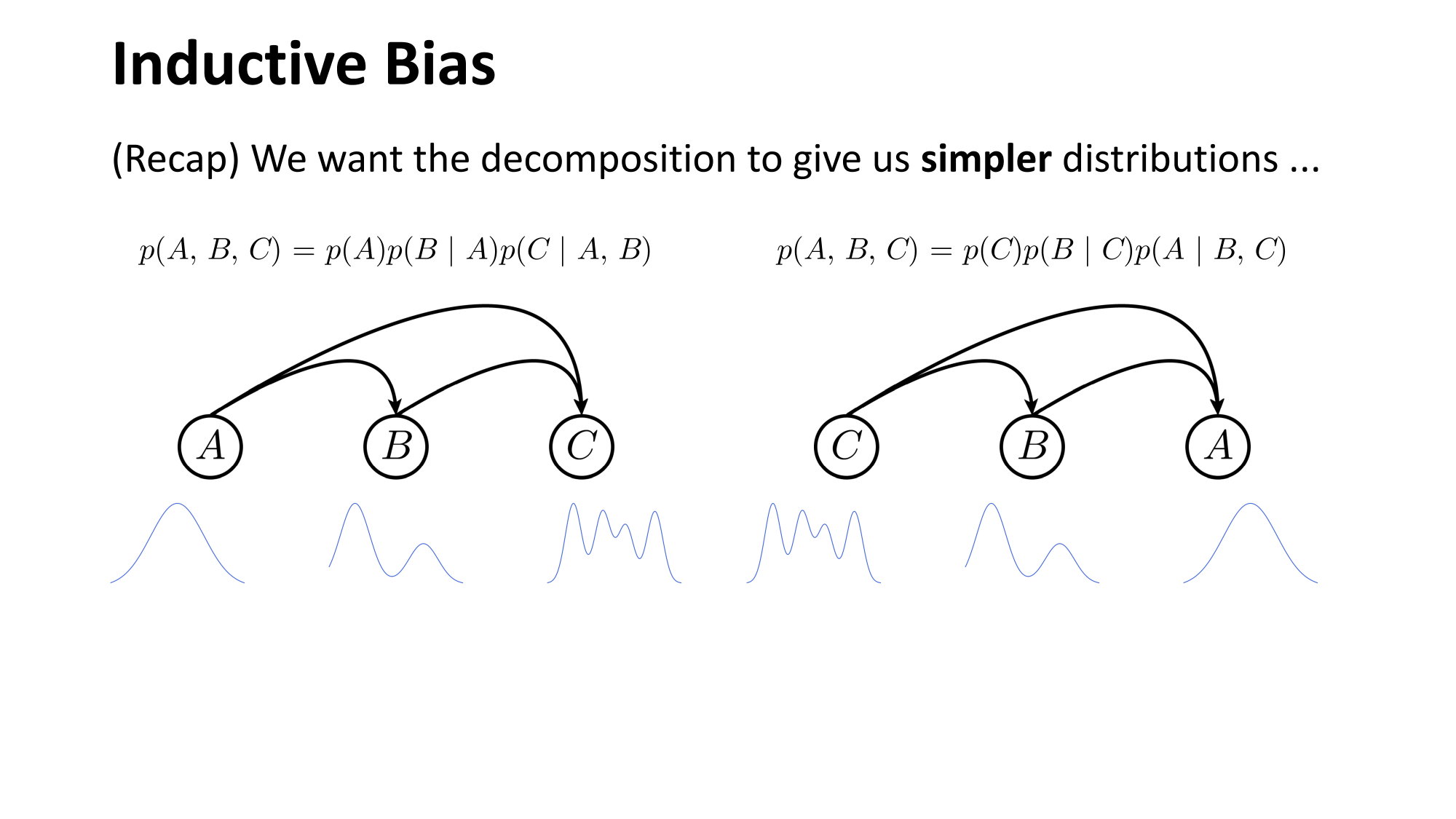

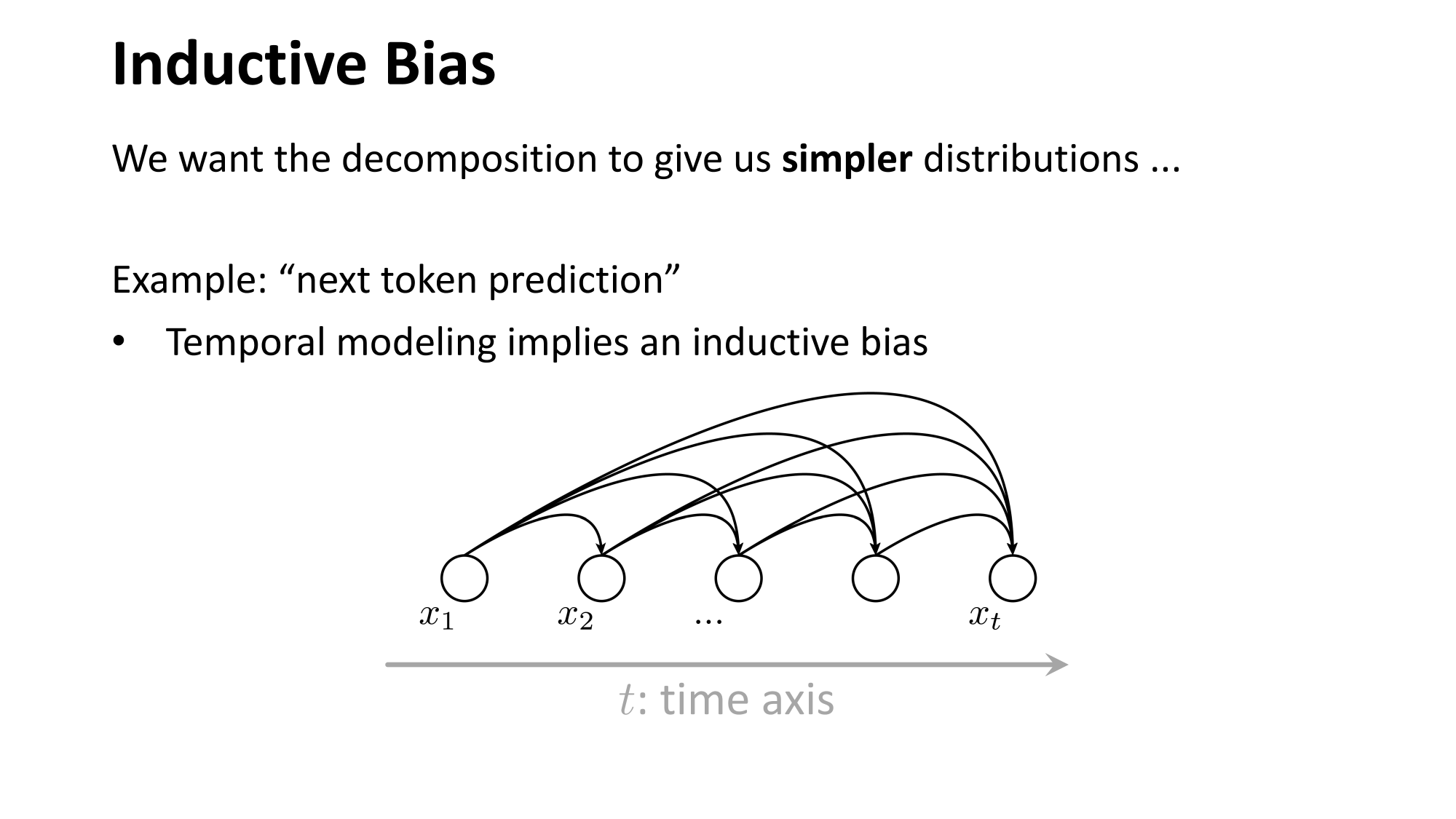




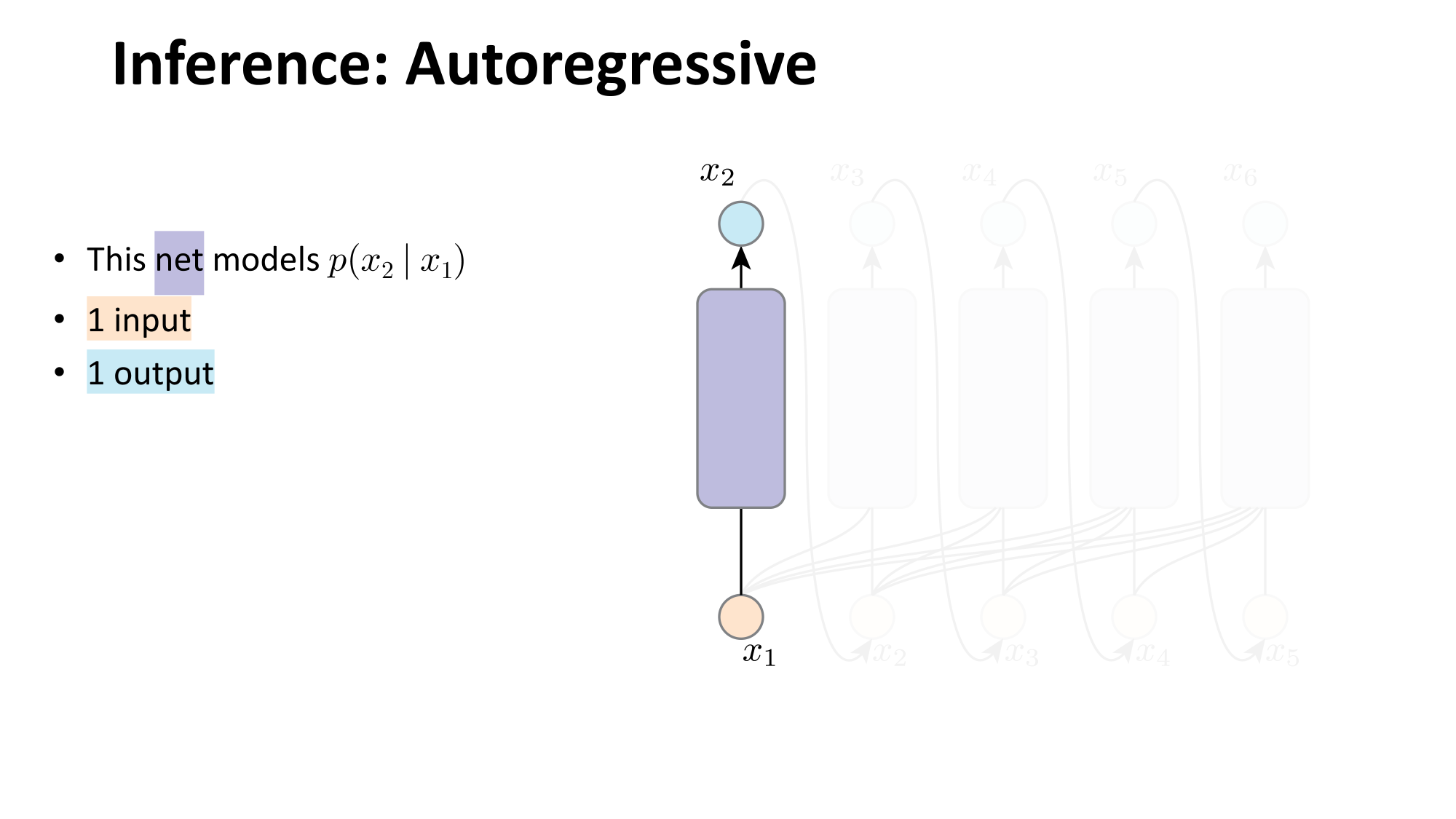
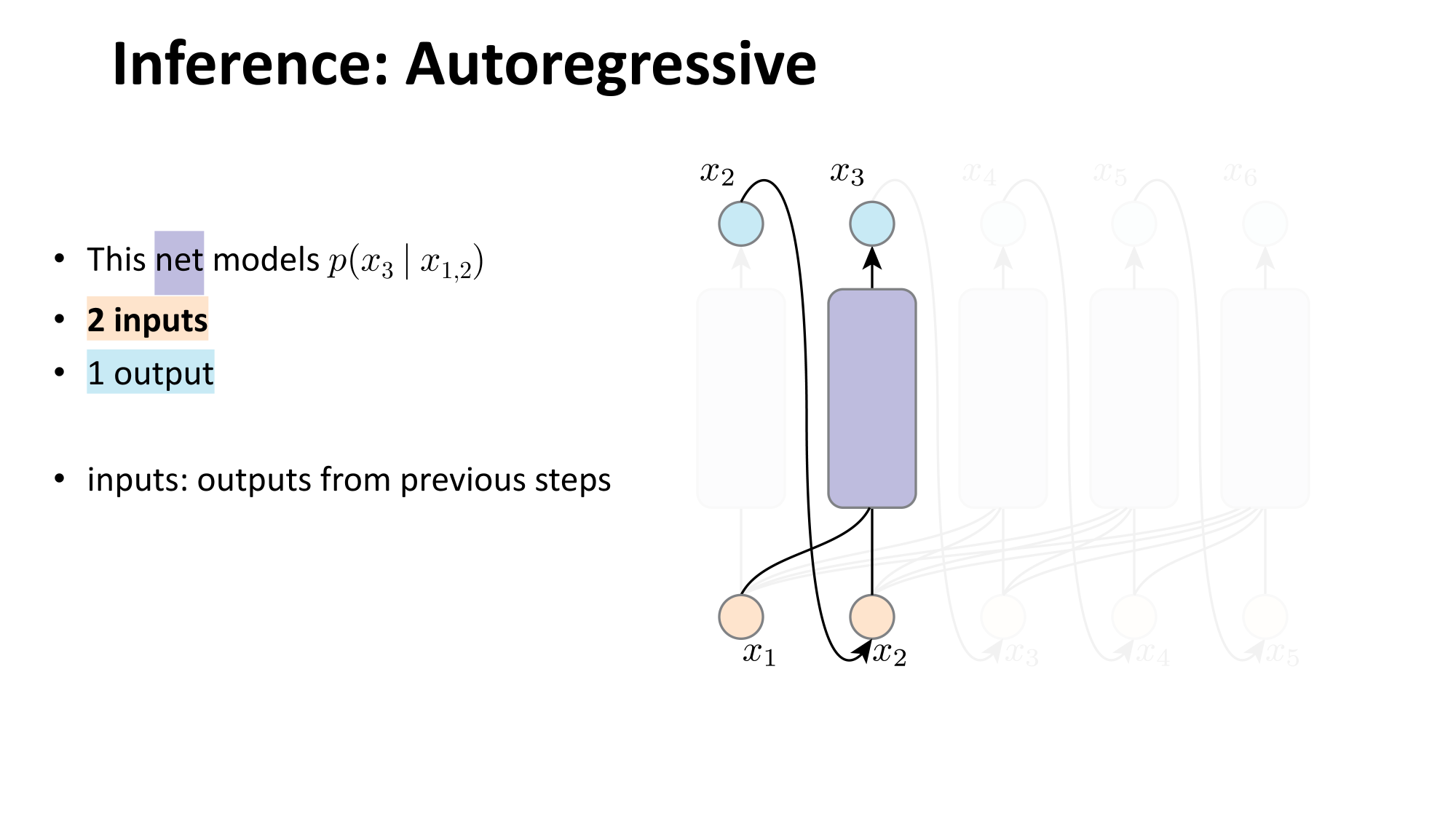
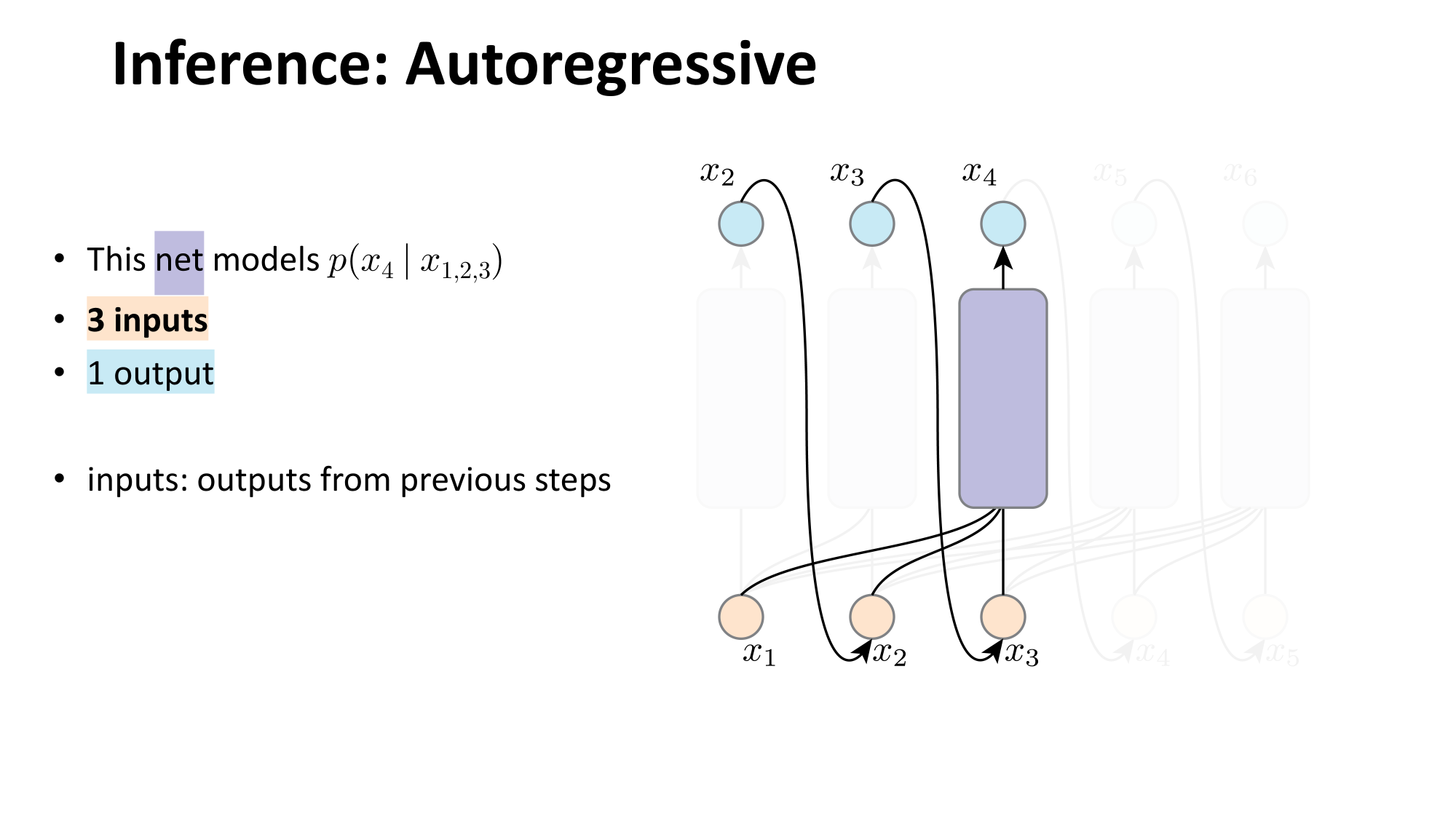
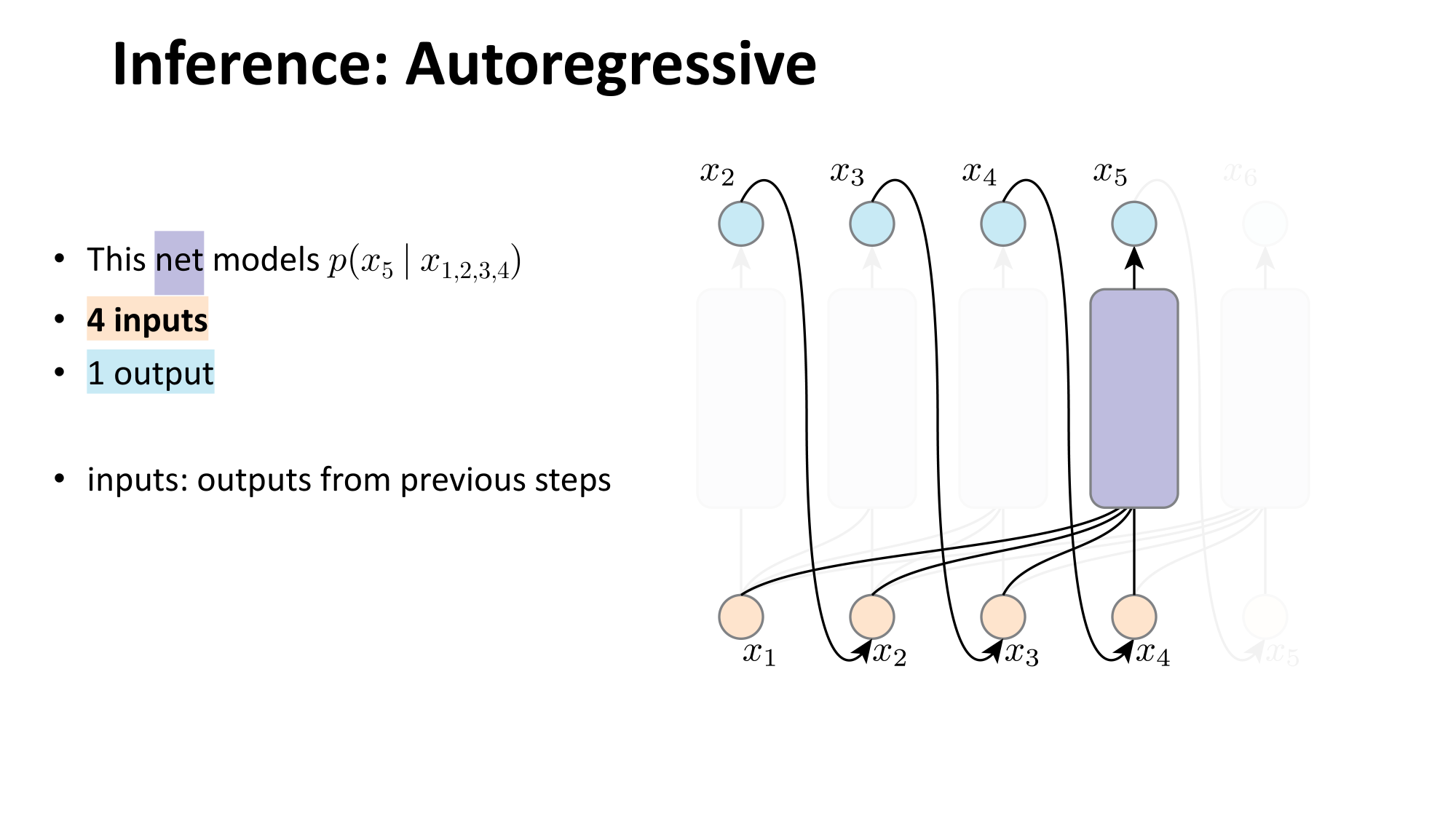
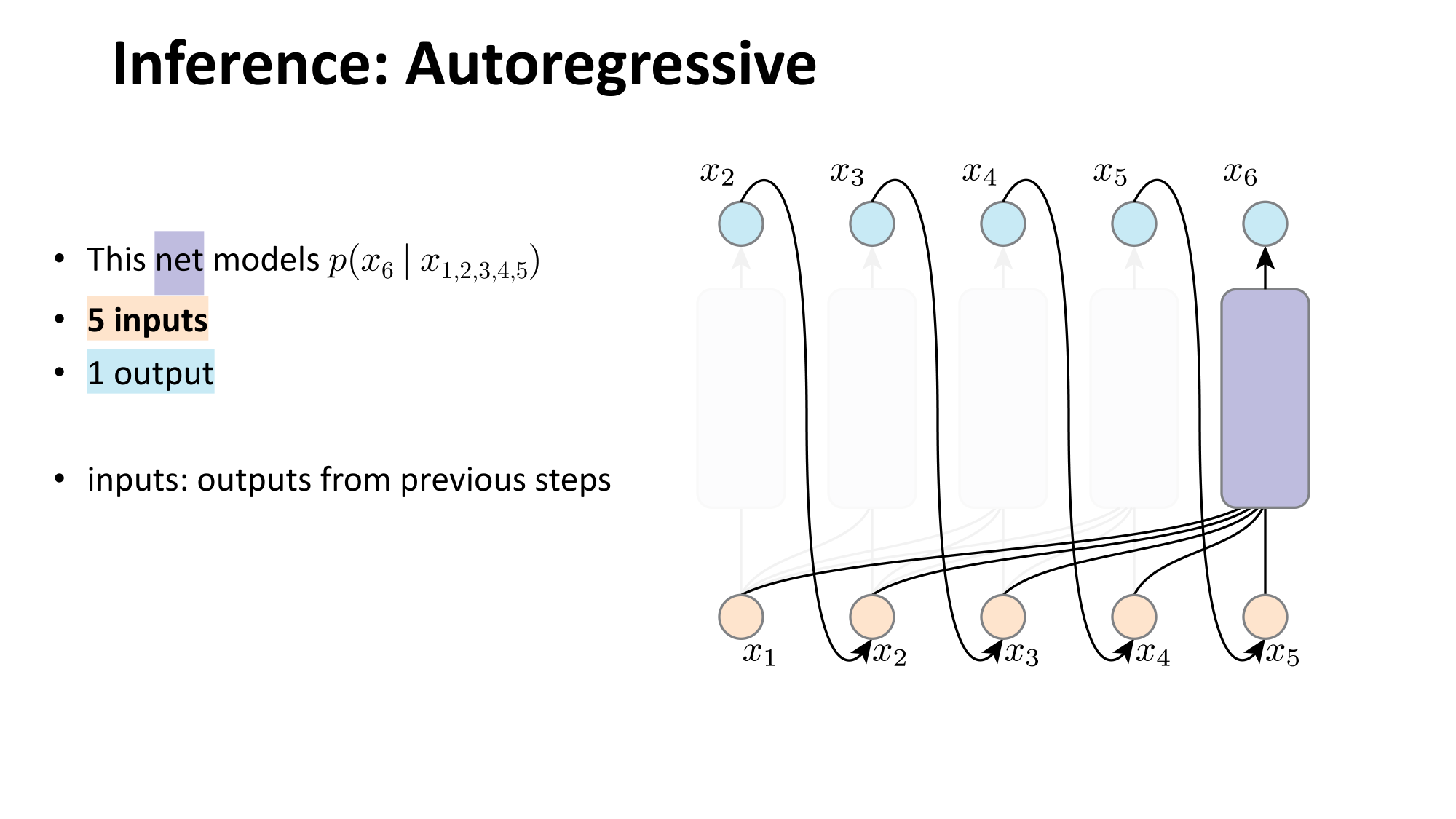
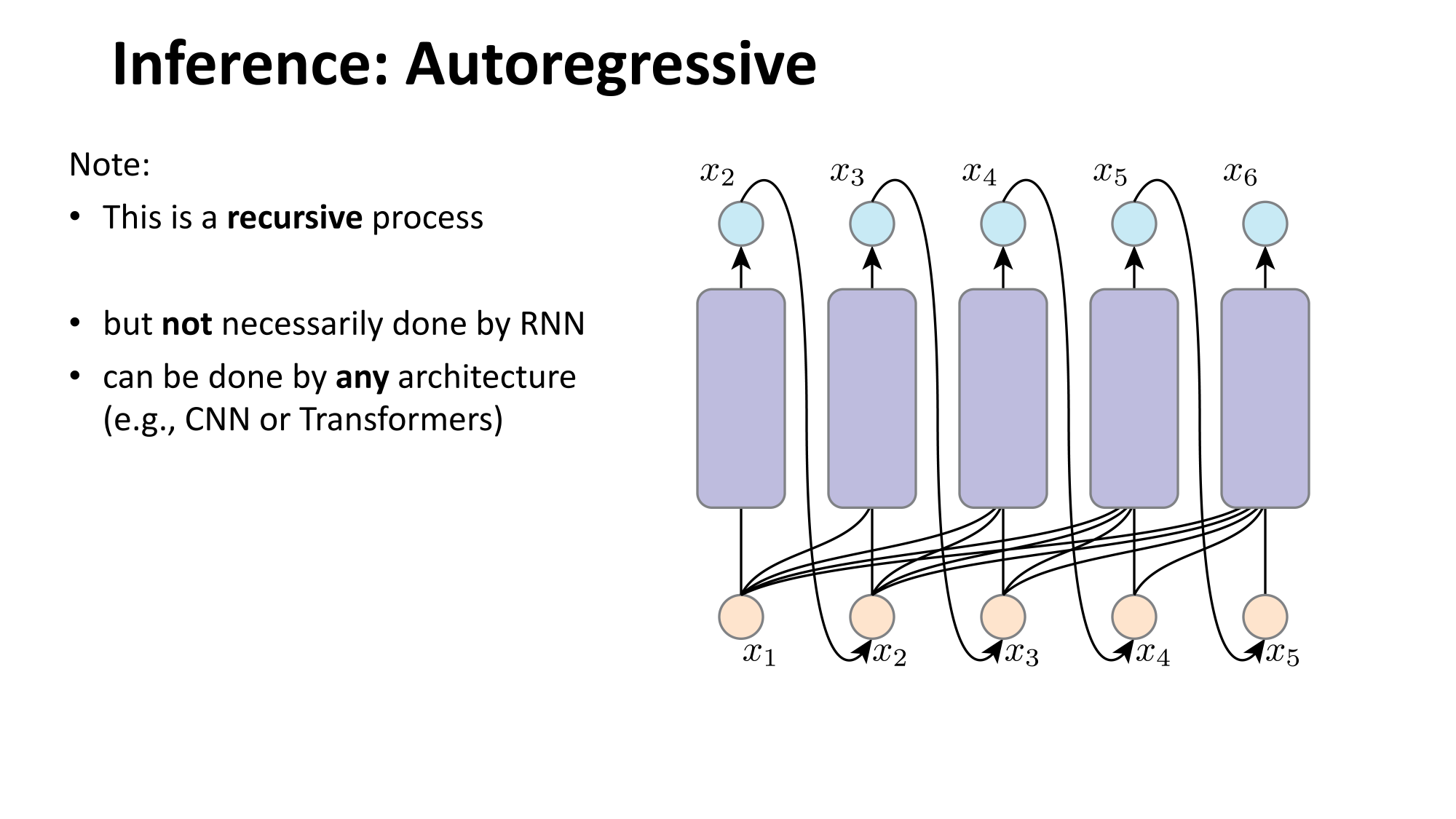




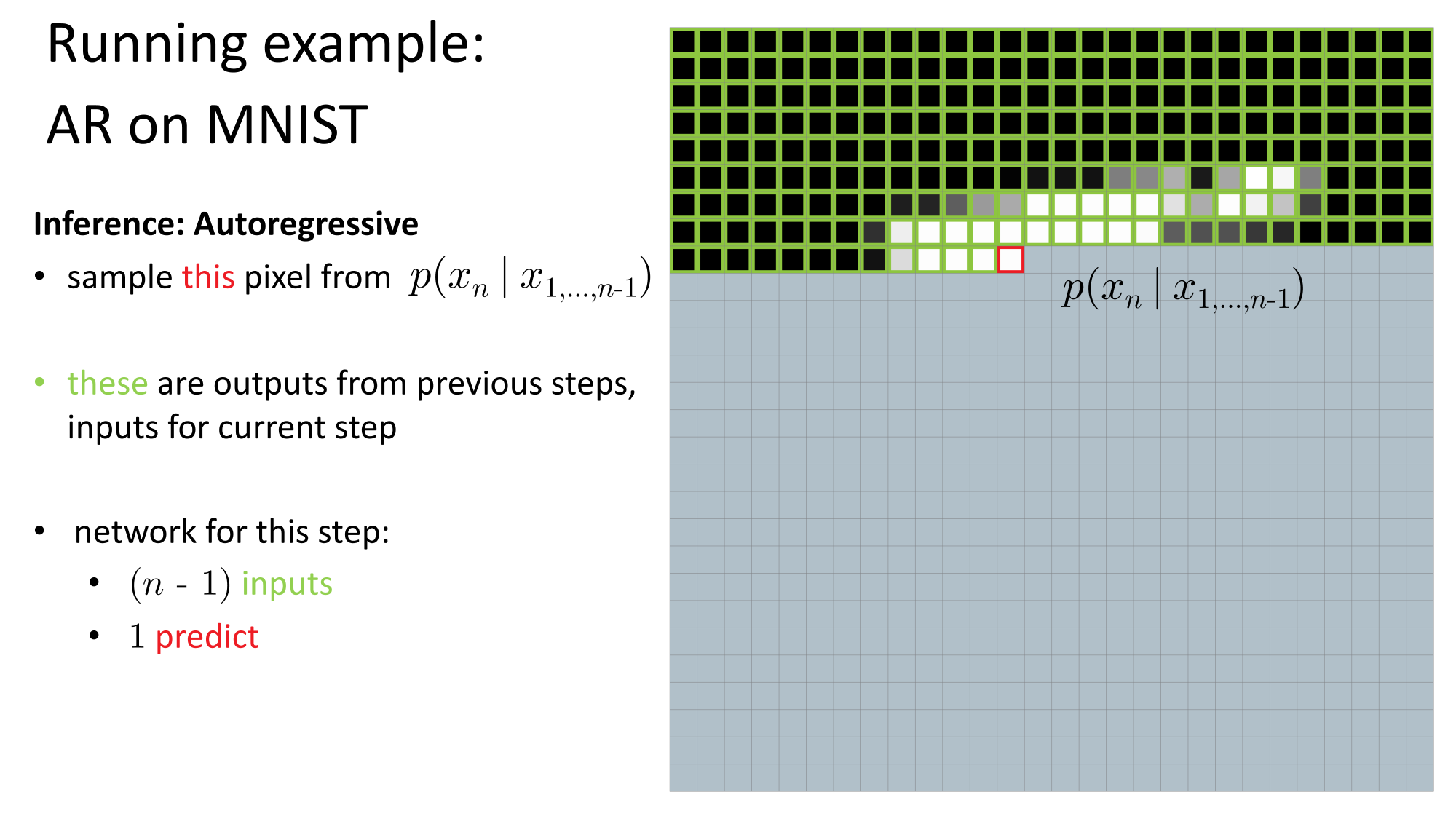
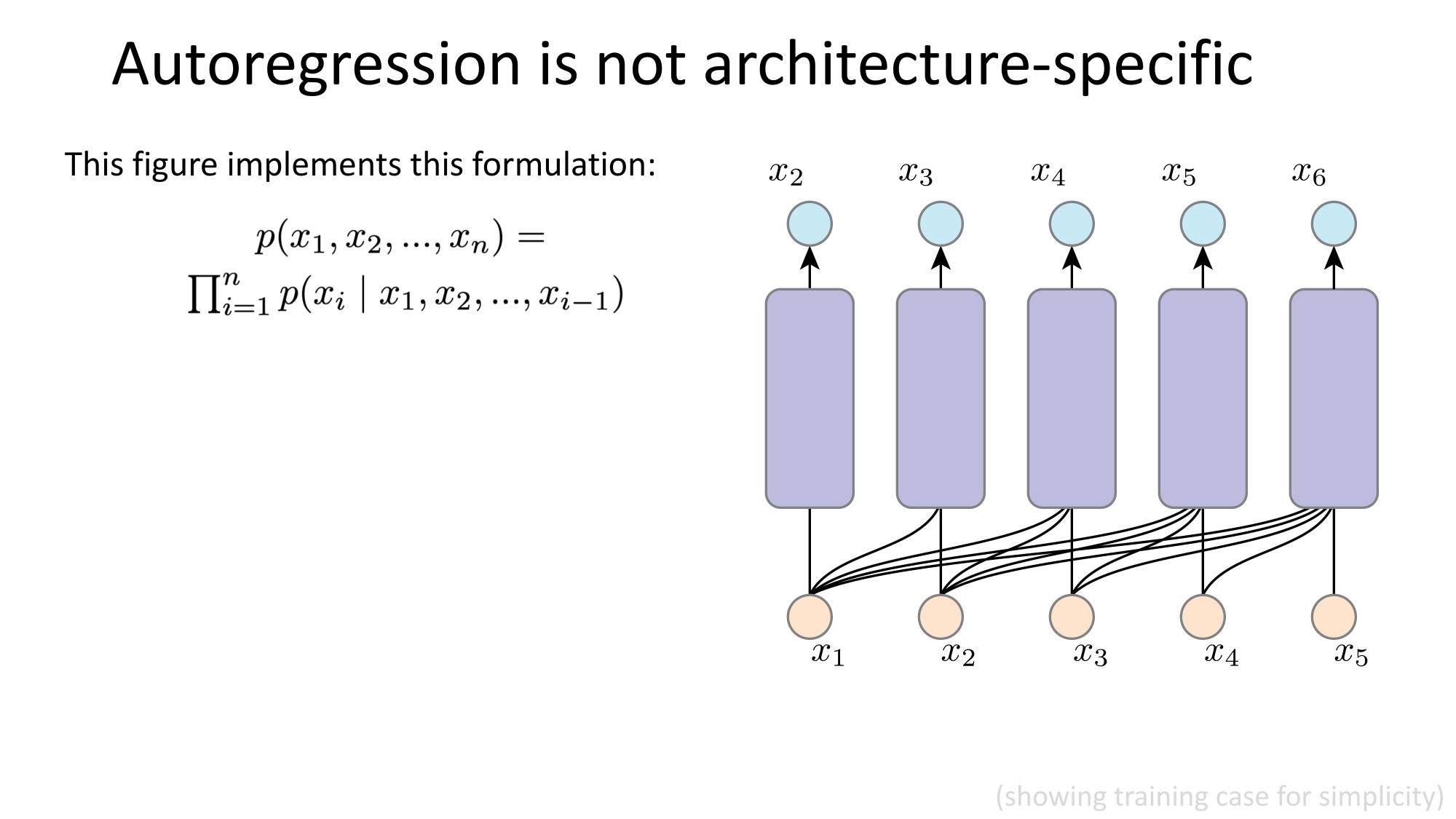
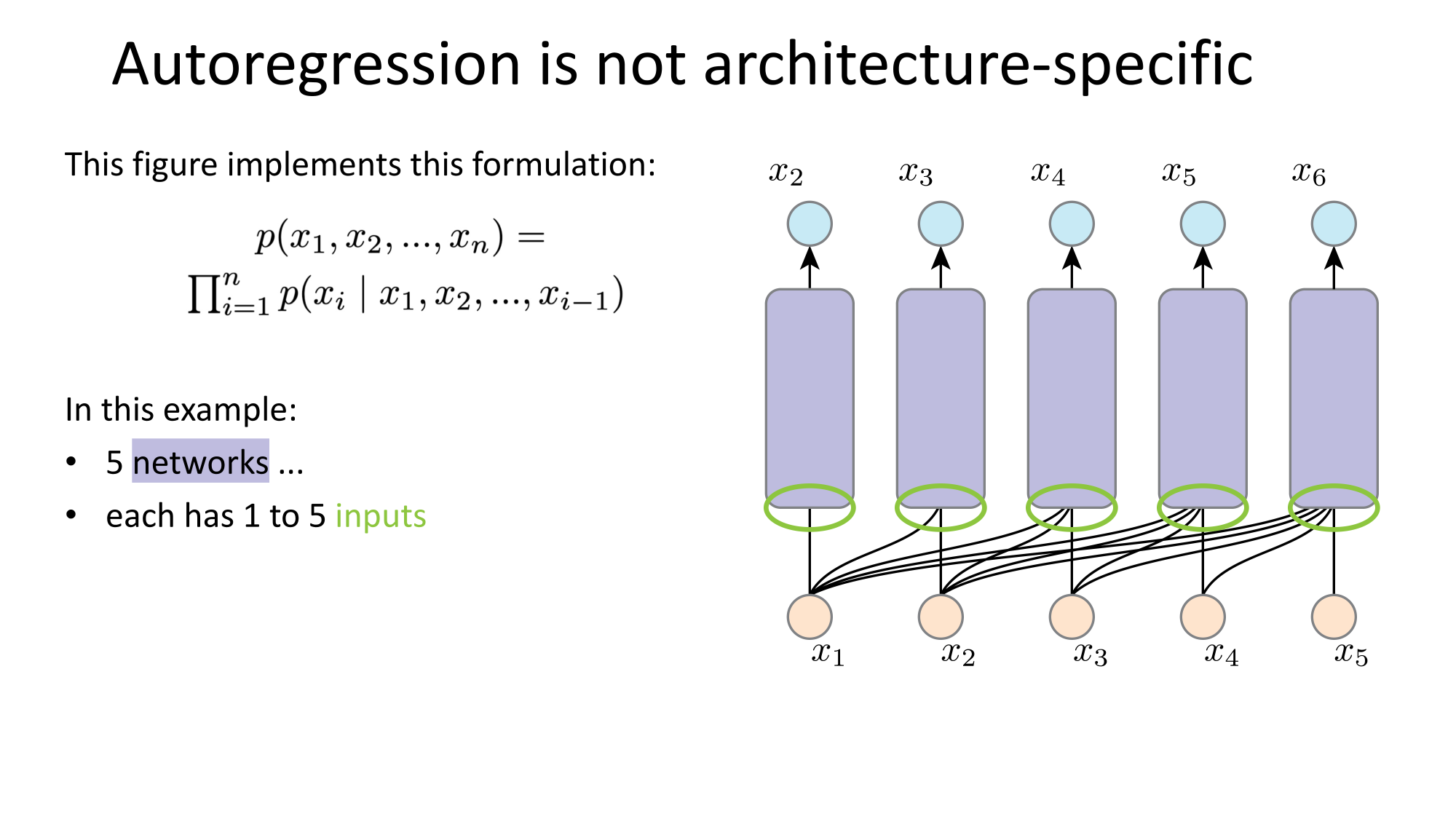
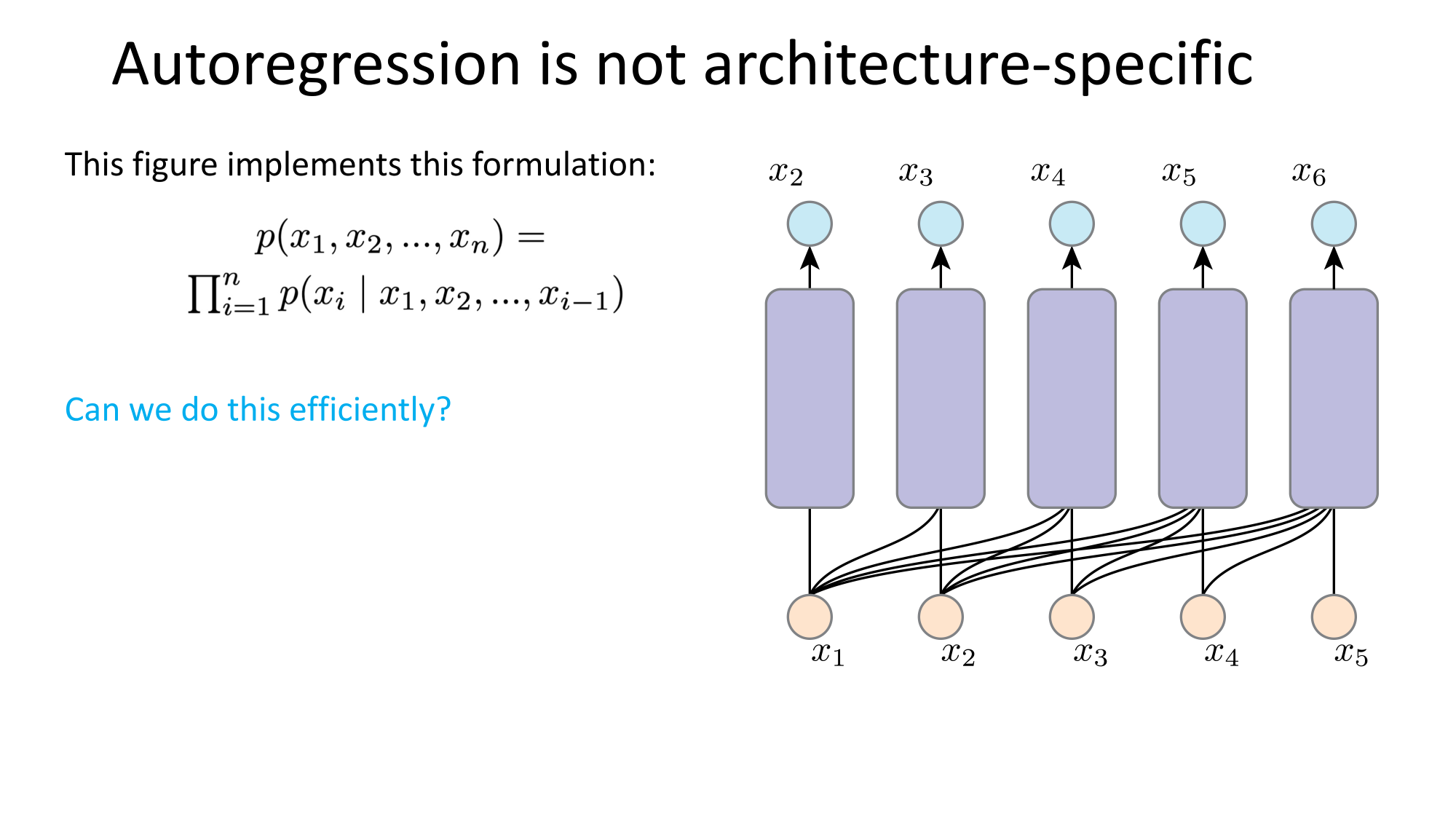
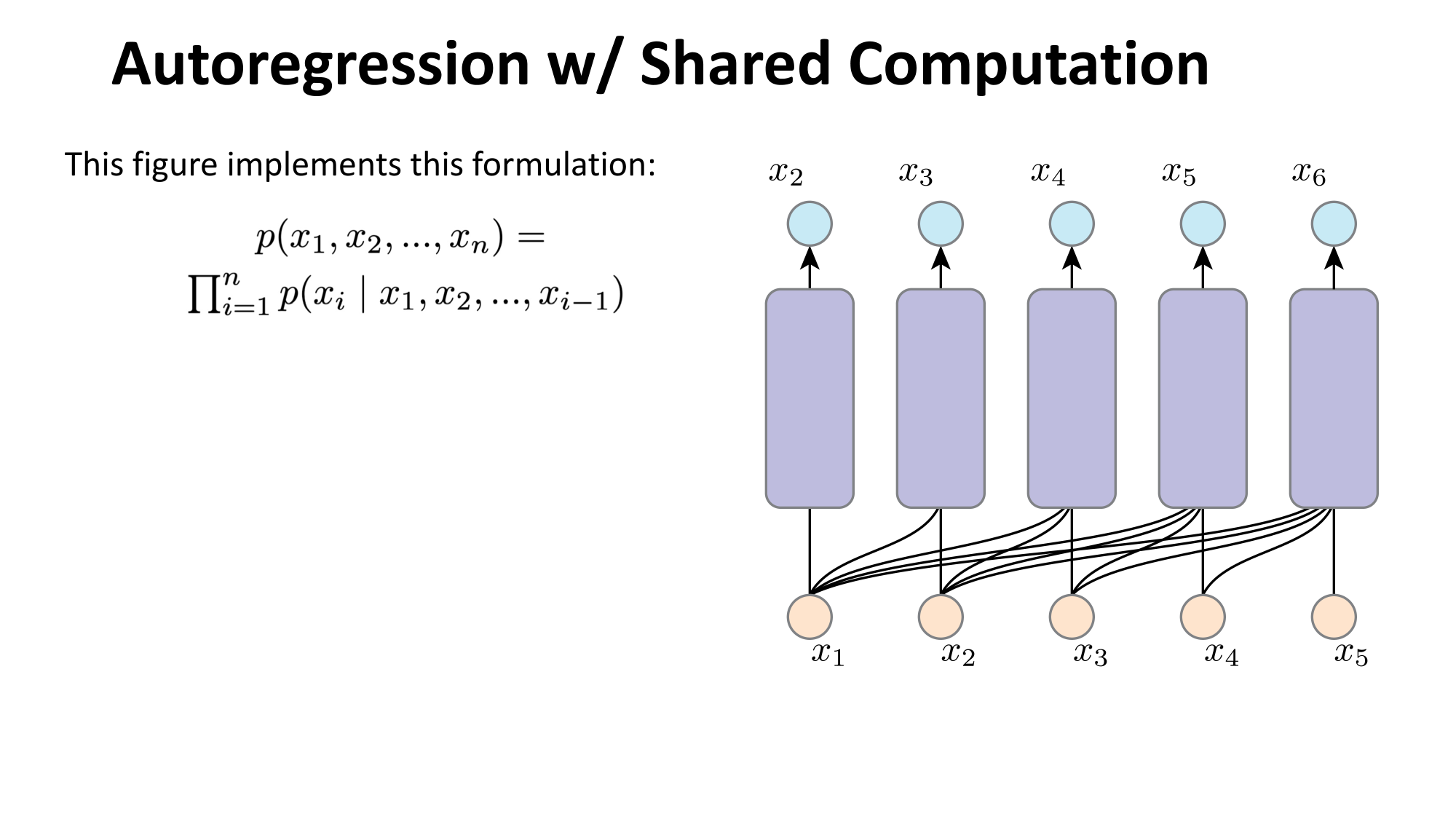
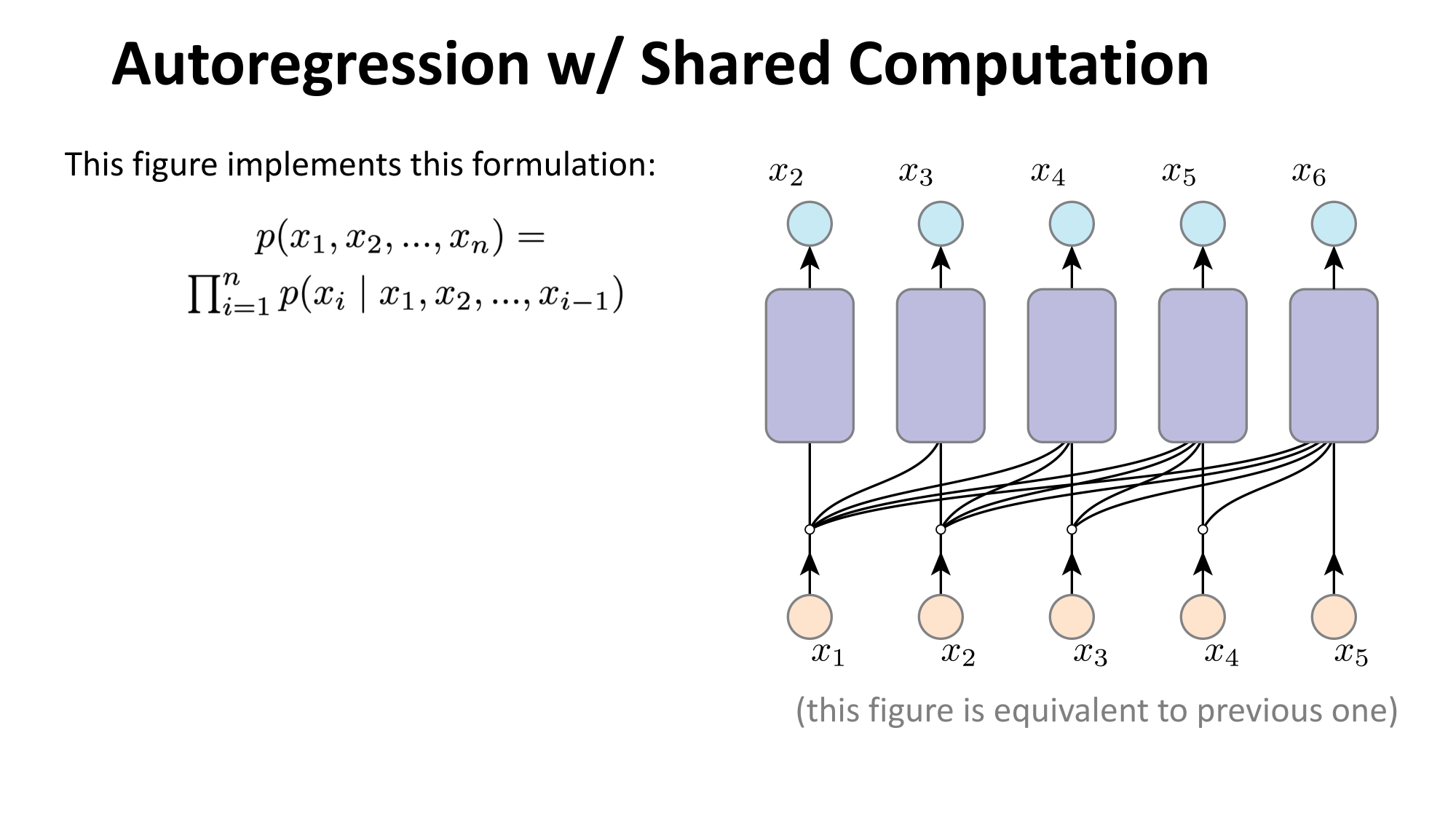
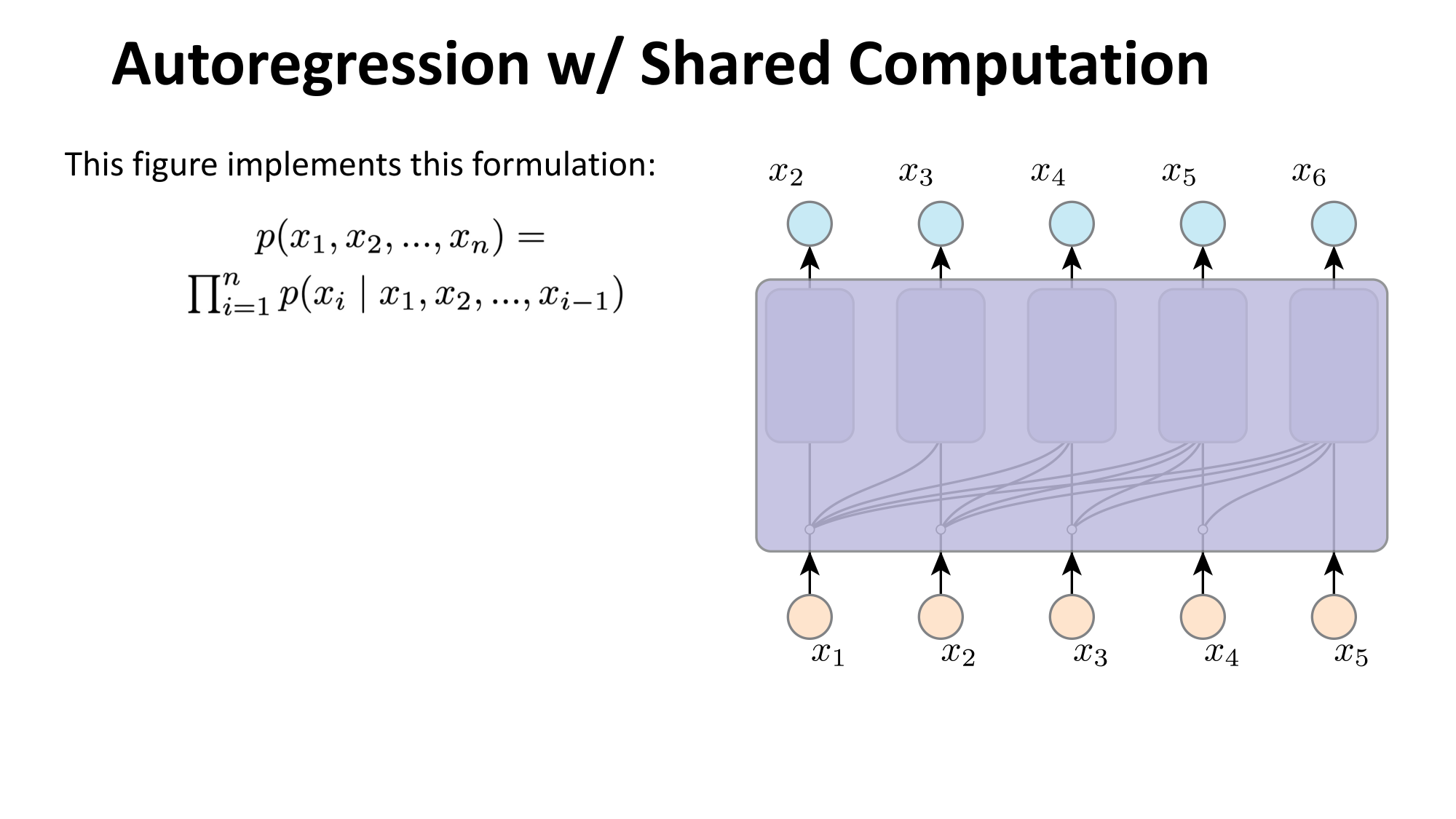
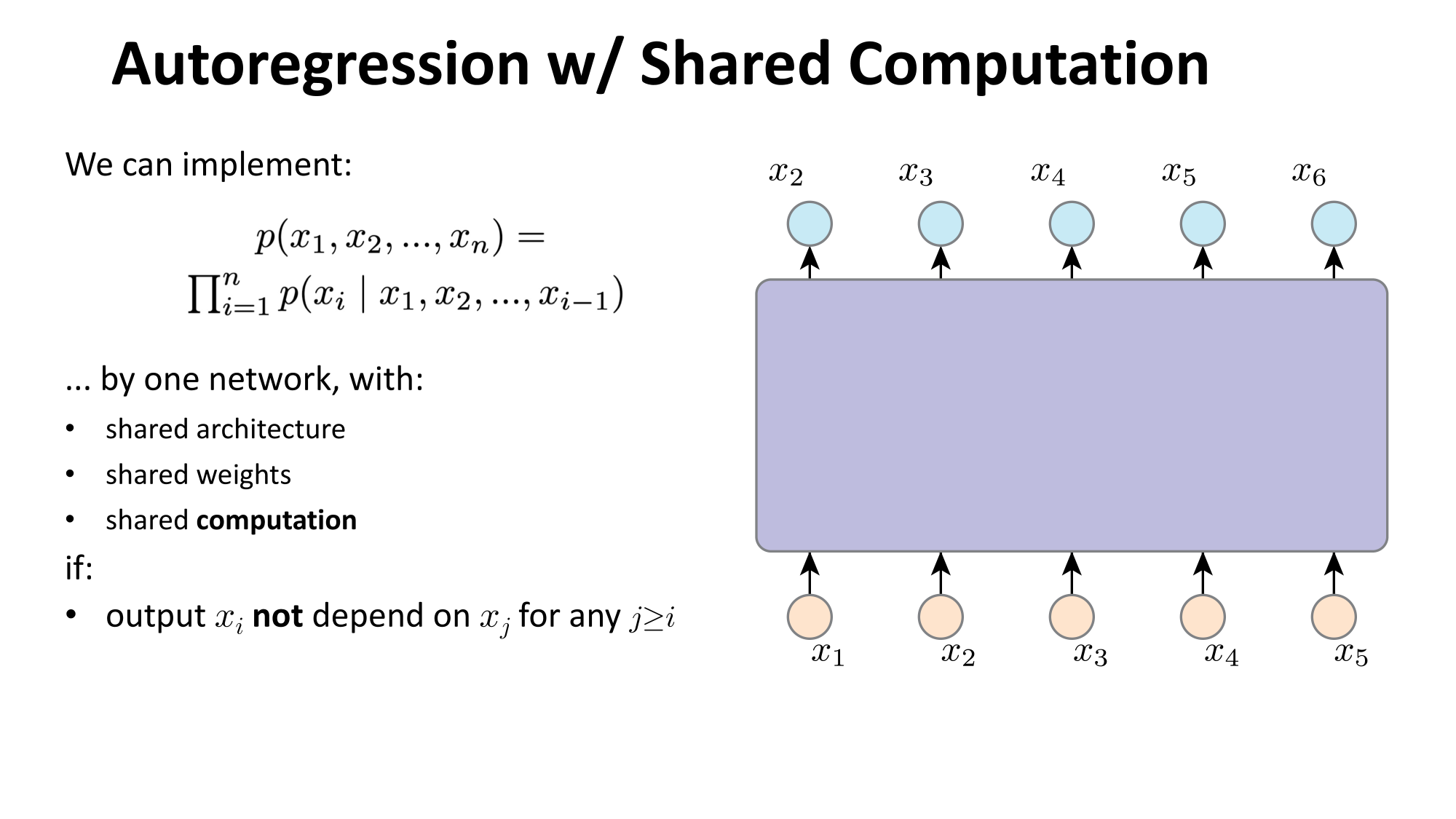
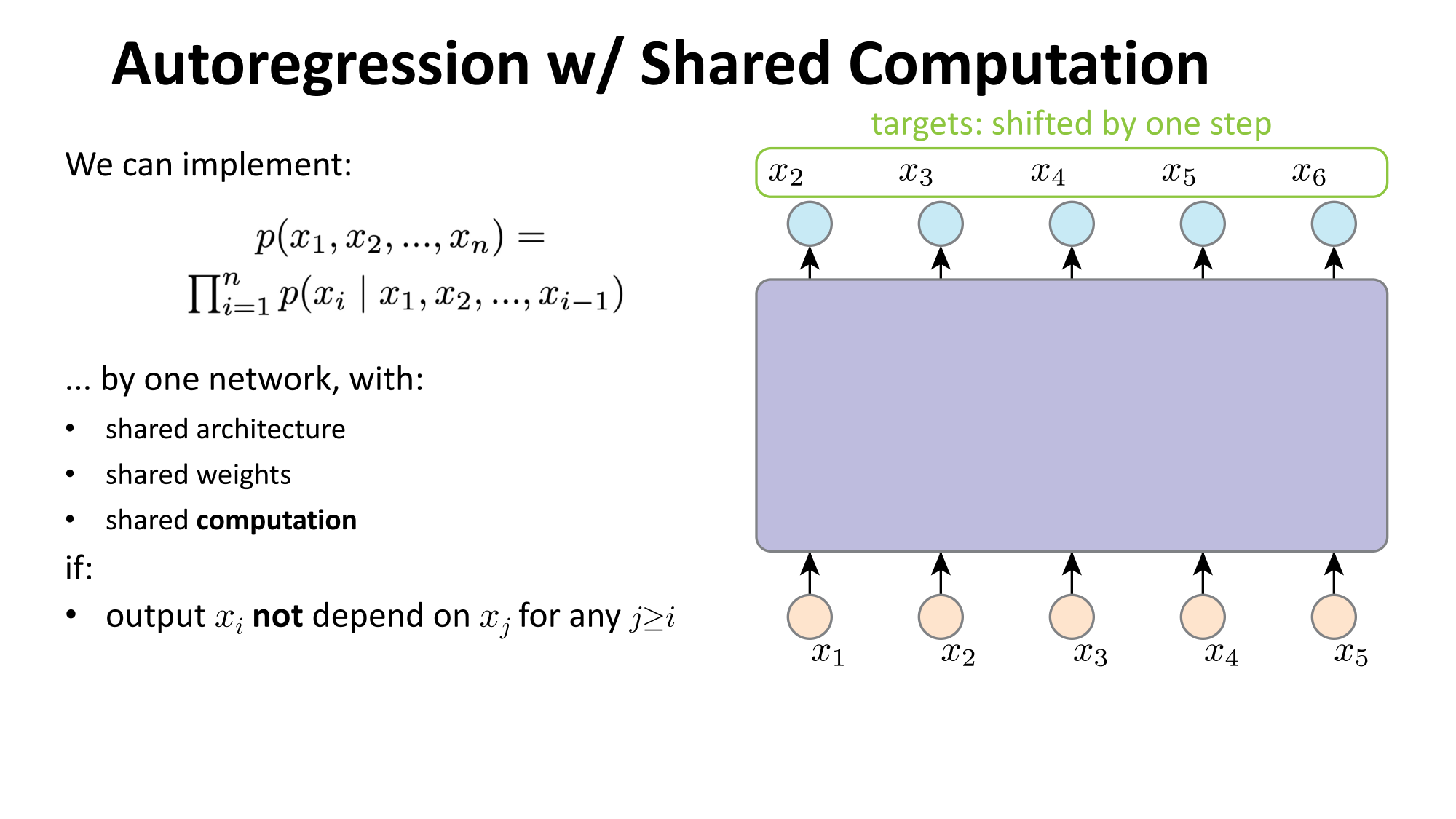
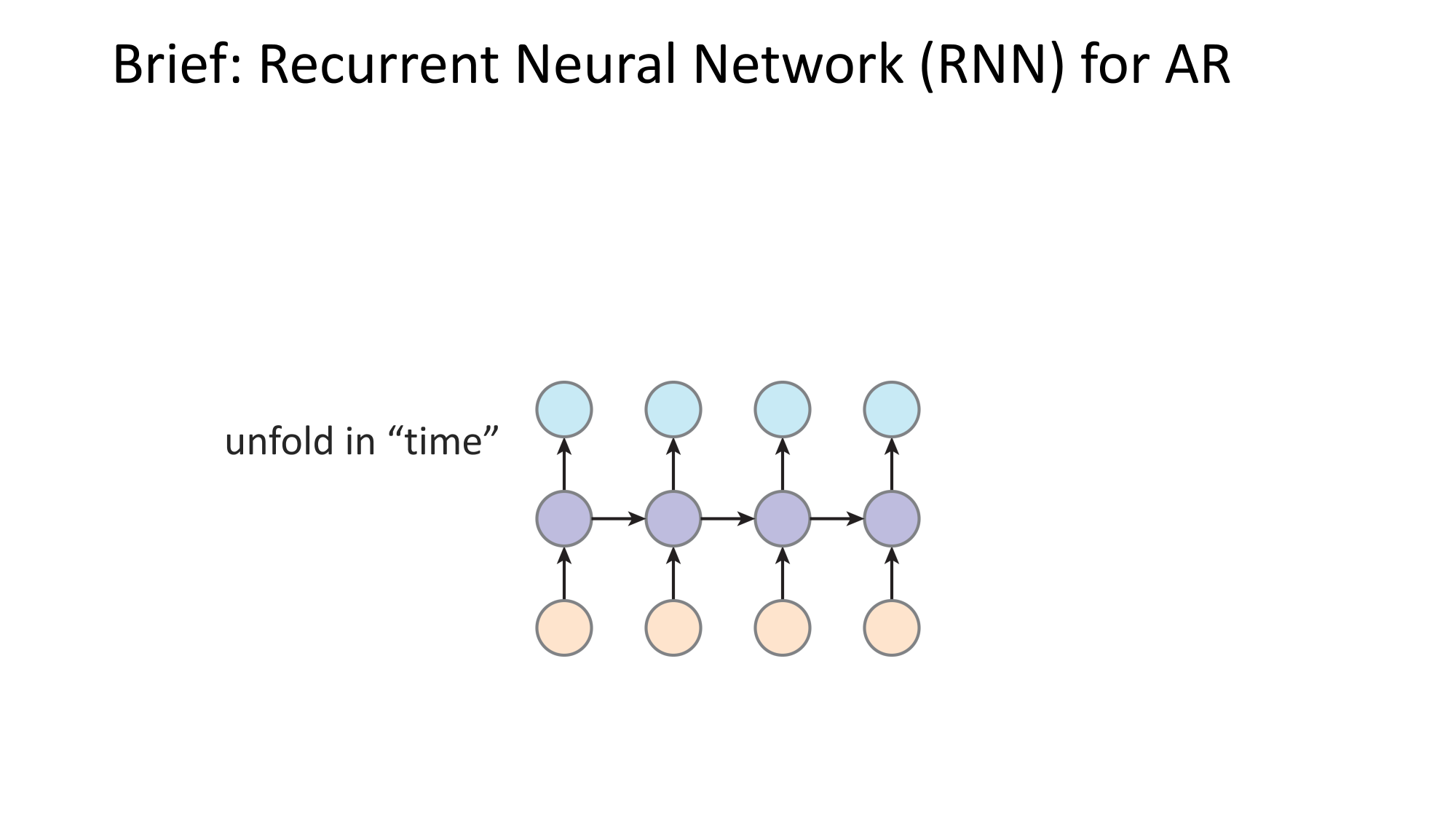
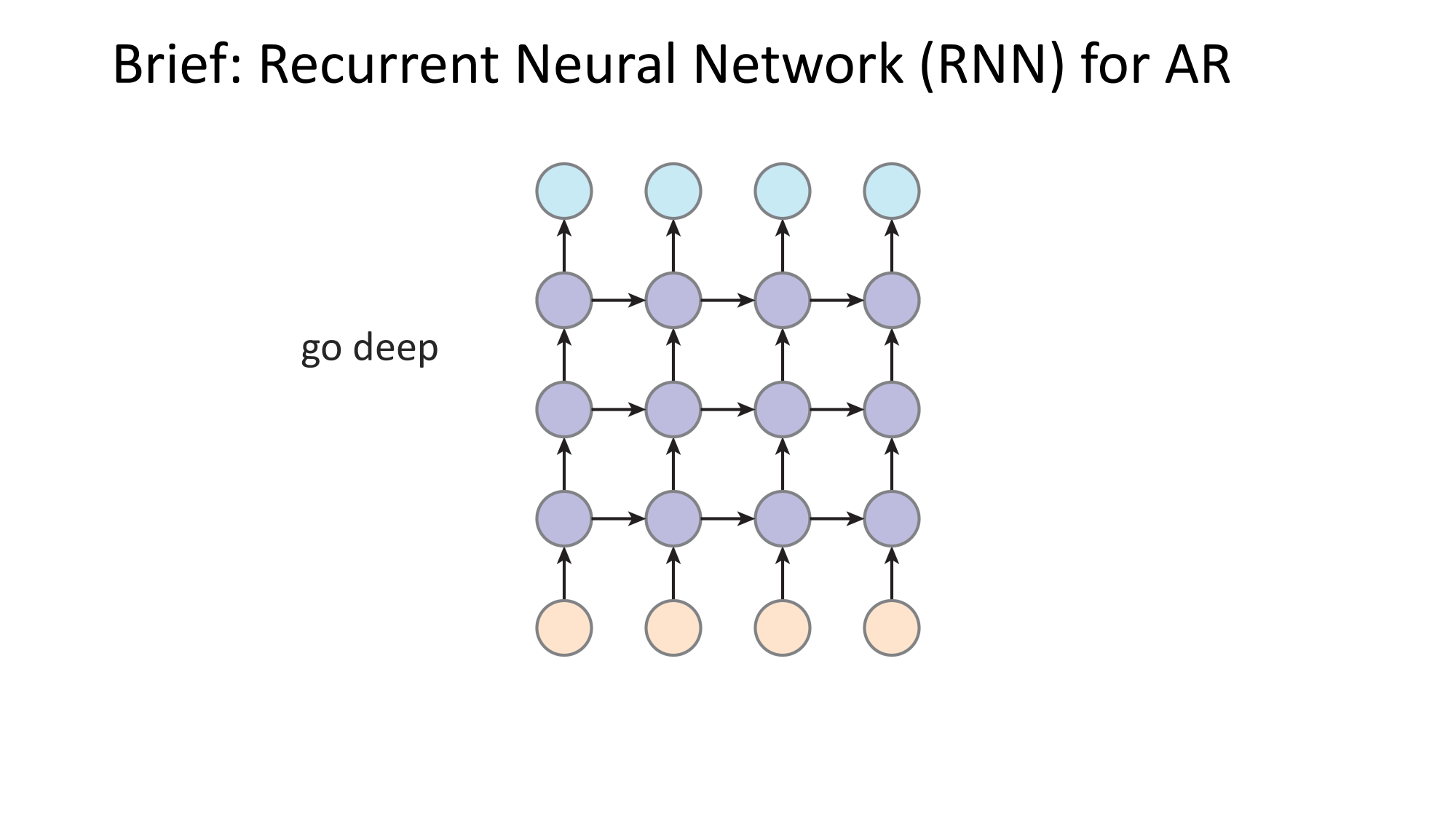
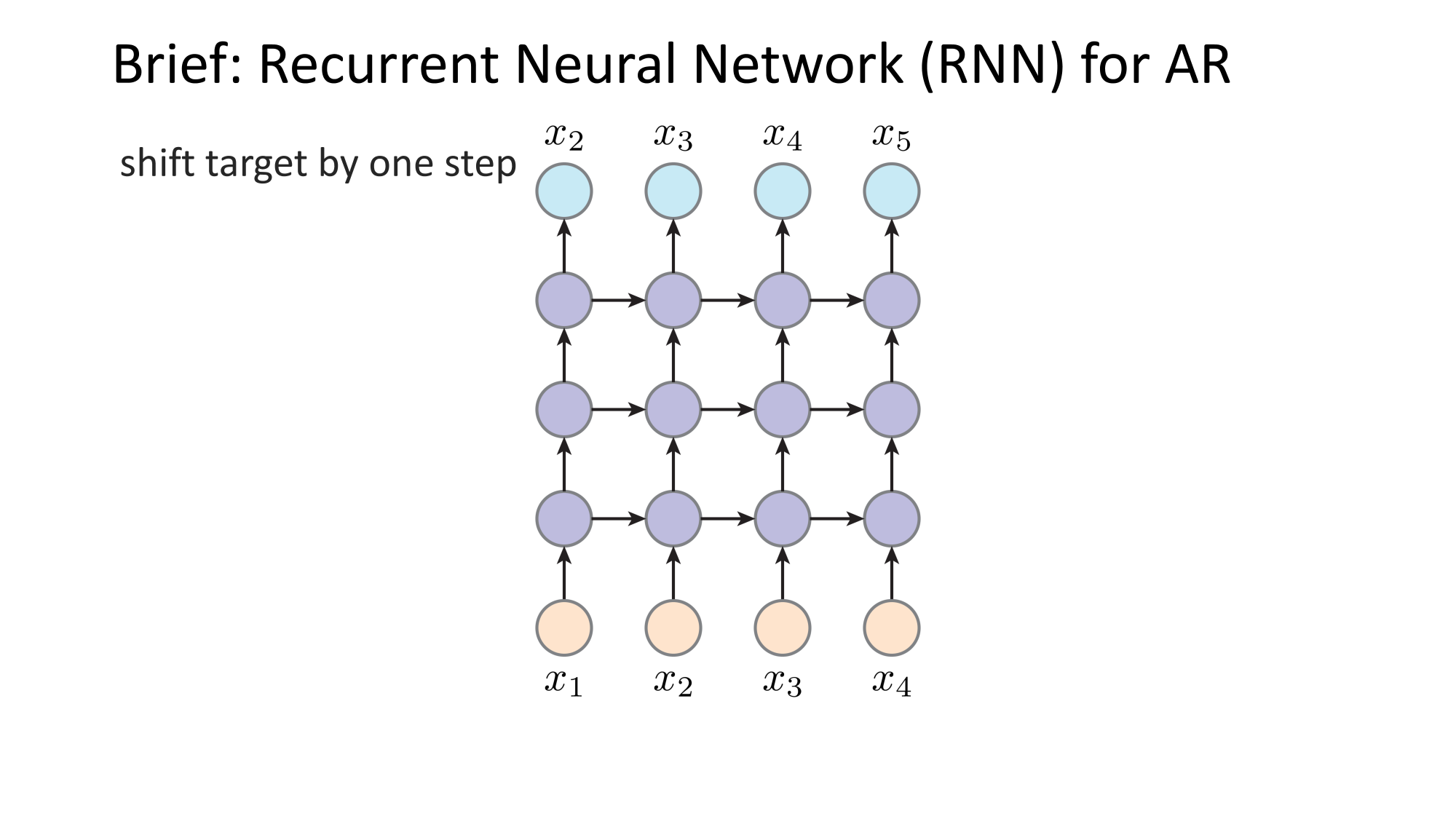
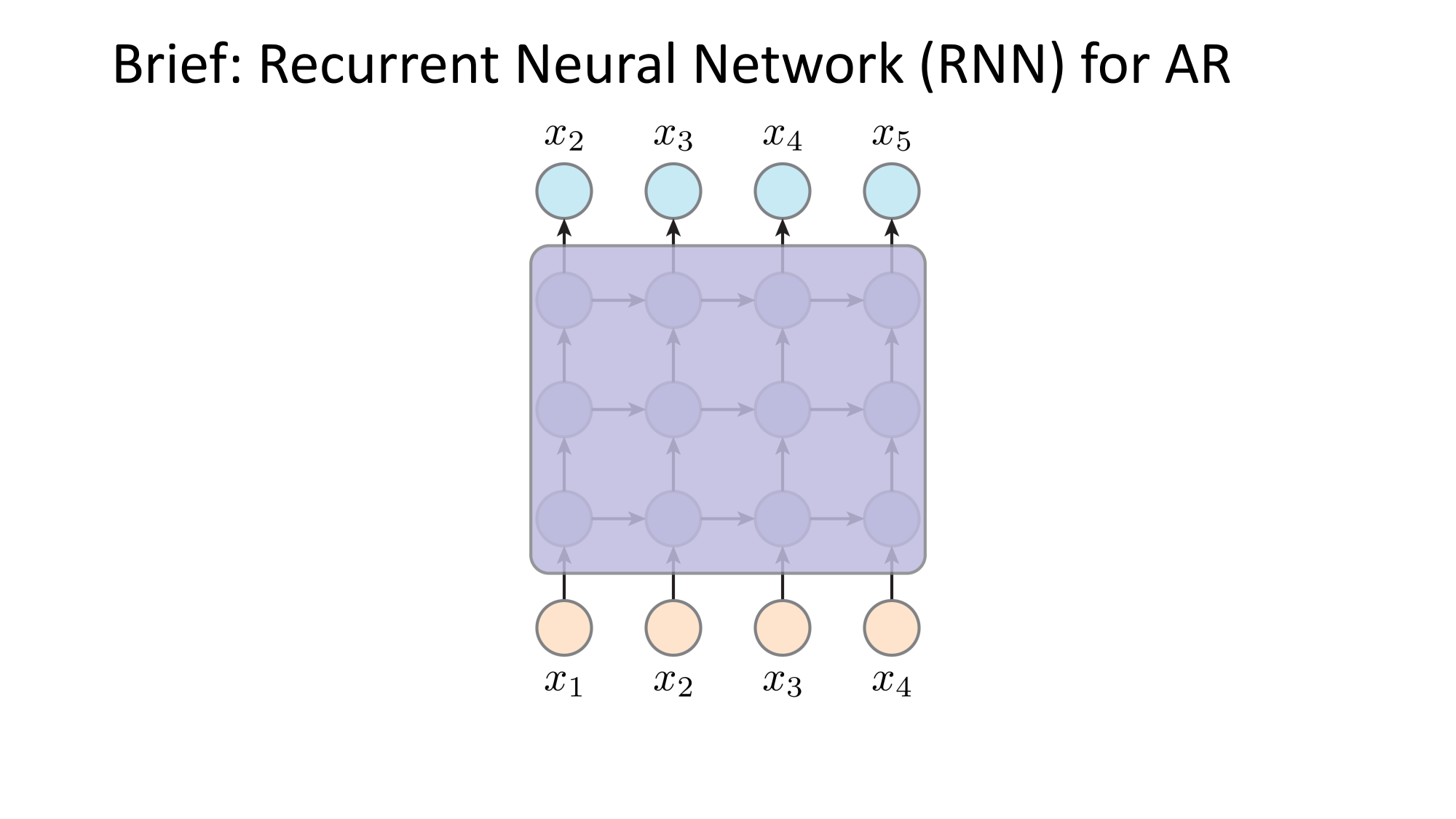
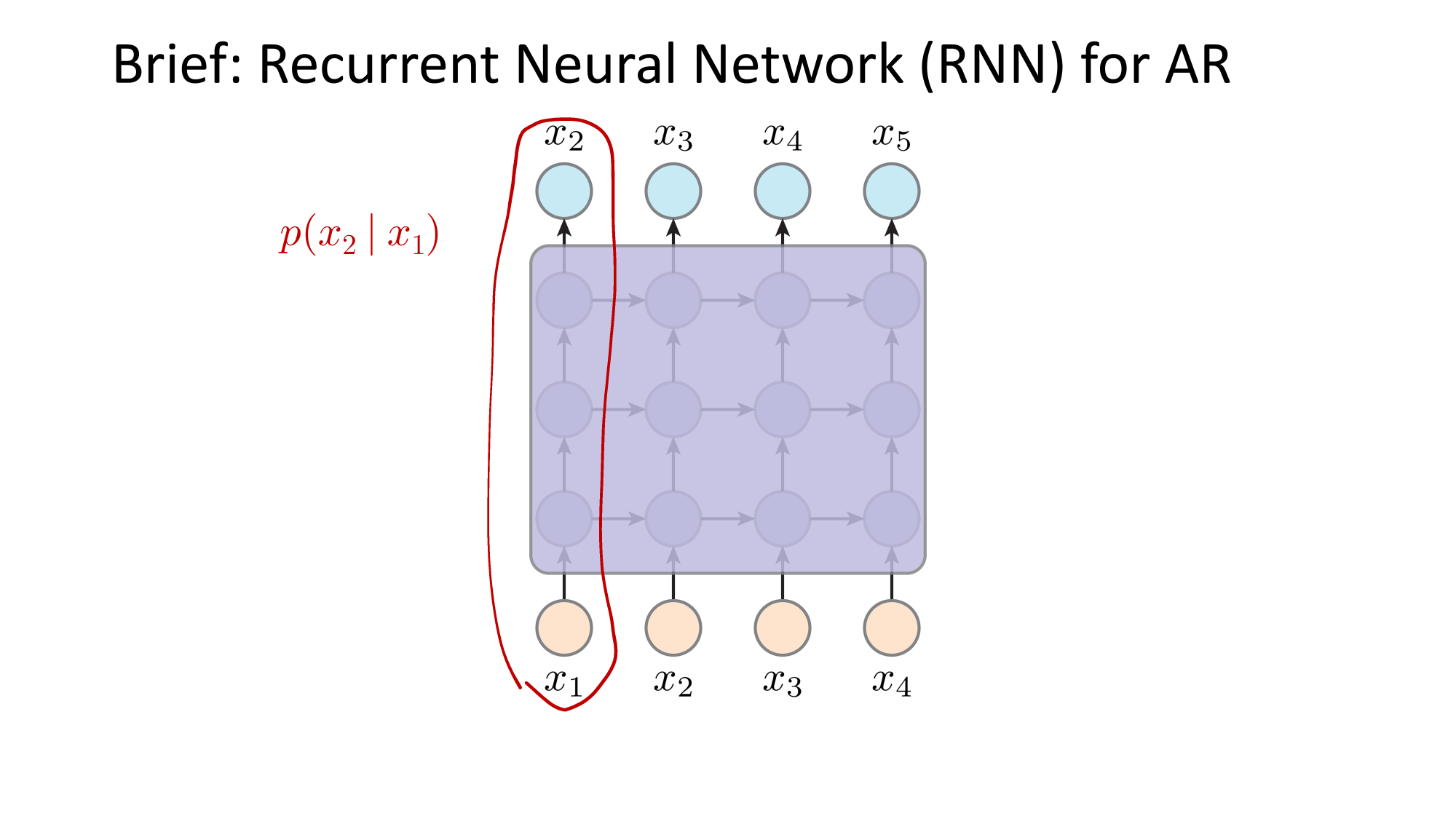
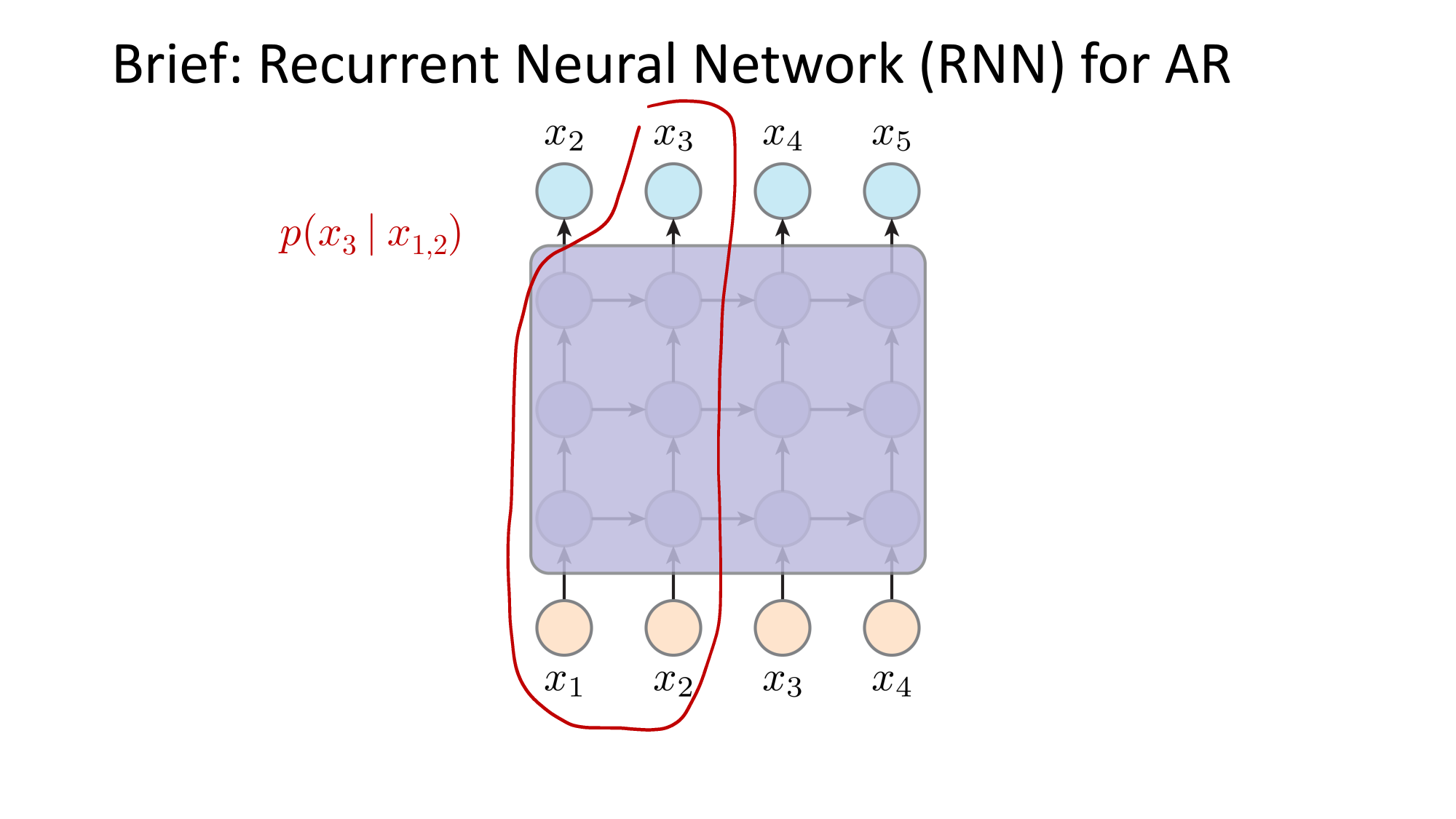
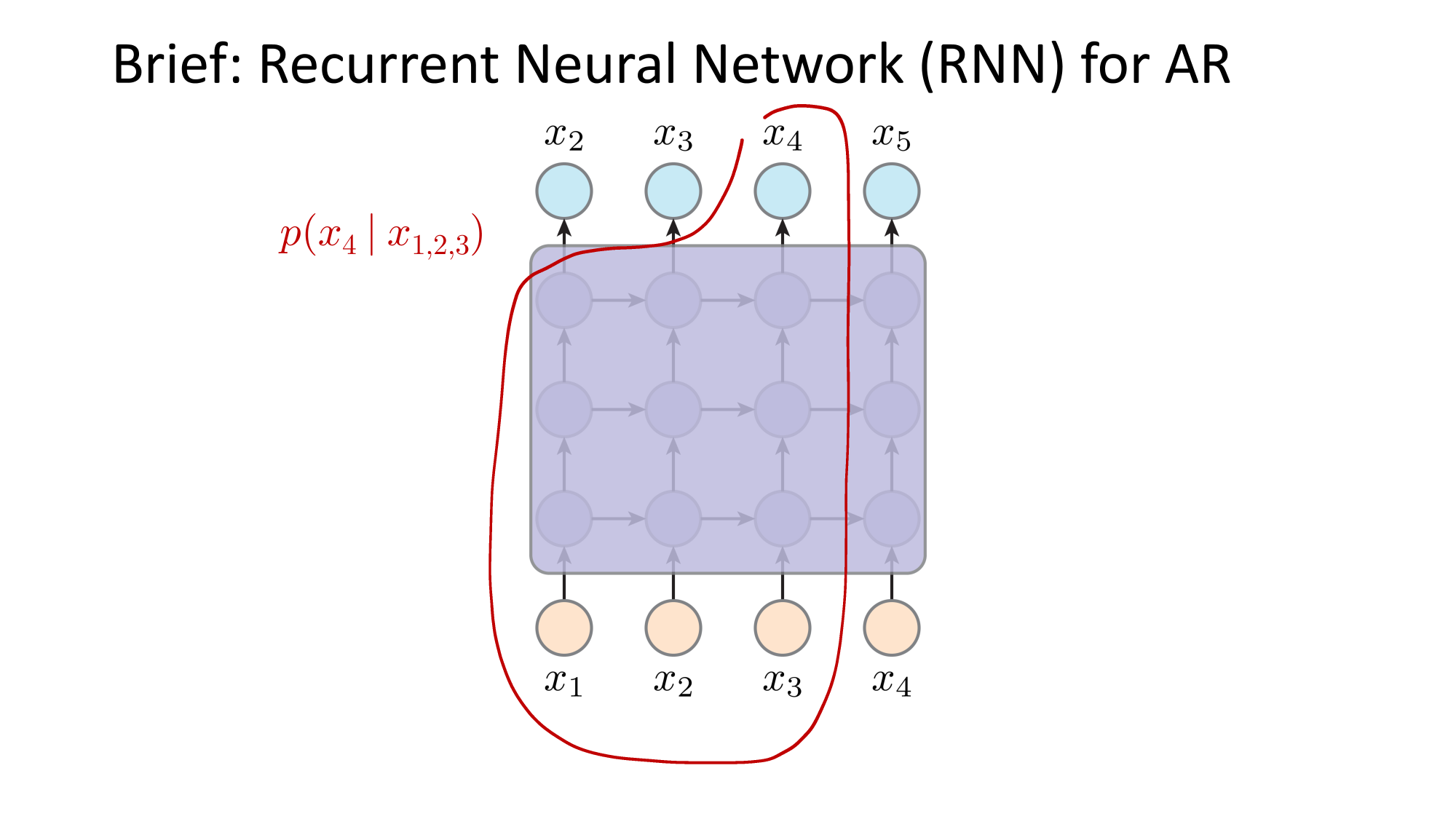
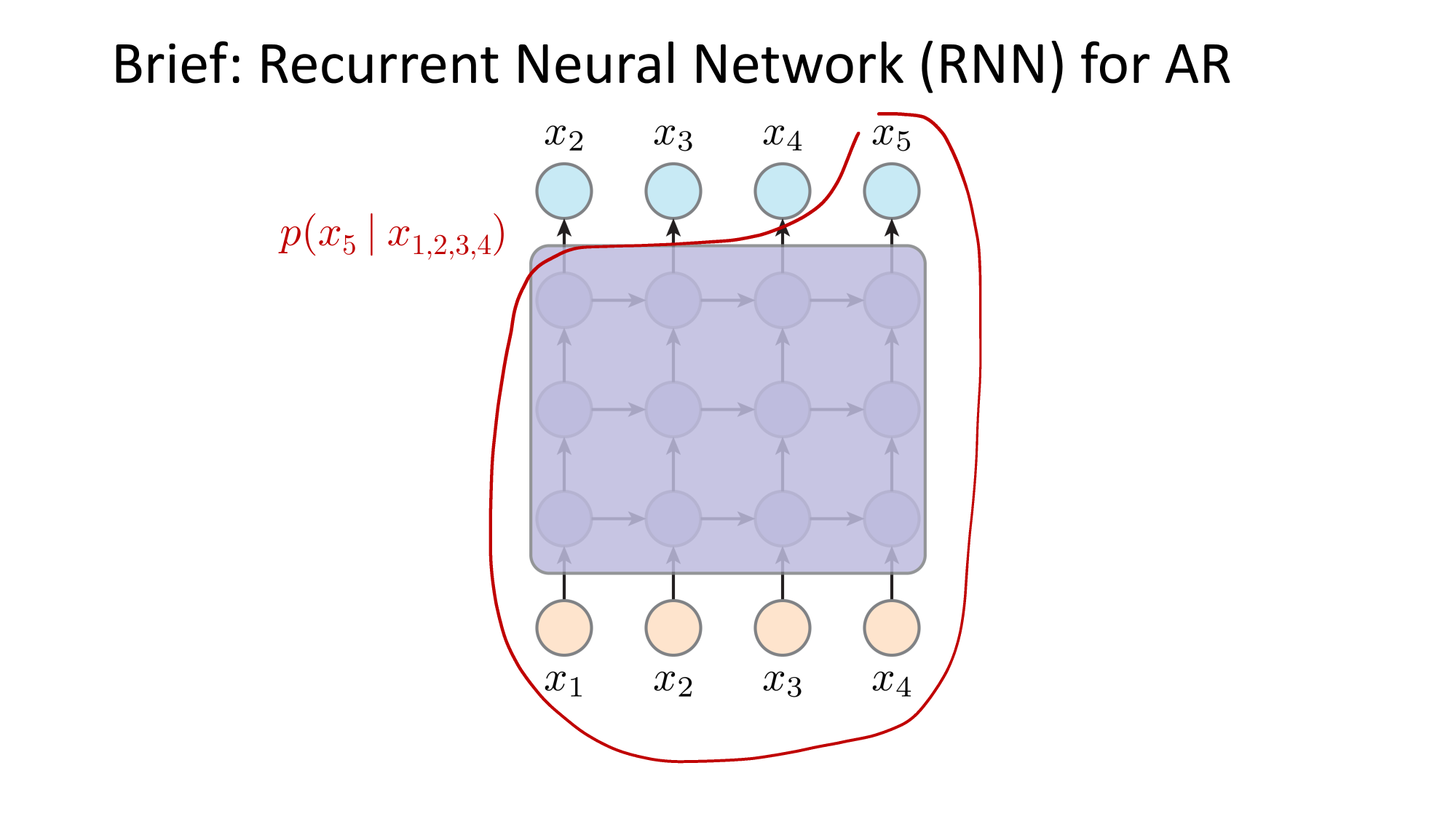

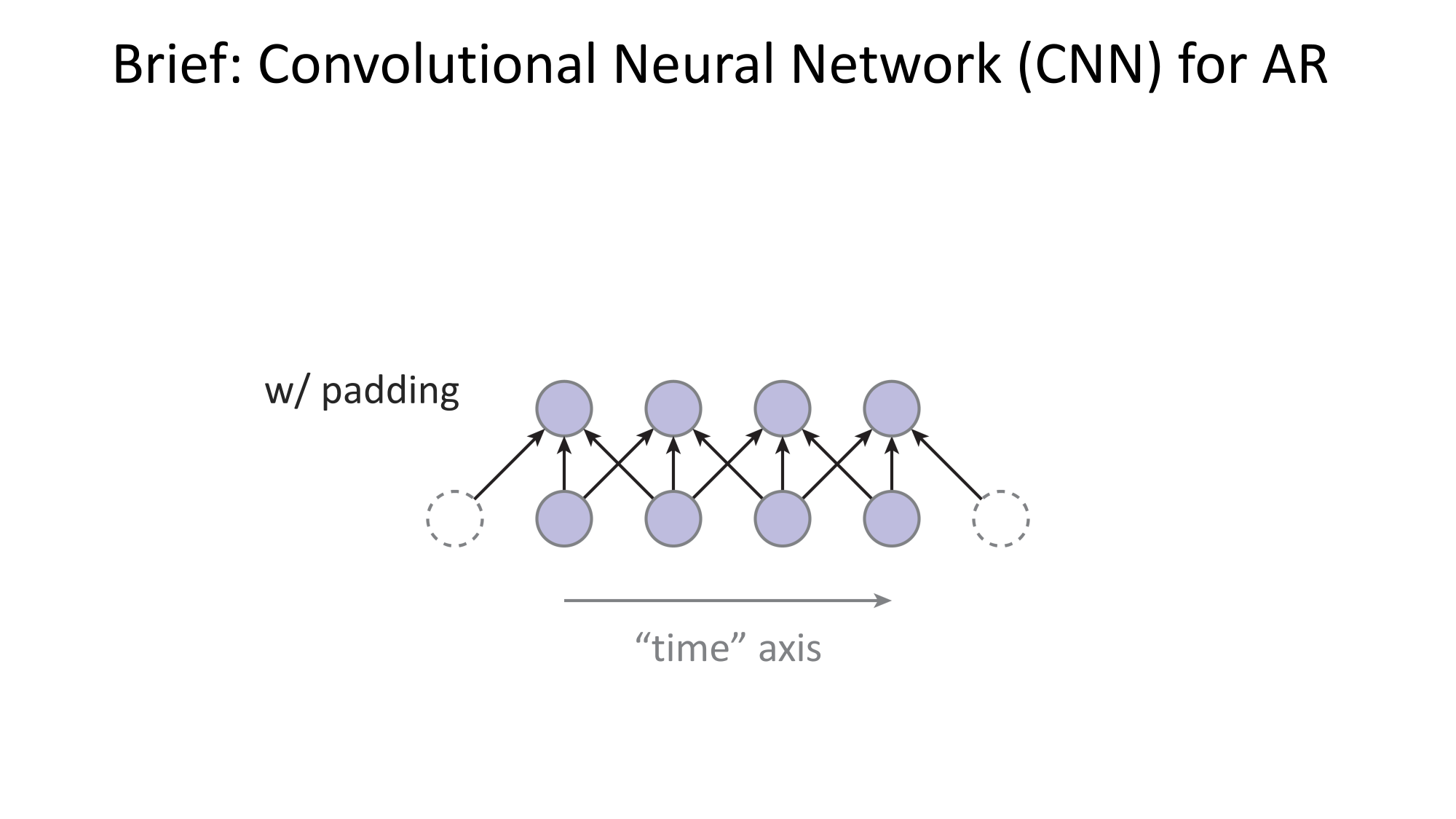
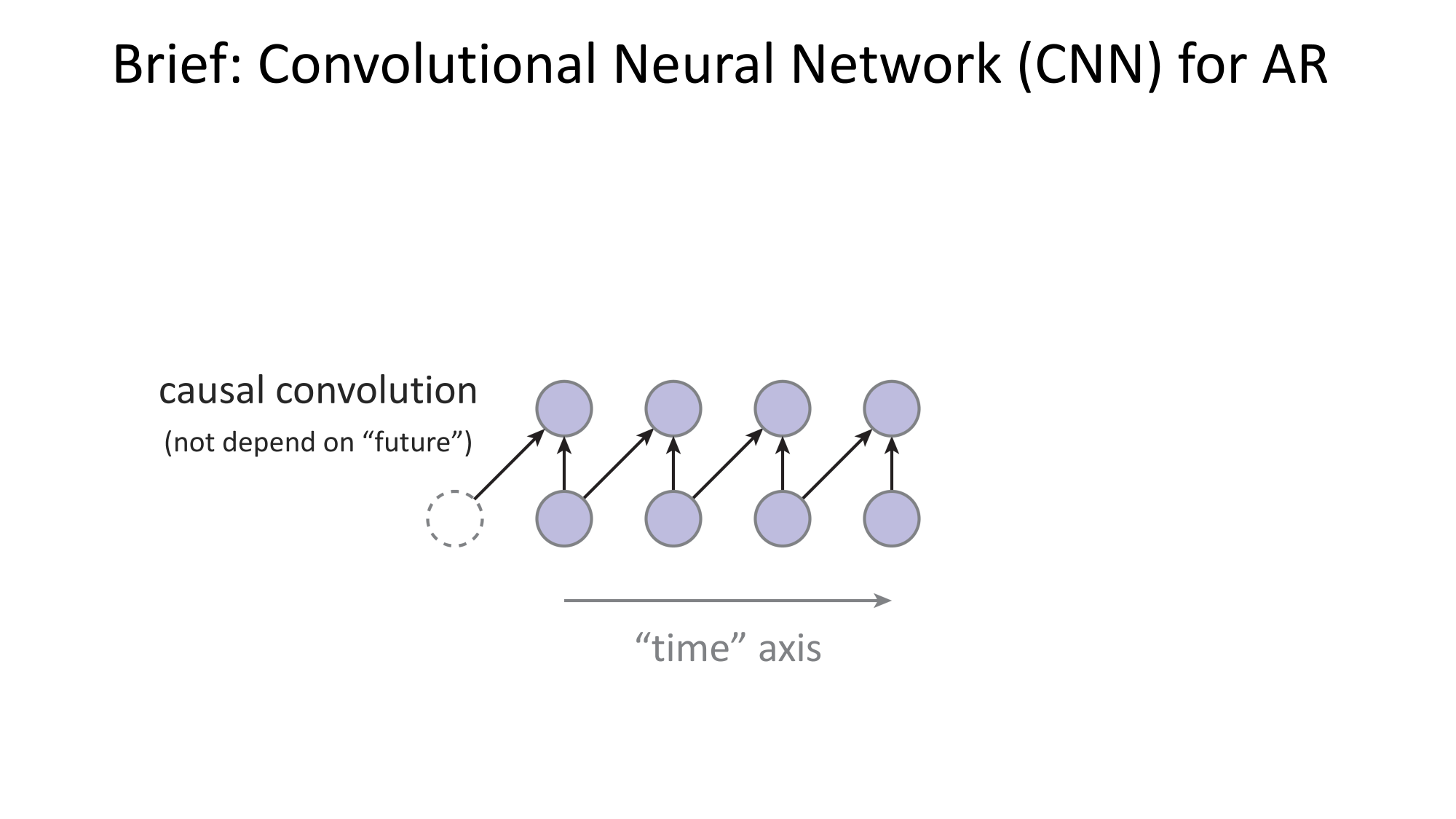
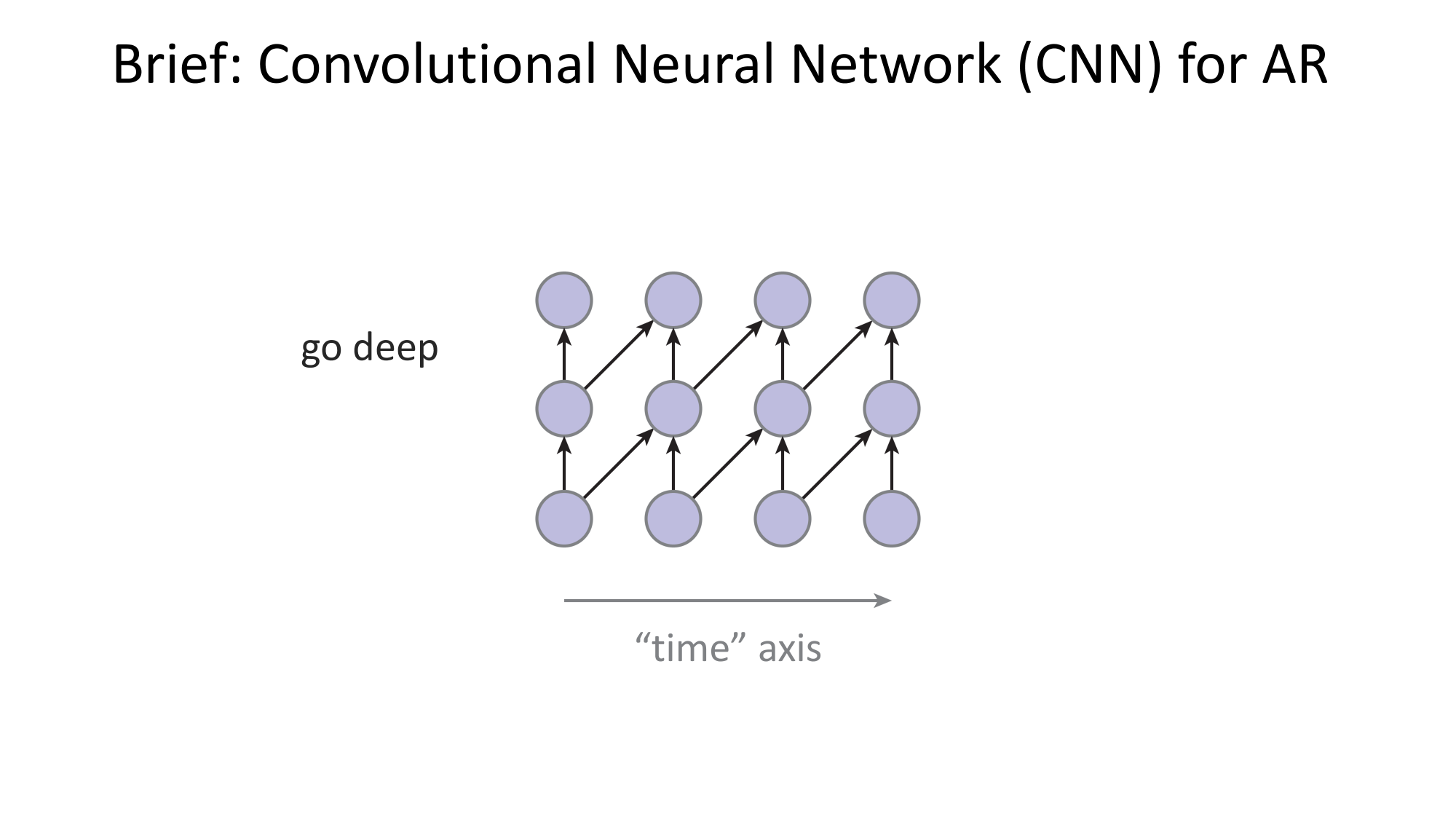
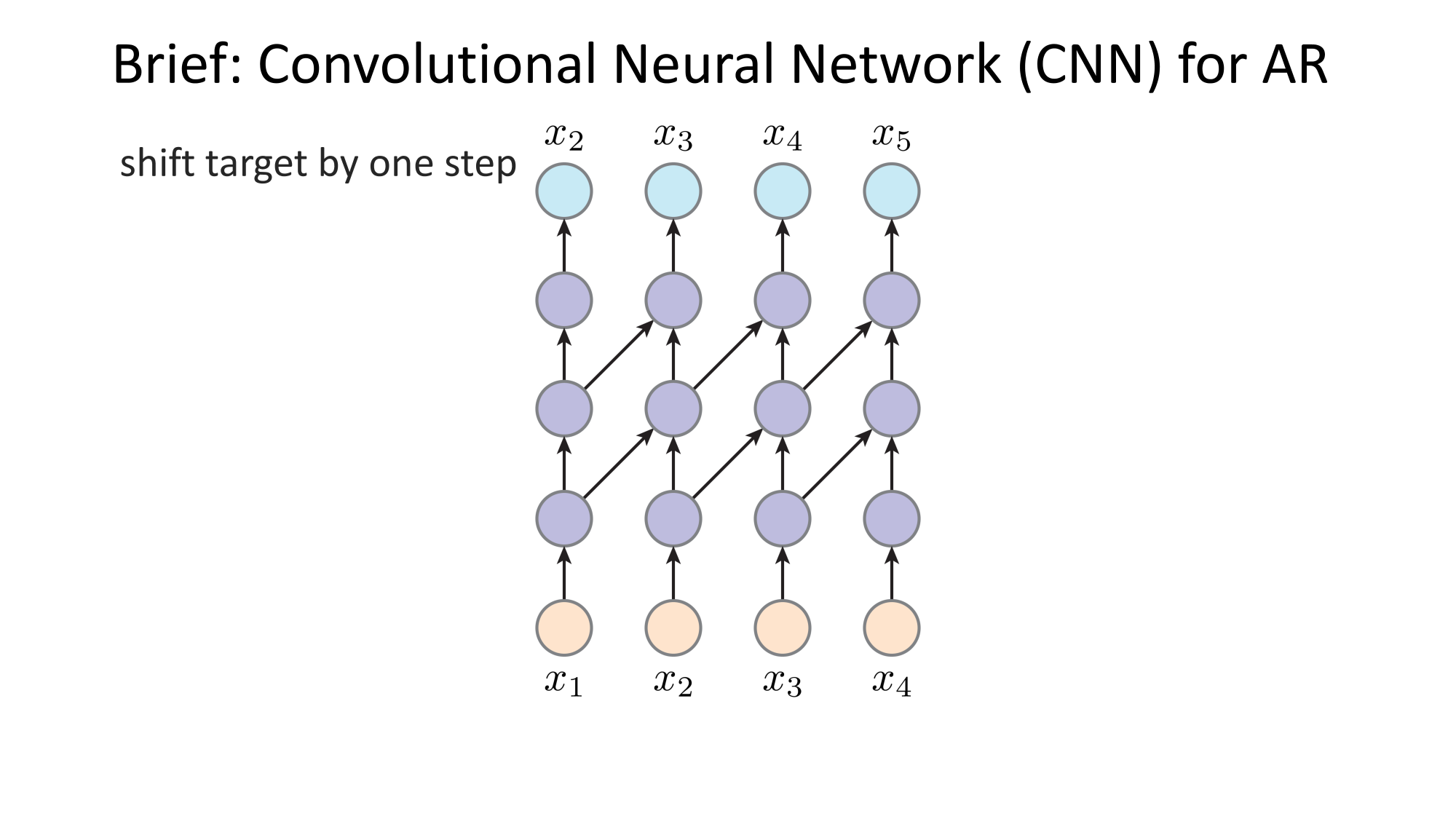
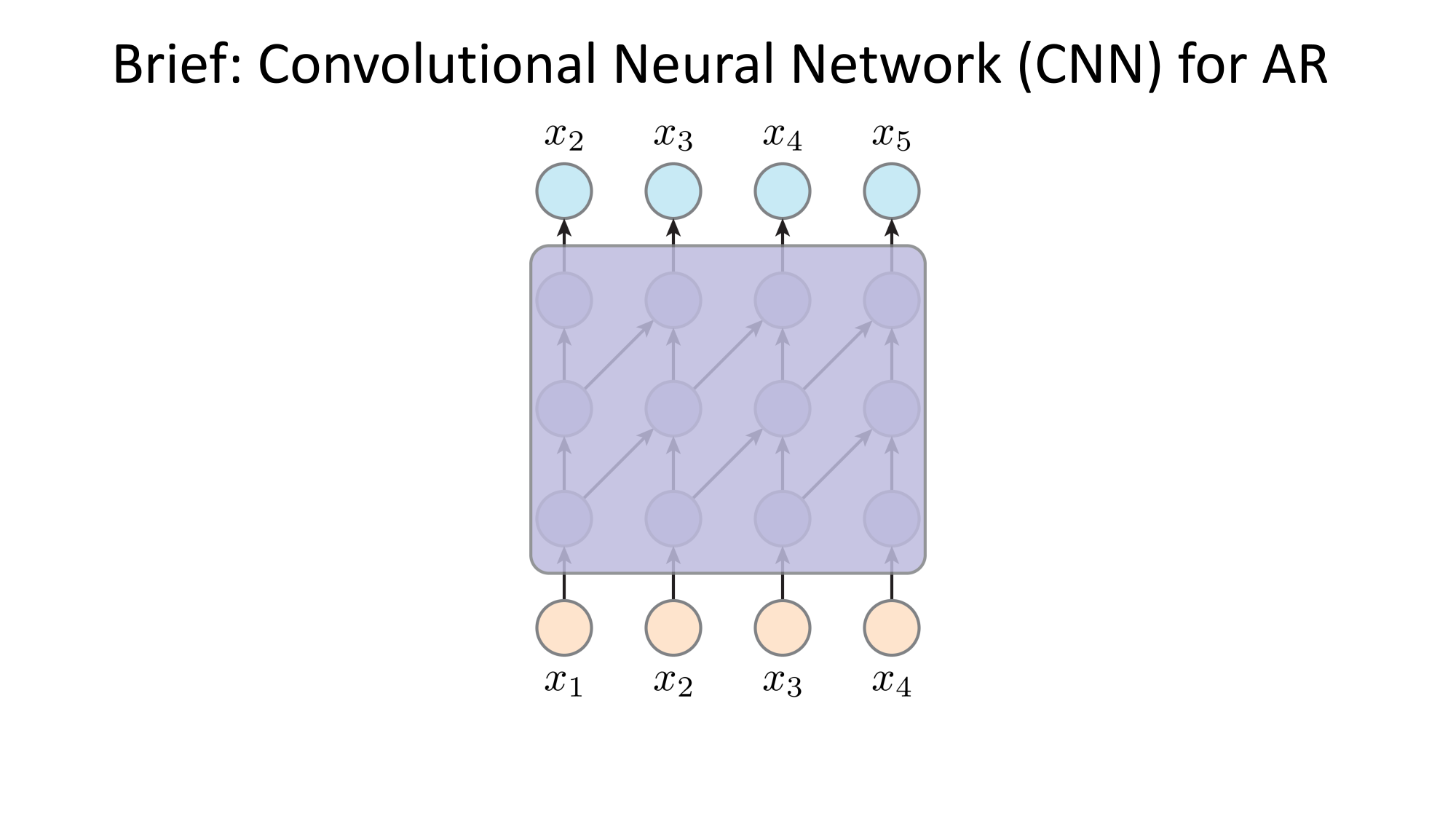
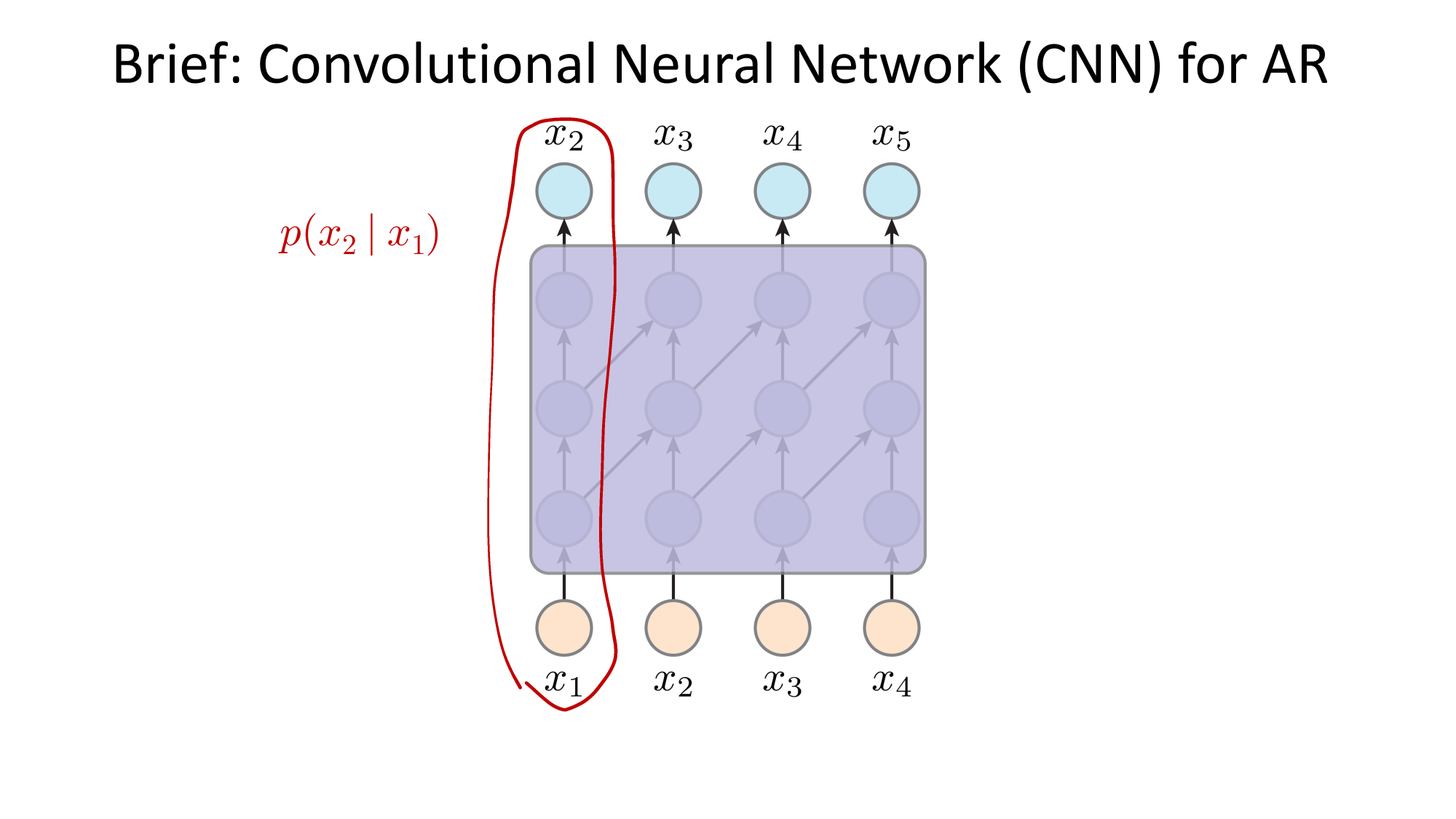
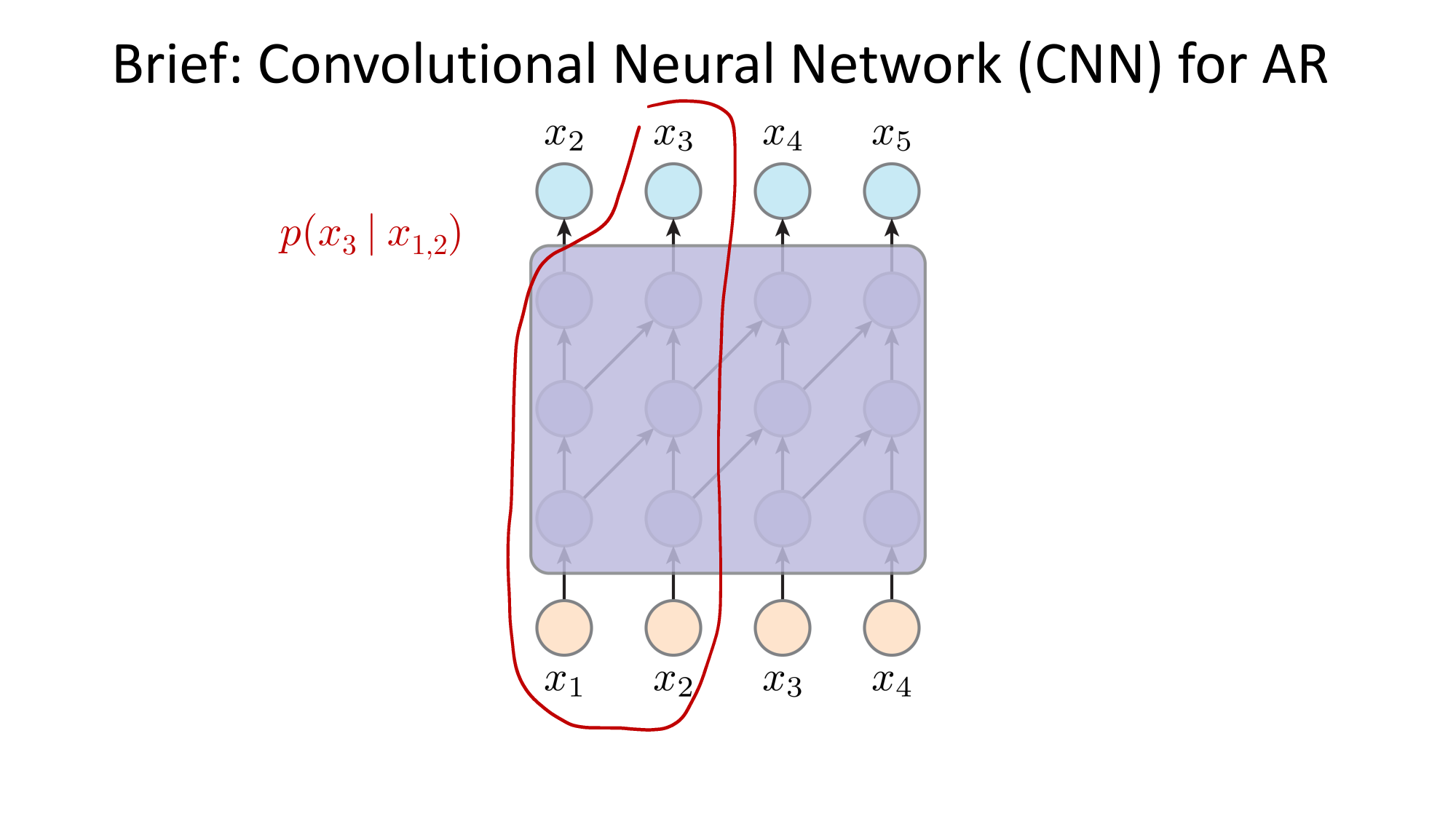

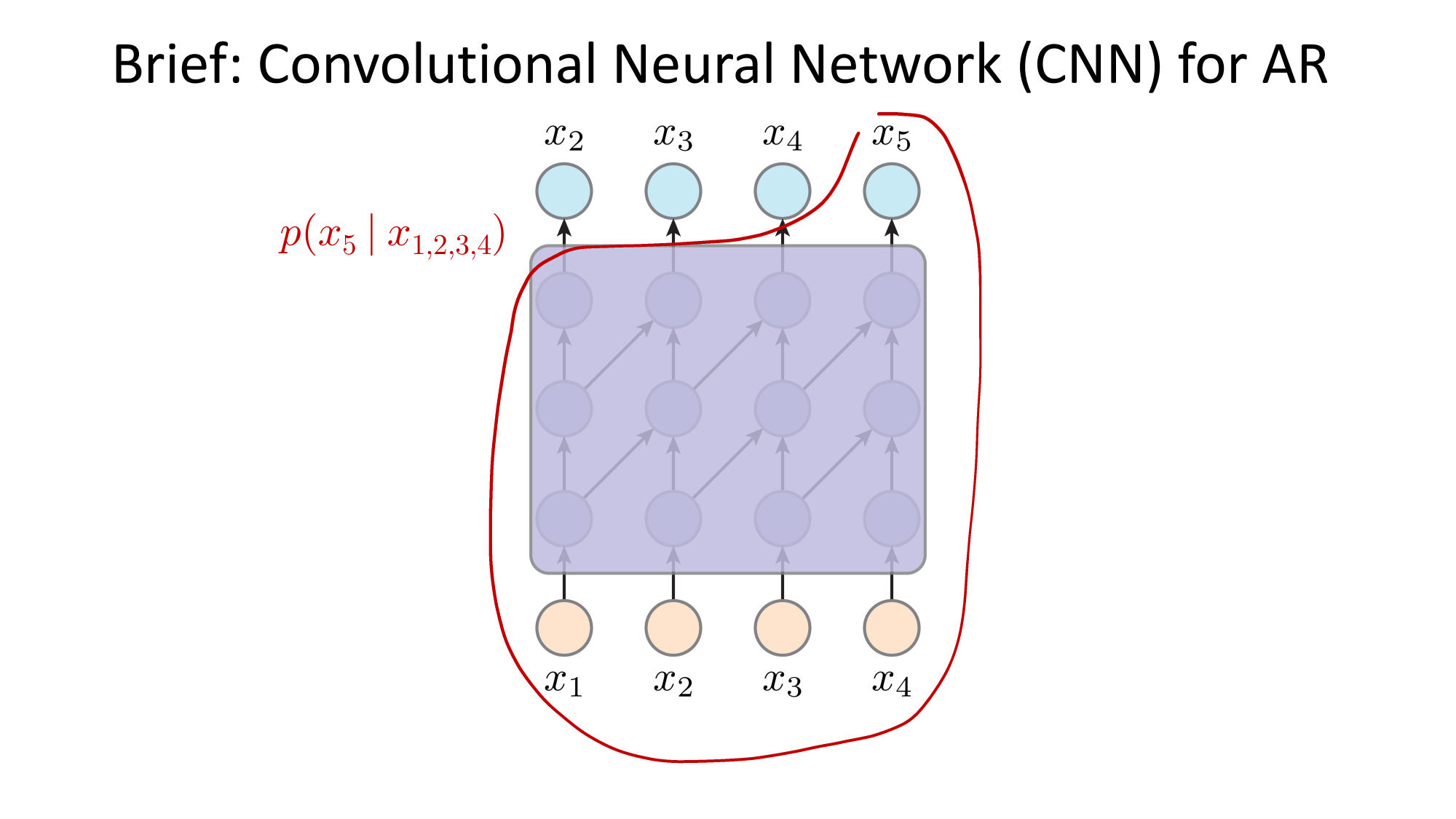
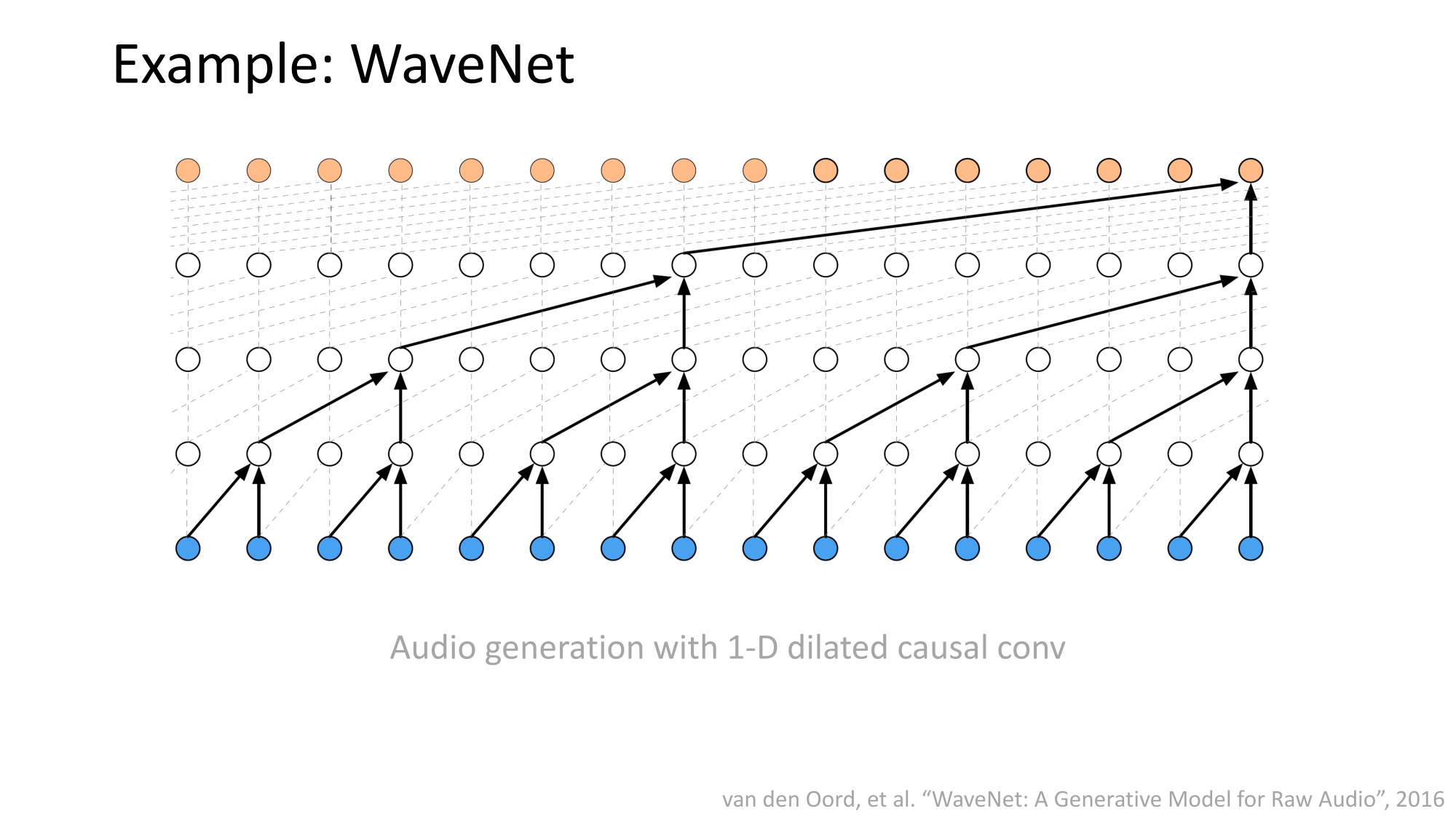
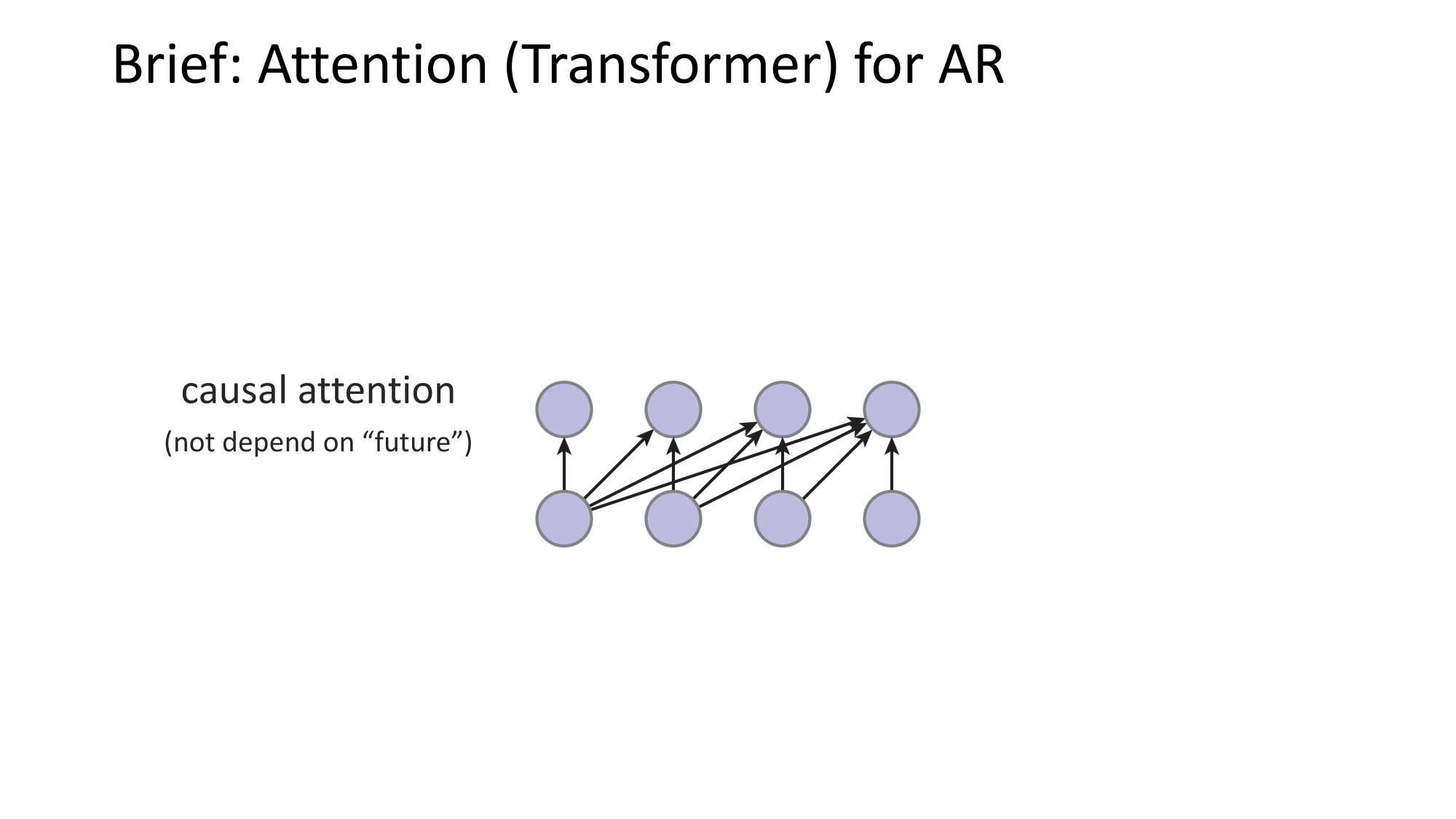
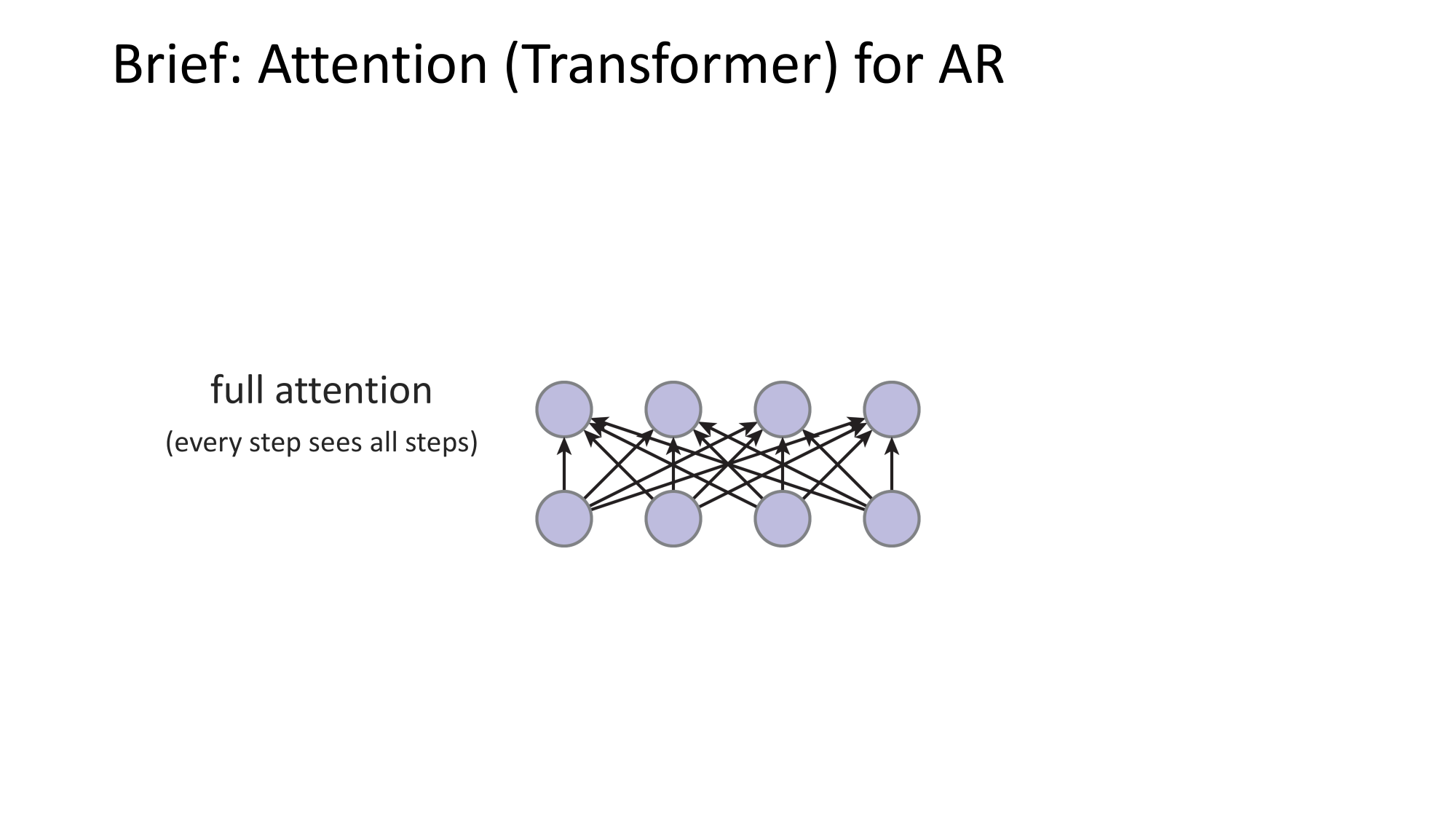
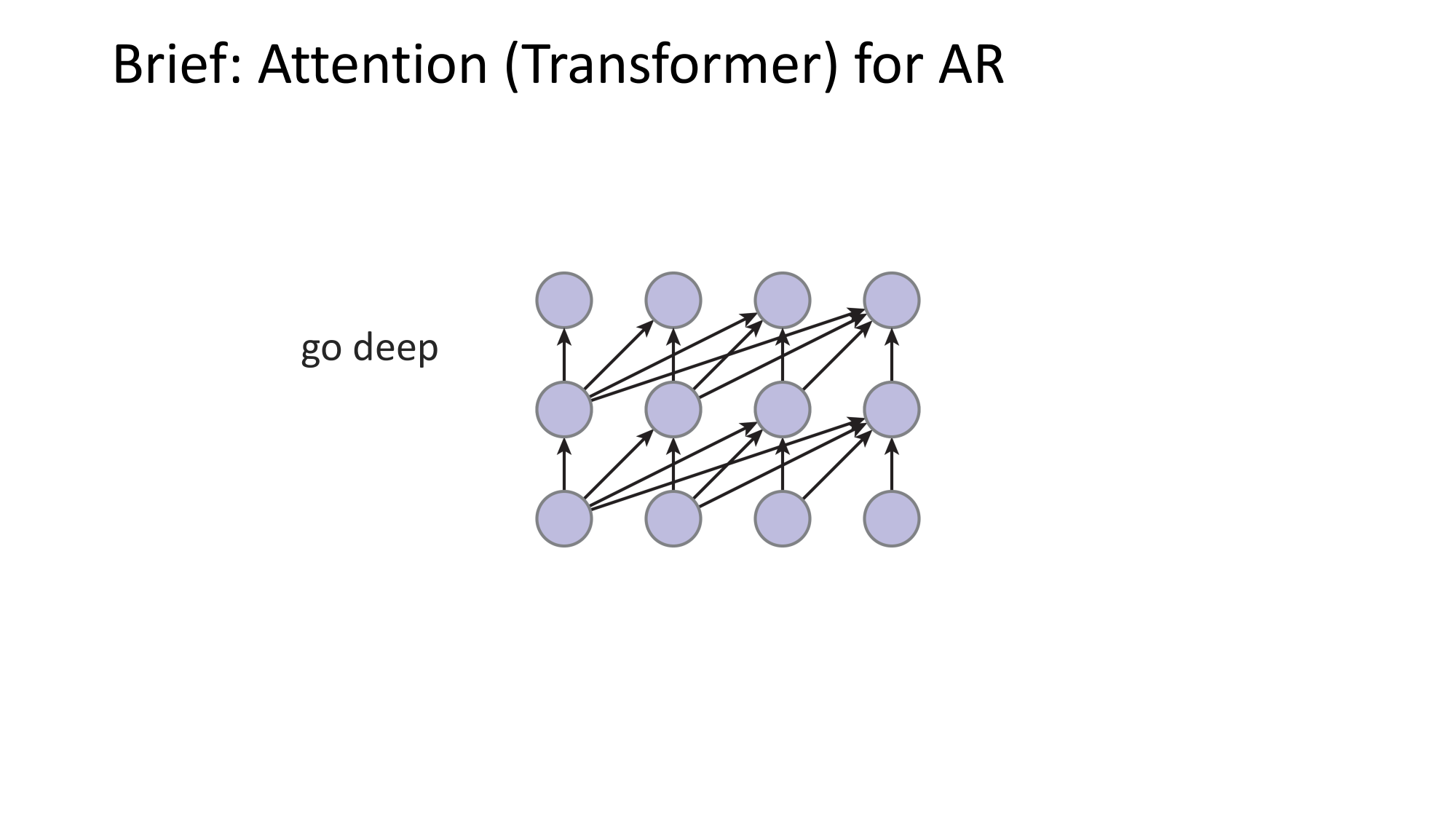
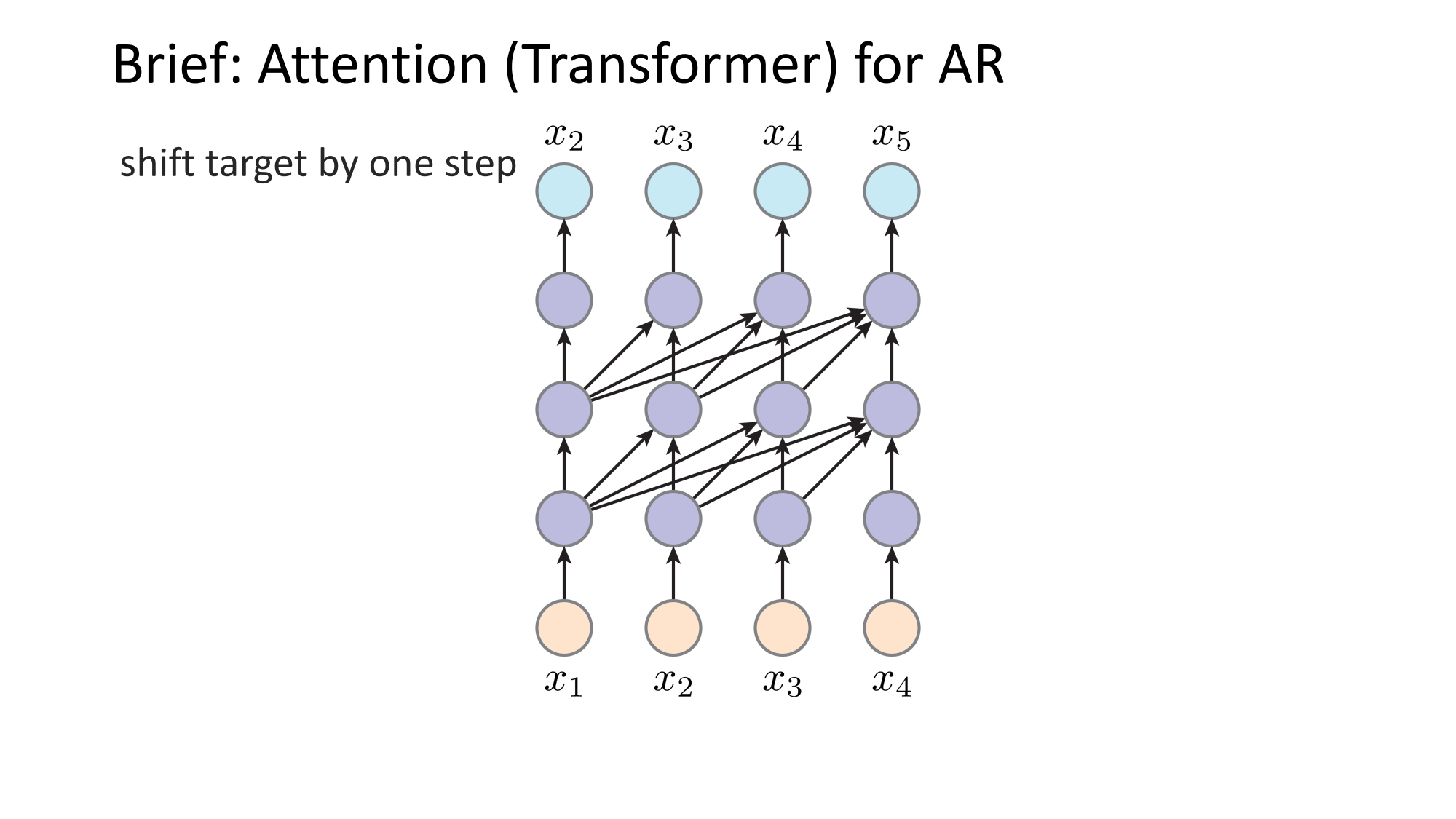
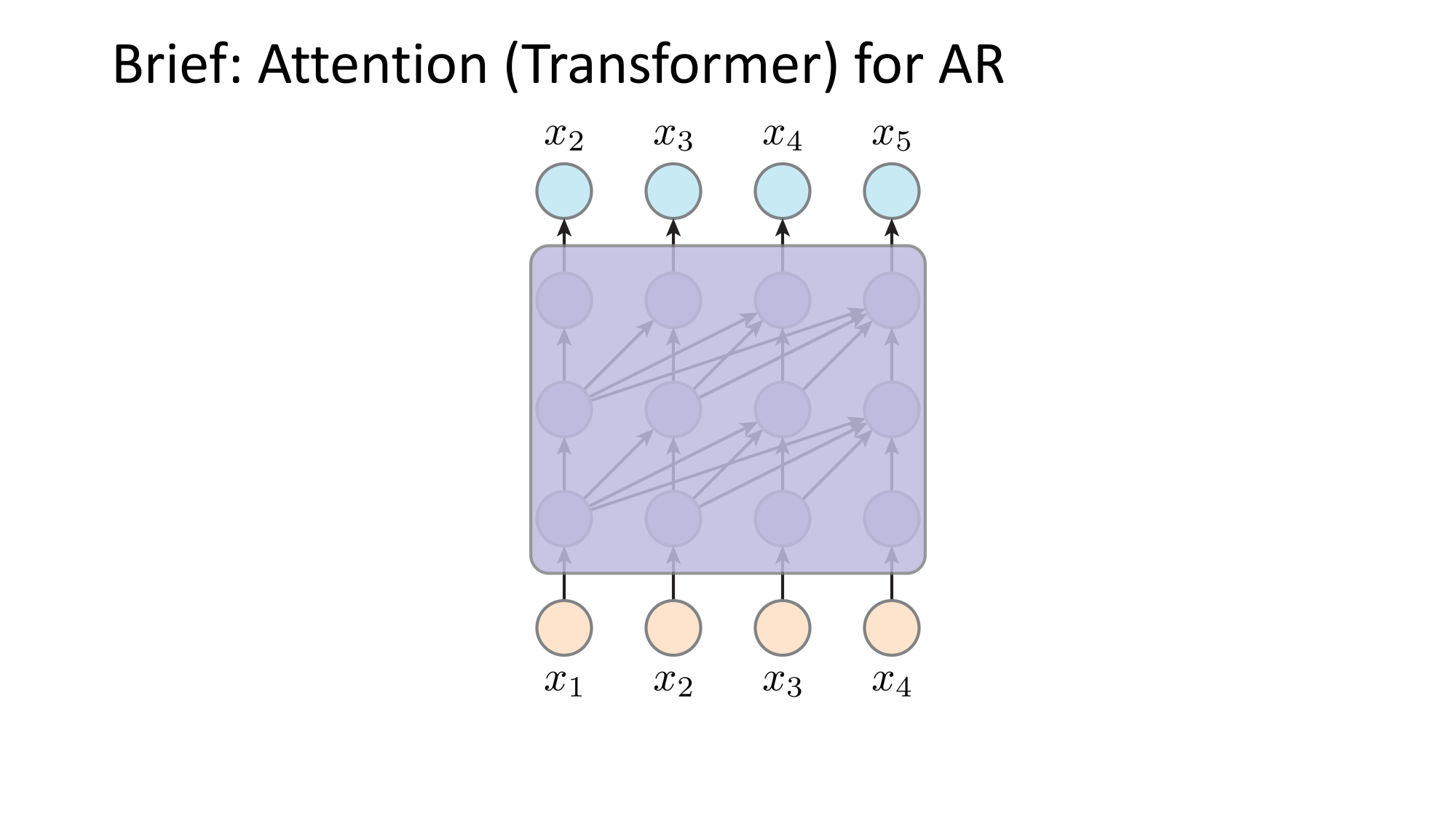
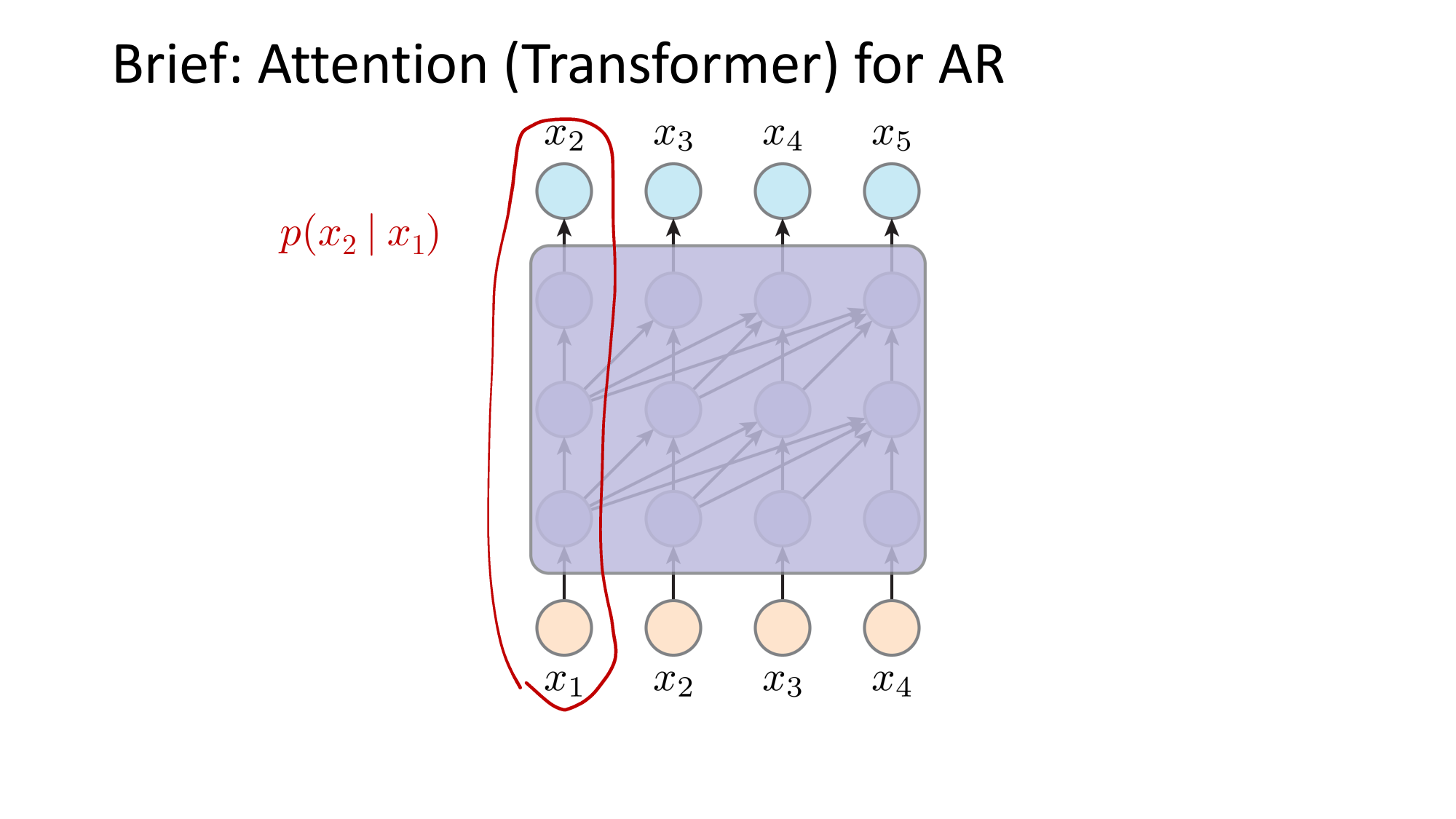
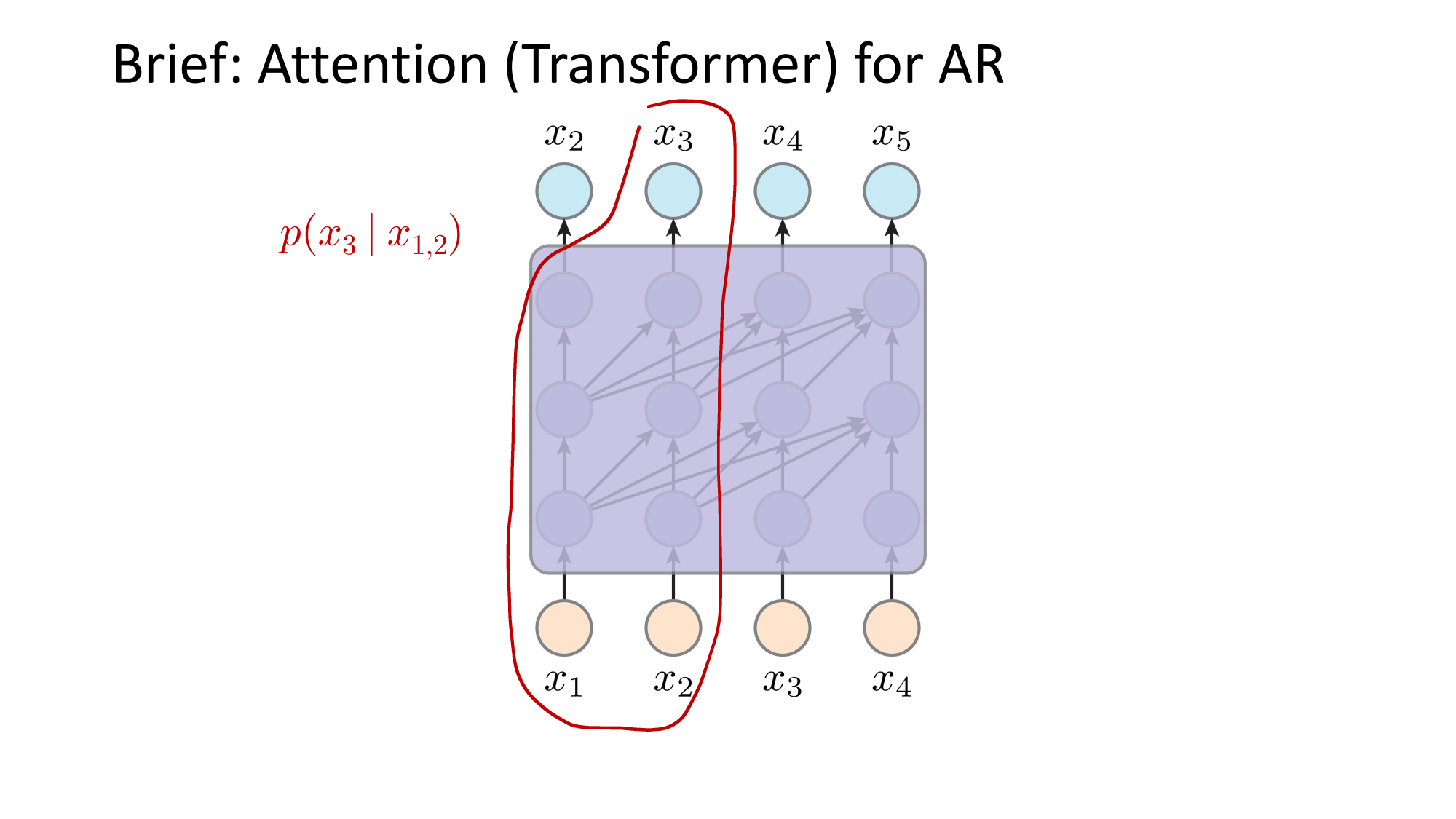
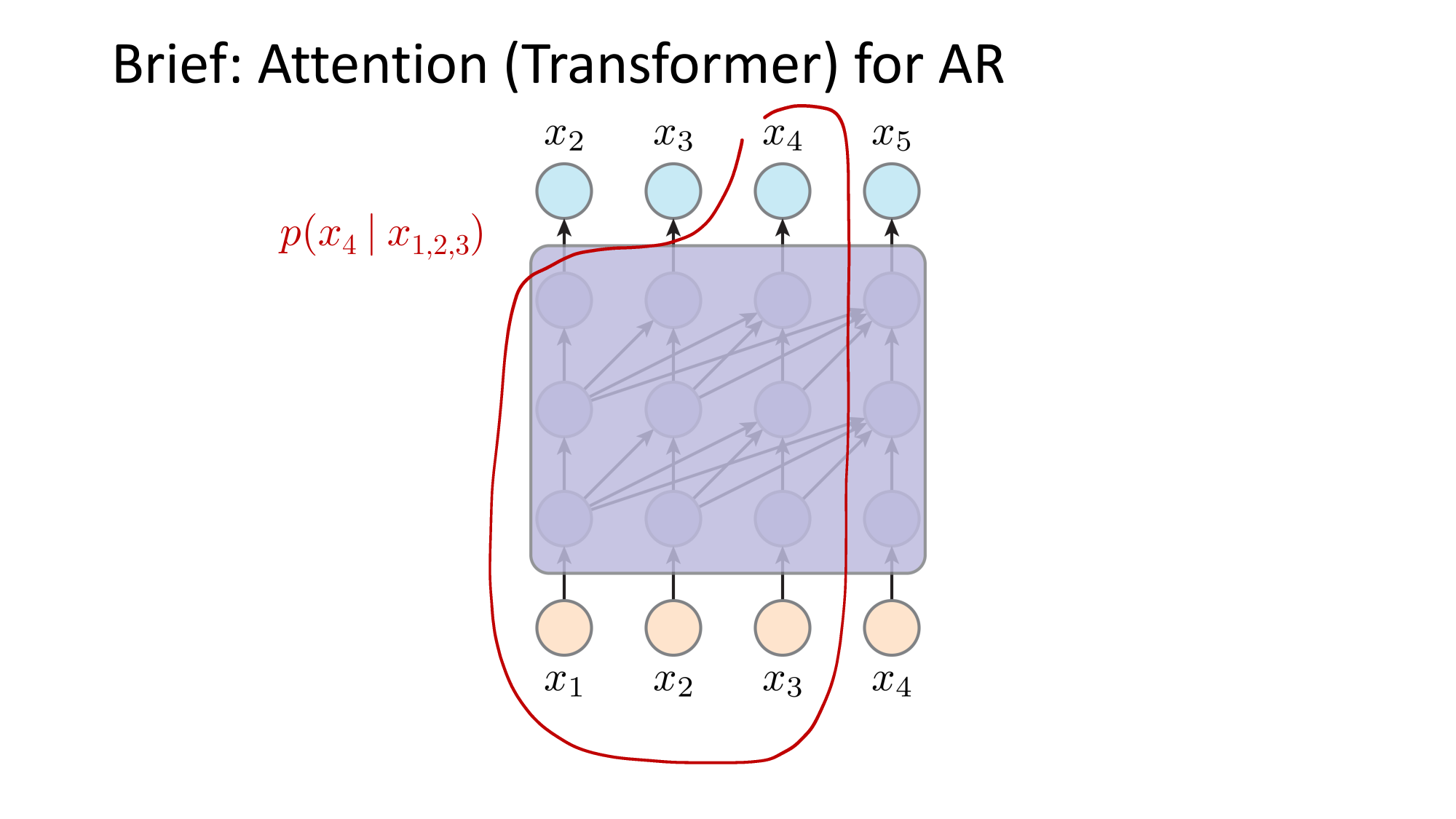
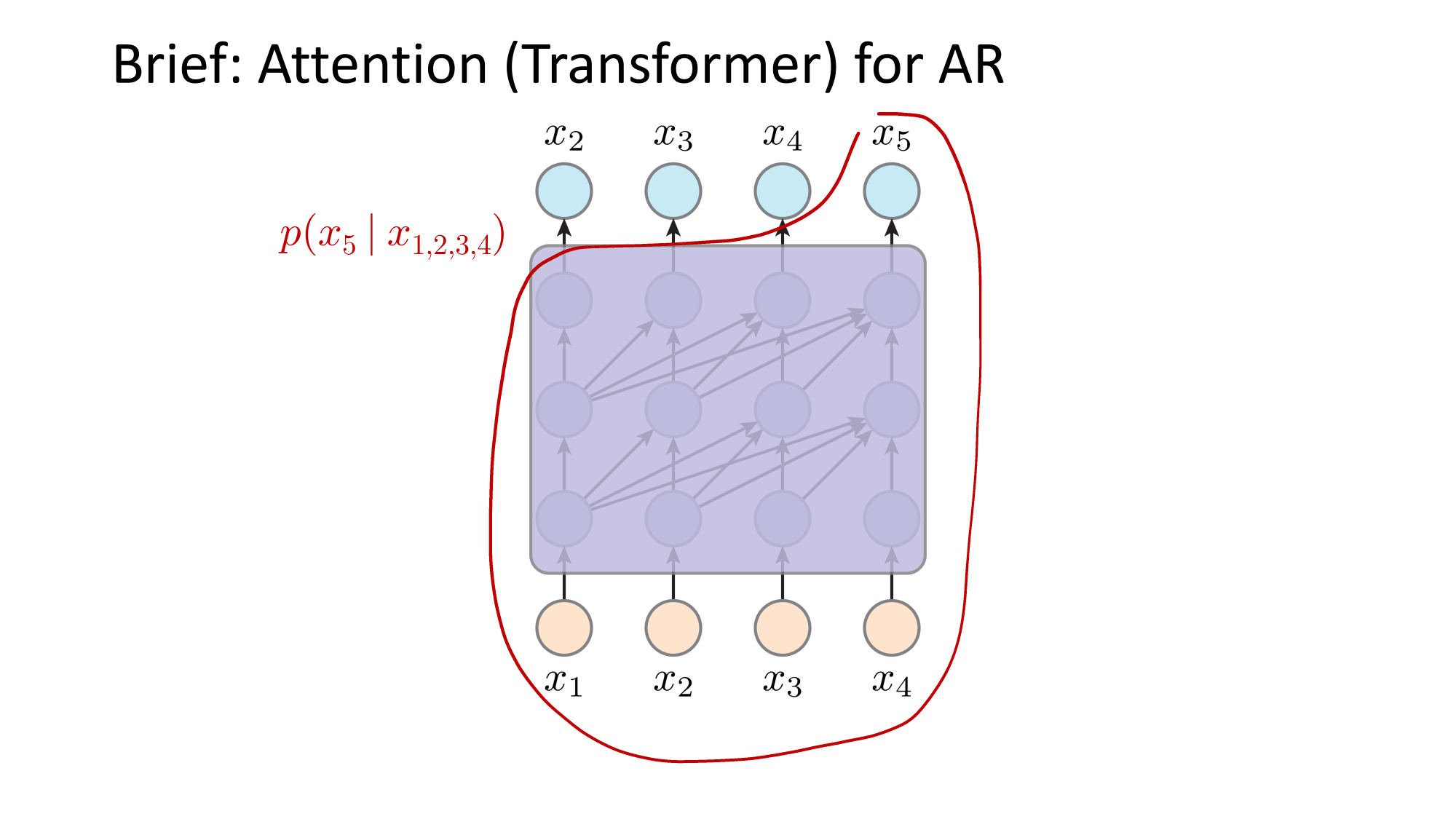

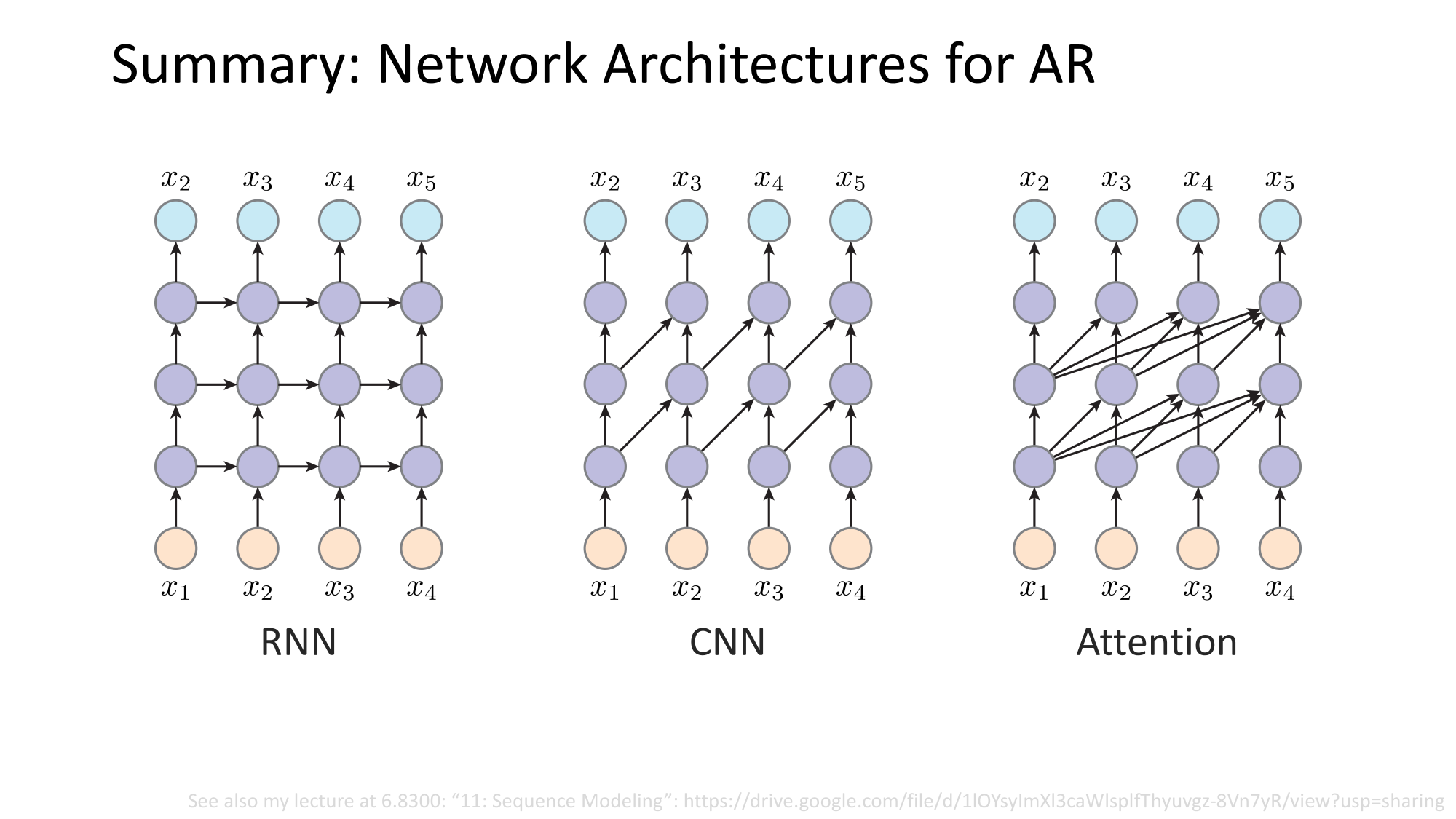
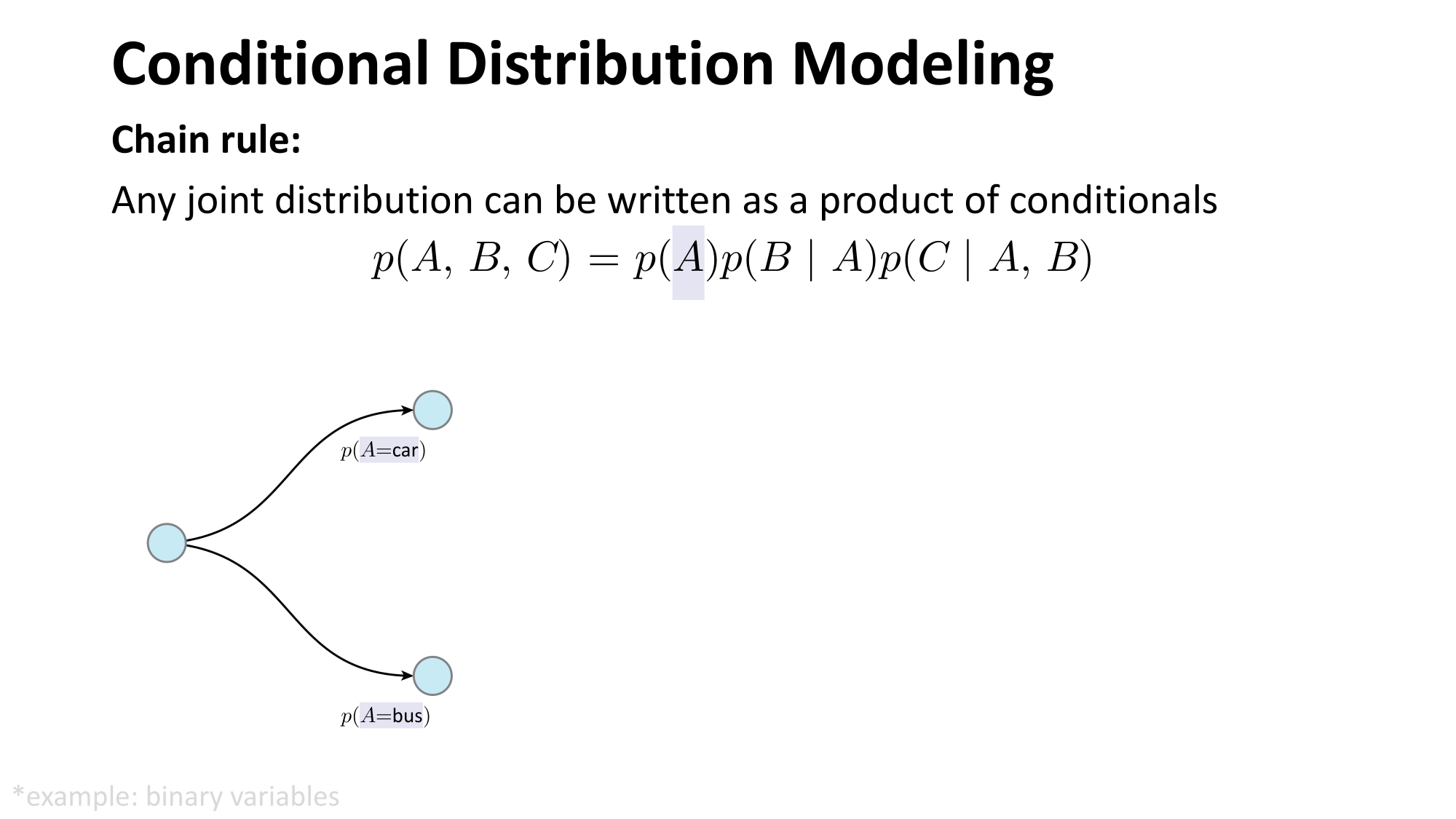
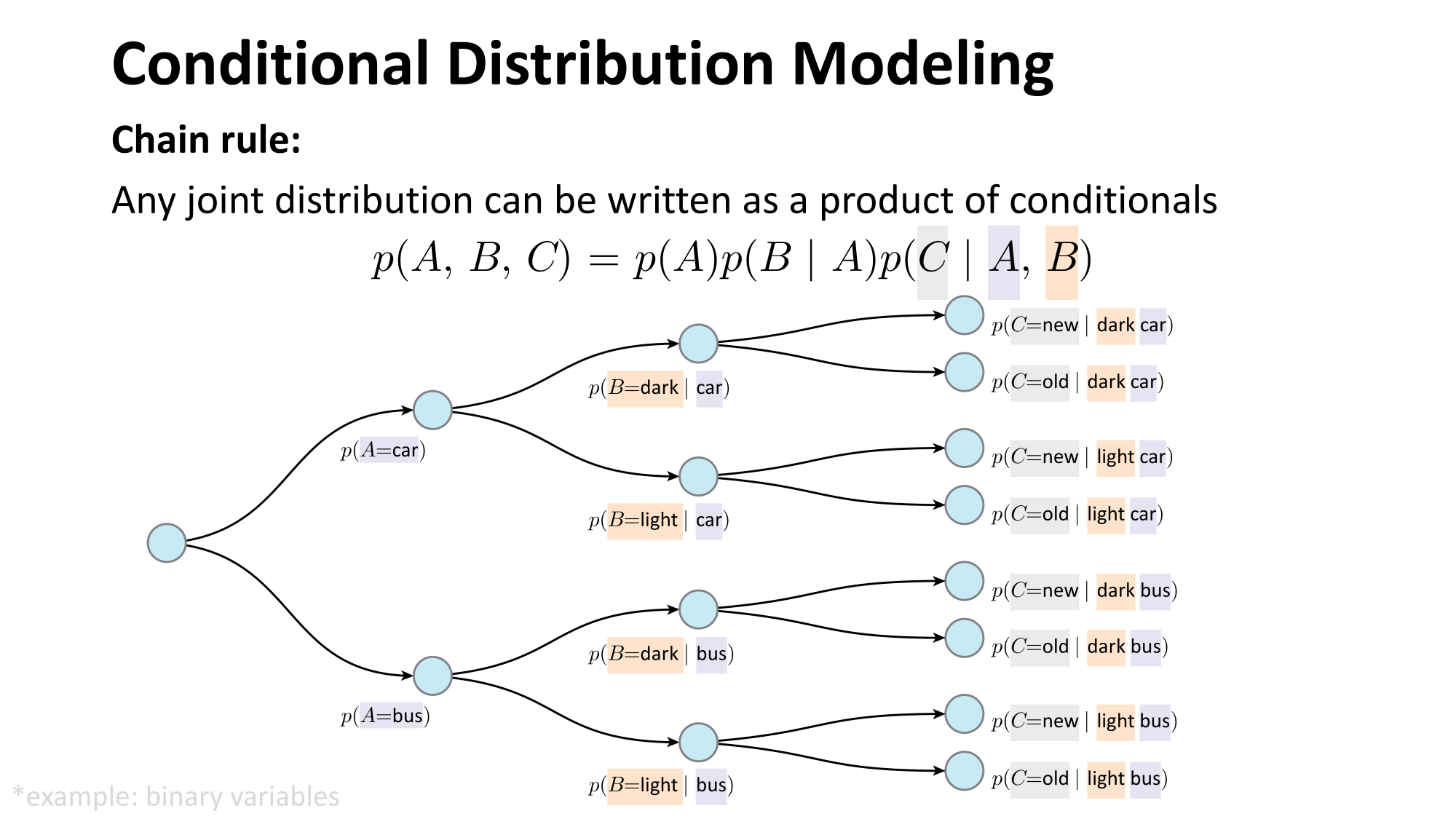
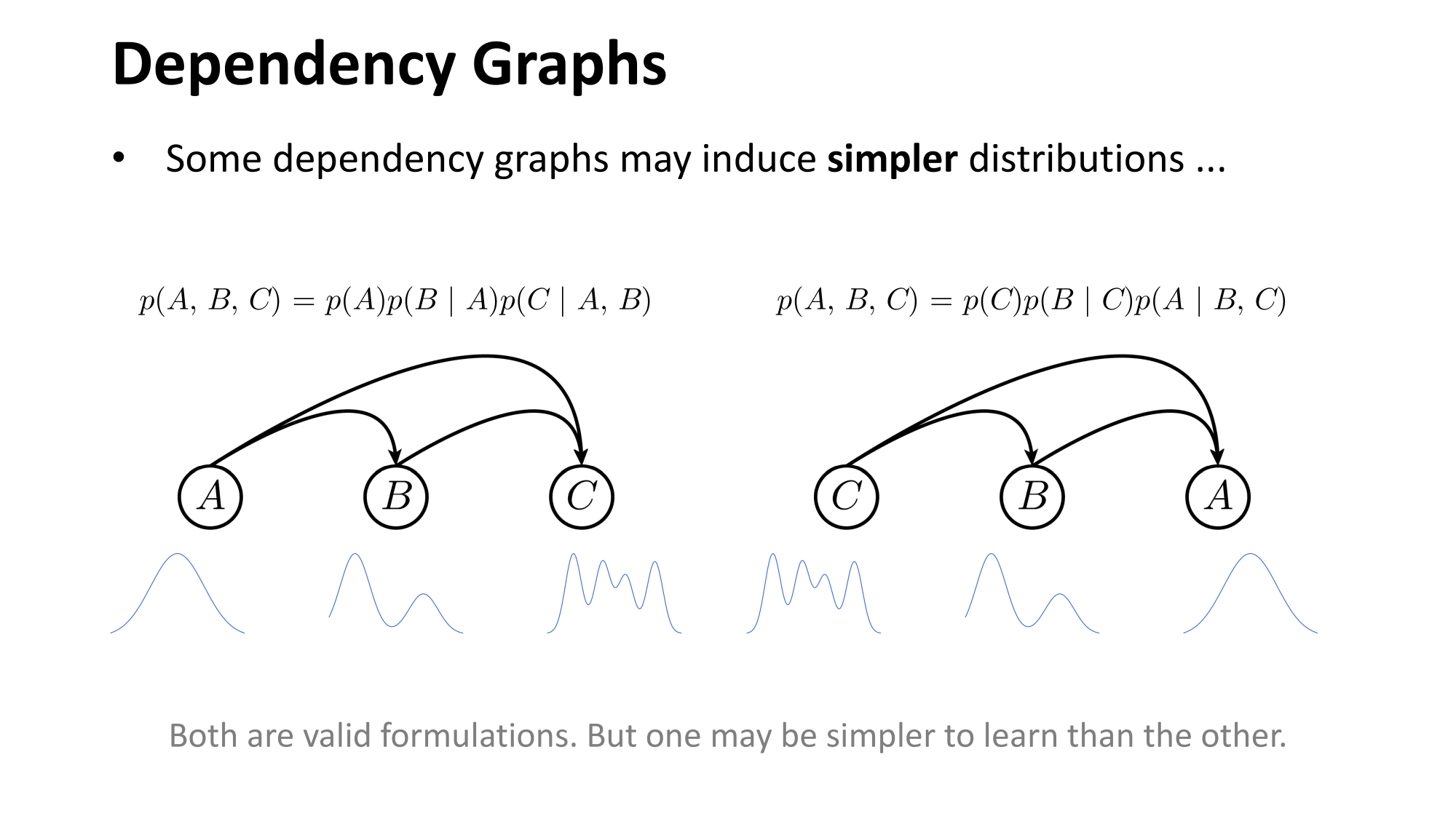
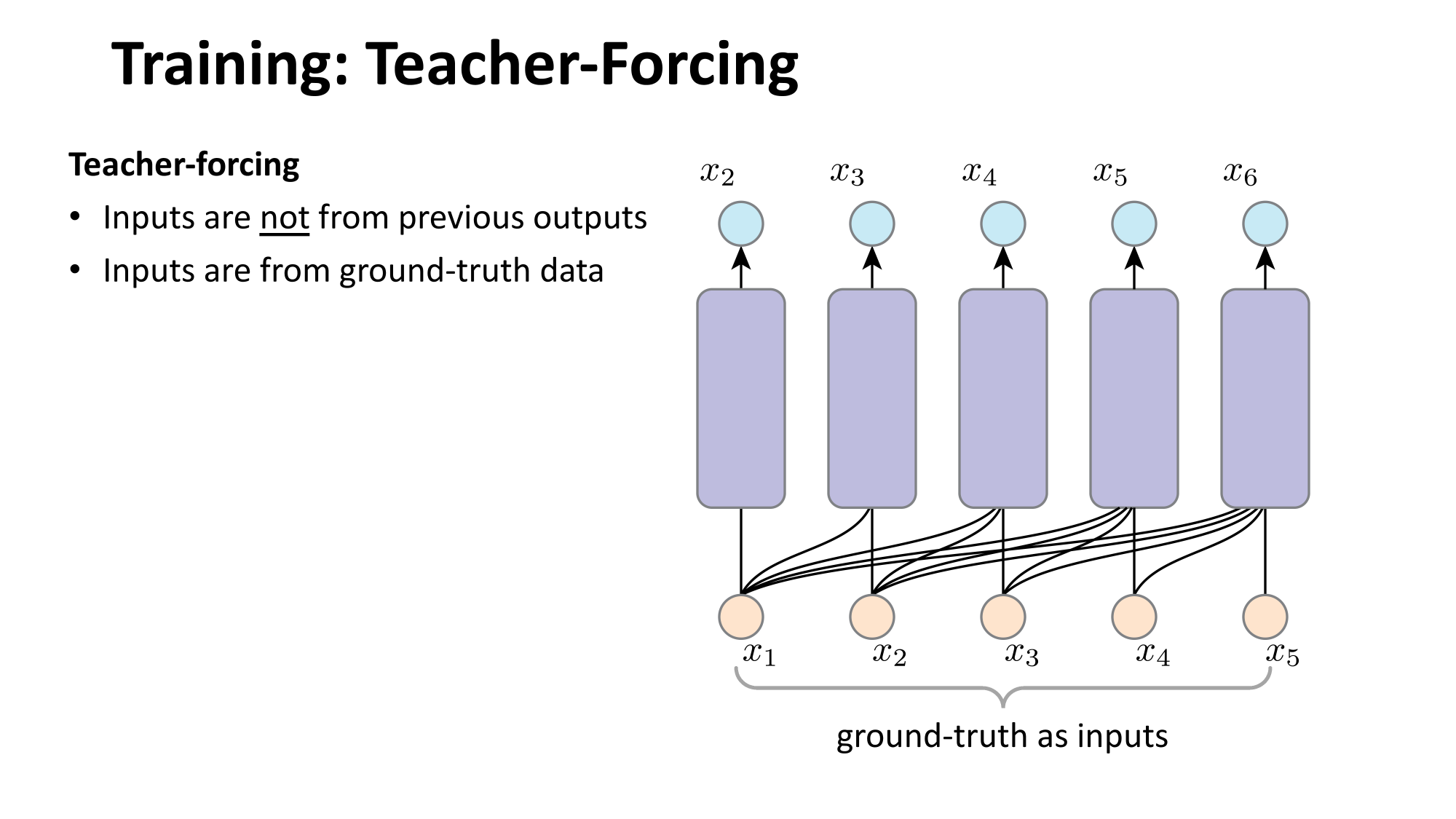
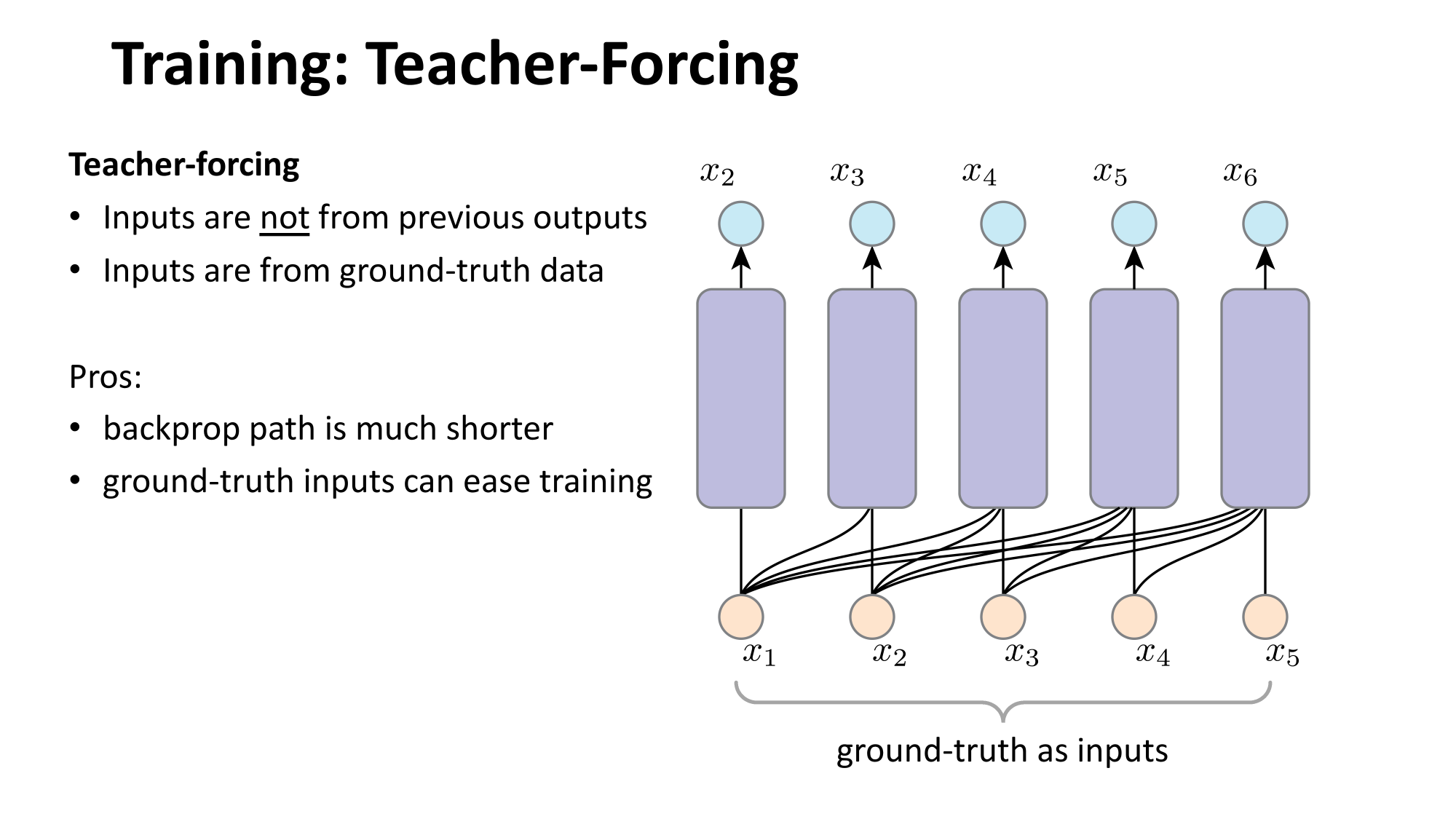
- Joint distribution \(\Rightarrow\) product of conditionals
- Inductive bias:
- shared architecture, shared weight
- induced order
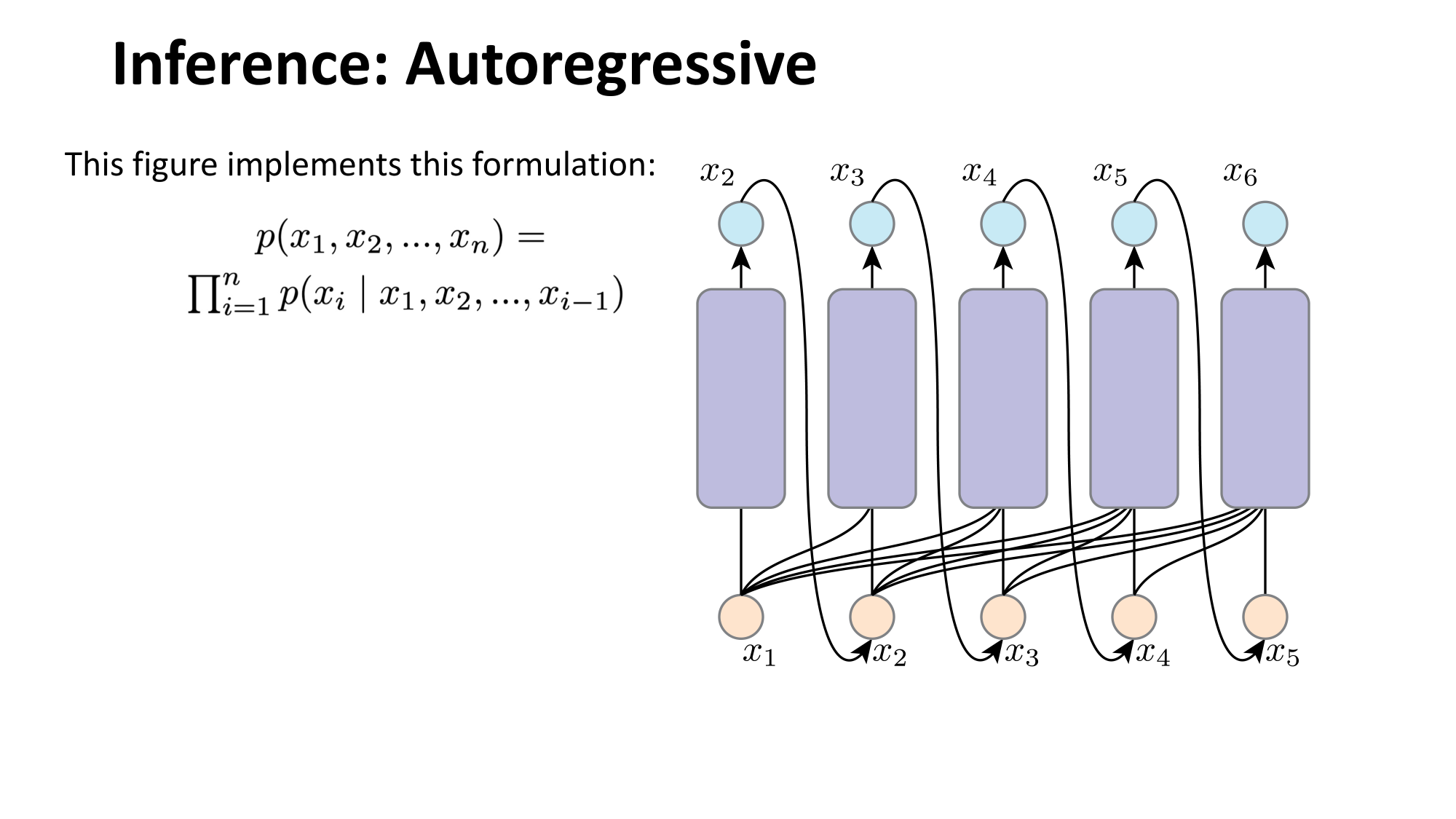
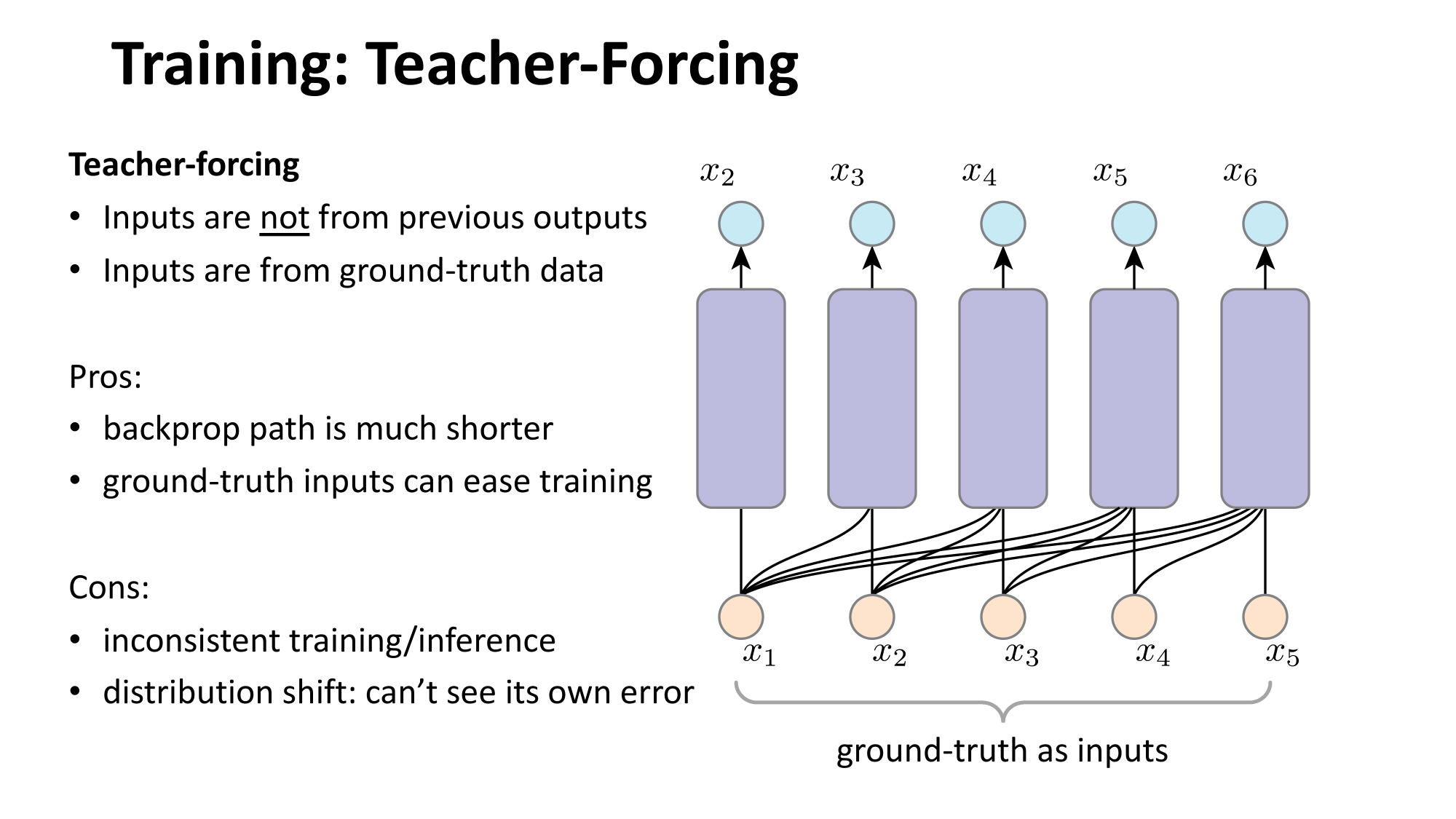
- Inference: autoregressive
Summary
How to represent \(x\), \(y\), and their dependence?
Financial Modeling (Quantitative Finance & Trading)
Autoregressive Models in Wireless Communications (Channel Modeling)
Structural Health Monitoring (Predictive Maintenance)
Energy Forecasting (Electrical Grid Load Prediction)
Network Traffic Modeling (Networking & Cybersecurity)
Deep Generative Models may involve:
- Formulation:
- formulate a problem as probabilistic models
- decompose complex distributions into simple and tractable ones
- Representation: deep neural networks to represent data and their distributions
- Objective function: to measure how good the predicted distribution is
- Optimization: optimize the networks and/or the decomposition
- Inference:
- sampler: to produce new samples
- probability density estimator (optional)
Thanks!
We'd love to hear your thoughts.



6.C011/C511 - ML for CS (Spring25) - Lecture 2 Generative Models - Autoregressive
By Shen Shen
6.C011/C511 - ML for CS (Spring25) - Lecture 2 Generative Models - Autoregressive
- 341



