Ender og ko-ender
Profunktorer
En morfi er en relasjon mellom objekter i en kategori
En profunktor mapper mellom ulike slike relasjoner:
- en global relasjon mellom objekter i kategorien
Eksempel: Hom-funktoren
Profunktorer er bifunktorer:
\mathbf{D}^\mathrm{op} \times \mathbf{C} \rightarrow \mathbf{Set}\\
\mathbf{C} \nrightarrow \mathbf{D}
Homfunktoren:
\mathbf{C}(-,=) :: \mathbf{C}^\mathrm{op} \times \mathbf{C} \rightarrow \mathbf{Set}
class Profunctor p where
dimap :: (c -> a) -> (b -> d) -> p a b -> p c d
f :: a \rightarrow b \\
P \langle f, \text{id}_b \rangle :: P\langle b, b \rangle \rightarrow P \langle a, b \rangle \\
P \langle \text{id}_a, f \rangle :: P\langle a, a \rangle \rightarrow P \langle a, b \rangle
f :: a -> b
dimap f id (p b b) :: p a b
dimap id f (p a a) :: p a bEksempel
Dinaturlige transformasjoner
https://bartoszmilewski.com/2017/03/29/ends-and-coends/
https://bartoszmilewski.com/2017/03/29/ends-and-coends/
Ender
Grenseverdi
a
b
f
I
F
\Delta_c
F a
F b
F f
c
C
\text{Funktor } F :: \mathbf{I} \rightarrow \mathbf{C} \\
\text{Kjegle} \in \mathbf{C} \\
\mathrm{Lim}\mathbf{C} = \text{apex i universell kjegle}
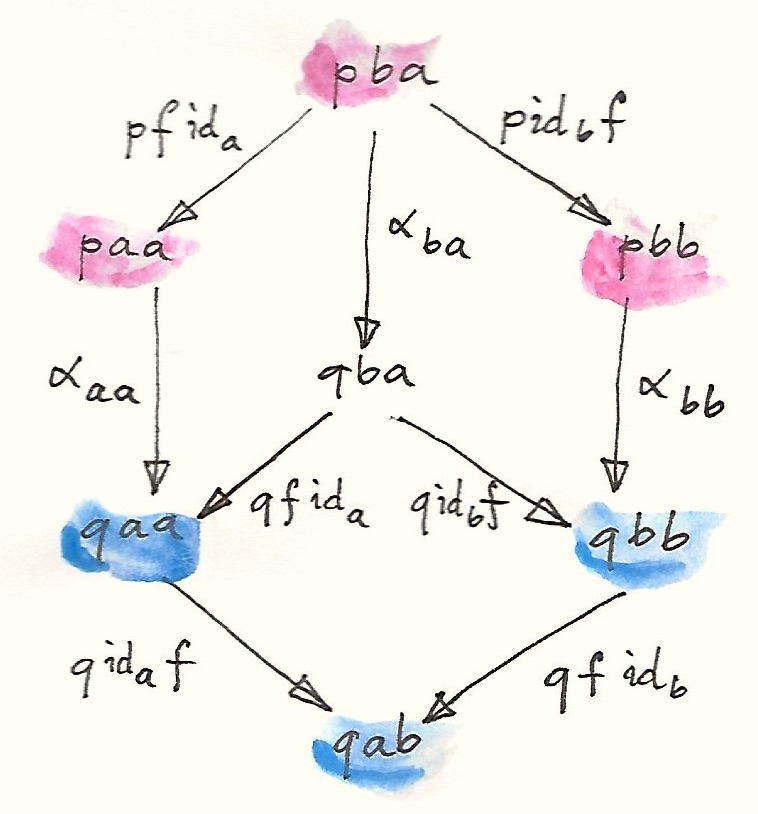
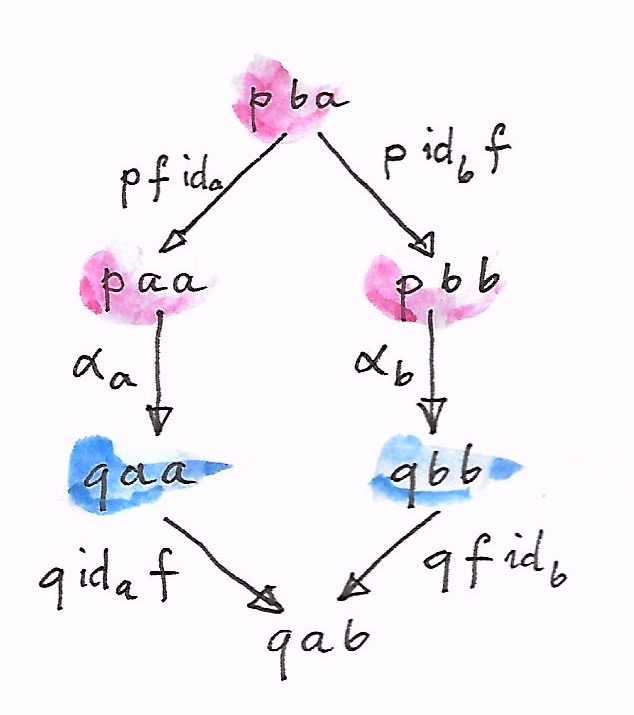
Kile
a
b
f
C
P
P a a
P b b
x
P a b
P id f
P f id
X
\text{Gitt profunktor } P :: \mathbf{C}^\mathrm{op} \times \mathbf{C} \rightarrow \mathbf{X} \\
\text{\textit{Kile}: Apex } x \in \mathbf{X} \text{ med dinaturlig transformasjon} \\
\alpha_a :: x \rightarrow P(a,a),
\text{ som kommuterer, slik at } \\
P(\mathrm{id}_a, f) \circ \alpha_a = P(f, \mathrm{id}_b) \circ \alpha_b \\
\alpha_a
\alpha_b
\circlearrowleft
Ende
\text{En \textit{ende} } \langle e, \pi \rangle \text{ er en \textit{universell} kile med}\\
\text{apex } e \text{ og transformasjon } \pi. \\
\text{Det vil si:}\\
\text{Gitt en dinaturlig } \theta_c :: x \rightarrow P(c,c)\\
\text{finnes unik } f :: x \rightarrow e \\
\text{slik at } \theta_c = \pi_c f
e
P(c,c)
\pi_c
x
\theta_c
f
\circlearrowleft
\text{Notasjon:}\\
e = \int_c F(c, c)\\
\pi_c: \int_x F(x, x) \rightarrow F(c,c)\\
I Haskell
{-# LANGUAGE RankNTypes #-}
import Data.Profunctor
-- for a given p, all diagonal elements p a a exist
type End p = forall a. p a a
-- given a profunctor p, an a and an End for p,
-- you can extract p a a
pi :: Profunctor p => forall a. (End p) -> p a a
pi e = e
-- Wedge condition
-- dimap f id . pi = dimap pi . f id
main :: IO ()
main = do
print $ Main.pi id 1Ender som equalizers
\pi_a
e
P(a,a)
\pi_b
P(b,b)
P(a,b)
\lambda_P
\varrho_P
\circlearrowleft
https://bartoszmilewski.com/2015/04/15/limits-and-colimits/
Naturlige transformasjoner som ender
\text{Naturlige transformasjener mellom } F \text{ og } G \\
\text{er en delmengde av hom-mengden } \mathbf{C}(F a, G b)\\
\langle a, b \rangle \rightarrow \mathbf{C}(F a, G b)\\
\\ \text{er en profunktor}
\int_c \mathbf{C}(F c, G c)
\pi_a
\pi_b
\mathbf{C}(F a, G a)
\mathbf{C}(F b, G b)
\mathbf{C}(F a, G b)
\mathbf{C}(\mathrm{id}_a, G f)
\mathbf{C}(F f, \mathrm{id}_b)
\text{Velg et element } \tau \text{ fra } \int_c\mathbf{C}(Fc, Gc)\\
\text{Det projiseres til}\\
\tau_a :: F a \rightarrow G a \\
\tau_b :: F b \rightarrow G b \\
\mathbf{C}(\mathrm{id}_a, G f) \tau_a = G f \circ \tau_a \circ \mathrm{id}_a \\
\mathbf{C}(F f, \mathrm{id}_b) \tau_b = \mathrm{id}_b \circ \tau_b \circ F f \\
\Rightarrow\\
\text{kilevilkåret} = \text{naturlighetskvadraten for } \tau
\text{Det vil si at } \int_c \mathbf{C}(Fc, Gc)\\
\text{tilsvarer mengden av naturlige transformasjoner} \\
\text{mellom } F \text{ og } G
Ko-ender
- Snu alle pilene
- projeksjoner blir injeksjoner
- bytt plass på lambda og rho
- Equalizer -> coequalizer
- Generalisering av koprodukt
i_a
P(a,a)
i_b
P(b,b)
P(a,b)
\lambda_P
\varrho_P
\circlearrowleft
\int^x P(x,x)
-- exists a. p a a
{-# LANGUAGE ExistentialQuantification #-}
data Coend p = forall a. Coend (p a a)
{-# LANGUAGE RankNTypes #-}
data End p = End (forall a. p a a)Coequalizer
In category theory, a coequalizer ... is a generalization of a quotient by an equivalence relation to objects in an arbitrary category. (Wikipedia)
Ekvivalens-relasjon
a \sim a
\text{if } a \sim b \text{ then } b \sim a
\text{if } a \sim b \text{ and } b \sim c \text{ then } a \sim c
refleksiv
symetrisk
transitiv
[a] := \left\{ x \in X\,|\, a \sim x\right\}
ekvivalens-klasse
kvote
X/\!\sim\; := \{ [x]\,|\,x \in X\}
Eksempel
a, b, c, d \in \mathbb{Z} \\
(a,b)\sim(c,d) \text{ iff } \frac a b = \frac c d
Rasjonale tall er ekvivalensklasser for denne ekvivalensen
\mathbb{Z} \times \mathbb{Z}\, /\! \sim \; = \mathbb{Q}
\text{Koenden er en coequalizer for } \lambda \; \text{og} \; \varrho . \\
\text{Gitt } P(a, b) \; \text{og} \; f :: a \rightarrow b \\
\text{finner den ekvivalente elementer i } \int_c P(c, c)
i_a
P(\frac 1 2, \frac 1 2)
i_b
P(\frac 2 4, \frac 2 4)
P(\frac 1 2,\frac 2 4)
\lambda_P
\varrho_P
\circlearrowleft
\int^x P(x,x) = \vee [\frac 1 2,\frac 2 4, \frac 4 8, \ldots], [\frac 1 3, \frac 3 9 \ldots], \ldots
P (a,b) \Leftrightarrow \;\sim\\
\int^x P(x,x) = \mathbb Q
\mathbf{Set} \left( \int^x\!\!P(x,x), \,c \right) \cong \int_x \mathbf{Set} \bigl(P(x,x),\,c\bigr)
\text{Hom-mengden mellom } \int^x P(x,x) \text{ og et objekt } c \\
\text{er ekvivalent/isomorf med \textit{enden} av } \\
\text{Hom-mengden mellom } P(x,x) \text{ og } c
Kontinuerlighet
(exists x. p x x) -> c ≅ forall x. p x x -> cParametrisk polymorfi (produktet av alle funksjoner)
Funksjon som tar en sumtype som er summen av alle typer
\mathbf{Set} \left( \int^x\!\!P(x,x), \,c \right) \cong \int_x \mathbf{Set} \bigl(P(x,x),\,c\bigr)
Ninja Yoneda Lemma
\int_z \mathbf{Set}\bigl(\mathbf{C}(a,z), F z\bigr) \cong F a \\
\;\\
\int^z \mathbf{C}(z,a) \times F z \cong F a\\
\;\\
\int \delta(z-a) f(z) dz= f(a)
Sammensetning
(Q \circ P)(a,b) = \int^c P(c,a) \times Q(b, c)
data Procompose q p a b where
Procompose :: q a c -> p c b -> Procompose q p a b
exists c. (q a c, p c b)Ender og koender
By Simon Mitternacht
