Topoi
Bilder fra https://bartoszmilewski.com/2017/07/22/topoi/
Vi har brukt mengder som assembly for vår kategoriteori, ikke sikkert det er det beste eller mest naturlige
Hva med å bruke rom i stedet? De har mere struktur enn mengder og kan formuleres uavhenig av mengdeteori.
Rom, mengder og delmengder er viktige begrep innen topologi
Man kan formulere topologi gjennom kategorier av typen topos i stedet for Set
En topos har blant annet delobjekter, som er en generalisering av delmengder
Delmengder som funksjoner
\text{En vilkårlig funksjon}\;f :: a \rightarrow b\\
\text{definerer en delmengde av}\;b\\
\text{som er bildet av}\;a\;\text{under}\;f
\text{Vi krever at}\;f\;\text{skal være injektiv}
\text{En annen injektiv funkjson}\;f^\prime::a^\prime\rightarrow b\\
\text{kan definere samme delmengde}
\text{Vi sier at}\;f\;\text{og}\;f^\prime\;\text{er ekvivalente}\\
\text{hvis det finnes en}\;h::a\rightarrow a^\prime\;\\
\text{slik at}\;f = f^\prime \circ h
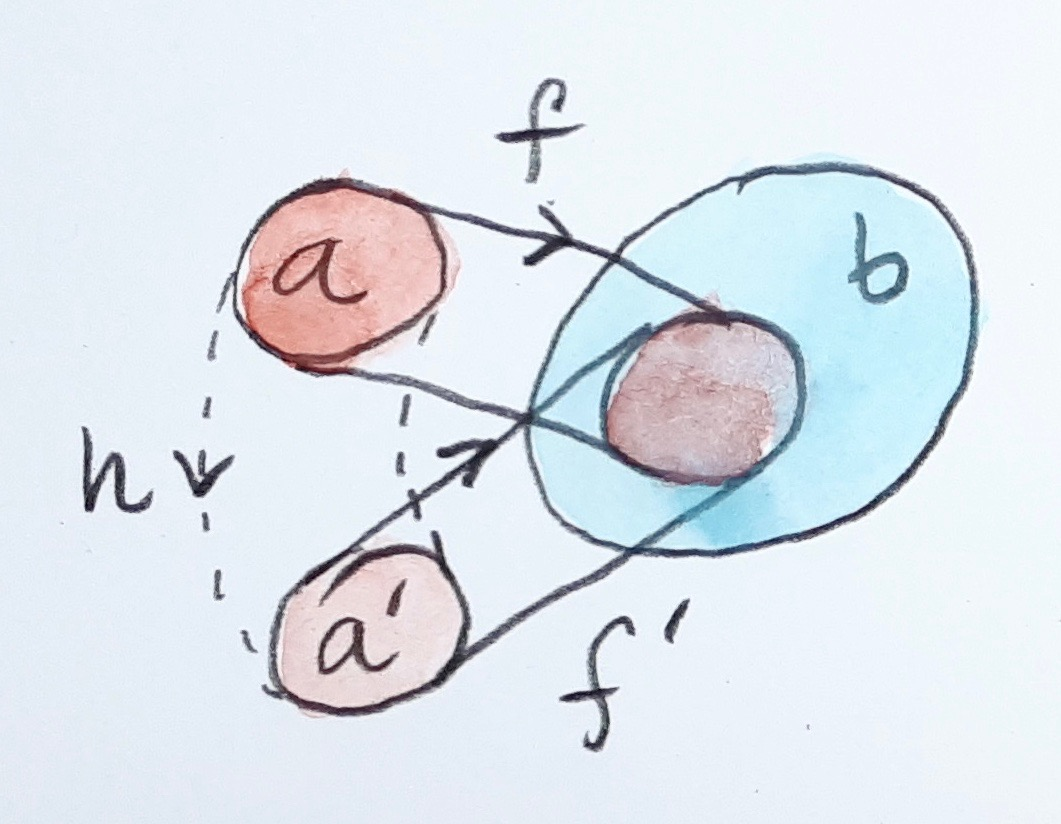
\text{Generalisere injektive funksjoner til \textit{monomorfier}}
m\;\text{er en monomorfi hvis}\\
g::c\rightarrow a\\
g^\prime::c\rightarrow a\\
\text{og}\\
m \circ g = m \circ g^\prime\quad\Rightarrow\quad g = g^\prime
Delmengder som karakteristiske funksjoner
\text{Karakteristisk funksjon for delmengde}\;s\subseteq b\;\\
\,\\
\chi_s::b\rightarrow \Omega\\
\,\\
\Omega = \{0, 1\} \Leftrightarrow \{\mathrm{true}, \mathrm{false}\}\\
\chi_s(x) = 1\;\text{hvis}\;x\in s\\
\chi_s(x) = 0\;\text{hvis}\;x\notin s
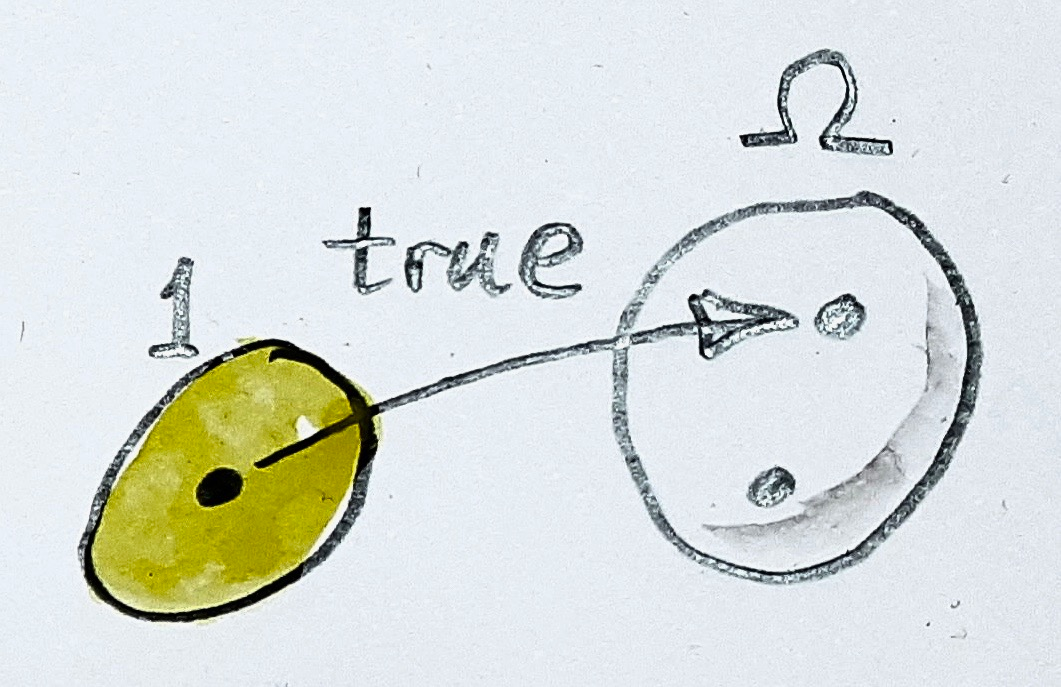
\text{Hva er true? (uten å kikke inn i}\;\Omega)
\mathrm{true} :: 1 \rightarrow \Omega\quad\text{(monomorfi)}
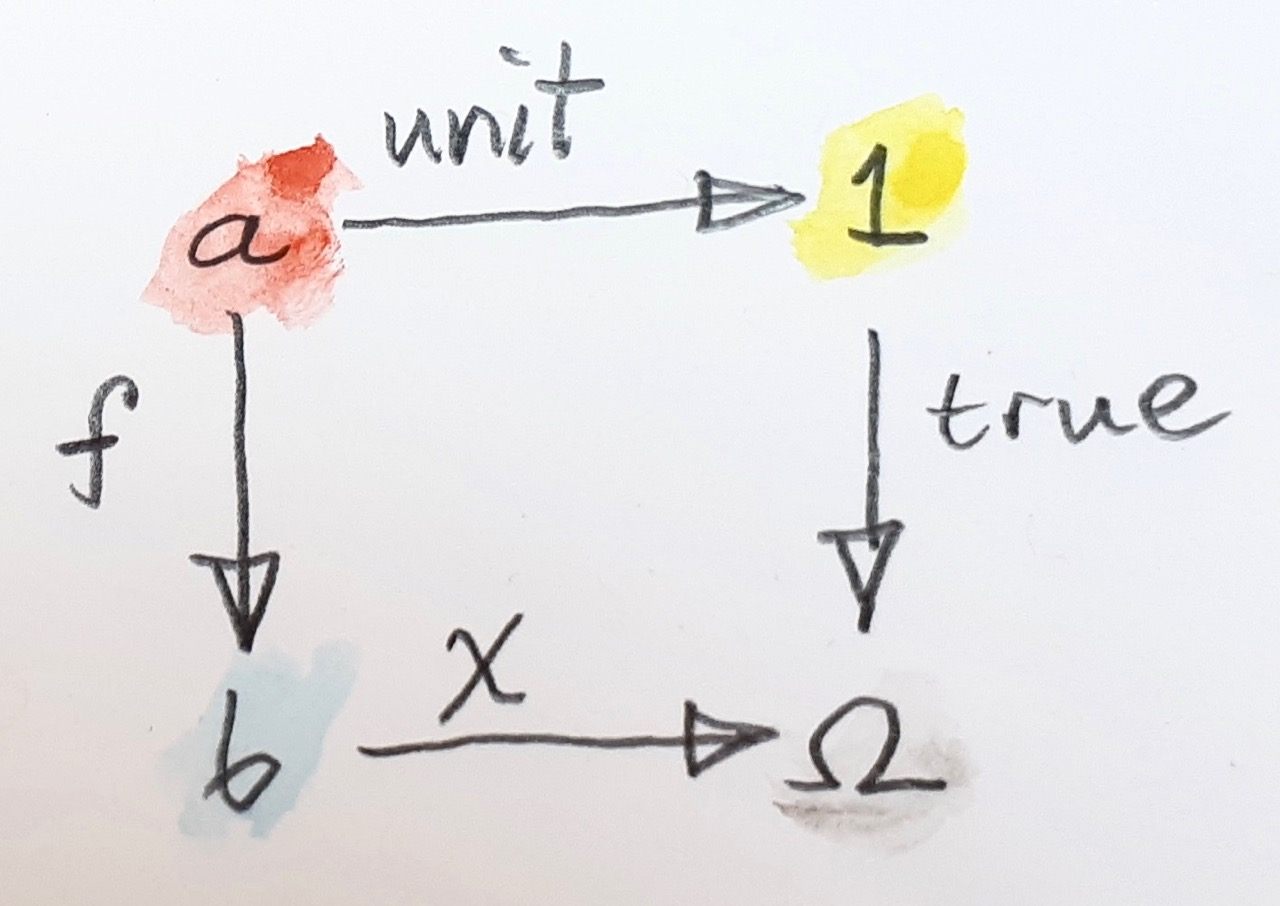
\text{Pullback av true langs}\;\chi\;\\
\text{definerer både}\;a\;\text{og}\;f
a\;\text{fordi den er universell}\\
f\;\text{fordi alt annet allerede er definert}

\mathrm{true}\circ\mathrm{unit}=\chi\circ f\\
\,\\
\mathrm{true}\circ\mathrm{unit}\;\text{mapper alle}\\
\text{elementer i}\;a\;\text{til ``true''}\\
\text{Derfor må}\;f\;\text{mappe til}\\
\text{de elementer i}\;b\;\text{hvor}\\
\chi\;\text{er ``true''}
\text{Siden pullbacken er universell er}\;f\;\text{injektiv (?)}
\text{I andre kategorier enn}\;\mathbf{Set}\;\text{kreves:}\\
\checkmark\;\text{terminalt objekt}\;(\mathbf 1)\\
\checkmark\;\text{alle finite grenseverdier eksisterer (pullback)}\\
I en generell kategori

\text{Da defineres}\;\Omega\;\text{av egenskapen:}\\
\text{For hver monomorfi}\;f\;\text{finnes en unik morfi}\;\chi\\
\text{som gør at pullback-diagrammet kommuterer}

\text{Tidligere hadde vi}\;\Omega,\;b\;\text{og}\;\mathbf{1}\\
\text{og søkte}\;a\;\text{og}\;f\\
\text{I det generelle fallet har vi}\;a\;\text{og}\;b,\\
\text{og søker}\;\Omega\;\text{og true.}\\
\text{De ekisterer bare om det finnes en monomorfi}\;f\\
\text{som er en pullback av en unik}\;\chi

f\;\text{er kun unik opp til isomorfi}\\
\mathrm{Sub}(b):=\text{mengden av subobjekter i}\;b\\
\mathrm{Sub}(b) \cong \mathbf{C}(b,\Omega)\\
\mathrm{Sub}(-)\;\text{er en kontravariant representerbar funktor}\\
Topos
Et topos er en kategori som er:
- Kartesisk lukket: Har alle produkter, et terminalobjekt og eksponentialer (høyreadjunkt til produkt)
- Har grenseverdier for alle finite diagrammer
- Har en "delobjekt-klassifikator" Ω
Topoi og logikk
- I et topos kan et predikat generaliseres til en morfi fra a til Ω
- Topoi innholder alle byggeblokkene for logikk
- produkt - og
- koprodukt - eller
- eksponential - implikasjon
- Alle aksiomer utenom Loven om den ekskluderte tredje holder:
- Det finnes påstander som vi ikke kan vite om de er falske eller sanne (intuisjonistisk/konstruktiv logikk)
- Beslektet med beregninger som ikke kan fullføres
Topoi
By Simon Mitternacht
Topoi
- 412



