\text{Chapter 21}

\text{Chapter 22}

\text{\&}

q_1

q_2

q_3

5.00 \text{ cm}

3.00 \text{ cm}

4.00 \text{ cm}

\vec{F}

\text{Three point charges are placed as shown in Figure 2. The magnitude of $q_1$ is $5.00 \mu \mathrm{C}$ but its }

\text{sign is not known. The charge $q_2$ is not known while charge $q_3$ is $+7.00 \mu \mathrm{C}$. The net force $\overrightarrow{\boldsymbol{F}}$}

\text{on $q_3$ is in the negative $x$-direction.}

\text{Calculate the magnitudes of $q_2$ and the force $\overrightarrow{\boldsymbol{F}}$, respectively?}

\text{A) $2.11 \hspace{1mm}\mu \mathrm{C}, 246 \mathrm{~N}$}

\text{B) $1.22\hspace{1mm} \mu \mathrm{C}, 164 \mathrm{~N}$}

\text{C) $5.51 \hspace{1mm}\mu \mathrm{C}, 291 \mathrm{~N}$}

\text{D) $3.65 \hspace{1mm}\mu \mathrm{C}, 462 \mathrm{~N}$}

\text{E) $3.05 \hspace{1mm}\mu \mathrm{C}, 299 \mathrm{~N}$}

\text { Since } \mathrm{F} \text { is towards left, } q_3 \text { is +ve, } q_1 \text { is }-\mathrm{ve} \text { and } q_2 \text { is +ve }

\sin\theta_1=\frac{3}{5} ; \quad \sin\theta_2=\frac{4}{5}

F_y=0=k q_3\left(\frac{|q_2|}{(0.03)^2} \times \sin \theta_2-\frac{|q_1|}{(0.04)^2} \times \sin \theta_1\right)=0

|q_2|=|q_1| \times\left(\frac{0.03}{0.04}\right)^2 \times \frac{\sin \theta_1}{\sin \theta_2}=5 \times 10^{-6} \times\left(\frac{0.03}{0.04}\right)^2 \times \frac{3 / 5}{4 / 5}

q_2=2.11 \mu\mathrm{C}

|F|=k q_3\left[\frac{|q_2|}{(0.03)^2} \cos \theta_2+\frac{|q_1|}{(0.04)^2} \cos \theta_1\right]

=9 \times 10^9 \times 7 \times 10^{-6}\left[\frac{2.11\times 10^{-6}}{(0.03)^2} \times \frac{3}{5}+\frac{5\times 10^{-6}}{(0.04)^2} \times \frac{4}{5}\right] =246.12 \mathrm{~N}

q_1

q_2

q_3

5.00 \text{ cm}

3.00 \text{ cm}

4.00 \text{ cm}

\vec{F}

\text{Three point charges are placed as shown in Figure 2. The magnitude of $q_1$ is $5.00 \mu \mathrm{C}$ but its }

\text{sign is not known. The charge $q_2$ is not known while charge $q_3$ is $+7.00 \mu \mathrm{C}$. The net force $\overrightarrow{\boldsymbol{F}}$}

\text{on $q_3$ is in the negative $x$-direction.}

\text{Calculate the magnitudes of $q_2$ and the force $\overrightarrow{\boldsymbol{F}}$, respectively?}

\theta_1

\theta_2

\theta_1

\theta_2

\theta_1

\text{Charges $-q$ and $+2 q$ in Figure 3 are located at $x= \pm a$. If $\mathrm{q}=5.00 \hspace{1mm}\mathrm{pC}$ and $a=10.0$ $\mathrm{cm}$,}

\text{find the magnitude of the net electric field at point $\boldsymbol{P}$ due to these charges.}

\cdot

a

2a

-q

x

y

2a

2q

\text{A) $1.45 \mathrm{~N} / \mathrm{C}$}

\text{B) $1.01 \mathrm{~N} / \mathrm{C}$}

\text{C) $2.55 \mathrm{~N} / \mathrm{C}$}

\text{D) $3.05 \mathrm{~N} / \mathrm{C}$}

\text{E) $4.45 \mathrm{~N} / \mathrm{C}$}

P

\text{Charges $-q$ and $+2 q$ in Figure 3 are located at $x= \pm a$. If $\mathrm{q}=5.00 \mathrm{pC}$ and $a=10.0$ $\mathrm{cm}$,}

\text{find the magnitude of the net electric field at point $\boldsymbol{P}$ due to these charges.}

\cdot

a

2a

-q

x

y

2a

2q

\text{in this isosceles triangle, we have:}

\theta=\tan^{-1}\frac{2a}{a}=63.4^0

E_x=\frac{k \times(2 q+q)}{5 a^2} \times \cos 63.4=\frac{9 \times 10^9 \times 3 \times 5 \times 10^{-12}}{5 \times(0.1)^2} \times \cos 63.4=1.209 \mathrm{~N} / \mathrm{C}

E_y=\frac{k \times(2 q-q)}{5 a^2} \times \sin 63.4=\frac{9 \times 10^9 \times 5 \times 10^{-12}}{5 \times(0.1)^2} \times \sin 63.4=0.805 \mathrm{~N} / \mathrm{C}

E_x=E^1_x+E_x^2=E^1\cos(\theta)+E^2\cos{(\theta)}

=k\frac{2q}{(\sqrt{5}a)^2}\cos \theta+k\frac{q}{(\sqrt{5}a)^2}\cos\theta

\sqrt{5}a

\theta

\theta

\theta

\theta

E=\sqrt{E_x^2+E_y^2}=\sqrt{1.21^2+0.81^2}=1.45 \hspace{1mm}N/C

\text{A proton moving with a velocity $\overrightarrow{\boldsymbol{v}}=3.80 \times 10^6 \mathrm{~m} / \mathrm{s}\hspace{1mm} \hat{\boldsymbol{i}}$ enters a region $(x \geq 0)$ containing }

\text{a uniform electric field $\overrightarrow{\boldsymbol{E}}=-5.60 \times 10^4 \mathrm{~N} / \mathrm{C} \hspace{1mm}\hat{\boldsymbol{i}}$. How far will the proton travel in this region }

\text{before it momentarily stops?}

\text{A) 1.35 m}

\text{B) 0.221 m}

\text{C) 0.562 m}

\text{D) 2.42 m}

\text{E) 0.770 m}

a=\frac{q E}{m_p}=\frac{1.6 \times 10^{-19} \times\left(-5.6 \times 10^4\right)}{1.67 \times 10^{-27}}=-5.365 \times 10^{12} \mathrm{~m} / \mathrm{s}

X=\frac{v_f^2-v_i^2}{2 a}=\frac{-v_i^2}{2 a}=\frac{-\left(3.80 \times 10^6\right)^2}{2 \times\left(-5.365 \times 10^{12}\right)}=1.346 \mathrm{~m}

\text{A proton moving with a velocity $\overrightarrow{\boldsymbol{v}}=3.80 \times 10^6 \mathrm{~m} / \mathrm{s}\hspace{1mm} \hat{\boldsymbol{i}}$ enters a region $(x \geq 0)$ containing }

\text{a uniform electric field $\overrightarrow{\boldsymbol{E}}=-5.60 \times 10^4 \mathrm{~N} / \mathrm{C} \hspace{1mm}\hat{\boldsymbol{i}}$. How far will the proton travel in this region }

\text{before it momentarily stops?}

\text{Two identical conducting spheres $A$ and $B$ carry charge $Q_A=+2 Q$ and $Q_B=-3 Q$. They }

\text{are separated by a distance much larger than their diameters. The magnitude of the initial }

\text{electrostatic force between spheres A and B is F. A third, identical uncharged conducting }

\text{sphere $\mathrm{C}$ is first touched to $\mathrm{A}$, then to $\mathrm{B}$, and finally removed.}

\text{As a result, the magnitude of the electrostatic force between A and B after touching is:}

\text{A) $F / 6$}

\text{B) $F / 4$}

\text{C) $\mathrm{F} / 3$}

\text{D) 3 F}

\text{E) 2 F}

\text{Two identical conducting spheres $A$ and $B$ carry charge $Q_A=+2 Q$ and $Q_B=-3 Q$. They }

\text{are separated by a distance much larger than their diameters. The magnitude of the initial }

\text{electrostatic force between spheres A and B is F. A third, identical uncharged conducting }

\text{sphere $\mathrm{C}$ is first touched to $\mathrm{A}$, then to $\mathrm{B}$, and finally removed.}

\text{As a result, the magnitude of the electrostatic force between A and B after touching is:}

\begin{aligned} & F=k\frac{(2 Q)(3 Q)}{d^2}=6k\frac{ Q^2}{d^2} \\ & q_{A}^\prime=\frac{2 Q+0}{2}=Q \\ & q_{B}^\prime=\frac{-3 Q+Q}{2}=-Q \\ & F^\prime=k\frac{ q_{A}^\prime \cdot q_{B}^\prime}{d^2}=k\frac{ QQ}{d^2}=k\frac{ Q^2}{d^2}=\frac{F}{6} \end{aligned}

\text{An electric dipole of dipole moment $|\vec{p}|=2.0 \times 10^{-8} \mathrm{C} . \mathrm{m}$ is initially placed in an electric }

\text{field of magnitude $1.0 \times 10^2 \mathrm{~N} / \mathrm{C}$ in a direction perpendicular to the field. If the dipole is rotated }

\text{to align it in the same direction as the field, find the work done by the field to rotate the dipole.}

\text{A) $+2.0 \hspace{1mm}\mu \mathrm{J}$}

\text{B) $-2.0 \hspace{1mm}\mu \mathrm{J}$}

\text{C) $+4.0\hspace{1mm} \mu \mathrm{J}$}

\text{D) $-4.0 \hspace{1mm}\mu \mathrm{J}$}

\text{E) $+1.0 \hspace{1mm}\mu \mathrm{J}$}

\text{An electric dipole of dipole moment $|\vec{p}|=2.0 \times 10^{-8} \mathrm{C} . \mathrm{m}$ is initially placed in an electric }

\text{field of magnitude $1.0 \times 10^2 \mathrm{~N} / \mathrm{C}$ in a direction perpendicular to the field. If the dipole is rotated }

\text{to align it in the same direction as the field, find the work done by the field to rotate the dipole.}

W=-\Delta U=U_i-U_f ; U_i=0 ; U_f=-p E

W=-U_f=p E=2 \times 10^{-8} \times 1.0 \times 10^2=2 \times 10^{-6} \mathrm{~J}=+2 \mu \mathrm{J}

\vec{E}

\vec{p}

\text{Two charges $\mathrm{q}_1=+6.00 \hspace{1mm}\mu \mathrm{C}$ and $\mathrm{q}_2=-12.0\hspace{1mm} \mu \mathrm{C}$ are placed at $(-2.00 \mathrm{~cm}, 0)$ and $(4.00$ $\mathrm{cm}, 0)$,}

\text{respectively. If a third unknown charge $\mathrm{q}_3$ is to be located such that the net force on it from }

\text{charges $\mathrm{q}_1$ and $\mathrm{q}_2$ is zero, what must be the coordinates of $\mathrm{q}_3$ ?}

\cdot

\cdot

\cdot

q_1=+6

q_3

q_2=-12

4

-2

x

\text{A) $(-16.5 \mathrm{~cm}, 0)$}

\text{C) $(2.49 \mathrm{~cm}, 0)$}

\text{B) $(-14.5 \mathrm{~cm}, 0)$}

\text{D) $(0,0)$}

\text{E) $(-6.50 \mathrm{~cm}, 0)$}

\text{respectively. If a third unknown charge $\mathrm{q}_3$ is to be located such that the net force on it from }

\text{charges $\mathrm{q}_1$ and $\mathrm{q}_2$ is zero, what must be the coordinates of $\mathrm{q}_3$ ?}

\cdot

\cdot

\cdot

q_1=+6

q_3

q_2=-12

4

-2

x

\begin{aligned} & \mathrm{F}_{31}=\mathrm{F}_{32} \\ & k\frac{\mathrm{q}_1 \mathrm{q}_3}{(\mathrm{x}+2)^2}=k\frac{ \mathrm{q}_2 \mathrm{q}_3}{(x-4)^2} \\ & \frac{\mathrm{q}_1 \mathrm{q}_3}{(\mathrm{x}+2)^2}=\frac{\mathrm{q}_2 \mathrm{q}_3}{(x-4)^2} \\ & \frac{6 \times 10^{-6}}{(\mathrm{x}+2)^2}=\frac{12 \times 10^{-6}}{(\mathrm{x}-4)^2} \Rightarrow \frac{1}{(\mathrm{x}+2)^2}=\frac{2}{(\mathrm{x}-4)^2} \end{aligned}

2 (x+2)^2=(x-4)^2\Rightarrow \pm\sqrt{2}(x+2)=x-4

\Rightarrow x=-\frac{\pm2\sqrt{2}+4}{\pm\sqrt{2}-1}

\text{Only $x=-\frac{2\sqrt{2}+4}{\sqrt{2}-1}=-16.48$ is accepted because negative}

\text{(the other one does not fulfill the stability condition )}

\text{We can have equilibrium only if $q_3$ is at the left}

\text{Two charges $\mathrm{q}_1=+6.00 \hspace{1mm}\mu \mathrm{C}$ and $\mathrm{q}_2=-12.0\hspace{1mm} \mu \mathrm{C}$ are placed at $(-2.00 \mathrm{~cm}, 0)$ and $(4.00$ $\mathrm{cm}, 0)$,}

\text{(x represents here the position)}

\text{An electric dipole is placed in a uniform electric field $\vec{E}=(4000 \hat{i}) N / C$. What is the change }\\

\text{in dipole's potential energy if the initial and the final electric dipole moments $\vec{p}_i$ and $\vec{p}_\text{f}$ }

\\ \begin{aligned} & \vec{p}_i=\left(3.72 \times 10^{-30} \hat{i}+4.96 \times 10^{-30} \hat{j}\right) \text { C.m } \\ & \vec{p}_\text{f}=\left(6.20 \times 10^{-30} \hat{i}\right) \mathrm{C} . \mathrm{m} \end{aligned}

\text{respectively, are given by}

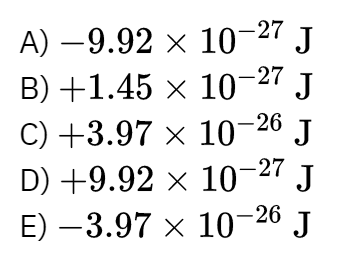
\text{An electric dipole is placed in a uniform electric field $\vec{E}=(4000 \hat{i}) N / C$. What is the change }\\

\text{in dipole's potential energy if the initial and the final electric dipole moments $\vec{p}_i$ and $\vec{p}_\text{f}$ }

\\ \begin{aligned} & \vec{p}_i=\left(3.72 \times 10^{-30} \hat{i}+4.96 \times 10^{-30} \hat{j}\right) \text { C.m } \\ & \vec{p}_\text{f}=\left(6.20 \times 10^{-30} \hat{i}\right) \mathrm{C} . \mathrm{m} \end{aligned}

\text{respectively, are given by}

\begin{aligned} U & =-\vec{P} \cdot \vec{E} \\ \Delta U & =U_\text{f}-U_i=\left(-\vec{P}_\text{f} \cdot \vec{E} \right)-\left(-\vec{P}_i \cdot \vec{E}\right) \\ & =\left[3.72 \times 10^{-30} \times 4000\right]+\left[-6.2 \times 10^{-30} \times 4000\right] \\ & =+1.488 \times 10^{-26}-2.48 \times 10^{-26}=-9.92 \times 10^{-27} J \end{aligned}

\text{An electron is shot (ejected) at an initial speed of $3.0 \times 10^4 \mathrm{~m} / \mathrm{s}$ at an angle of $45^{\circ}$ relative }

\text{to the positive x-axis, as shown in FIGURE 3. At time $t=0$, the electron enters a region of }

\text{uniform electric field $\overrightarrow{\mathbf{E}}=2.0 \times 10^{-6} \hat{\mathbf{j}}(\mathrm{N} / \mathrm{C})$. Find the velocity of the electron along y-axis at}

\text{$t=1.0 \mathrm{~s}$. Ignore gravity.}

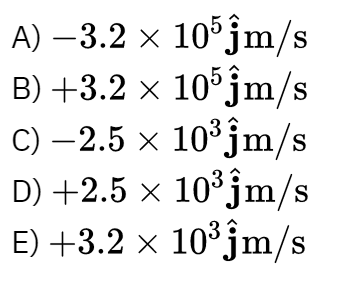
45^0

\vec{E}

x

y

\cdot

e

\vec{v}

-

\text{An electron is shot (ejected) at an initial speed of $3.0 \times 10^4 \mathrm{~m} / \mathrm{s}$ at an angle of $45^{\circ}$ relative }

\text{to the positive x-axis, as shown in FIGURE 3. At time $t=0$, the electron enters a region of }

\text{uniform electric field $\overrightarrow{\mathbf{E}}=2.0 \times 10^{-6} \hat{\mathbf{j}}(\mathrm{N} / \mathrm{C})$. Find the velocity of the electron along y-axis at}

\text{$t=1.0 \mathrm{~s}$. Ignore gravity.}

45^0

\vec{E}

x

y

\cdot

e

\begin{aligned} & F_e=m a \Rightarrow q E=m a \Rightarrow a=\frac{q E}{m} \\ & \therefore a=\frac{-1.6 \times 10^{-19} \times 2.0 \times 10^{-6}}{9.11 \times 10^{-31}}=-3.5 \times 10^5 \mathrm{~m} / \mathrm{s}^2 \\ & \Rightarrow \vec{a}=-3.5 \times 10^5 \hat{j}\left(\mathrm{~m} / \mathrm{s}^2\right) \\ & v_y=v_{\text {y }}^0+a t \\ & =\left(3.0 \times 10^4\right)\textcolor{red}{\sin45^0}-\left(3.5 \times 10^5 \times 1.0\right)=-3.3 \times 10^5 \mathrm{~m} / \mathrm{s} \\ & \Rightarrow \vec{v}_y=-3.3 \times 10^5 \hat{j} \mathrm{~m} / \mathrm{s} \end{aligned}

\text{The force is opposit to $\vec{E}$}

\vec{v}

\vec{a} \text{ is downward}

-

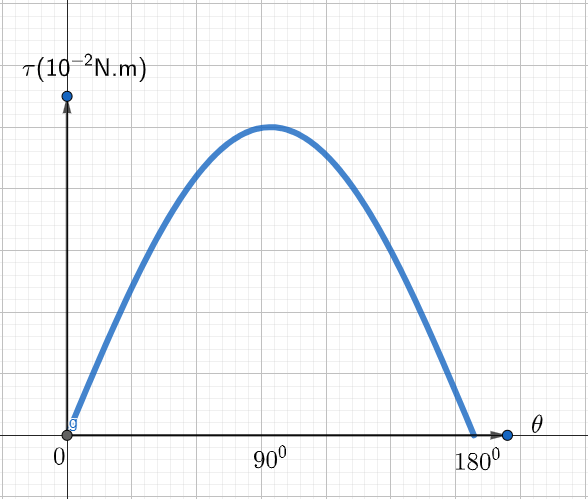
\text{A certain electric dipole is placed in a uniform electric field $\vec{E}$ of magnitude $10 \mathrm{~N} / \mathrm{C}$. The}

\text{magnitude of torque on the dipole plotted as a function of the angle between $\vec{E}$ and the }

\text{dipole moment $\vec{p}$ is shown in the figure. How much work is needed by an external agent to }

\text{turn the electric dipole from $30^{\circ}$ to $60^{\circ}$ with respect to $\vec{E}$ field?}

\text{A) $+1.83 \times 10^{-1} \mathrm{~J}$}

\text{B) $-1.83 \times 10^{-1} \mathrm{~J}$}

\text{C) $+2.66 \times 10^{-1} \mathrm{~J}$}

\text{D) $-2.66 \times 10^{-1} \mathrm{~J}$}

\text{E) $+9.20 \times 10^{-2} \mathrm{~J}$}

\begin{aligned} & W_a=\Delta U=U_f-U_i \\ &=-p E \cos \theta_f-\left(-p E \cos \theta_i\right) \\ &=p E\left(\cos \theta_i-\cos \theta_f\right) \\ & \tau=p E \sin \theta \\ & \text { at } \theta=90^{\circ} \quad \tau=p E=50 \times 10^{-2} \mathrm{~N}. m \text { (from the figure) } \\ & \Rightarrow W_a=50 \times 10^{-2}\left(\cos 30^{\circ}-\cos 60^{\circ}\right) \\ & W_a=0.18 \mathrm{~J}=+1.8 \times 10^{-1} \mathrm{~J} \end{aligned}

\text{A certain electric dipole is placed in a uniform electric field $\vec{E}$ of magnitude $10 \mathrm{~N} / \mathrm{C}$. The}

\text{magnitude of torque on the dipole plotted as a function of the angle between $\vec{E}$ and the }

\text{dipole moment $\vec{p}$ is shown in the figure. How much work is needed by an external agent to }

\text{turn the electric dipole from $30^{\circ}$ to $60^{\circ}$ with respect to $\vec{E}$ field?}

-

-

20

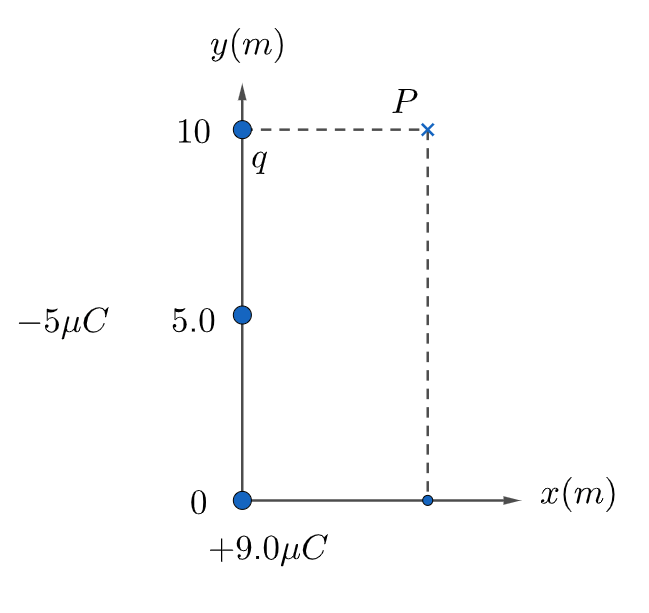
\text{As shown in Figure 3 three charges $+9.0 \mu \mathrm{C},-5.0 \mu \mathrm{C}$ and q , are placed along $y$ axis. If the }

\text{net electric field $E$ at the point $P$ due to these charges points in the $y$ direction, determine }

\text{the charge q?}

5

\text{As shown in Figure 3 three charges $+9.0 \mu \mathrm{C},-5.0 \mu \mathrm{C}$ and q , are placed along $y$ axis. If the }

\text{net electric field $E$ at the point $P$ due to these charges points in the $y$ direction, determine }

\text{the charge q?}

\vec{E}=\vec{E}_1+\vec{E}_2+\vec{E}_3

\text{The projection on x-axis gives:}

0=k\frac{|q_1|}{r_1^2}\cos\theta_1-k\frac{|q_2|}{r_2^2}\cos\theta_2+k\frac{q_3}{r_3^2}

\theta_1

\theta_2

\text{from the rectangle triangles, we can see that:}

\cos\theta_1=\frac{1}{\sqrt{5}}

\cos\theta_2=\frac{1}{\sqrt{2}}

r_1=5\sqrt{5},r_2=5\sqrt{2}, r_3=5

0=\frac{9}{125}\frac{1}{\sqrt{5}}-\frac{5}{50}\frac{1}{\sqrt{2}}+\frac{q_3}{25}

q=\frac{5}{2}\frac{1}{\sqrt{2}}-\frac{9}{5}\frac{1}{\sqrt{5}}=0.96 \mu C

r_1

r_2

r_3

\text{FIGURE 3 shows a horizontal electric field of magnitude $2.00 \times 10^5 \mathrm{~N} / \mathrm{C}$ that causes }

\text{a small ball of mass 2.00 g and charge 25.0 nC attached to an insulating massless string to}

\text{hang in air. Ignoring air friction, find the angle $\theta$.}

\text{A) $14.3^{\circ}$}

\text{B) $10.9^{\circ}$}

\text{C) $18.2^{\circ}$}

\text{E) $22.5^{\circ}$}

\text{D) $19.1^{\circ}$}

\text{E) $22.5^{\circ}$}

+

\vec{E}

\theta

25 \text{ nC}

2.0 \text{ g}

\text{Figure 3}

\text{FIGURE 3 shows a horizontal electric field of magnitude $2.00 \times 10^5 \mathrm{~N} / \mathrm{C}$ that causes }

\text{a small ball of mass 2.00 g and charge 25.0 nC attached to an insulating massless string to}

\text{hang in air. Ignoring air friction, find the angle $\theta$.}

\text{A) $14.3^{\circ}$}

\text{B) $10.9^{\circ}$}

\text{C) $18.2^{\circ}$}

\text{E) $22.5^{\circ}$}

\text{D) $19.1^{\circ}$}

\text{E) $22.5^{\circ}$}

+

\vec{E}

\theta

25 \text{ nC}

2.0 \text{ g}

\text{Figure 3}

\vec{T}

\vec{F}

m\vec{g}

\vec{F}+m\vec{g}+\vec{T}=0

\text{Projection on y-axis:}

T\cos\theta=mg

\text{Projection on x-axis:}

T\sin\theta=qE

\text{We deduce that}

\tan\theta=\frac{q E}{mg}=\frac{25\times 10^{-9}\times 2\times10^5}{2 \times 10^{-3}\times 9.8}=2.55 \times 10^{-1}

\theta=14.3^0

\text{A uniform electric field has a magnitude of $2.0 \times 10^4 \mathrm{~N} / \mathrm{C}$ and points to the right. An electron }

\text{is released from rest in this electric field. How far and in what direction will the electron travel }

\text{in two nanoseconds after its release?}

\text{A uniform electric field has a magnitude of $2.0 \times 10^4 \mathrm{~N} / \mathrm{C}$ and points to the right. An electron }

\text{is released from rest in this electric field. How far and in what direction will the electron travel }

\text{in two nanoseconds after its release?}

\begin{aligned} \mathrm{x} & =v_{\mathrm{i}} \mathrm{t}+\frac{1}{2} \mathrm{at}^2 \\ & =\left(\frac{1}{2}\right)\left(\frac{\mathrm{eE}}{\mathrm{m}}\right) \mathrm{t}^2 \\ & =\frac{1.6 \times 10^{-19} \times 2 \times 10^4 \times 4 \times 10^{-18}}{2 \times 9.11 \times 10^{-31}} \\ & =0.70 \times 10^{-2}=7.0 \mathrm{~mm} \end{aligned}

\text{ Consider three different electric dipoles placed in the same uniform electric field $\mathbf{E}$, as shown }

\text{in FIGURE 4, where $\theta=60^{\circ}$.}

\text{Which of these dipoles has (or have) the LOWEST electric potential energy?}

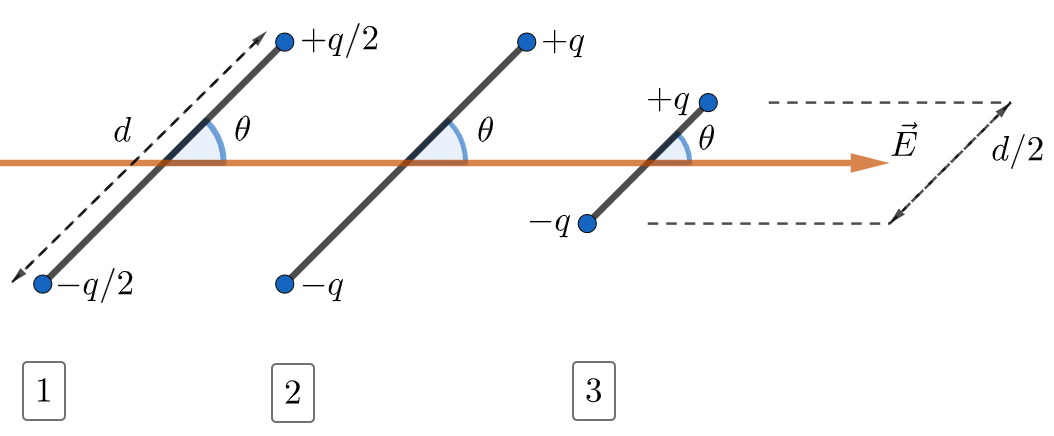
\text{ Consider three different electric dipoles placed in the same uniform electric field $\mathbf{E}$, as shown }

\text{in FIGURE 4, where $\theta=60^{\circ}$.}

\text{Which of these dipoles has (or have) the LOWEST electric potential energy?}

\begin{aligned} & \mathrm{U}=-\overrightarrow{\mathrm{p}} \cdot \overrightarrow{\mathrm{E}} \\ & \mathrm{U}_1=-\frac{\mathrm{qd}}{2} \cdot E \cdot \frac{1}{2}=-\frac{\mathrm{qdE}}{4} \\ & \mathrm{U}_2=-\mathrm{qd} \cdot \mathrm{E} \cdot \frac{1}{2}=-\frac{\mathrm{qdE}}{2} \\ & \mathrm{U}_3=-\mathrm{q} \cdot \frac{\mathrm{d}}{2} \cdot \mathrm{E} \cdot \frac{1}{2}=-\frac{\mathrm{qdE}}{4} \end{aligned}