y_m^{\prime}=\left|2 y_m \cos \frac{1}{2} \phi\right| \quad \text { (amplitude). }

y^{\prime}(x, t)=\left[2 y_m \sin k x\right] \cos \omega t .

y^{\prime}(x, t)=\left[2 y_m \cos \frac{1}{2} \phi\right] \sin \left(k x-\omega t+\frac{1}{2} \phi\right) \text {. }

P_{\mathrm{avg}}=\frac{1}{2} \mu \nu \omega^2 y_m^2

v=\sqrt{\frac{\tau}{\mu}}

v=\frac{\omega}{k}=\frac{\lambda}{T}=\lambda f

k=\frac{2 \pi}{\lambda}

\frac{\omega}{2 \pi}=f=\frac{1}{T}

y(x, t)=y_m \sin (k x-\omega t)

\text{propagating wave}

\text{wave on a stretched string}

\text{wave interference}

\text{wave speed doesn't depend on the frequency}

\text{standing wave}

\text{Resonance}

\text{stretched string with fixed ends}

f=\frac{v}{\lambda}=n \frac{v}{2 L}, \quad \text { for } n=1,2,3, \ldots

\text{two waves shifted by $\Delta x$ have a differnce of phase}

\Delta \phi=k\Delta x=2\pi \frac{\Delta x}{\lambda}

\text{$n=1$ is the fundamental}

\text{The displacement of a string carrying a traveling sinusoidal wave is given by:}\\ y(x, t)=y_m \sin (k x-\omega t+\varphi) .

\text{At time $t=0$ the point at $x=0$ has a displacement of zero and is moving in the positive}

\text{ $y$ direction. Find the value of the phase constant $\varphi$.}

\begin{aligned} &\text{A) 180 degrees} \\ &\text{B) 90 degrees} \\ &\text{C) 135 degrees} \\ &\text{D) 0 degrees} \\ &\text{E) 270 degrees} \end{aligned}

\text{The displacement of a string carrying a traveling sinusoidal wave is given by:}\\ y(x, t)=y_m \sin (k x-\omega t+\varphi) .

\text{At time $t=0$ the point at $x=0$ has a displacement of zero and is moving in the positive}

\text{ $y$ direction. Find the value of the phase constant $\varphi$.}

\displaystyle y=y_m \sin\phi=0\Rightarrow \sin \phi=0

\text{at $x=0$, $t=0$, we have }

\Rightarrow \phi = \begin{cases} 0 \\ \pi \end{cases}

\displaystyle u(0,0)=-\omega y_m \cos\phi>0 \Rightarrow \cos \phi<0

\text{We deduce that: $\phi=\pi$}

\text{Reminder:}

\text{The equation } \sin\theta=a

\text{has two solutions in } [0, 2\pi]:

\theta=\theta_0

\theta=\pi-\theta_0

\text{where } \theta_0=\sin^{-1}a

\text{Your calculator gives only one of them}

\text{(We use the transverse speed to find which angle is correct)}

\text{(moving upward, $\Rightarrow u>0$)}

\text{A transverse sinusoidal wave is travelling on a stretched string. The maximum transverse }

\text{speed of a particle on the string is $24.0 \mathrm{~m} / \mathrm{s}$.}

\text{The frequency of oscillations of a particle }

\text{in the string is $120 \mathrm{~Hz}$. What is the amplitude of the wave?}

\text{A) $31.8 \mathrm{~mm}$}

\text{B) $25.1 \mathrm{~mm}$}

\text{C) $12.0 \mathrm{~mm}$}

\text{D) $43.3 \mathrm{~mm}$}

\text{E) $53.2 \mathrm{~mm}$}

\text{A transverse sinusoidal wave is travelling on a stretched string. The maximum transverse }

\text{speed of a particle on the string is $24.0 \mathrm{~m} / \mathrm{s}$.}

\text{The frequency of oscillations of a particle }

\text{in the string is $120 \mathrm{~Hz}$. What is the amplitude of the wave?}

u_m=\omega y_m \Rightarrow y_m=\frac{u_m}{\omega}=\frac{u_m}{2\pi f}=\frac{24}{2 \pi\times 120}=0.0318\hspace{1mm} m

\text{The maximum transverse speed is}

\text{Figure 1 shows a snapshot graph of a wave traveling to the right along a string at 25 $\mathrm{m} / \mathrm{s}$.}

\text{At this instant, what are the velocities of points A, B , and C on the string, respectively?}

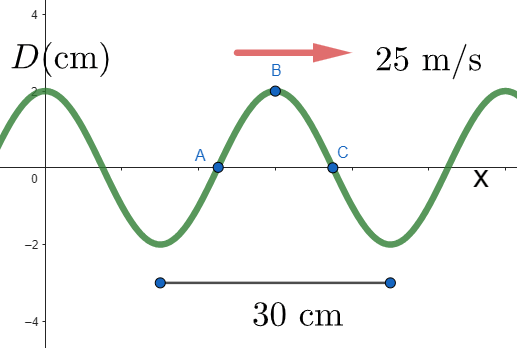
\text{A) $-11 \mathrm{~m} / \mathrm{s}, 0,+11 \mathrm{~m} / \mathrm{s}$}

\text{B) $-11 \mathrm{~m} / \mathrm{s}, 0,-11 \mathrm{~m} / \mathrm{s}$}

\text{C) $0,-11 \mathrm{~m} / \mathrm{s}, 0$}

\text{D) $0,+11 \mathrm{~m} / \mathrm{s},-11 \mathrm{~m} / \mathrm{s}$}

\text{E) $-19 \mathrm{~m} / \mathrm{s}, 0,+19 \mathrm{~m} / \mathrm{s}$}

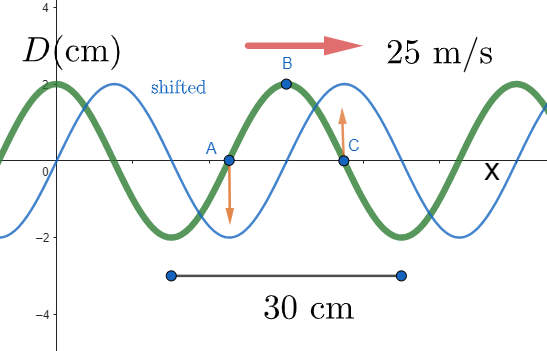
\text{We shift the wave to the \textcolor{red}{right}}

\text{(because it is a right moving wave)}

\text{We check in which direction each point moves}

\text{A: down, C: Up}

\left|u_{\max }\right|=\omega y_m=2 \pi f y_m

f=\frac{v}{\lambda}=\frac{25}{0.3}=83.33 \mathrm{~m} / \mathrm{s}

\left|u_{\max }\right|=2 \pi \times 83.33 \times 2 \times 10^{-2}=10.47 \mathrm{~m} / \mathrm{s}\approx11 \mathrm{~m} / \mathrm{s}

\text{Figure 1 shows a snapshot graph of a wave traveling to the right along a string at 25 $\mathrm{m} / \mathrm{s}$.}

\text{At this instant, what are the velocities of points A, B , and C on the string, respectively?}

\text{At B, the transverse speed=0}

\text{At A and C, the transverse speed is maximum}

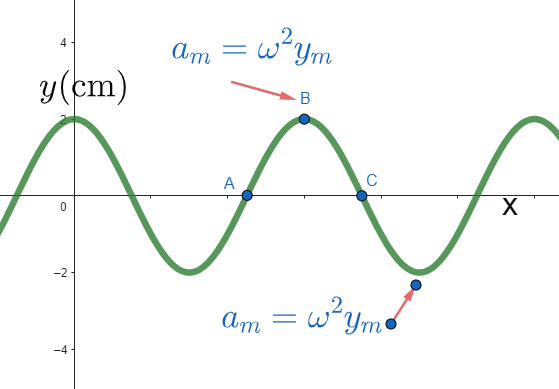
\text{The displacement of a particle moving in simple harmonic motion is given by the equation:}

\text{ $y(t)=2.0 \cos (kx-6.0 t)$, where $y$ is in meters and $t$ is in seconds. }

\text{What is the maximum acceleration of the particle and where does it occur?}

y(t)=2 \cos(kx-6.0 t)

\omega=6 \text{ rad/s}

a(t)=-\omega^2 y(t)

a(t) \text{ will be maximum for } y(t)=-y_m

a_m=\omega^2 y_m=6^2\times 2=72 \text{ $m/s^2$}

\text{ for $y(t)$ minimum}

\text{The displacement of a particle moving in simple harmonic motion is given by the equation:}

\text{ $y(t)=2.0 \cos (kx-6.0 t)$, where $y$ is in meters and $t$ is in seconds. }

\text{What is the maximum acceleration of the particle and where does it occur?}

\text{A stretched string of mass $2.0 \mathrm{~g}$ and length $10 \mathrm{~cm}$, carries a wave having the following }

\text{displacement wave: $y(x, t)=0.05 \sin (2 \pi x-400 \pi t)$, where $x$ and $y$ are in meters }

\text{and $t$ is in seconds. What is the tension in the string?}

\begin{aligned} v=\sqrt{\frac{\tau}{\mu}} \Rightarrow \tau & =v^2 \mu=\left(\frac{\omega}{k}\right)^2 \mu=\left(\frac{\omega}{k}\right)^2 \frac{m}{l} \\ \tau & =\left(\frac{400 \pi}{2 \pi}\right)^2 \frac{2 \times 10^{-3}}{10 \times 10^{-2}}=800 \mathrm{~N} \end{aligned}

\text{A stretched string of mass $2.0 \mathrm{~g}$ and length $10 \mathrm{~cm}$, carries a wave having the following }

\text{displacement wave: $y(x, t)=0.05 \sin (2 \pi x-400 \pi t)$, where $x$ and $y$ are in meters }

\text{and $t$ is in seconds. What is the tension in the string?}

\text{FIGURE 1 shows a graph that represents a transverse wave on a string. The wave is moving}

\text{in the $+x$ direction with a speed of $0.15 \mathrm{~m} / \mathrm{s}$. Using the information contained in the graph,}

\text{write the expression for the wave}

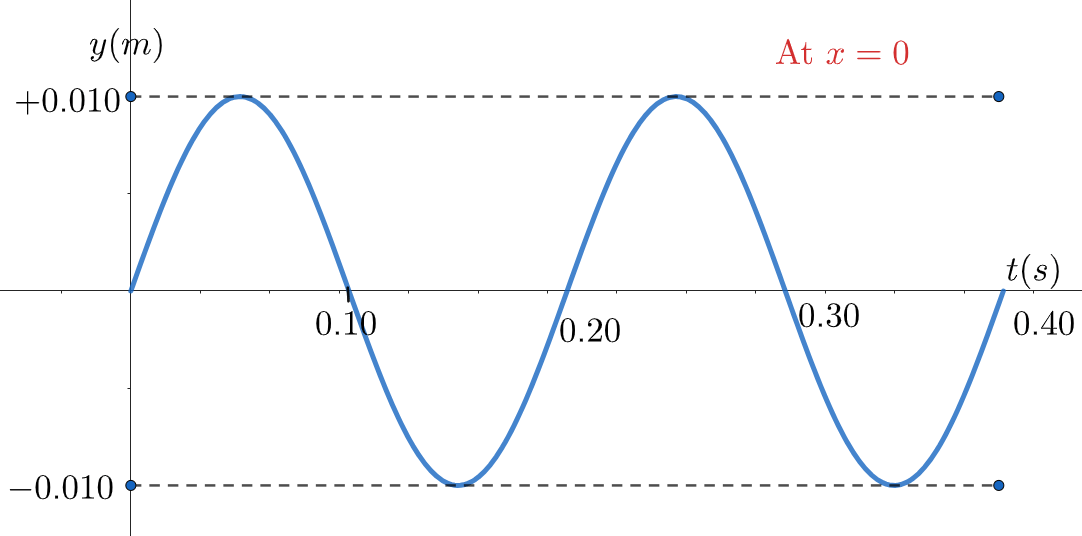
\text{A) $y=0.01 \sin (209 x-31.4 t)$}

\text{B) $y=0.01 \sin (209 x+31.4 t)$}

\text{C) $y=0.04 \sin (209 x-6.28 t)$}

\text{D) $y=0.01 \sin (0.942 x-31.4 t)$}

\text{E) $y=0.01 \sin (0.942 x+31.4 t)$}

\text{FIGURE 1 shows a graph that represents a transverse wave on a string. The wave is moving}

\text{in the $+x$ direction with a speed of $0.15 \mathrm{~m} / \mathrm{s}$. Using the information contained in the graph,}

\text{write the expression for the wave}

\begin{aligned} & \omega=\frac{2 \pi}{T}=\frac{2 \pi}{0.2}=10 \pi=31.4 \text{ rad/s}\\ &\\ & \mathrm{~k}=\frac{\omega}{v}=\frac{10 \pi}{0.15}=\frac{200}{3} \pi=209 \text{ rad/m} \end{aligned}

y_m=0.01 \text{ m}

\mathrm{T}=0.2\text{ s}

\text{right moving wave, so: $ y=0.01 \sin (209 x-31.4 t)$ }

\text{The amplitude is:}

\text{Graph: displacement vs time}

\text{Two pieces of string, each of length $L=1.5 \mathrm{~m}$, are joined together end to end, to make }

\text{a $3.0 \mathrm{~m}$ long combined string. The first piece of string has mass per unit length $\mu_1=100$ $\mathrm{g} / \mathrm{m}$, }

\text{the second piece has mass per unit length $\mu_2=6.0 \mu_1$.}

\text{travelling wave to travel the entire $3.0 \mathrm{~m}$ length of the string?}

\text{If the combined string is under tension $\tau=5.0 \mathrm{~N}$, how much time does it take a transverse }

\text{A) $0.73 \mathrm{~s}$}

\text{B) $1.1 \mathrm{~s}$}

\text{C) $1.7 \mathrm{~s}$}

\text{D) $1.9 \mathrm{~s}$}

\text{E) $2.8 \mathrm{~s}$}

\text{Two pieces of string, each of length $L=1.5 \mathrm{~m}$, are joined together end to end, to make }

\text{a $3.0 \mathrm{~m}$ long combined string. The first piece of string has mass per unit length $\mu_1=100$ $\mathrm{g} / \mathrm{m}$, }

\text{the second piece has mass per unit length $\mu_2=6.0 \mu_1$.}

\text{travelling wave to travel the entire $3.0 \mathrm{~m}$ length of the string?}

\text{If the combined string is under tension $\tau=5.0 \mathrm{~N}$, how much time does it take a transverse }

\displaystyle t_{\text {Tot }}=L\left(\frac{1}{v_1}+\frac{1}{v_2}\right)=L\left(\sqrt{\frac{\mu_1}{\tau}}+\sqrt{\frac{\mu_2}{\tau}}\right)=1.5\left[\sqrt{\frac{0.1}{5}}+\sqrt{\frac{0.6}{5}}\right]=0.731 \mathrm{~s}

t_\text{Tot}=t_1+t_2

\text{The cords in the three configurations are the same. All the objects have the same mass.}

\text{In which configuration, the wave speed in the cord is maximum?}

\text{The cords in the three configurations are the same. All the objects have the same mass.}

\text{In which configuration, the wave speed in the cord is maximum?}

\tau_1

\tau_2

\tau_3

\tau_1=mg

\tau_2=mg

\tau_3=2mg

\tau_2

\text{The highest speed is in configuration 3}

\text{The speeds in configurations 1 and 2 are tie}

(\text{The tension in the string is constant})

(\text{we neglect the mass of the hanging string})

mg

mg

mg

2mg

\text{A $0.550 \mathrm{~m}$ long string fixed at both ends is vibrating in its fundamental mode. }

\text{The maximum transverse acceleration of a point at the middle of the string is $8.40 \times 10^3$ $\mathrm{m} / \mathrm{s}^2$ }

\text{and the maximum transverse velocity is $3.80 \mathrm{~m} / \mathrm{s}$.}

\text{What is the wave speed of the transverse waves traveling on this string? }

\begin{aligned} & \frac{a_{\max }}{u_{\max }}=\frac{y_m^{\prime} \omega^2}{y_m^{\prime} \omega}=\omega=\frac{8.4 \times 10^3}{3.8}=2210.5 \mathrm{rad} / \mathrm{s} \\ & \lambda=2 L=2 \times 0.55=1.1 \mathrm{~m} \\ & v=\frac{\omega}{k}=\frac{\lambda \omega}{2 \pi}=\frac{1.1 \times 2210.5}{2 \pi}=386.99 \mathrm{~m} / \mathrm{s} \end{aligned}

\text{A $0.550 \mathrm{~m}$ long string fixed at both ends is vibrating in its fundamental mode. }

\text{The maximum transverse acceleration of a point at the middle of the string is $8.40 \times 10^3$ $\mathrm{m} / \mathrm{s}^2$ }

\text{and the maximum transverse velocity is $3.80 \mathrm{~m} / \mathrm{s}$.}

\text{What is the wave speed of the transverse waves traveling on this string? }

\text{(because it is the fundamental)}

y^{\prime}(x, t)=\left[2 y_m \sin k x\right] \cos \omega t .

\text{(standing wave equation)}

u(x, t)=-\left[2 y_m \omega \sin k x\right] \sin\omega t .

a(x, t)=-\left[2 y_m \omega^2 \sin k x\right] \cos\omega t .

\text{Two sinusoidal waves, identical except for phase, travel in the same direction along }

\text{a stretched string, producing a resultant wave $y(x, t)=0.097 \sin (15 x-2.4 t+0.78)$,}

\text{where $x$ is in meters and $t$ is in seconds. What is the amplitude of the interfering waves? }

\text{A) $0.068 \mathrm{~m}$}

\text{B) $0.052 \mathrm{~m}$}

\text{C) $0.097 \mathrm{~m}$}

\text{D) $0.035 \mathrm{~m}$}

\text{E) $0.044 \mathrm{~m}$}

\text{Two sinusoidal waves, identical except for phase, travel in the same direction along }

\text{a stretched string, producing a resultant wave $y(x, t)=0.097 \sin (15 x-2.4 t+0.78)$,}

\text{where $x$ is in meters and $t$ is in seconds. What is the amplitude of the interfering waves? }

y^{\prime}(x, t)=\left[2 y_m \cos \frac{1}{2} \phi\right] \sin \left(k x-\omega t+\frac{1}{2} \phi\right) \text {. }

\text{We can see that: }\frac{\phi}{2}=0.78 \text{ rad}

2 y_m |\cos \frac{1}{2} \phi|=0.097 \Rightarrow y_m=\displaystyle \frac{0.097}{2 |\cos \frac{1}{2} \phi|}=\frac{0.097}{2 |\cos 0.78|}=0.068 \text{ m}

\text{(resultant wave)}

\begin{gathered} \text{A)1.83 m }\\ \text{B)1.22 m } \\ \text{C)1.12 m }\\ \text{D)2.86 m }\\ \text{E)2.12 m } \end{gathered}

\begin{aligned} &\text{A light string is fixed between two supports with two successive standing-wave frequencies}\\ &\text{occur at 525 Hz and 630 Hz. There are other standing-wave frequencies lower than 525 Hz}\\ &\text{and higher than 630 Hz. If the speed of transverse waves on the string is 384 m/ s, then find }\\ &\text{the length of the string?} \end{aligned}

\begin{aligned} & f_1=630-525=105 \mathrm{~Hz} \\ & f_1=\frac{ v}{2 L}=\frac{384}{2 L}=105 \mathrm{~Hz} \\ & \Rightarrow L=1.83 \mathrm{~m} \end{aligned}

\text{The difference between successive frequencies gives the fundamental}

\begin{aligned} &\text{A light string is fixed between two supports with two successive standing-wave frequencies}\\ &\text{occur at 525 Hz and 630 Hz. There are other standing-wave frequencies lower than 525 Hz}\\ &\text{and higher than 630 Hz. If the speed of transverse waves on the string is 384 m/ s, then find }\\ &\text{the length of the string?} \end{aligned}

\text{A string oscillates in a third -harmonic standing wave pattern. The amplitude at a point }

\text{$30 \mathrm{~cm}$ from one end of the string is half the maximum amplitude. How long is the string?}

\text{A string oscillates in a third -harmonic standing wave pattern. The amplitude at a point }

\text{$30 \mathrm{~cm}$ from one end of the string is half the maximum amplitude. How long is the string?}

L=\frac{3 \lambda}{2} \Rightarrow k=\frac{2 \pi}{\lambda}=2 \pi \times \frac{3}{2 L}=\frac{3 \pi}{L}

\operatorname{Amplitude}\text{ at }(x=0.3 m) ; y'_m=2 y_m \operatorname{sin}k x=2 y_m \sin \left(\frac{3 \pi}{L} \times 0.3\right)=y_m

1=2 \sin \left(\frac{0.9 \pi}{L}\right)

L=\frac{0.9 \pi}{\sin ^{-1}\left(\frac{1}{2}\right)}=\frac{0.9 \pi}{30^{\circ}}=\frac{0.9 \pi}{\pi / 6}=6 \times 0.9=5.4 \mathrm{~m}

\text{(maximum amplitude is $2y_m$)}

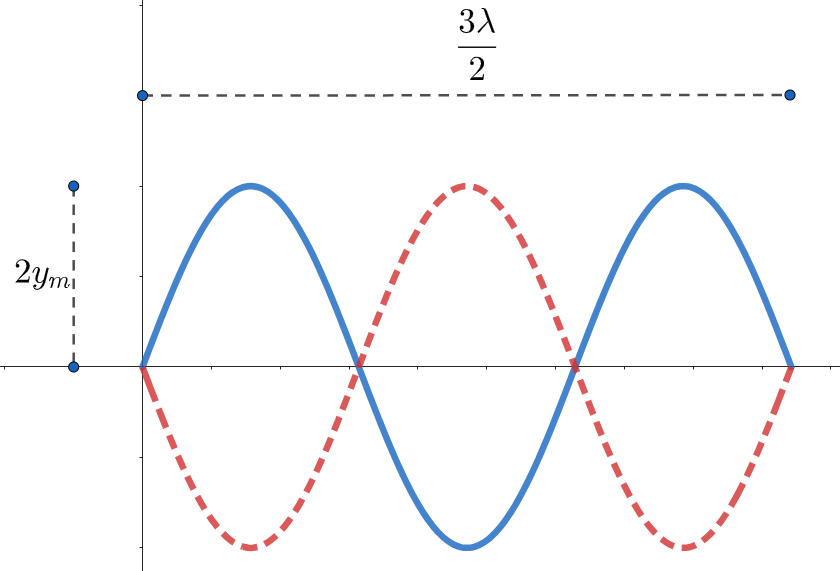
\text{A string oscillates in a third -harmonic standing wave pattern. The amplitude at a point }

\text{$30 \mathrm{~cm}$ from one end of the string is half the maximum amplitude. How long is the string?}

y'_m=2 y_m |\operatorname{sin}k x|=2 y_m \Big|\sin \left(\frac{3 \pi}{L} \times 0.3\right)\Big|=y_m

\frac{1}{2}=\Big| \sin \left(\frac{0.9 \pi}{L}\right)\Big|

L=\frac{0.9 \pi}{\sin ^{-1}\left(\displaystyle\textcolor{red}{\pm}\frac{1}{2}\right)}

\text{The previous solution is actually incomplete.}

\text{The correct way is to do it as follows}

\sin^{-1}(\frac{1}{2})=\frac{\pi}{6}+2\pi n

\sin^{-1}(\frac{1}{2})=\frac{5\pi}{6}+2\pi n

\text{ or }

\text{with $n$ integer}

\text{A string oscillates in a third -harmonic standing wave pattern. The amplitude at a point }

\text{$30 \mathrm{~cm}$ from one end of the string is half the maximum amplitude. How long is the string?}

L=\frac{0.9 \pi}{\sin ^{-1}\left(\displaystyle\pm\frac{1}{2}\right)}

\sin^{-1}(\frac{1}{2})=\frac{\pi}{6}+2\pi n

a)

L=\frac{5.4}{1+12n}

\text{the acceptable $n$ for which $L>(x=0.3)$ are}

n=0,1

\text{So, $L=5.4 $ m or $L=0.42 $ m}

\sin^{-1}(\frac{1}{2})=\frac{5\pi}{6}+2\pi n

L=\frac{5.4}{5+12n}

\text{the acceptable $n$ for which $L>(x=0.3)$ are}

n=0,1

\text{So, $L=1.08 $ m or $L=0.32 $ m}

b)

\text{A string oscillates in a third -harmonic standing wave pattern. The amplitude at a point }

\text{$30 \mathrm{~cm}$ from one end of the string is half the maximum amplitude. How long is the string?}

L=\frac{0.9 \pi}{\sin ^{-1}\left(\displaystyle\pm\frac{1}{2}\right)}

\sin^{-1}(-\frac{1}{2})=-\frac{\pi}{6}+2\pi n

c)

L=\frac{5.4}{-1+12n}

\text{the acceptable $n$ for which $L>(x=0.3)$ are}

n=1

\text{So, $L=0.42 $ m}

\sin^{-1}(-\frac{1}{2})=-\frac{5\pi}{6}+2\pi n

L=\frac{5.4}{-5+12n}

\text{the acceptable $n$ for which $L>(x=0.3)$ are}

n=1,2

\text{So, $L=0.77 $ m}

d)

\cdot

\cdot

\cdot

\cdot

\cdot

\cdot

\text{(as we can see from the figure, there are 6 possible points)}

\text{Strings A and B have identical lengths and linear densities, but string A is under greater tension }

\text{than string B. Figure 1 shows four situations, in which standing wave patterns exist on the two }

\text{strings. In which situation(s) is there the possibility that strings A and B are oscillating at the}

\text{ same resonant frequency? }

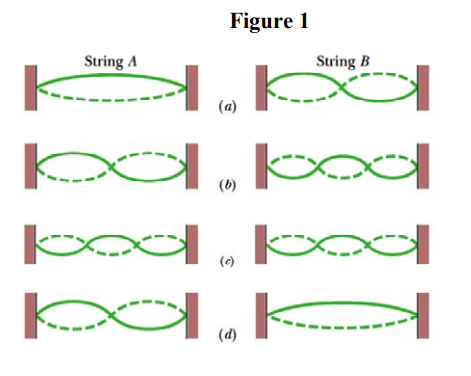
\text{Strings A and B have identical lengths and linear densities, but string A is under greater tension }

\text{than string B. Figure 1 shows four situations, in which standing wave patterns exist on the two }

\text{strings. In which situation(s) is there the possibility that strings A and B are oscillating at the}

\text{ same resonant frequency? }

\begin{aligned} & v=\sqrt{\frac{\tau}{\mu}} \\ & v_A>v_B \\ & f_{n A}=\frac{n_A v_A}{2 L}, f_{n B}=\frac{n_B v_B}{2 L} \\ & \frac{n_A v_A}{2 L}=\frac{n_B v_B}{2 L} \end{aligned}

n_B=\frac{v_A}{v_B} n_A

\Rightarrow

n_B> n_A

\text{because $(v_A>v_B$)}

\Rightarrow

\text{The possible situations are a and b}

\begin{aligned} & P_1=\frac{1}{2} \mu_1 v_1\omega^2 y_m^2 \\ & \mu_2=2 \mu_1 ; v_2=\sqrt{\frac{\tau}{\mu_2}}=\frac{v_1}{\sqrt{2}} \\ & P_2=\frac{1}{2} 2 \mu_1 \frac{v_1}{\sqrt{2}} \omega^2 y_m^2 \\ & P_2=\frac{2}{\sqrt{2}}\left[\frac{1}{2} \mu_1 v_1\omega^2 y_m^2 \right]=\sqrt{2} P_1 \approx 1.4 P_1 \end{aligned}

\text{Standing waves are created in a $160 \mathrm{~cm}$ long string. The string has two adjacent resonances }

\text{at frequencies of $85.0 \mathrm{~Hz}$ and $102 \mathrm{~Hz}$.}

\text{What is the length of each loop at the $85.0 \mathrm{~Hz}$ resonance?}

\text{A) $32.0 \mathrm{~cm}$}

\text{B) $10.4 \mathrm{~cm}$}

\text{C) $68.0 \mathrm{~cm}$}

\text{D) $83.5 \mathrm{~cm}$}

\text{E) $25.7 \mathrm{~cm}$}

\text{Standing waves are created in a $160 \mathrm{~cm}$ long string. The string has two adjacent resonances }

\text{at frequencies of $85.0 \mathrm{~Hz}$ and $102 \mathrm{~Hz}$.}

\text{What is the length of each loop at the $85.0 \mathrm{~Hz}$ resonance?}

\text{Adjacent resonances} \Rightarrow f_{n+1}-f_n=102-85.0=17 \text{ Hz}

\text{So, the fundamental frequency is}: f_1=17 \text{ Hz}

f_n=n f_1\Rightarrow n=\frac{f_n}{f_1}=\frac{85.0}{17}=5

85.0 \text{ Hz}\text{ is the frequency of the $5^{th}$ harmonic}

\text{The $5^\text{th}$ harmonics has 5 loops. The length of one loop is }d=L/5=160/5=32 \text{ cm}