Data Structure
What is
Data Structure?
Data: is simply a value are set of values of different type which is called data types like string, integer, char etc.
Structure: Way of organizing information, so that it is easier to use
– In simple words we can define data structures as Its a way organizing data in such a way so that data can be easier to use
Why needs
Data Structure?
As data structures are used to store data in an organized form, and since data is the most crucial entity in computer science, the true worth of data structures is clear.
Based on different scenarios, data needs to be stored in a specific format. We have a handful of data structures that cover our need to store data in different formats.
1. Each Data Structure allows data to be stored in specific manner.
2. Data Structure allows efficient data search and retrieval.
3. Specific Data structures are decided to work for specific problems.
4. It allows to manage large amount of data such as large databases and indexing services.
5. Data structures can be used to organize the storage and retrieval of information stored in both main memory and secondary memory.
Type of
Data Structure
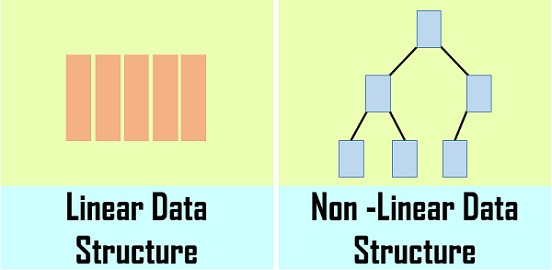
Linear Data Structures: A linear data structure traverses the data elements sequentially, in which only one data element can directly be reached.
Non-Linear Data Structures: Every data item is attached to several other data items in a way that is specific for reflecting relationships. The data items are not arranged in a sequential structure.
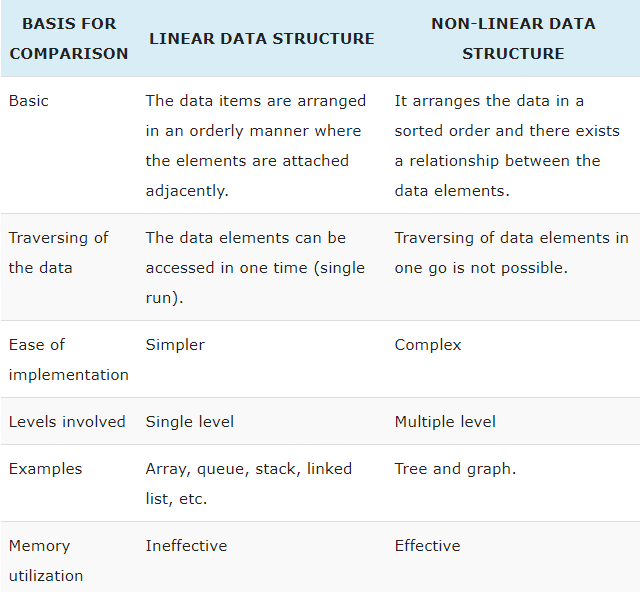
Linear Data Structures
- Array
- Stack
- Queue
- Linked List
Array
Arrays
Array is a container which can hold a fix number of items and these items should be of the same type. Most of the data structures make use of arrays to implement their algorithms.
- The arrangement in an array in a systematic order as a sequential.
- An array stored in a systematic order it given and sequential index.
- Array index start with zero.
- Each array element can be accessed by its index.
-
Element − Each item stored in an array is called an element.
-
Index − Each location of an element in an array has a numerical index, which is used to identify the element.

-
Traverse − Print all the array elements one by one.
-
Insertion − Adds an element at the given index.
-
Deletion − Deletes an element at the given index.
-
Search − Searches an element using the given index or by the value.
-
Update − Updates an element at the given index.
Basic Operations
In computer programming, the most of the cases requires to store the large number of data of similar type. To store such amount of data, it is better to define an array and store all the elements into it.
Application of Array
Stack
- A stack is an Abstract Data Type (ADT), commonly used in most programming languages. It is named stack as it behaves like a real-world stack, for example – a deck of cards or a pile of plates, etc.

- A real-world stack allows operations at one end only. For example, we can place or remove a card or plate from the top of the stack only. Likewise, Stack ADT allows all data operations at one end only. At any given time, we can only access the top element of a stack.
This feature makes it LIFO data structure. LIFO stands for Last-in-first-out.
Operations on Stack
There are various operations which can be performed on stack.
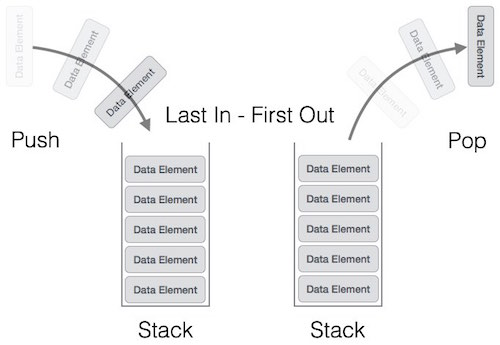
Operations on Stack
Push : Adding an element onto the stack
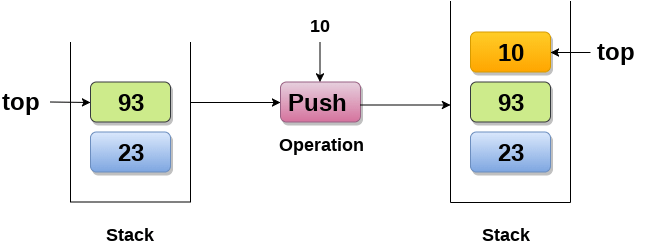
Operations on Stack
Pop : Removing an element from the stack
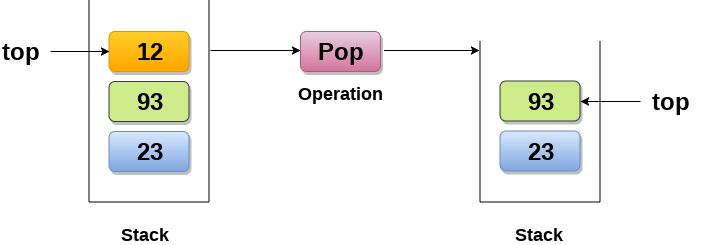
Applications of Stack
- Expression Evaluation
- Expression Conversion
-
Backtracking
- Parenthesis Checking
- String Reversal
- Function Call
Applications of Stack
String Reversal
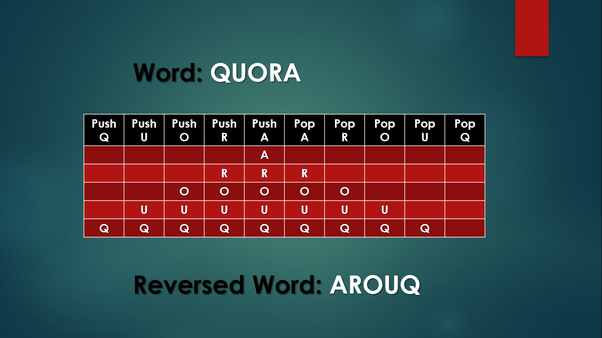
Applications of Stack
Function Call:
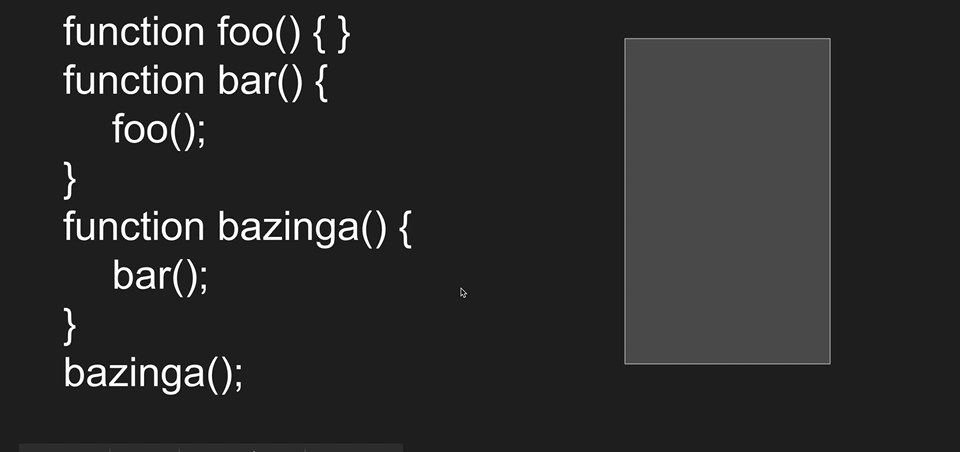
https://cdn-images-1.medium.com/max/1000/1*e3qiT_22FbnEep63BJN2_g.gif
Queue
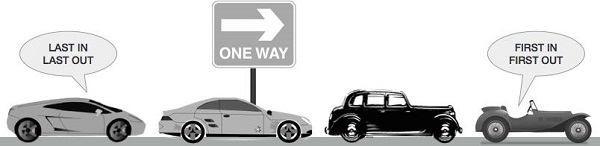
- Queue is an abstract data structure, somewhat similar to Stacks. Unlike stacks, a queue is open at both its ends. One end is always used to insert data (enqueue) and the other is used to remove data (dequeue). Queue follows
- First-In-First-Out methodology, i.e., the data item stored first will be accessed first.

- A real-world example of queue can be a single-lane one-way road, where the vehicle enters first, exits first. More real-world examples can be seen as queues at the ticket windows and bus-stops.
Basic Operations
Enqueue Operation
-
Step 1 − Check if the queue is full.
-
Step 2 − If the queue is full, produce overflow error and exit.
-
Step 3 − If the queue is not full, increment rear pointer to point the next empty space.
-
Step 4 − Add data element to the queue location, where the rear is pointing.
-
Step 5 − return success.
Basic Operations
Enqueue Operation
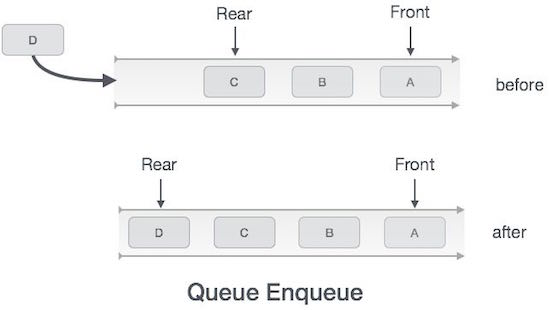
Basic Operations
Dequeue Operation
-
Step 1 − Check if the queue is empty.
-
Step 2 − If the queue is empty, produce underflow error and exit.
-
Step 3 − If the queue is not empty, access the data where front is pointing.
-
Step 4 − Increment front pointer to point to the next available data element.
-
Step 5 − Return success.
Basic Operations
Dequeue Operation
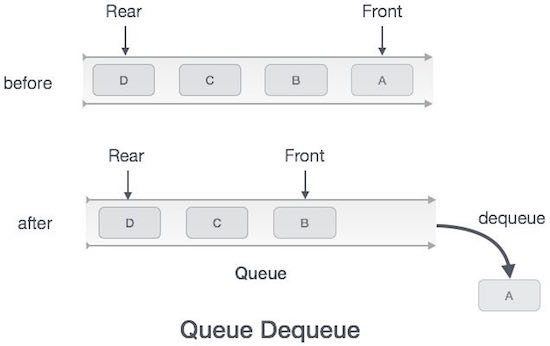
Applications of Queue
- CPU Scheduling and Disk Scheduling.
- Printer Queue: Jobs submitted to the printer are printed in the order of arrival.
- Transferring data asynchronously between two processes (File I/O, Pipes, I/O buffers, etc.)
- Queue at ticket-counters or hospitals.
Linked List
- Linked List can be defined as collection of objects called nodes that are randomly stored in the memory.
- A node contains two fields i.e. data stored at that particular address and the pointer which contains the address of the next node in the memory.
- The last node of the list contains pointer to the null.
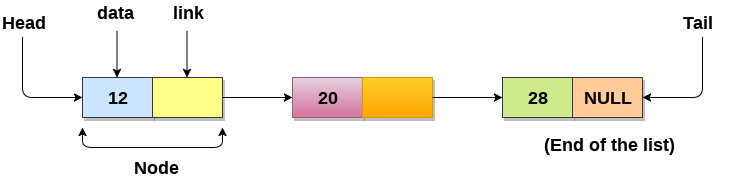
- Linked List contains a link element called first.
- Each link carries a data field(s) and a link field called next.
- Each link is linked with its next link using its next link.
- Last link carries a link as null to mark the end of the list.
Linked List Representation

-
Simple Linked List − Item navigation is forward only.
-
Doubly Linked List − Items can be navigated forward and backward.
Types of Linked List
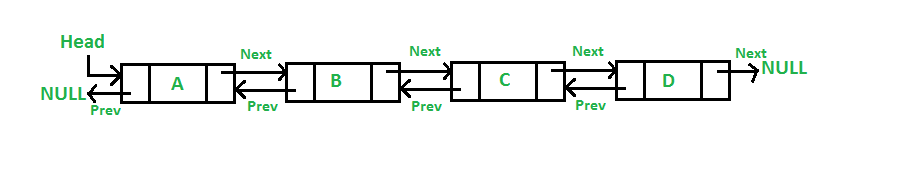
-
Circular Linked List − Last item contains link of the first element as next and the first element has a link to the last element as previous.
Types of Linked List
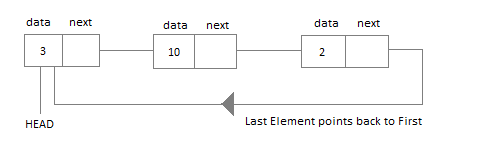
-
Insertion − Adds an element at the beginning of the list.
-
Deletion − Deletes an element at the beginning of the list.
-
Display − Displays the complete list.
-
Search − Searches an element using the given key.
-
Delete − Deletes an element using the given key.
Basic Operations
Applications of Queue
- CPU scheduling: In the preemptive scheduling of processes, based on the priorities in the wait queue the processes are scheduled in the ready queue. Some architectures implement using priority queues and some implement using linked lists.
- In Blockchain and Distributed Ledger Technologies, each block contains the information of the parent block that is hashed. The head of the list can be related to the genesis block. The blockchain correctness can be verified by traversing the blocks.
Non-Linear Data Structures
- Tree
- Graph
Tree
- Tree is a hierarchical data structure which stores the information naturally in the form of hierarchy style.
- Tree is one of the most powerful and advanced data structures.
- It is a non-linear data structure compared to arrays, linked lists, stack and queue.
- It represents the nodes connected by edges.
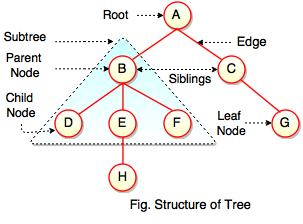
Structure of Tree
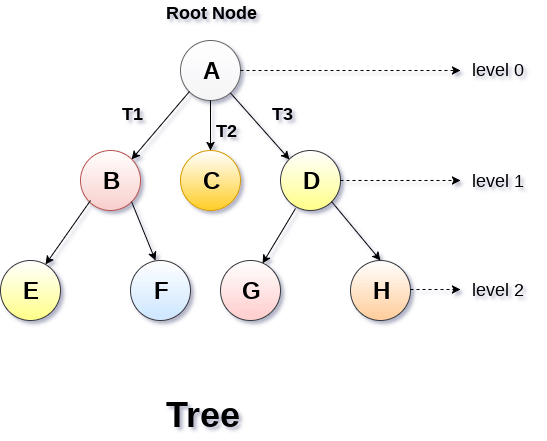
Levels of a node represents the number of connections between the node and the root. It represents generation of a node. If the root node is at level 0, its next node is at level 1, its grand child is at level 2 and so on. Levels of a node can be shown as follows:
- If node has no children, it is called Leaves or External Nodes.
- Nodes which are not leaves, are called Internal Nodes. Internal nodes have at least one child.
- A tree can be empty with no nodes or a tree consists of one node called the Root.
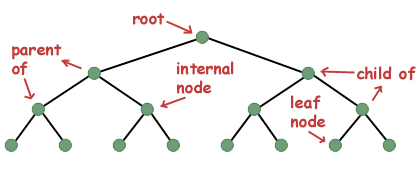

- Tree reflects structural relationships in the data.
- It is used to represent hierarchies.
- It provides an efficient insertion and searching operations.
- Trees are flexible. It allows to move subtrees around with minimum effort.
Advantages of Tree
Type of
Tree
Forest is a collection of disjoint trees. In other words, we can also say that forest is a collection of an acyclic graph which is not connected.
1. Forest
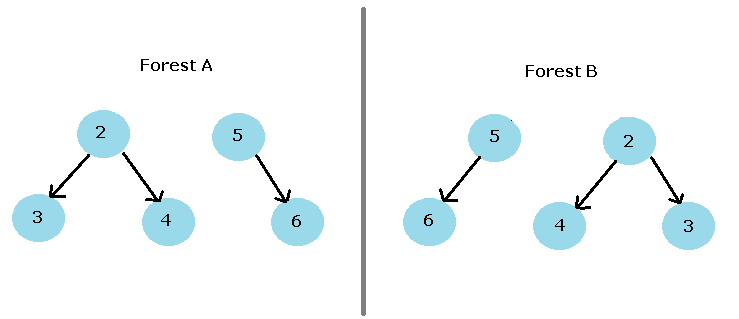
Big Data and Web Scrapers
Uses of Forest Data Structure
Websites are organized in the form of a tree data structure where the main page forms the root node and the subsequent hyperlinks from that page represents the rest of the tree. When Web scrapers scrap multiple such websites, they represent it in the form of a forest of several trees.
A binary tree is a tree in which no node has more than two children, and every child is either a left child or a right child even if it is the only child its parent has.
2. Binary tree
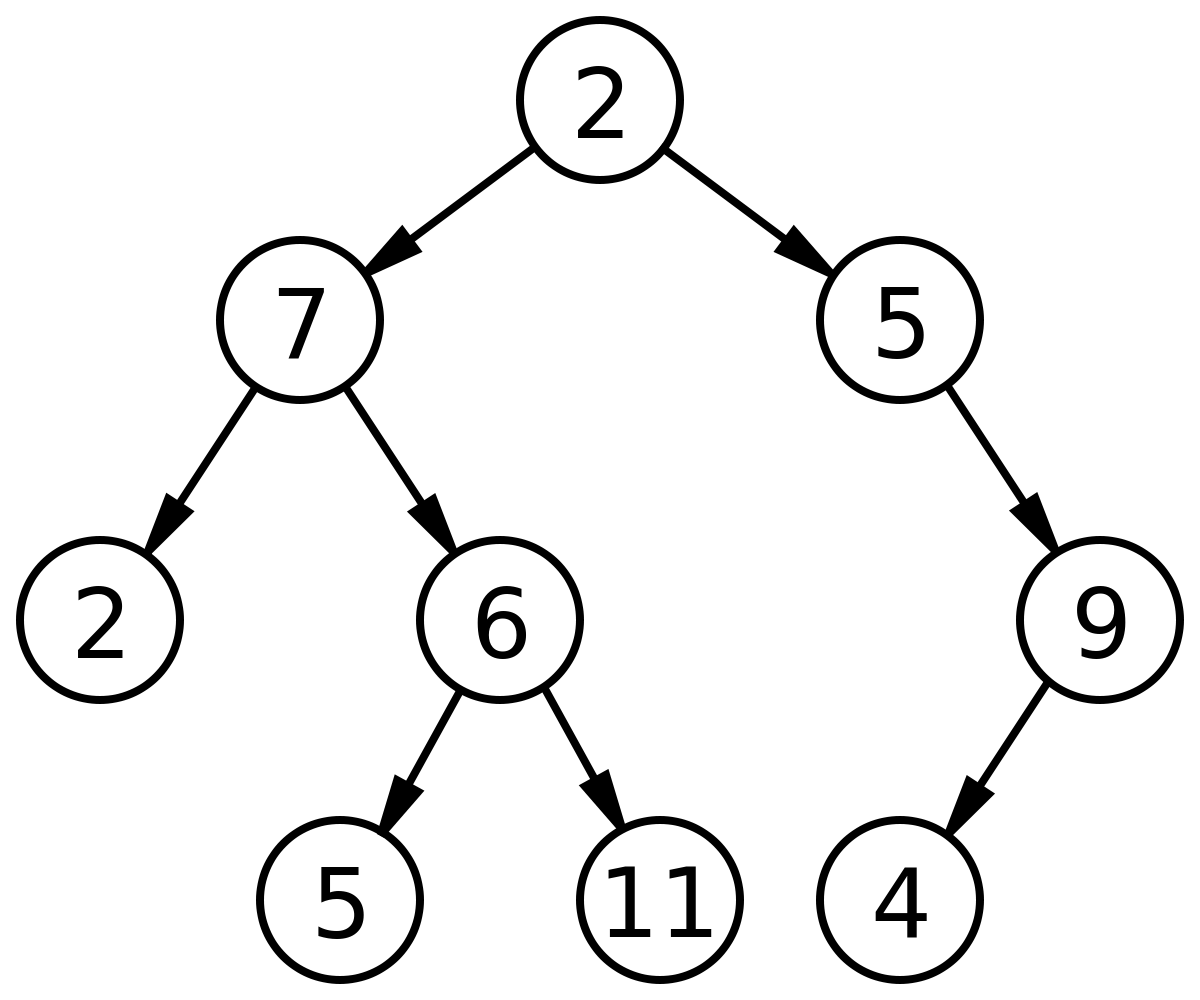
A decision tree is a tree in which each internal node contains a question or an option that has a finite number of responses. When there are two possible responses, the tree is a binary decision tree. Nodes that are conclusions are leaf nodes.
Binary tree as Decision Tree
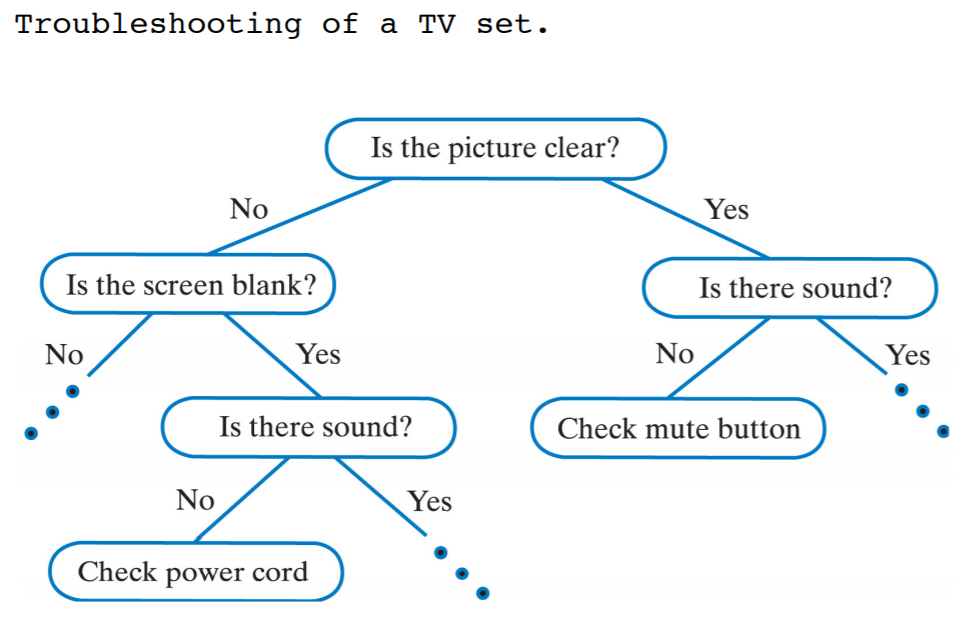
The data of all the nodes in the left sub-tree of the root node should be ≤ the data of the root. The data of all the nodes in the right subtree of the root node should be > the data of the root.
3. Binary search tree
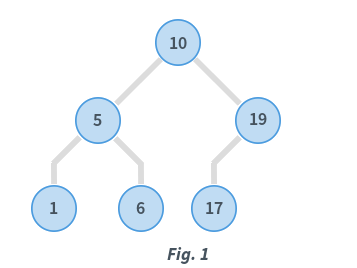
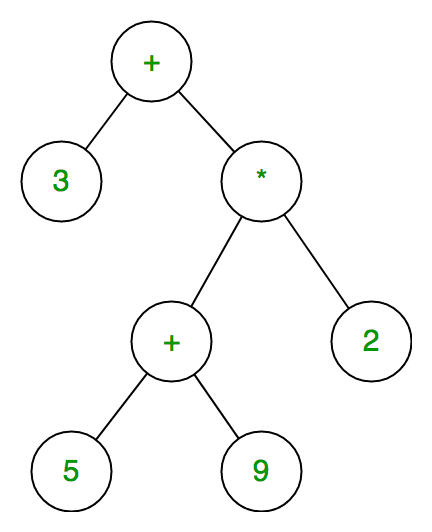
In Fig. 1, consider the root node with data = 10.
- Data in the left subtree is: [5,1,6]
- All data elements are < 10
- Data in the right subtree is: [19,17]
- All data elements are > 10
Expression tree is a binary tree in which each internal node corresponds to operator and each leaf node corresponds to operand so for example expression tree for 3 + ((5+9)*2) would be:
4. Expression Tree
Graph
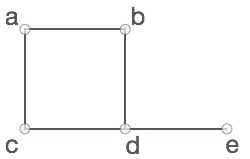
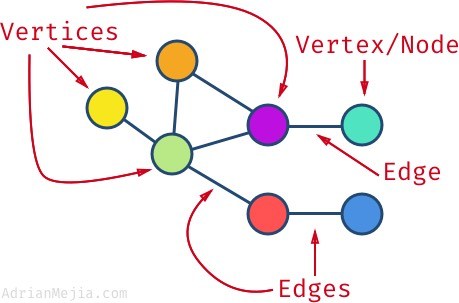
A graph is a pictorial representation of a set of objects where some pairs of objects are connected by links. The interconnected objects are represented by points termed as vertices, and the links that connect the vertices are called edges.
Graph Data Structure
-
Vertex − Each node of the graph is represented as a vertex.
-
Edge − Edge represents a path between two vertices or a line between two vertices.
-
Adjacency − Two node or vertices are adjacent if they are connected to each other through an edge. In the following example, B is adjacent to A, C is adjacent to B, and so on.
-
Path − Path represents a sequence of edges between the two vertices. In the following example, ABCD represents a path from A to D.
Graph Data Structure
Basic Operations
Following are basic primary operations of a Graph −
-
Add Vertex − Adds a vertex to the graph.
-
Add Edge − Adds an edge between the two vertices of the graph.
-
Display Vertex − Displays a vertex of the graph.
Type of Graph
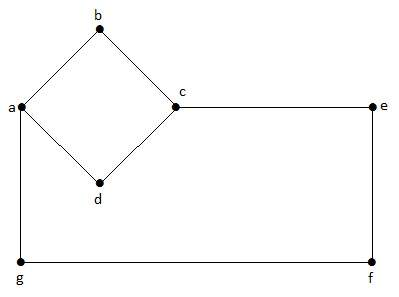
Finite Graphs: A graph is said to be finite if it has finite number of vertices and finite number of edges.
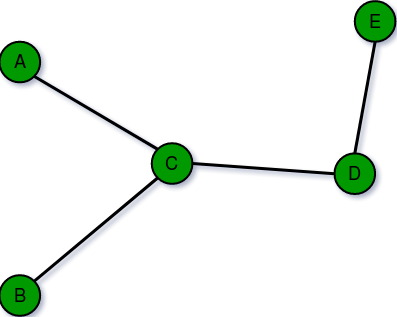
Type of Graph
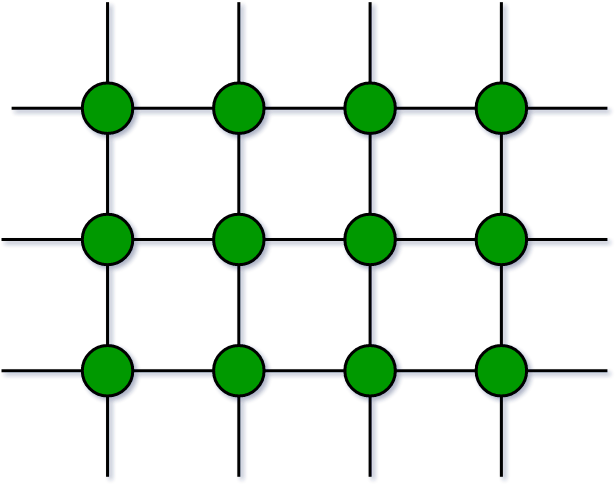
Infinite Graph: A graph is said to be infinite if it has infinite number of vertices as well as infinite number of edges.
Type of Graph
Simple graph: it is a graph which does not contains more than one edge between the pair of vertices. A simple railway tracks connecting different cities is an example of simple graph.
Type of Graph
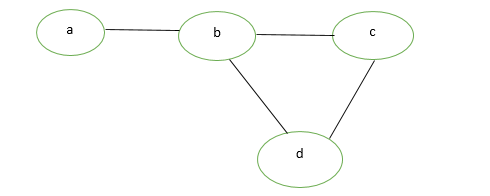
Non-Directed Graph: A non-directed graph contains edges but the edges are not directed ones.
Type of Graph
Directed Graph: A directed graph contains edges where each edge is associated with an ordered pair of vertices.

Type of Graph
Weighted Graph: A directed graph contains edges where each edge also has an associated real number with it, known as the edge weight.

Data Structures to Store Graphs
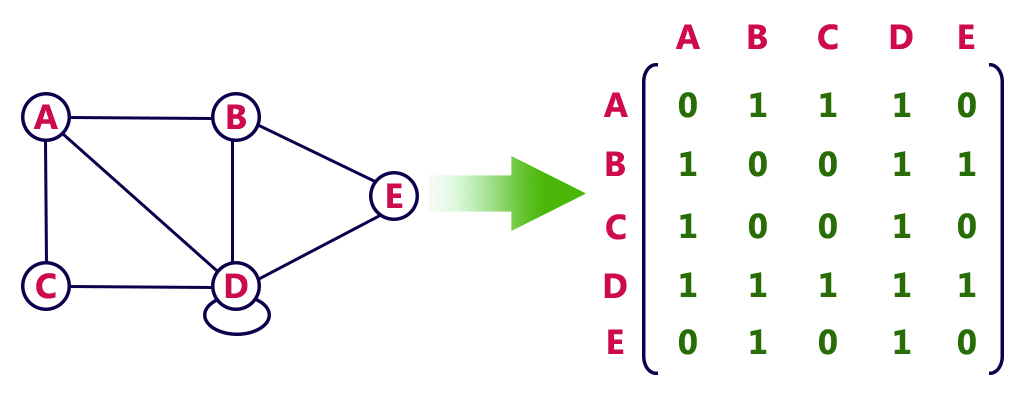
Adjacency Matrix: The standard adjacency matrix stores a matrix as a 2-D array with each slot in A[i][j] being a 1 if there is an edge from vertex i to vertex j, or storing a 0 otherwise.
Applications of Graph
- Facebook: Each user is represented as a vertex and two people are friends when there is an edge between two vertices. Similarly friend suggestion also uses graph theory concept.
- Google Maps: Various locations are represented as vertices and the roads are represented as edges and graph theory is used to find shortest path between two nodes.
- Recommendations on e-commerce websites: The “Recommendations for you” section on various e-commerce websites uses graph theory to recommend items of similar type to user’s choice.
- Graph theory is also used to study molecules in chemistry and physics.
Thank you
Data Structure
By Sofwan Abdulwahab
Data Structure
- 575



