Data Structure
Deep Dive Part 2
Recap
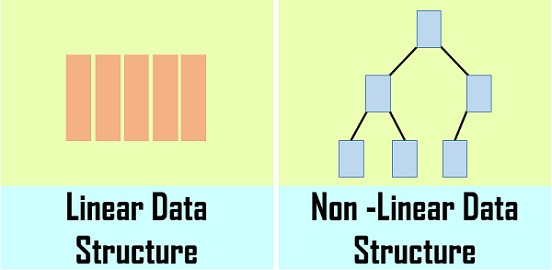
Linear Data Structures: A linear data structure traverses the data elements sequentially, in which only one data element can directly be reached.
Non-Linear Data Structures:
Every data item is attached to several other data items in a way that is specific for reflecting relationships. The data items are not arranged in a sequential structure.
Big-O Notation
- Big O notation is used in Computer Science to describe the performance or complexity of an algorithm.
- Big O specifically describes the worst-case scenario and the execution time required or the space used by an algorithm.
Big-O Notation
- Big O notation is used in Computer Science to describe the performance or complexity of an algorithm.
- Big O specifically describes the worst-case scenario and the execution time required or the space used by an algorithm.
- It can measure how the performance of an algorithm changes, based on the size of the input set of data.
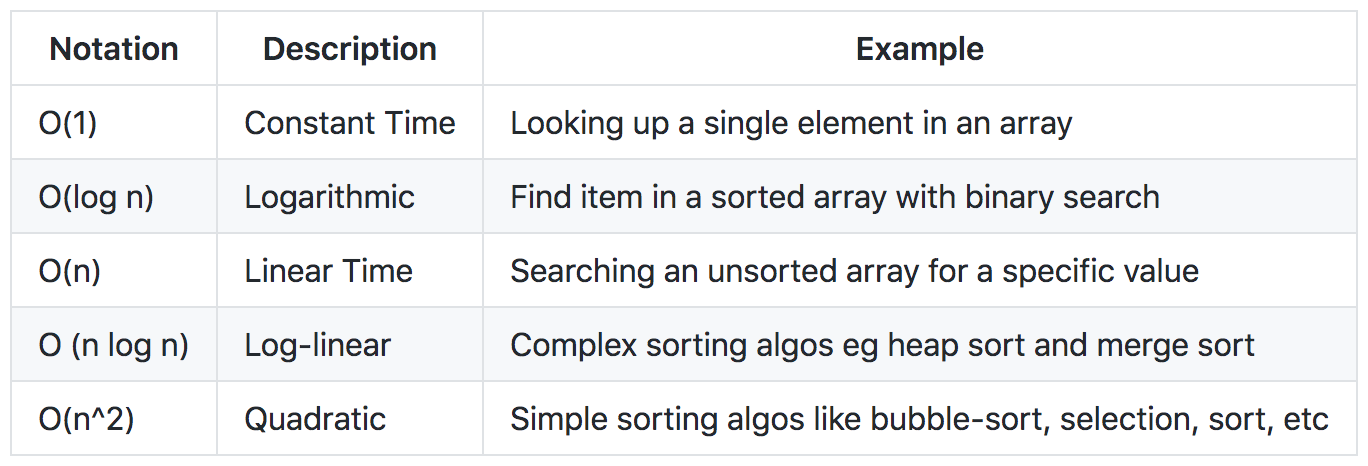
Examples of Big O notations
Objectives
Tree
- Definition of tree data structure
- Tree traversal
- Type of tree
- Operations of each type of tree
- Use case of each type of tree
- Time complexity of each type of tree
Tree
A tree is a non-linear data structure where a node can have zero or more children. Each node contains a value. Like graphs, the connection between nodes is called edges. A tree is a type of graph, but not all of them are trees
Data structure resembles a tree. It starts with a root node and branch off with its descendants, and finally, there are leaves.
What is Tree Data Structure?
Why, Tree Data Structure?
- Representing hierarchical data
- Storing data in a way that makes it easily searchable
- Representing sorted lists of data
- As a workflow for compositing digital images for visual effects
- Routing algorithms
Tree Data Structure
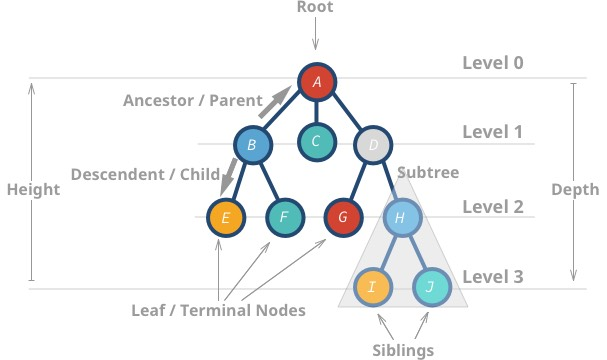
- The top-most node is called root.
- A node without children is called leaf node or terminal node.
-
Height (h) of the tree is the distance (edge count) between the farthest leaf to the root.
- A has a height of 3
- I has a height of 0
-
Depth or level of a node is the distance between the root and the node in question.
- H has a depth of 2
- B has a depth of 1
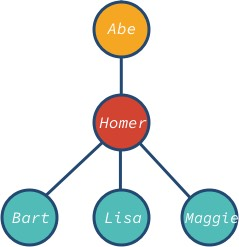
Simple Tree
The node abe is the root and bart, lisa and maggie are the leaf nodes of the tree. Notice that the tree’s node can have a different number of descendants: 0, 1, 3, or any other value.
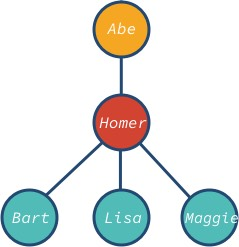
Simple Tree
Tree data structures have many applications such as:
-
Databases
-
Priority Queues
-
Querying an LDAP (Lightweight Directory Access Protocol)
-
Representing the Document Object Model (DOM) for HTML on Websites.
Tree Traversal
Tree Traversal
Traversal is a process to visit all the nodes of a tree and may print their values too. Because, all nodes are connected via edges (links) we always start from the root (head) node. That is, we cannot randomly access a node in a tree.
Generally, we traverse a tree to search or locate a given item or key in the tree or to print all the values it contains.
1. Pre-order Traversal (Root, Left, Right)
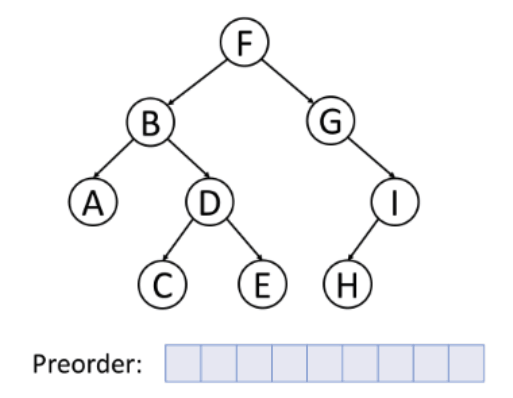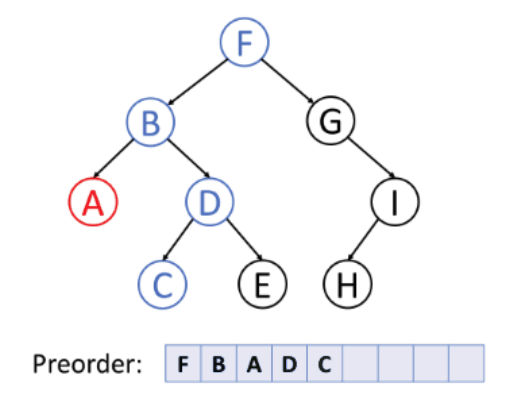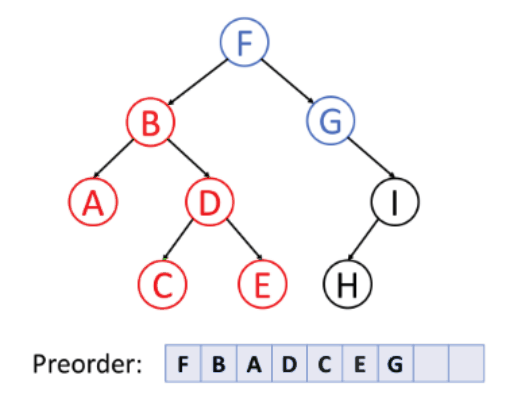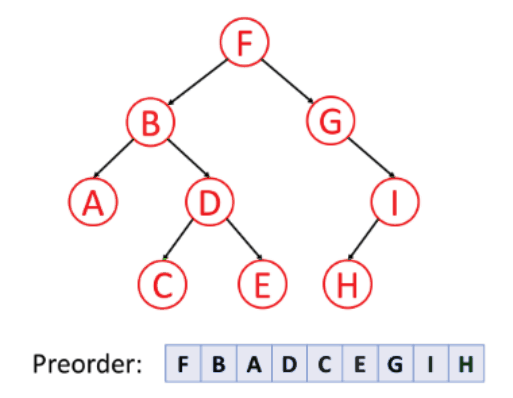
In this traversal method, the root node is visited first, then the left subtree and finally the right subtree. Preorder traversal is used to create a copy of the tree.
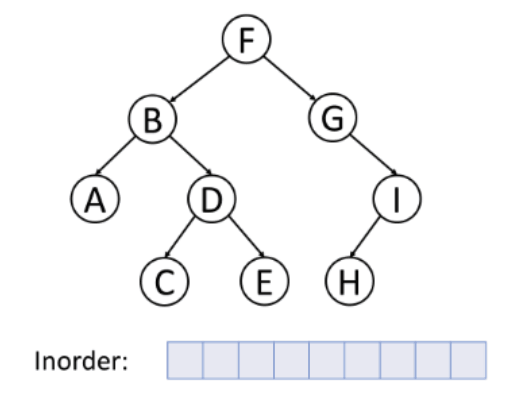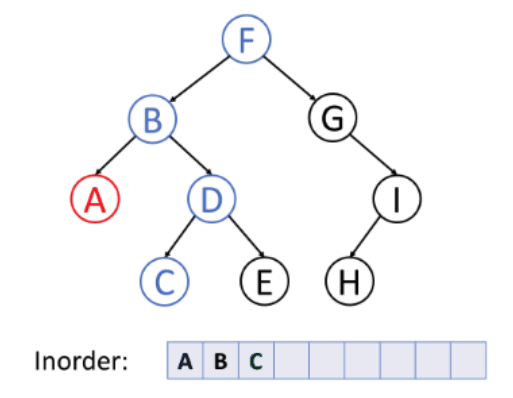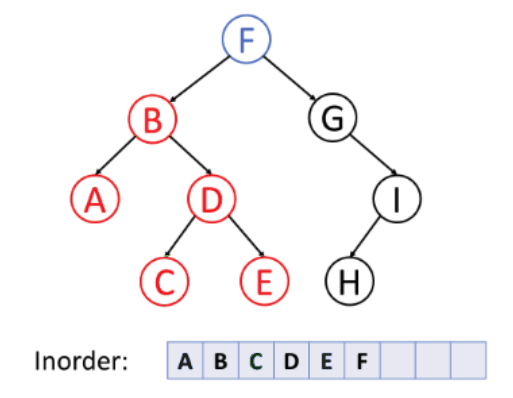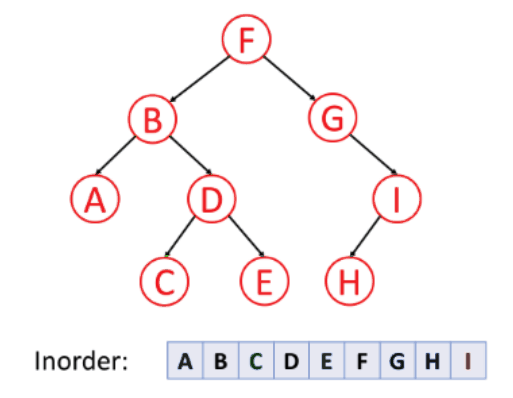
2. In-order Traversal (Left, Root, Right)
In this traversal method, the left subtree is visited first, then the root and later the right sub-tree. We should always remember that every node may represent a subtree itself.
If a binary tree is traversed in-order, the output will produce sorted key values in an ascending order.
3. Post-order Traversal (Left, Right, Root)
In this traversal method, the root node is visited last, hence the name. First we traverse the left subtree, then the right subtree and finally the root node. Postorder traversal is used to delete the tree.
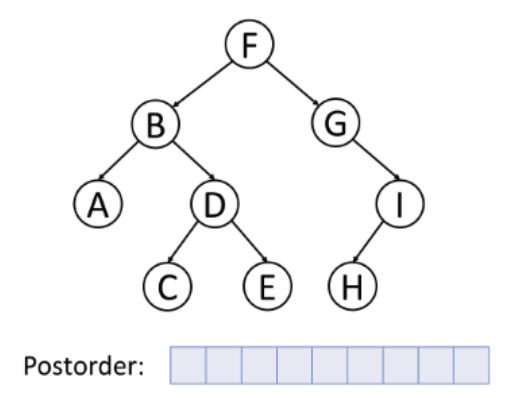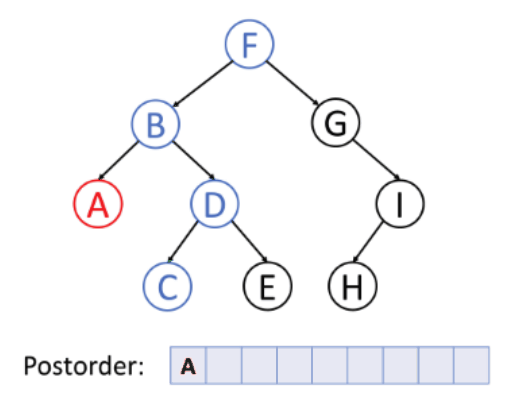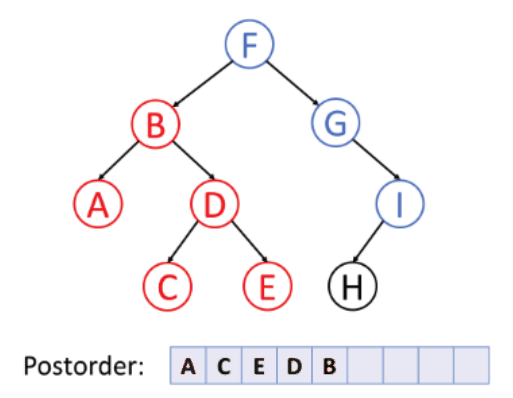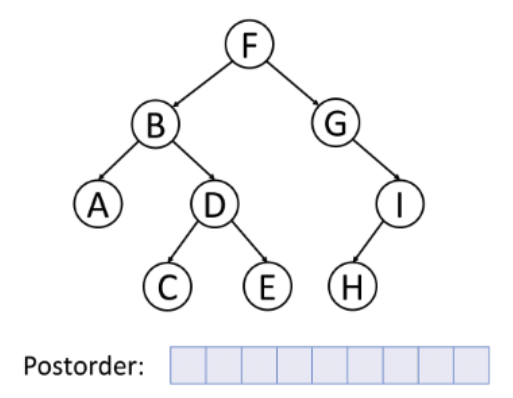
Type of Tree
1. Binary Trees
Trees nodes can have zero or more children. However, when a tree has at the most two children, then it’s called binary tree.
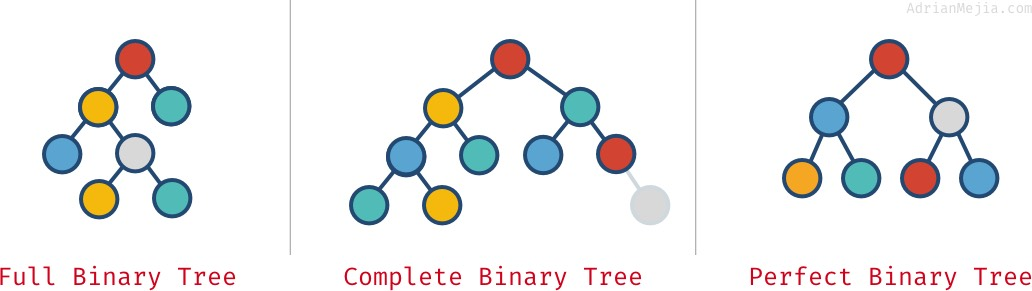
Depending on how nodes are arranged in a binary tree, it can be full, complete and perfect:
- Full binary tree: each node has exactly 0 or 2 children (but never 1).
- Complete binary tree: when all levels except the last one are full with nodes.
- Perfect binary tree: when all the levels (including the last one) are full of nodes.
-
A perfect tree is always complete and full.
- Perfect binary trees have precisely 2^k−1 nodes, where k is the last level of the tree (starting with 1).
-
A complete tree is not always full.
- Like in our “complete” example, since it has a parent with only one child. If we remove the rightmost gray node, then we would have a complete and full tree but not perfect.
- A full tree is not always complete and perfect.
The data of all the nodes in the left sub-tree of the root node should be ≤ the data of the root. The data of all the nodes in the right subtree of the root node should be > the data of the root.
2. Binary search tree
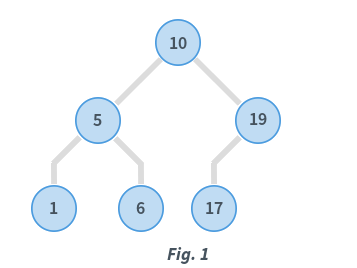
In Fig. 1, consider the root node with data = 10.
- Data in the left subtree is: [5,1,6]
- All data elements are < 10
- Data in the right subtree is: [19,17]
- All data elements are > 10
Whenever an element is to be searched, start searching from the root node. Then if the data is less than the key value, search for the element in the left subtree. Otherwise, search for the element in the right subtree. Follow the same algorithm for each node.
Search Operation
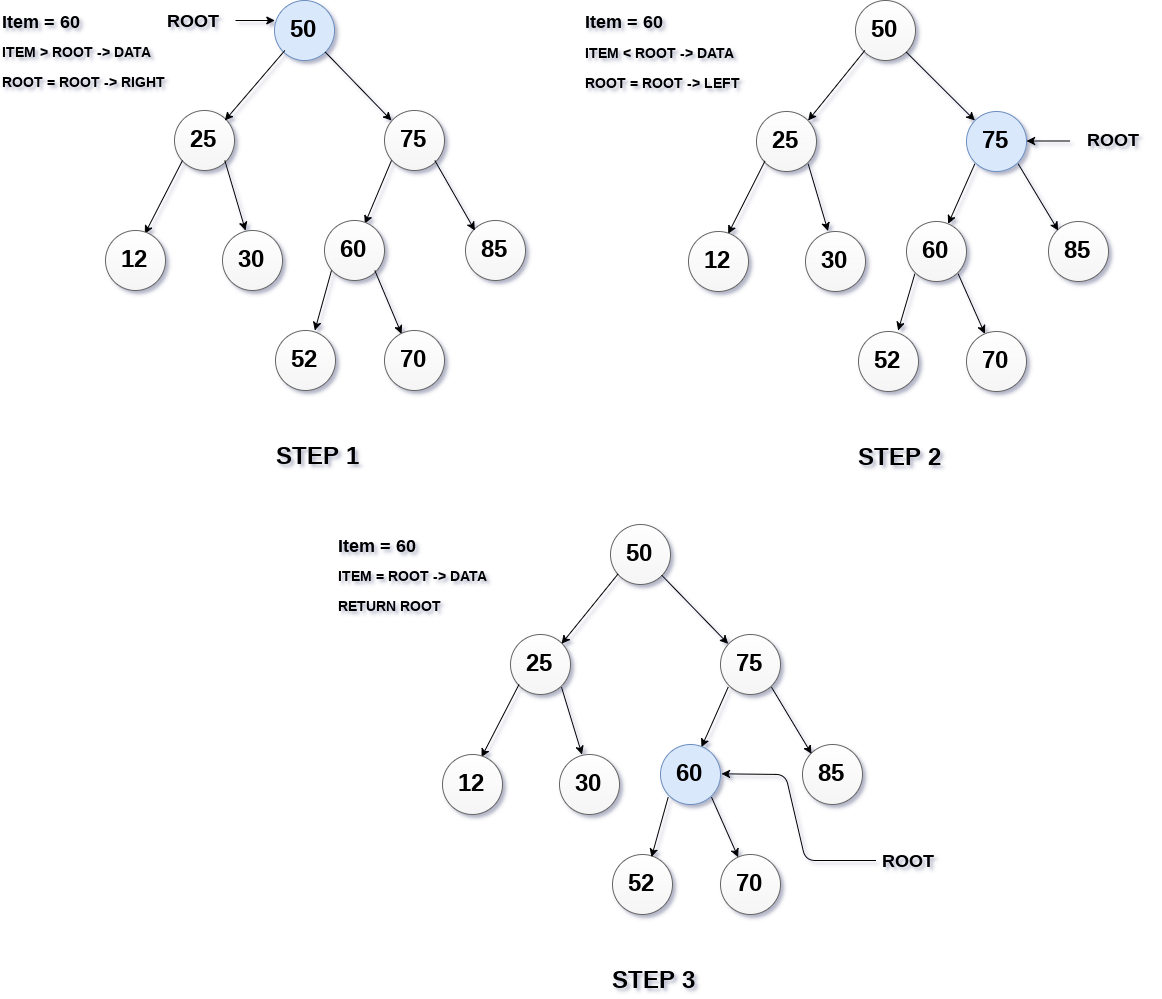
Whenever an element is to be searched, start searching from the root node. Then if the data is less than the key value, search for the element in the left subtree. Otherwise, search for the element in the right subtree. Follow the same algorithm for each node.
Search Operation

Search Operation

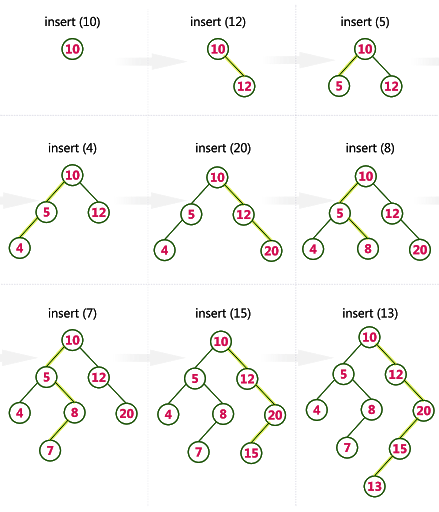
To insert a node in a binary tree, we do the following:
- If a tree is empty, the first node becomes the root.
- Compare root/parent’s value if it’s higher go right, if it’s lower go left. If it’s the same, then the value already exists so you can increase the duplicate count (multiplicity).
- Repeat #2 until we found an empty slot to insert the new node.
Node Insertion
Node Insertion
Node Deletion
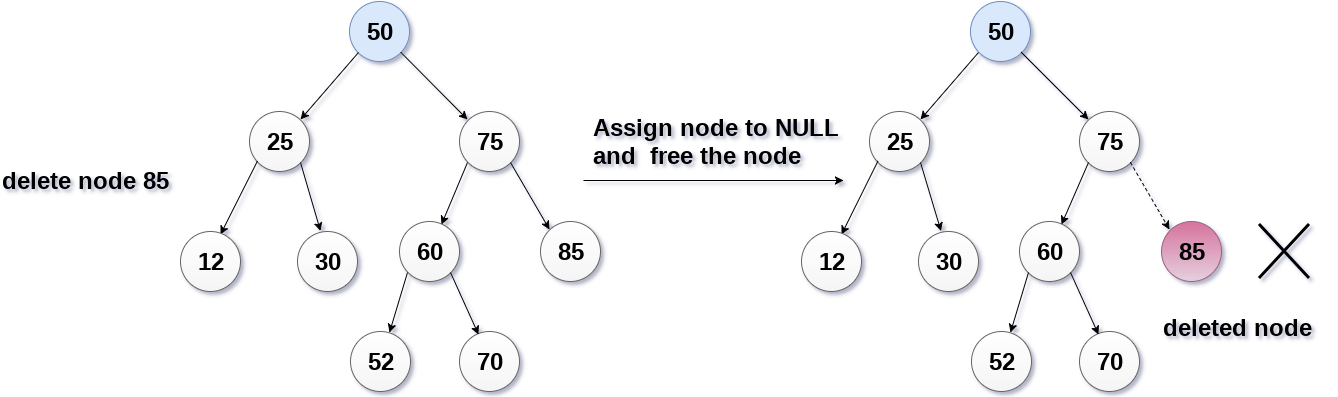
Case 1: The node to be deleted is a leaf node
Case 2: The node to be deleted has only one child.
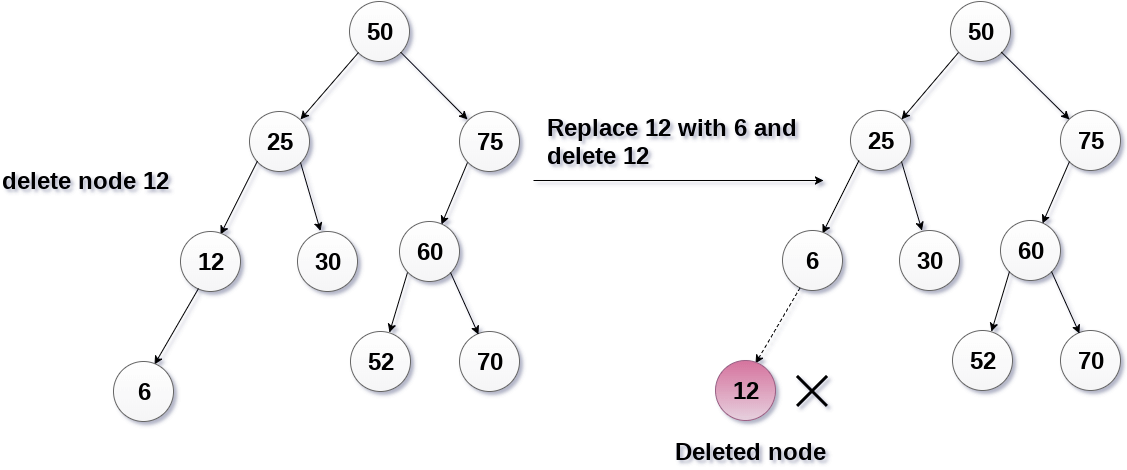
Case 3: The node to be deleted has two children.
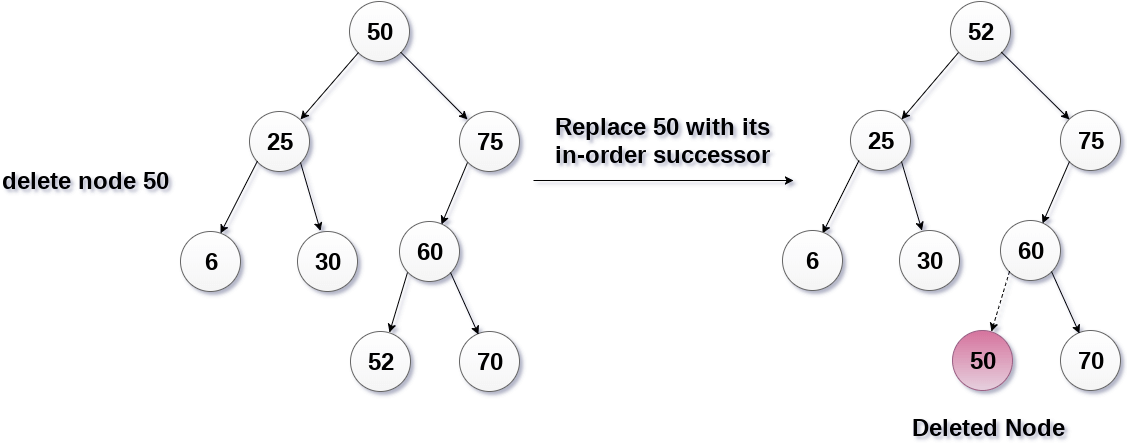
The node 50 is to be deleted which is the root node of the tree.
The in-order traversal of the tree given below.
6, 25, 30, 50, 52, 60, 70, 75.
replace 50 with its in-order successor 52. Now, 50 will be moved to the leaf of the tree, which will simply be deleted.
Advantages of using binary search tree
- Searching become very efficient in a binary search tree since, we get a hint at each step, about which sub-tree contains the desired element.
- The binary search tree is considered as efficient data structure in compared to arrays and linked lists. In searching process, it removes half sub-tree at every step.
- It also speed up the insertion and deletion operations as compare to that in array and linked list.
Use case
Time Analysis
It is used to find a specific value in a sorted collection of items by reducing the search scope by half until an item is found or not found. It is used with a sorted collection of items.
Searching for an element in a binary search tree takes O(log2n) time. In worst case, the time it takes to search an element is O(n).
3. AVL tree
An AVL tree is a subtype of binary search tree. Named after it's inventors Adelson, Velskii and Landis, AVL trees have the property of dynamic self-balancing in addition to all the properties exhibited by binary search trees.
Tree is said to be balanced if balance factor of each node is in between -1 to 1, otherwise, the tree will be unbalanced and need to be balanced.
Balance Factor (k) = height (left(k)) - height (right(k))
- If balance factor of any node is 1, it means that the left sub-tree is one level higher than the right sub-tree.
- If balance factor of any node is 0, it means that the left sub-tree and right sub-tree contain equal height.
- If balance factor of any node is -1, it means that the left sub-tree is one level lower than the right sub-tree.
Balance Factor
Balance Factor
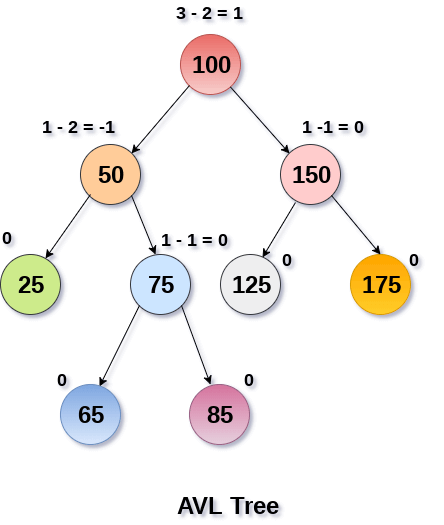
If balance factor is not between -1, 0, 1, how to balance the tree?
AVL Tree Rotations
Rotation is the process of moving nodes either to left or to right to make the tree balanced. There are four rotations and they are classified into two types.
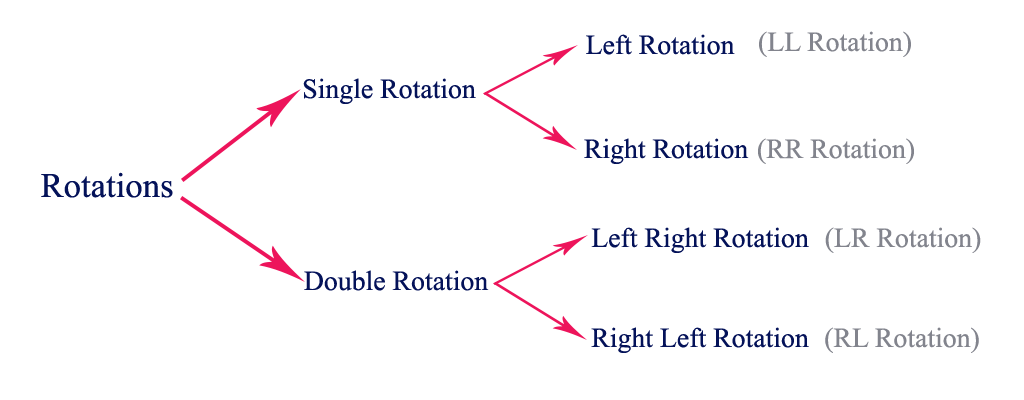
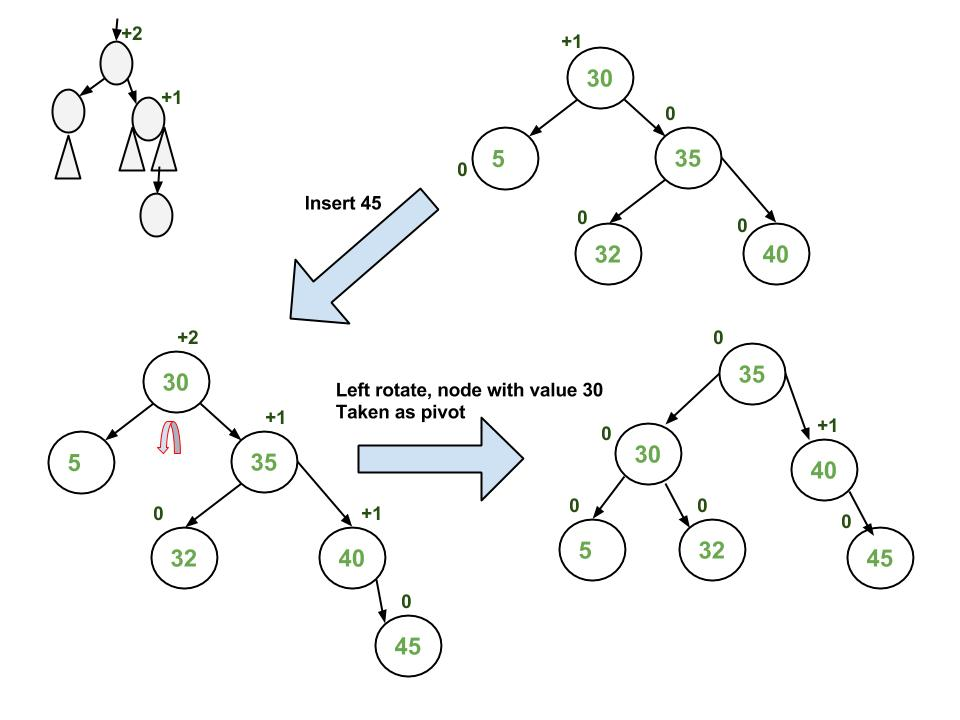
Single Left Rotation (LL Rotation)
In LL Rotation, every node moves one position to left from the current position. To understand LL Rotation, let us consider the following insertion operation in AVL Tree
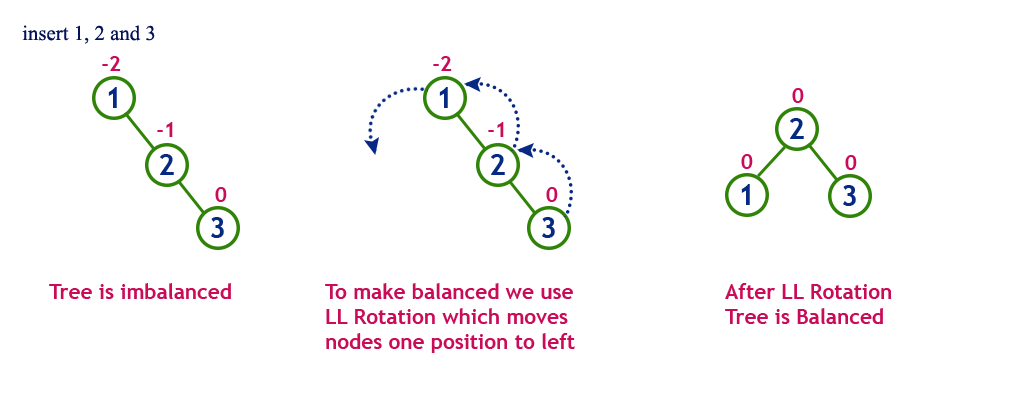
Single Right Rotation (RR Rotation)
In RR Rotation, every node moves one position to right from the current position. To understand RR Rotation, let us consider the following insertion operation in AVL Tree.
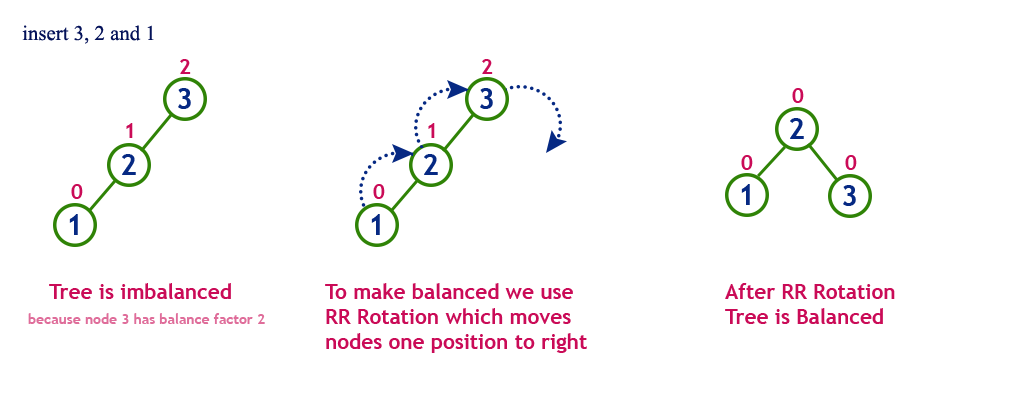
Left Right Rotation (LR Rotation)
The LR Rotation is a sequence of single left rotation followed by a single right rotation. In LR Rotation, at first, every node moves one position to the left and one position to right from the current position. To understand LR Rotation, let us consider the following insertion operation in AVL Tree.
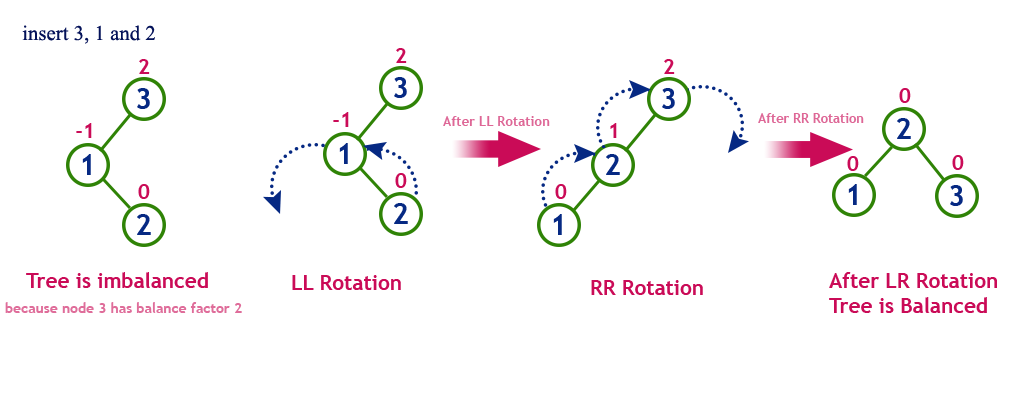
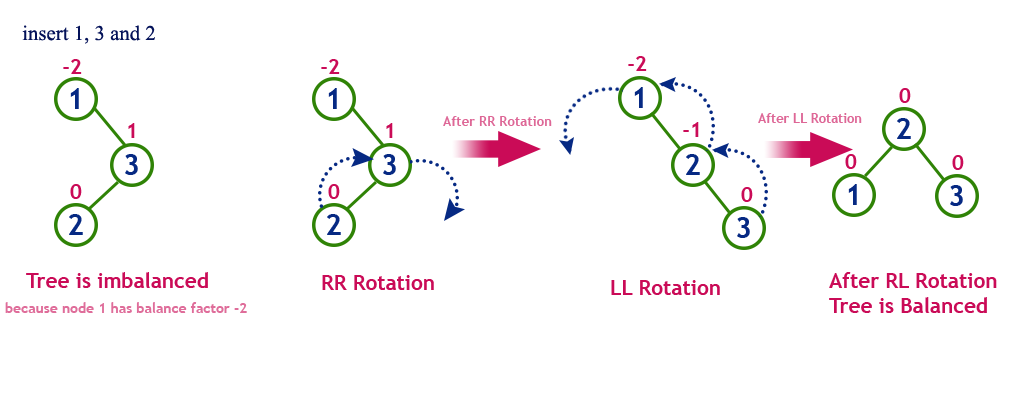
Right Left Rotation (RL Rotation)
The RL Rotation is sequence of single right rotation followed by single left rotation. In RL Rotation, at first every node moves one position to right and one position to left from the current position. To understand RL Rotation, let us consider the following insertion operation in AVL Tree.
AVL Insertion & Deletion
You will do an insertion or deletion similar to a normal Binary Search Tree insertion. After inserting, you fix the AVL property using left or right rotations.
Time Analysis of AVL Trees
AVL tree controls the height of the binary search tree by not letting it to be skewed. The time taken for all operations in a binary search tree of height h is O(h). However, it can be extended to O(n) if the BST becomes worst case. By limiting this height to log n, AVL tree imposes an upper bound on each operation to be O(log n) where n is the number of nodes.
Application of AVL Trees
AVL trees are beneficial in the cases where you are designing some database where insertions and deletions are not that frequent but you have to frequently look-up for the items present in there.
Implement Tree in JavaScript

Implement TreeNode Class

Create TreeNode Classes
More...
Conclusion
-
The tree is a data structure where a node has 0 or more descendants/children.
-
Tree nodes don’t have cycles (acyclic). If it has cycles, it is a Graph data structure instead.
-
Trees with two children or less are called: Binary Tree
-
When a Binary Tree is sorted in a way that the left value is less than the parent and the right children is higher, then and only then we have a Binary Search Tree.
-
You can visit a tree in a pre/post/in-order fashion.
Thank you
Data Structure Deep Dive Part 2
By Sofwan Abdulwahab
Data Structure Deep Dive Part 2
- 491



