Computational Protein Design

Proteins

Proteins are sequences of amino acids that are essential to many bodily functions.

Protein structure is closely related to protein function.

Individual amino acids attract/repel one another.

The protein tends to fold into conformations that minimize its free energy.

What is Computational Protein Design?

Computational Protein Design (CPD) tries to, given a protein structure, find an amino acid sequence that will likely fold into that structure. It is the inverse of the problem of protein folding.

After we know a sequence, we can make that protein in the lab.

CPD has already been used to design proteins for important medical applications (like detecting HIV) and holds promise to treat diseases that involve complex protein-protein interactions (Alzheimer's, cancer, etc.).

Solving a CPD Problem

Challenges

This is an NP-hard combinatorial optimization problem, and the sequence space grows incredibly quickly.

Exact approaches struggle to find solutions for proteins >30 residues long.

The dominant approach (used by Rosetta) is simulated annealing, but this still struggles with >200 residues.

Despite these limitations, computational protein design has already proved to be indispensible.

As a Discrete Optimization Problem

There are 20 naturally occurring amino acids to choose from at each position in the sequence.

Each amino acid residue has a flexible side chain, but we can discretize its bond angles into the most common conformations.

For a given shape, we try to find an amino acid - side chain sequence that minimizes the free energy.

The Energy Matrix

We want to minimize free energy:

$$\text{min} E =  \sum_i E_i(r_i) + \sum_{i \neq j} E_{i j}(r_i, r_j)$$

So we use a CPD program (Rosetta, OSPREY) to calculate an energy matrix for different amino acid-side chain values.

In this energy matrix, self-energies are on the diagonal, and combinations that would double assign/cause sterical clashes (two amino acids in the same place) are given a huge penalty value (say \(2k\)).

Formulation

We also want to ensure that every position does get one assignment. Combining this with the energy matrix, we get the QUBO:

$$\min \left[ \sum_i (e_{i,i} - k)x_i + \sum_{i<j} e_{i,j}x_ix_j \right]$$

where \(k\) is a large penalty term, and \(e_{i,j}\) is the \(i,j\)-th term in the energy matrix (remember \(e_{i,j} = 2k\) when \(x_i, x_j\) not compatible).

The minimum corresponds to the lowest energy sequence for that conformation.

Making it Useful

What do Researchers Need?

Turns out that finding a global optimum is useful, but it alone usually isn't enough to design a protein with a desired function.

The energy function is an approximation, so an ensemble of low energy states is more likely to contain the true physical answer.

We want to characterize the energy landscape, finding a sampling distribution over low energy solutions and intermediary states.

Why QA (Could) Be a Good Fit

To gather this sampling distribution, people typically run a simulated annealing algorithm hundreds of thousands of times.

But researchers have found that SA often gets stuck pretty far away from the best sequences, so many of these runs may be returning solutions that don't matter.

Quantum Annealing is a good method to find a global optimum and sample low energy solutions. In addition, we can stop the process early or adjust the Hamiltonian to observe intermediary states.

Also, the energy matrices tend to be sparse :)

What We Did

Collaborators' Work

We collaborated with two scientists who have been working on the problem for about a year already.

In that time, they developed and implemented the mapping from CPD problem to QUBO matrix, and generated ~6,000 CPD problems of various sizes to test on the D-Wave.

They took one of these design problems, solved it on the D-Wave, and are currently expressing it in a wet lab to experimentally verify if the quantum annealing approach worked.

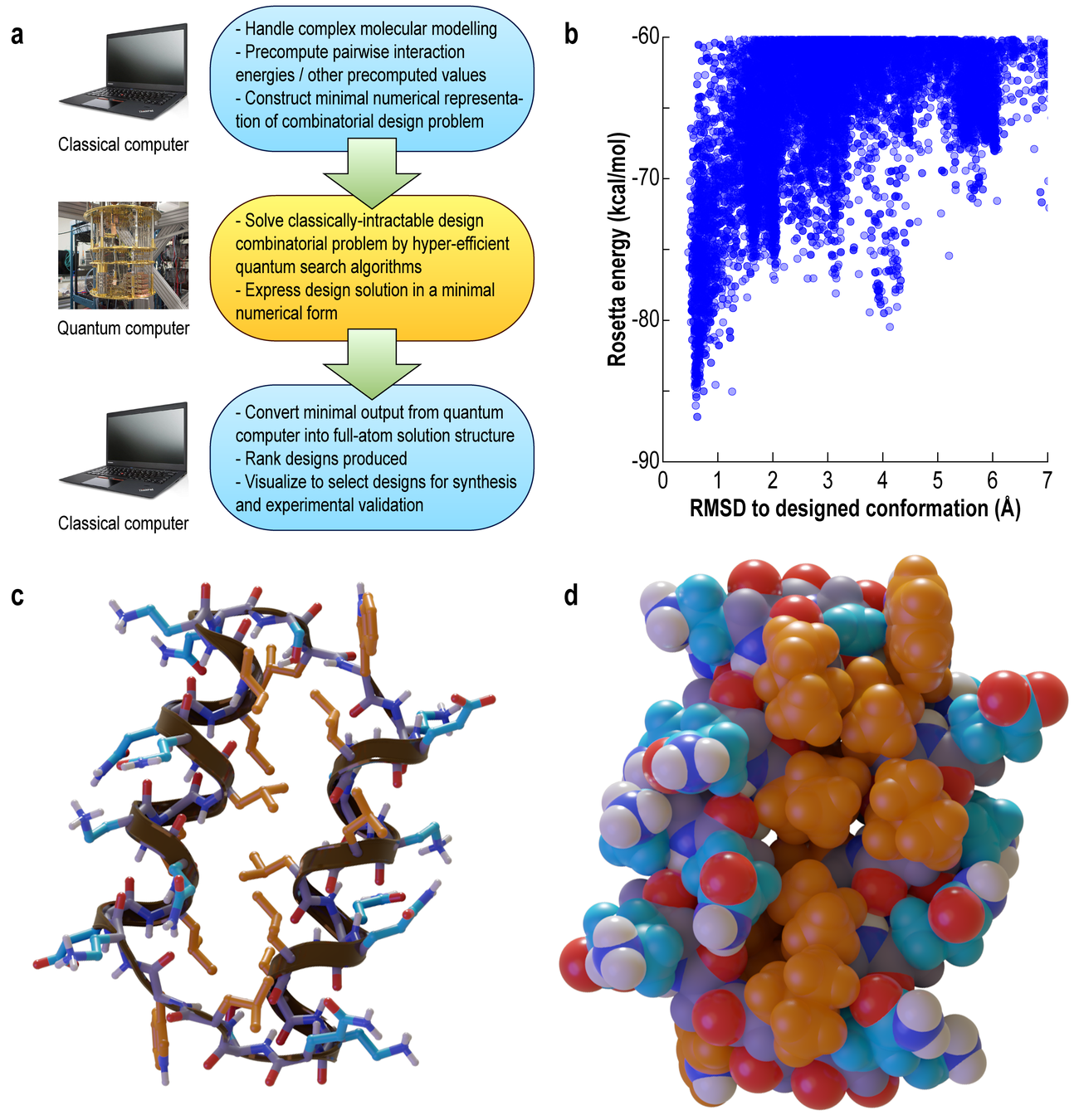
33 residue

quantum-designed protein

Our Work (Ongoing)

Characterizing scaling

Quantum annealing is not yet competitive with classical state-of-the-art solvers. But QA hardware continues improve rapidly.

To make the argument that QA will be a better method once hardware improves, we need to show that our approach scales well as a function of problem size.

We will evaluate scaling on several metrics (energy difference from optimal solution, total annealing time, total iterations).

Our Work (Ongoing)

Improving algorithm for large problems

The D-Wave 2000 series have 2000 very sparsely connected qubits, allowing us to solve CPD problems of up to ~100 variables.