Lecture 8:

Continuous Control

Artyom Sorokin | 13 Apr

Continuous Action Spaces

Deep RL Family Tree:

DQN

Many DQN variants

Policy Gradient

A2C/A3C

REINFORCE/PG+

TRPO

PPO

Value-Based

Policy-Based

Deep RL Family Tree:

Off-Policy

DQN

Many DQN variants

Policy Gradient

A2C/A3C

REINFORCE/PG+

TRPO

PPO

Close to On-Policy

On-Policy

Value-Based

Policy-Based

Deep RL Family Tree:

  • Off-Policy

DQN

Many DQN variants

Policy Gradient

A2C/A3C

REINFORCE/PG+

TRPO

PPO

  • Close to On-Policy
  • On-Policy

Value-Based

Policy-Based

      Discrete Actions:

      Continuous Actions

Where are my off-policy methods for continuous actions?

Problem with Value-Based Methods

Value-Based methods learn to estimate \(Q(s,a)\)

How to get best action action from \(Q\)-values?

a_{best} = argmax_{a'} Q(s,a')

huge number of actions \(\rightarrow\) expensive

continuous action space \(\rightarrow\) solve optimization problem at each \(t\)

Why PG-based methods work:

Recall Policy Gradients (A2C version): 

No need to estimate for (s, a) pairs

Simplest advantage function estimate:

\nabla_{\theta} J(\theta) \approx \textcolor{black}{\frac{1}{N} \sum\limits_{i=1}^{N}} \biggl[ \sum\limits_{t=0}^T \nabla_{\theta}\,log\, \pi_{\theta}(a_{\textcolor{black}{i},t}|s_{\textcolor{black}{i},t}) \textcolor{black}{A_{\pi_{\theta}}(s_{i,t}, a_{i,t})} \biggr]
A_{\pi_{\theta}}(a_t,s_t) \approx r_t + V_{\pi_{\theta}}(s_{t+1}) - V_{\pi_{\theta}}(s_t)

Select actions from parametrized distribution family, e.g, Gaussian

Many version of PG formula:

Screen from GAE paper(arxiv.org/abs/1506.02438):

Which \(\Psi_{t}\) is suitable for continuous action spaces?

All of them!

A2C with Q-values

In discrete case we can just output all \(Q(s,a)\):

But we are interested only in \(Q\)-values for particular \(a_t\)!

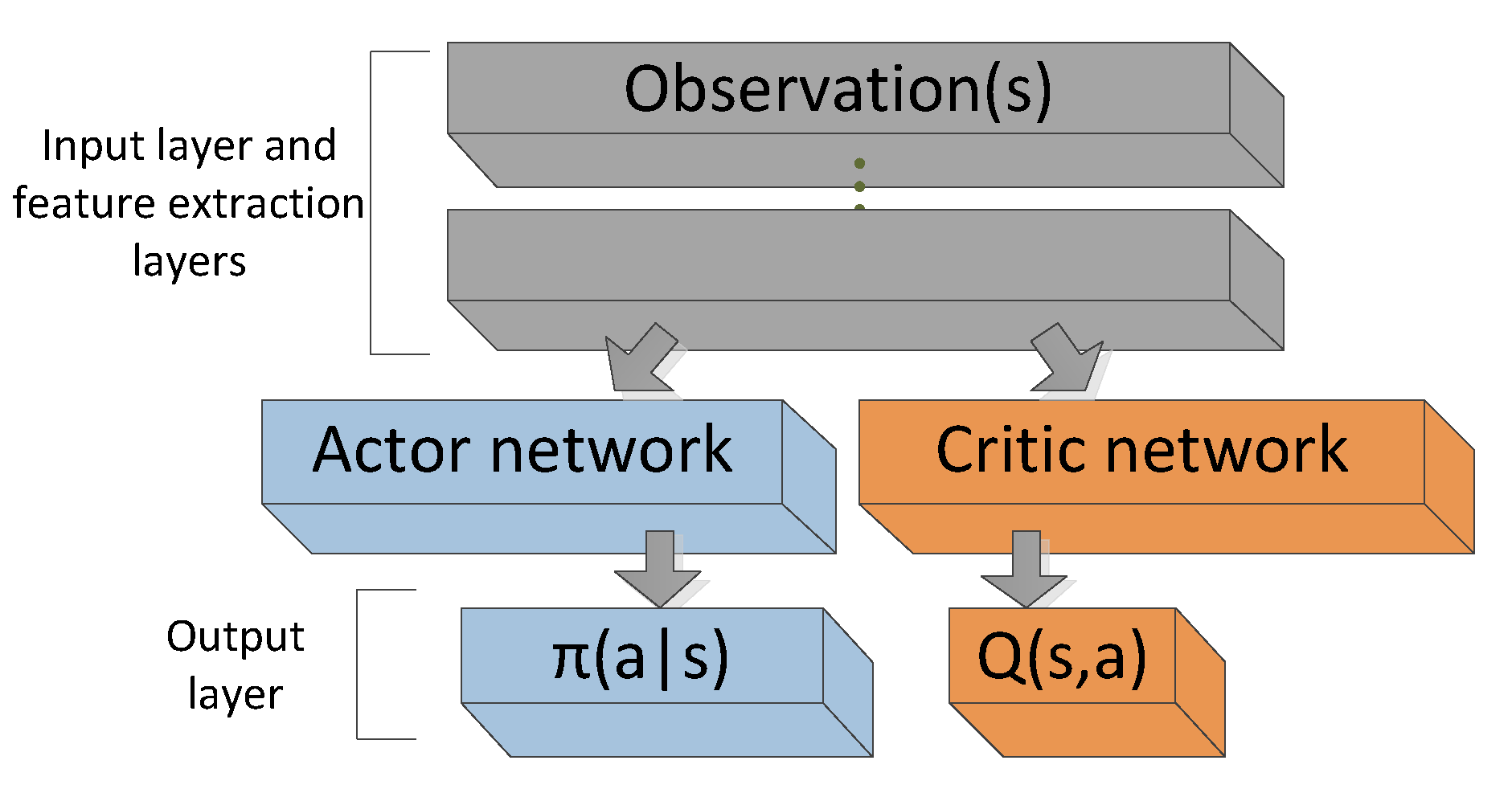
A2C: Q-values + Continuous Actions

Continuous case: Estimate \(Q\)-values only for the selected action \(a_t\)

Conclusions:

  • Explicit policy allows to omit the problem with \(argmax_{a}\) over all actions
  • PG theorem proofs that this is a correct algorithm

Continuous case: Estimate \(Q\)-values only for the selected action \(a_t\)

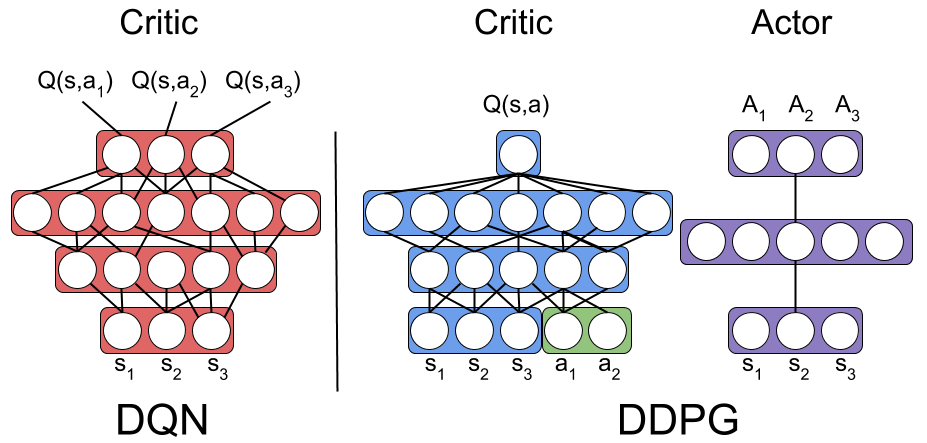
One problem: PG is still on-policy!

DPG: Intro

Idea:

  1. Learn Q-values off-policy with 1-step TD-updates
  2. Gradients \(\nabla_{a} Q_{\phi}(s,a)\) tell how to change the action \(a \sim \pi(s)\)  to increase \(Q\)-value
  3. Update actor with these gradients!

Problems:

  1. Can't flow gradients via sampled actions!
  2. Do we have any justifications for this?

Use deterministic policy ¯\_(ツ)_/¯

Yes! For deterministic policy :)

Deterministic Policy Gradients:

Now we can rewrite RL objective (Recall PG lecture): 

Lets start for new definitions:  

  • \(\rho_1(s)\): The initial distribution over states
  • \(\rho(s \rightarrow s', k, \mu)\): starting from \(s\), the visitation probability density at \(s'\) after moving k steps with policy \(\mu\)
  • \(\rho^{\mu}(s')\): Discounted state distribution, defined as: 
\textcolor{red}{\rho^{\mu}(s')} = \int_{\mathbb{S}} \sum^{\infty}_{k=0} \gamma^{k-1} \textcolor{green}{\rho_{1}(s)} \textcolor{blue}{\rho(s \rightarrow s',k, \mu)} ds
J(\mu_\theta) = \mathbb{E}_{\tau \sim \mu_{\theta}(\tau)} [ \sum\limits_t \gamma^{t} r(s_t, a_t)] = \int_{\mathbb{\tau}} p_{\mu_{\theta}}(\tau) \sum\limits_t \gamma^{t} r(s_t, a_t)\, d \tau
= \textcolor{red}{\int_{\mathbb{S}} \rho^{\mu_{\theta}}(s)} \int_{\mathbb{A}} \mu_{\theta}(s|a) r(s,a)\, da\,ds = \mathbb{E}_{\textcolor{red}{s \sim \rho^{\mu_{\theta}}}, a \sim \mu_{\theta}} [r(s_t, a_t)]

Deterministic Policy Gradients:

Deterministic Policy Gradient Theorem:

where, 

  • \(\rho_1(s)\): the initial distribution over states
  • \(\rho(s \rightarrow s', k, \mu)\): starting from \(s\), the visitation probability density at \(s'\) after moving k steps with policy \(\mu\)
  • \(\rho^{\mu}(s')\): Discounted state distribution, defined as: 
\textcolor{red}{\rho^{\mu}(s')} = \int_{\mathbb{S}} \sum^{\infty}_{k=1} \gamma^{k-1} \textcolor{green}{\rho_{1}(s)} \textcolor{blue}{\rho(s \rightarrow s',k, \mu)} ds
\nabla_{\theta} J(\mu_{\theta}) = \textcolor{red}{\int_{\mathbb{S}} \rho^{\mu}(s)} \nabla_{\theta} \mu_{\theta}(s) \nabla_a Q^{\mu}(s,a)|_{a=\mu_{\theta}(s)} \textcolor{red}{\,ds}
= \textcolor{red}{\mathbb{E}_{s \sim \rho^{\mu}}} [ \nabla_{\theta} \mu_{\theta}(s) \nabla_a Q^{\mu}(s,a)|_{a=\mu_{\theta}(s)} ]

Deterministic Policy Gradients:

TODO! Choose one of Two types of Explanation:

Var1:

  • DPG theorem proof

Var2:

  • PG theorem with "improper" discounted \(\rho^{\pi}(s)\) as it easier
  • Show part of DPG Theorem until we start telescoping 
  • Then DPG is similiar with PG only with integrals

 

DPG Proof V1

For more details see: DPG paper and supplementary materials

Notice that we also can rewrite \(J(\mu_{\theta})\) as:

J(\mu_\theta) = \mathbb{E}_{\tau \sim \mu_{\theta}(\tau)} [ \sum\limits_t \gamma^{t} r(s_t, a_t)] = \textcolor{green}{\int_{\mathbb{S}} p_1(s)} V^{\mu_{\theta}}(s)\, ds

And first we want to prove that:

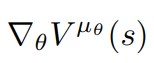
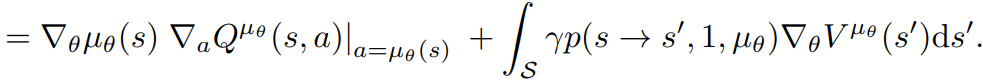
DPG at first step

expectation over s'

V-value at next step

DPG Proof V1

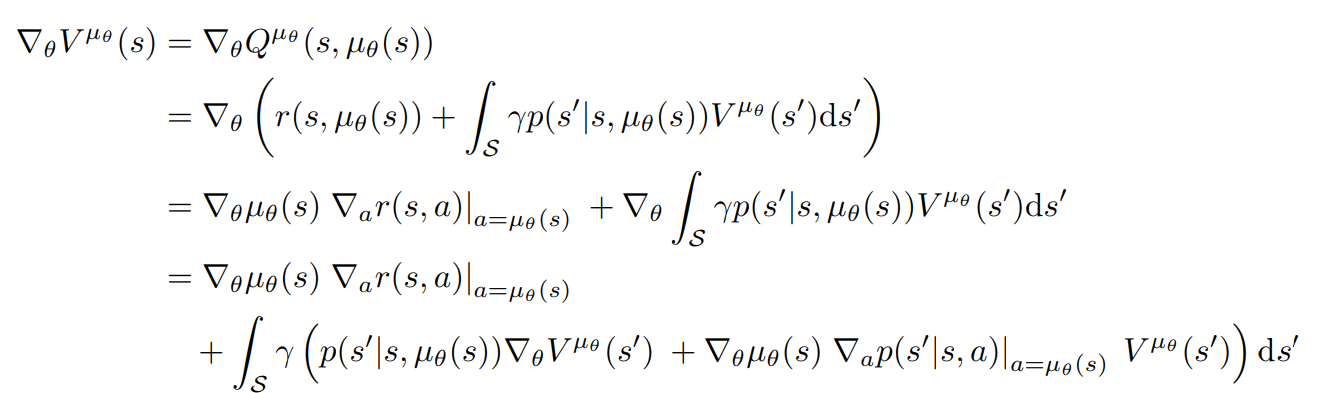
Leibniz integral rule:

swap grad and integral

same

same

DPG Proof V1

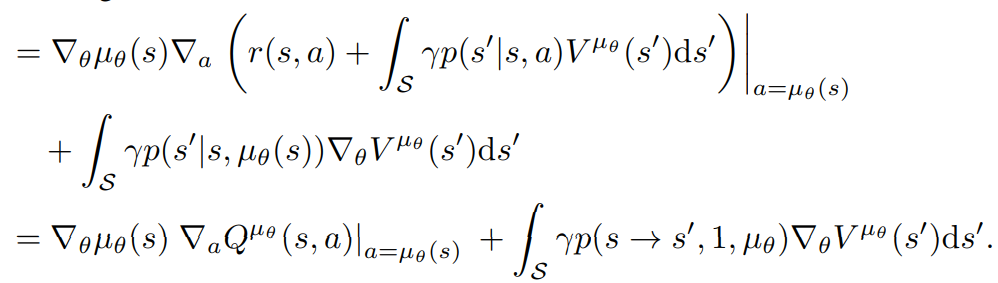
linearity of gradients and integration

By Q-value definition!

by definition of \(p(s \rightarrow s', k, \mu_{\theta})\)

Deterministic Policy Gradient V1

This is proven:

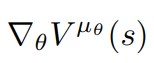
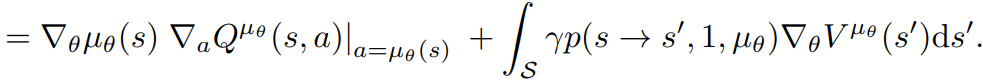
Now we can recursively iterate with this formula for all steps:

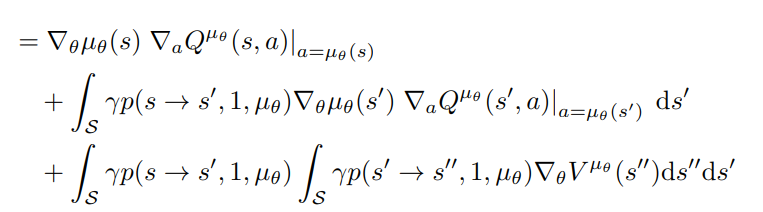
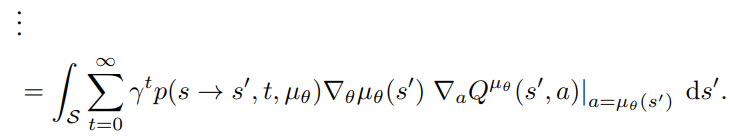
until all \(\nabla _{\theta}V^{\mu_{\theta}}\) are gone!

Deterministic Policy Gradient V1

Now return to:

And substitute \(\nabla_{\theta} V^{\mu_{\theta}}\) with our new formula:

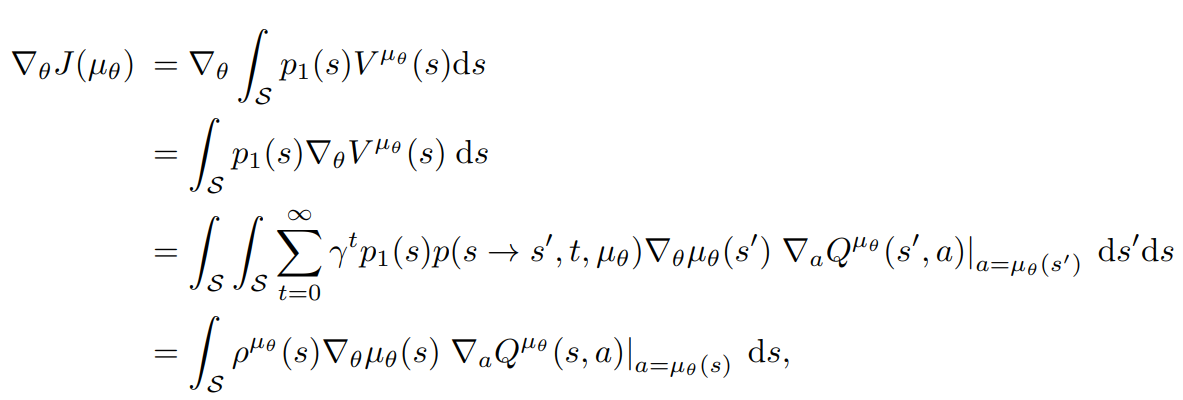
J(\mu_\theta) = \mathbb{E}_{\tau \sim \mu_{\theta}(\tau)} [ \sum\limits_t \gamma^{t} r(s_t, a_t)] = \textcolor{green}{\int_{\mathbb{S}} p_1(s)} V^{\mu_{\theta}}(s)\, ds

Leibniz integral rule

Fibini's theorem to swap integration order

\textcolor{red}{\rho^{\mu}(s')} = \int_{\mathbb{S}} \sum^{\infty}_{k=1} \gamma^{k-1} \textcolor{green}{\rho_{1}(s)} \textcolor{blue}{\rho(s \rightarrow s',k, \mu)} ds

Deterministic Policy Gradient:

Off-policy Policy Gradient theorem (arxiv.org/abs/1205.4839):

We can learn DPG off-policy:

  • DPG version of Off-Policy PG Theorem allows to ignore importance sampling correction
  • Learning Q-function with 1-step TD-learning allows to learn critic off-policy

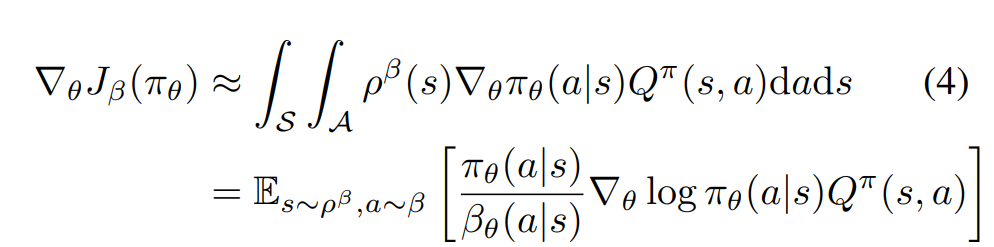
Imporance sampling

recall TRPO, PPO derviations...

Deep Deterministic Policy Gradient

Mods inspired by DQN: 

  • Add noise(Ornstein-Uhlenbeck or Gaussian) to the sampling policy:

   

  • Replay Buffer as in DQN
  • Separate "deep" networks for Actor and Critic
  • Target Actor and target Critic 
  • Update target networks with moving average:

Lets combine DPG with Deep Learning and create DDPG!

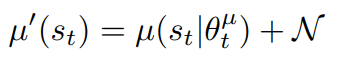
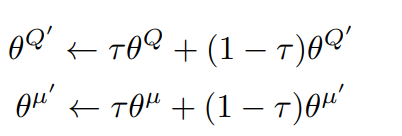
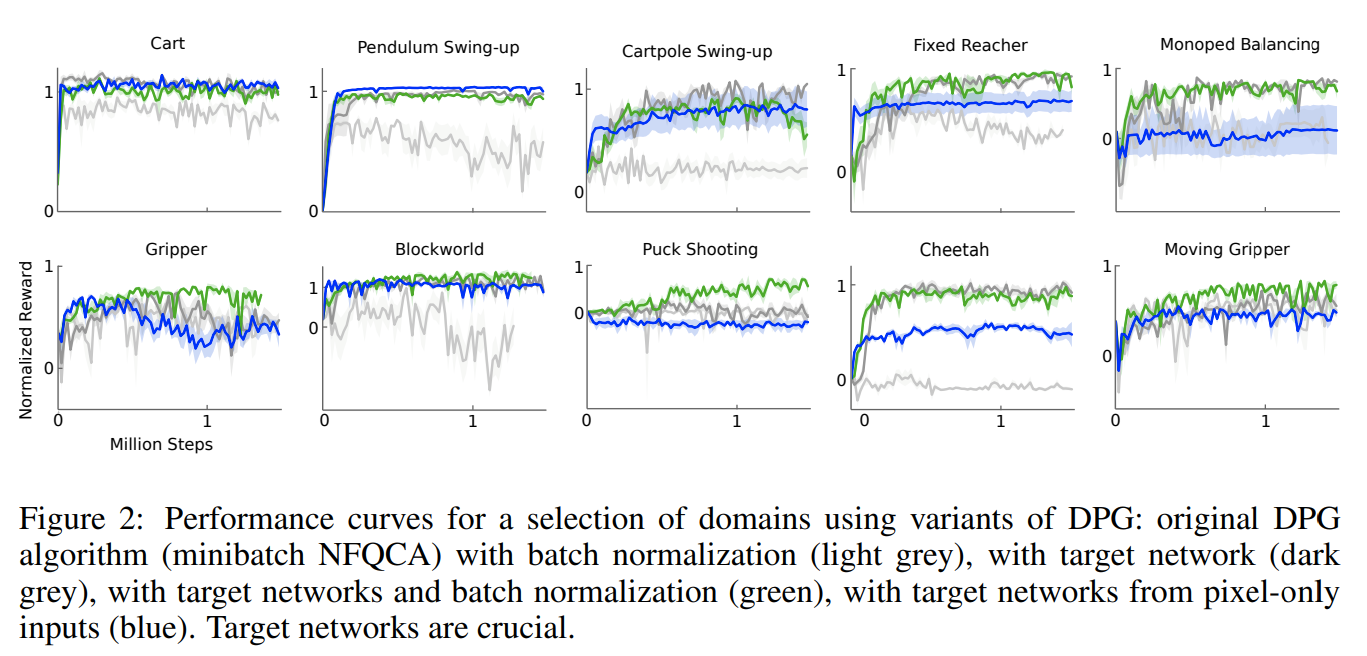
DDPG Results

Twin-Delayed DPG

DDPG has many problems! Lets try to fix them!

Fix #1

Clipped Double Q-learning [ this is "twin" part ]:

  • Train two Critic networks:

 

 

 

  • Fight overestimation bias by taking minimum of the two targets:

 

 

 

DDPG has many problems! Lets try to fix them!

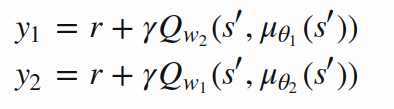
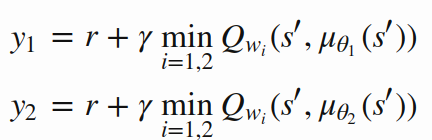
Twin-Delayed DPG

DDPG has many problems! Lets try to fix them!

Fix #2
Delayed update of Target and Policy Networks:

  • Problem: policy updates is poor if value estimates are inaccurate
  • Update Target Networks and Actor less frequently than Critic

 

 

 

DDPG has many problems! Lets try to fix them!

From author's code of TD3:

Twin-Delayed DPG

DDPG has many problems! Lets try to fix them!

Fix #3
Target Policy Smoothing [ No reference in the name :( ]

  • Problem: Deterministic policies can overfit to narrow peaks/fluctuations in the value function
  • Add noise to the Traget Policy's action to prevent this:

 

 

 

DDPG has many problems! Lets try to fix them!

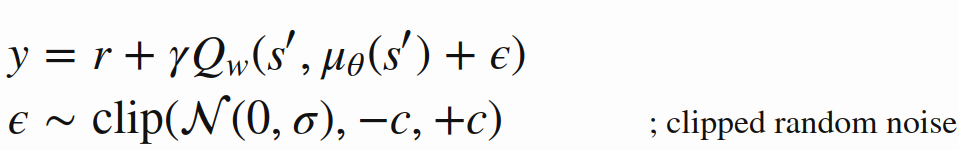
Twin-Delayed DPG

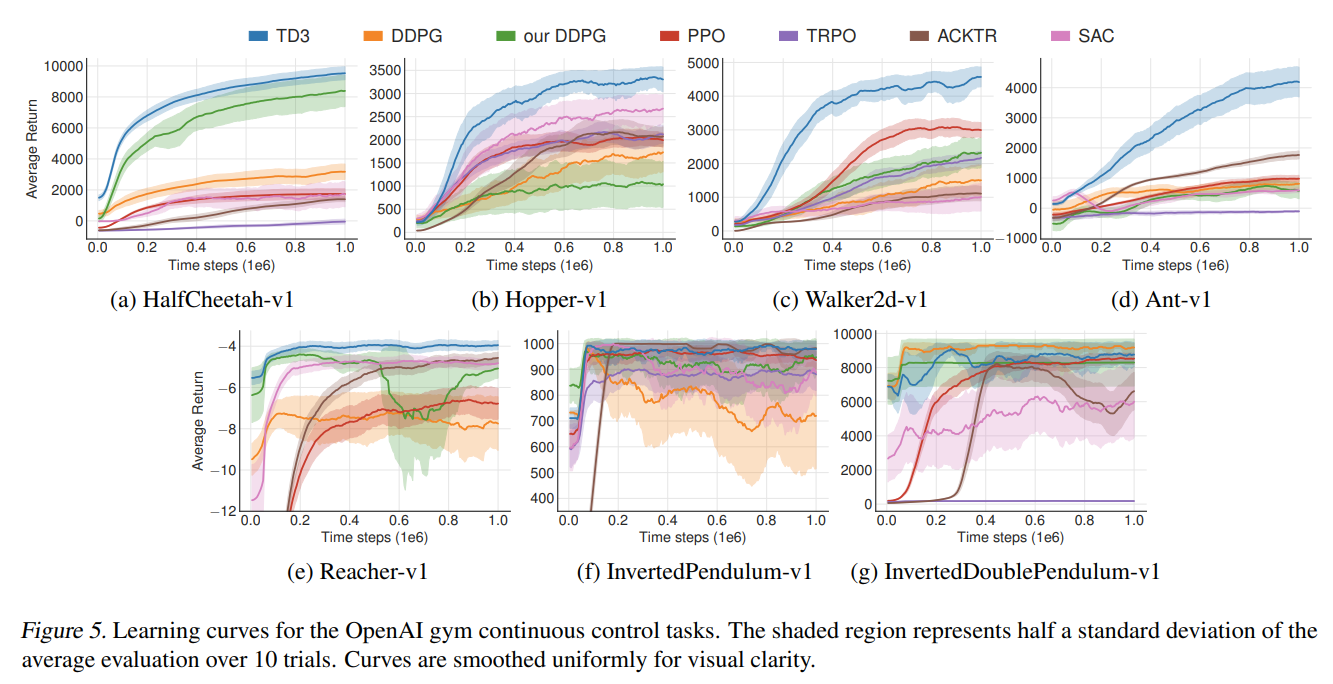
TD3: Results

Maximum Entropy RL

Max Entropy Objective:

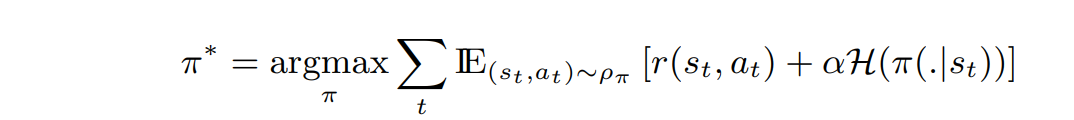
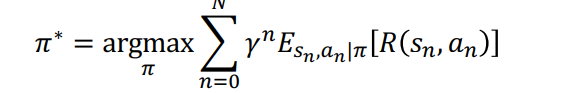
Regular RL Objective:

Maximum Entropy RL

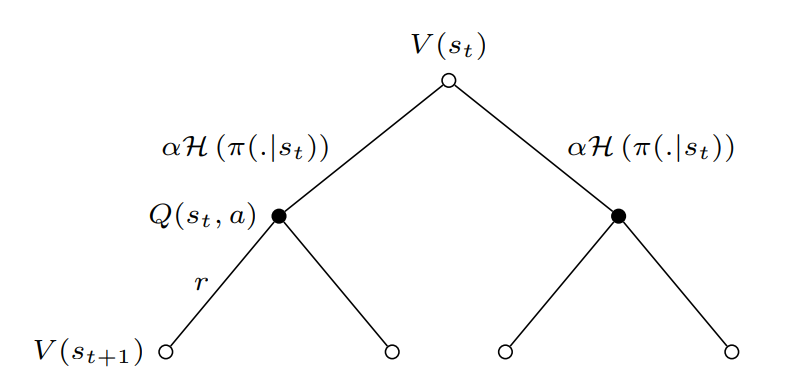
Backup Diagram:

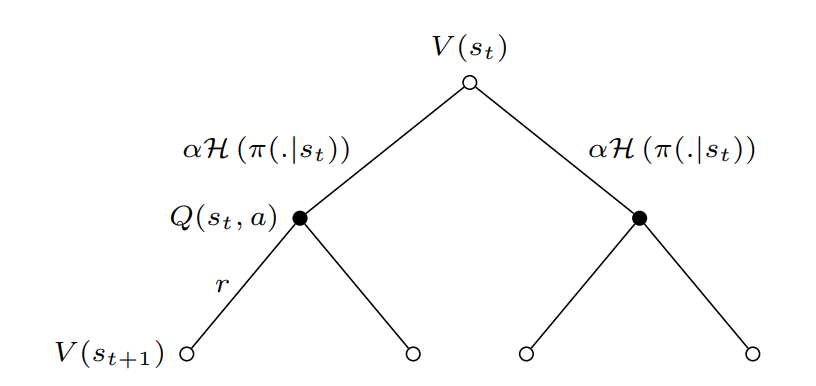
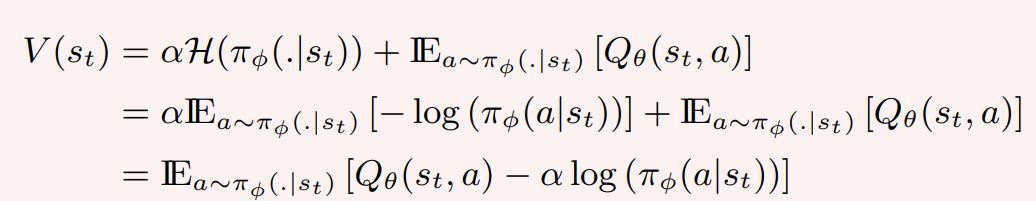
Add \(soft\) for every value function

Maximum Entropy RL

Maximum Entropy Bellman Operator: 

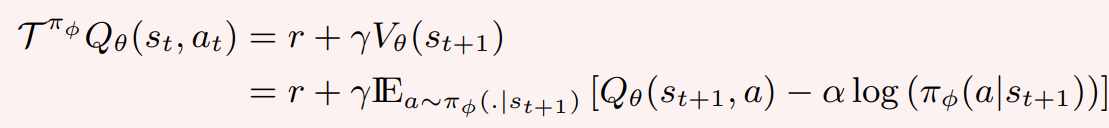
Maximum Entropy RL

Why softmax over \(Q\)-values imporves policy?

Soft-PI: Intuition for Softmax

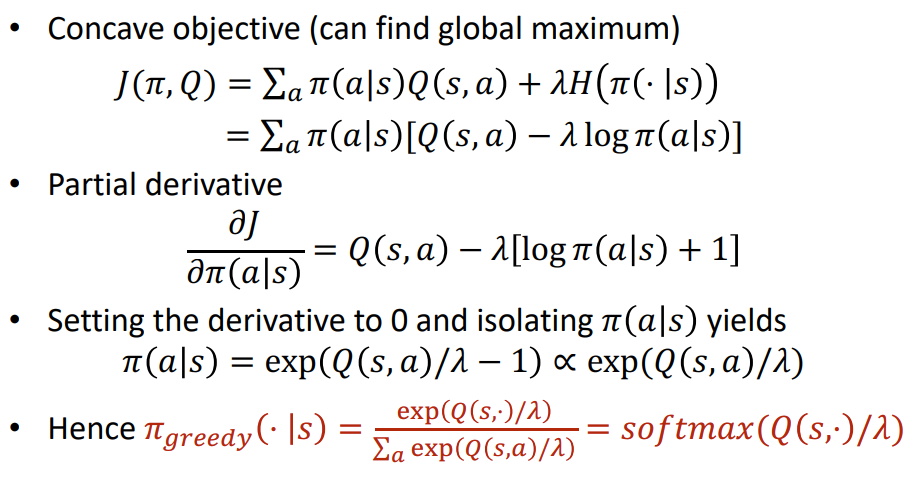
Concave objective (can find global maximum): 

Take partial derivative w.t.r. to the action probability: 

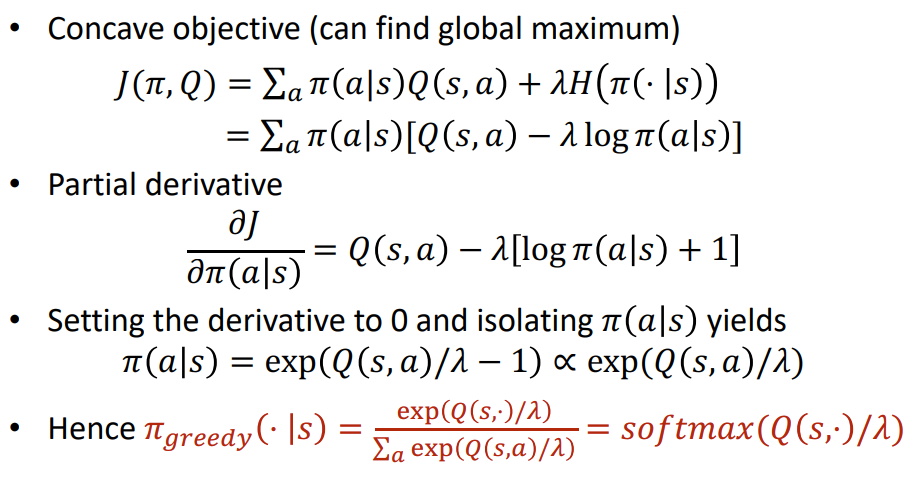
Set derivative to 0 and find maximum: 

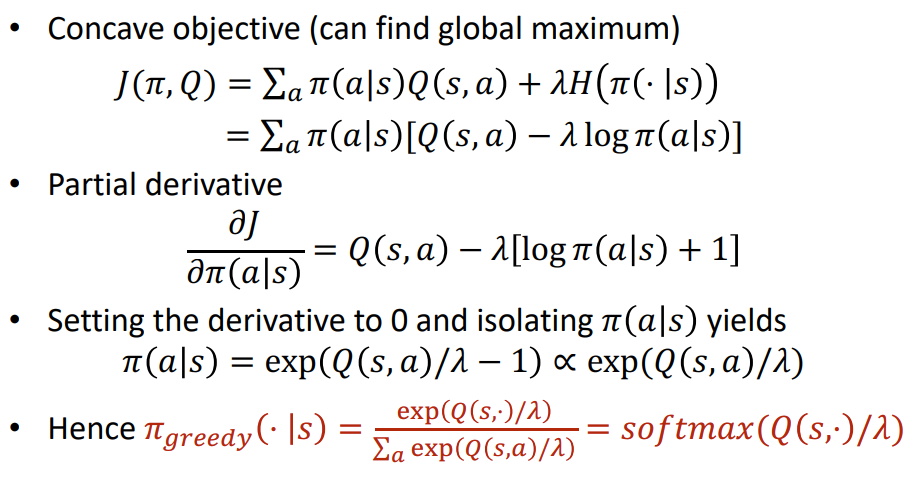
The only problem \(\pi(a|s)\) is a probability distribution:

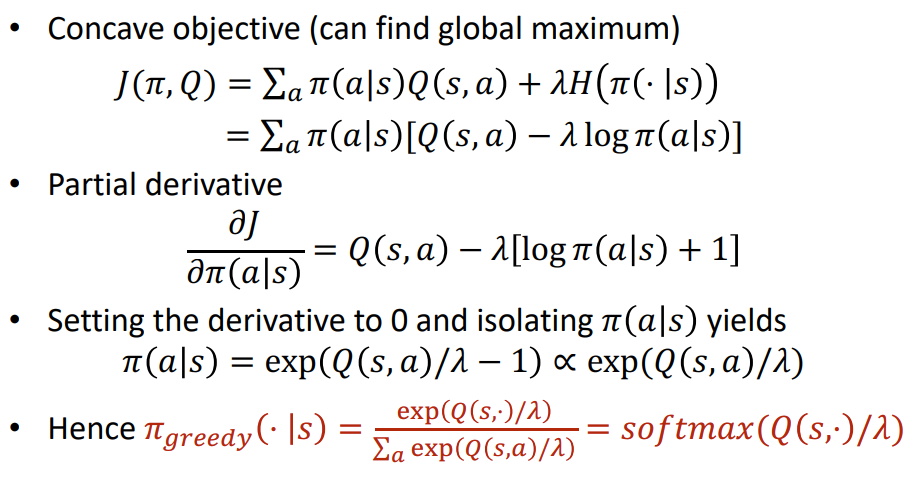
Policy Improvement: Proof

Policy Improvement: Proof

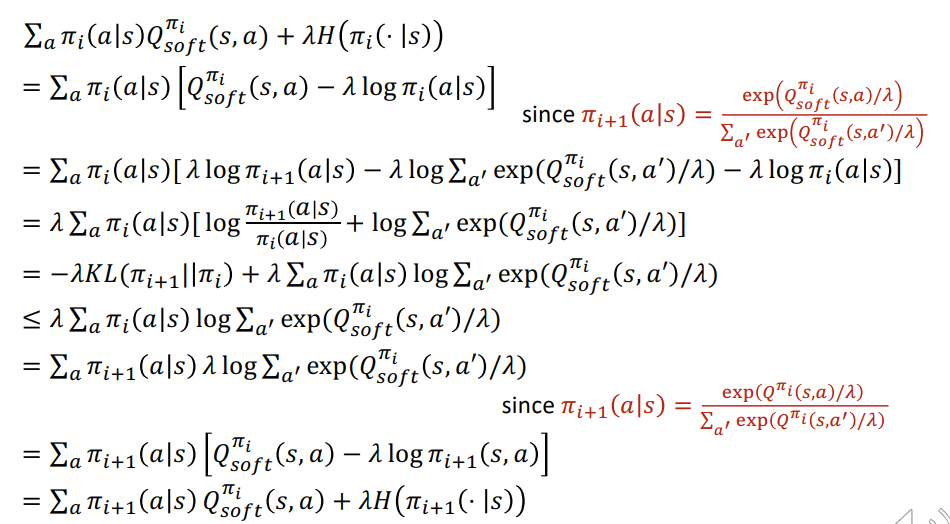
Policy Improvement: Proof

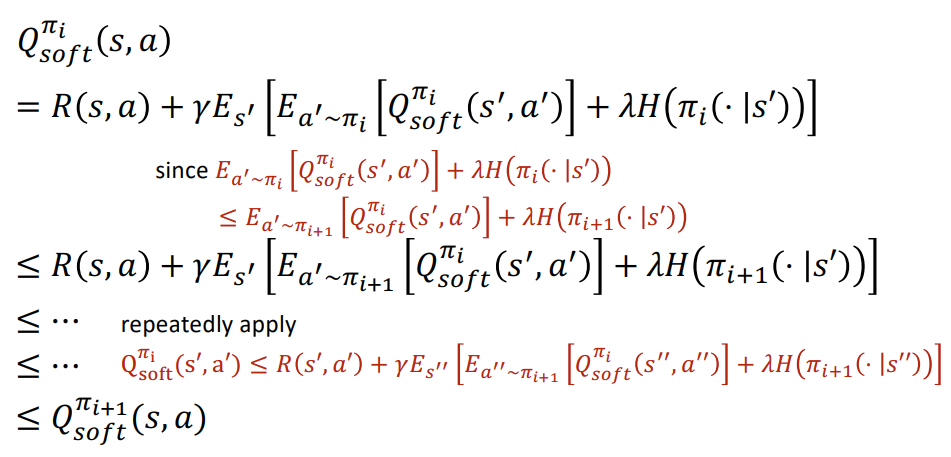
Soft-Actor Critic

Policy Evaluation doesn't need to change:

Lets upgrade Soft Policy iteration for continuous action space!

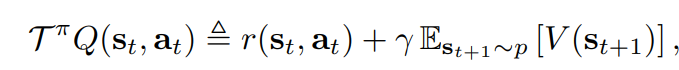
Policy Improvement step for continuous policy:

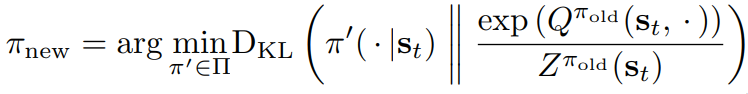
Soft-Actor Critic

Critic approximate Policy Evaluation. Trains with MSE:

Actor apporximate Policy Improvement. Trains with the following loss:

J_{Q}(\theta) = \mathbb{E}_{(s_t,a_t) \sim \mathbb{D}} \Biggl[ \frac{1}{2} (Q^{\theta}_{soft}(s_t,a_t)- \hat{Q}_{soft}(s_t,a_t))^2 \Biggr]
\hat{Q}_{soft}(s_t,a_t) = r(s_t,a_t) + \gamma \mathbb{E}_{s_{t+1}, a_{t+1}} [ Q^{\bar{\theta}}_{soft}(s_{t+1},a_{t+1}) - log\,\pi_{\phi}(a_{t+1}|s_{t+1}) ]

where:

J_{\pi}(\phi) = \mathbb{E}_{(s_t,a_t) \sim \mathbb{D}} [ log\, \pi_{\phi}(a_t| s_t) - Q^{\theta}_{soft}(s_t, a_t) ]

SAC evolution:

Soft-Actor Critic

Implementation Details: 

  • Reparametrization trick for policy:
    • Therefore actor loss becomes:

 

 

  • Twin Critics for Q-value (like in TD3)
  • Moving average update for targets (like in TD3, DDPG)
  • tanh squashing for outputs: \(a_t = tanh(f_{\phi}(\epsilon_t; s_t)) \)

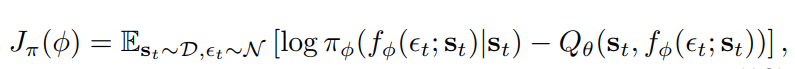
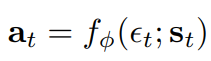
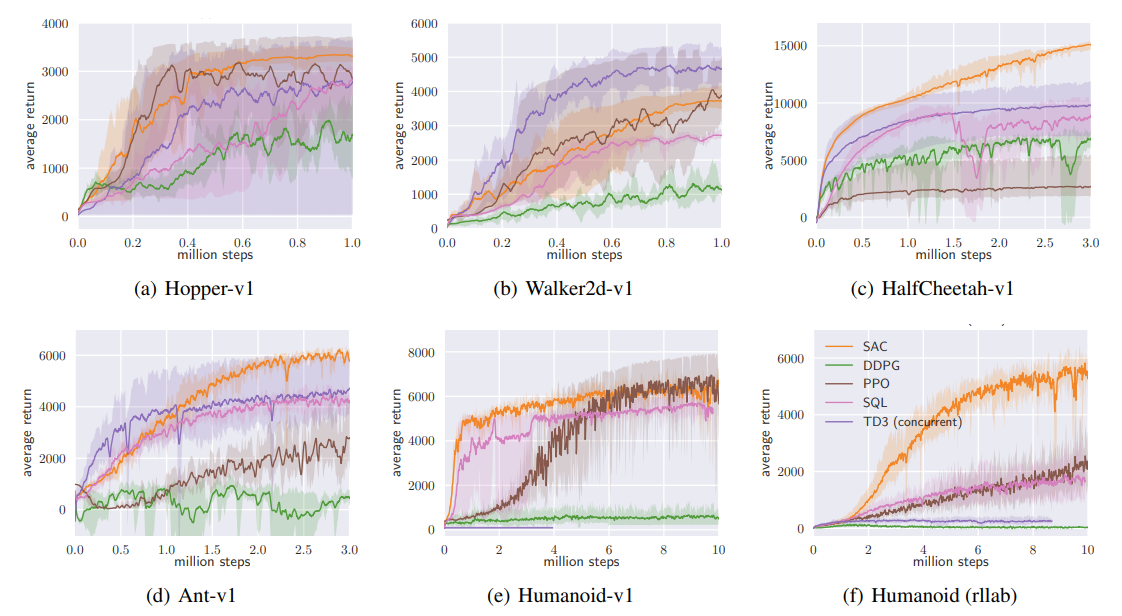
Soft-Actor Critic: Results

Conclusion:

For environments with continual action spaces start from either TD3 or SAC

TD3 graph: TD3 > SAC

SAC graph: SAC > TD3

Thank you for your attention!

08 - Continuous Control

By supergriver

08 - Continuous Control

  • 328

More from supergriver