Aztec's zk\(^2\)-Rollup
Suyash Bagad
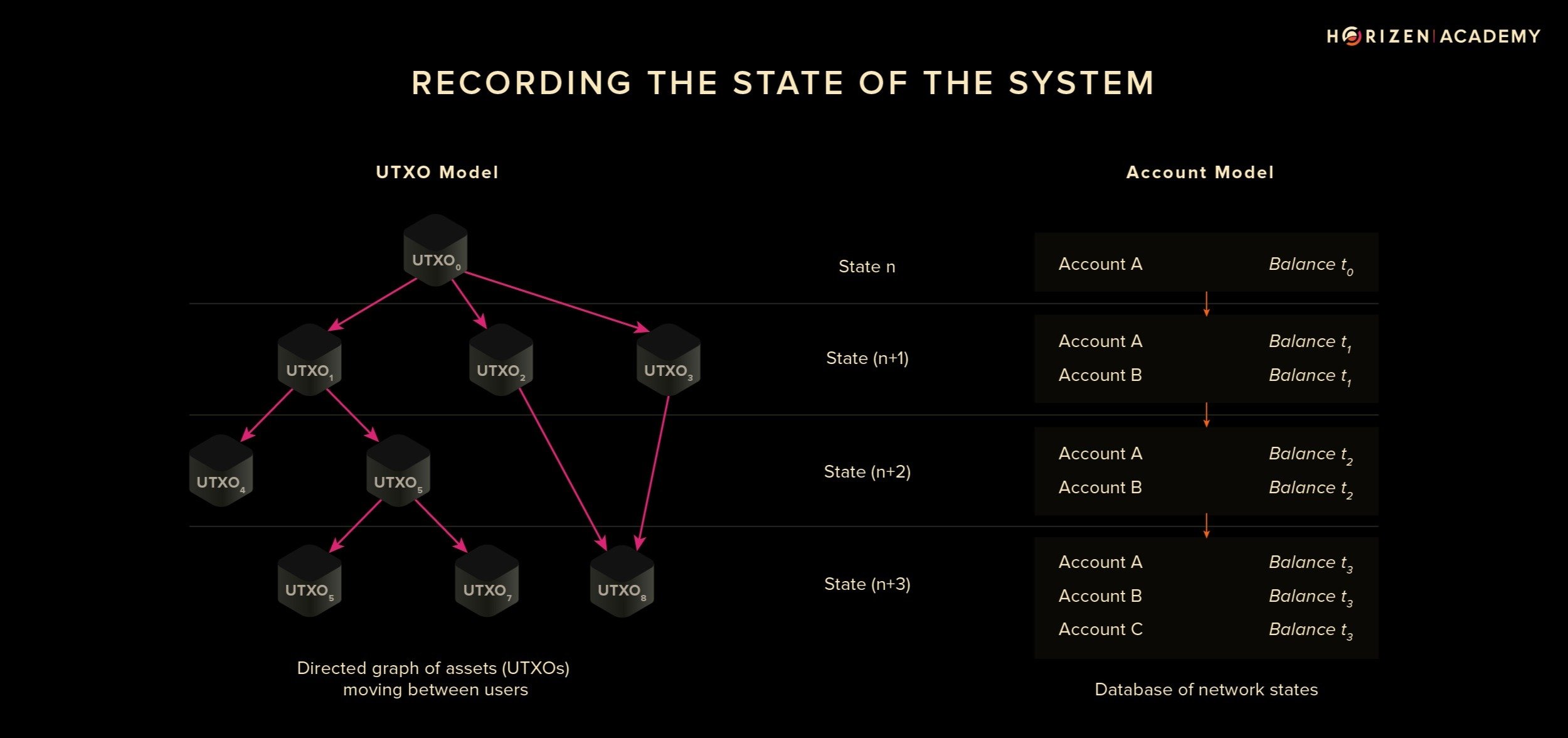
UTXO vs Account
Aztec Model

20

Bob

Alice
Open account

\(\texttt{bob}\)

\(\texttt{alice}\)

8


2



10


10

0.5


1.5



18


2
10

Shield
Rollup Contract


Account UTXO
Value UTXO
Private sends
\(\text{zkETH}=8.5\)
\(\text{zkDAI}=18\)
\(\text{zkETH}=1.5\)
\(\text{zkDAI}=2\)
Withdraw
\(0\)
1.5

Aztec Notes
- Account balances are calculated by adding up the available UTXOs
- UTXOs are called as notes: \(\textcolor{orange}{\textsf{Account}}\) notes and \(\textcolor{violet}{\textsf{Value}}\) notes
- State transition in UTXO model is tricky
- A user creates an account on zk.money using an alias and a nonce \(n \in \mathbb{Z}^{32}_2\)
- We compute an account identifier as:
- Account information is stored in account notes
Account PK
Account id
Spending PK1

\(a_{\text{id}} \ \in \ \mathbb{Z}_2^{32}\)
\(S_1 \ \in \ \mathbb{G}_1\)
\(A \ \in \ \mathbb{G}_1\)
Account PK
Account id
Spending PK2

\(a_{\text{id}} \ \in \ \mathbb{Z}_2^{32}\)
\(S_2 \ \in \ \mathbb{G}\)
\(A \ \in \ \mathbb{G}_1\)
\(a_{\text{id}} \coloneqq \left( n \ \| \ H_{B}\left(\texttt{suyashbagad}\right)[ \ 0 : 224 \ ]\right) \in \mathbb{Z}^{256}_2\)
- Spending keys are used for signing transactions
Aztec Notes
- Aztec uses value notes as a basis for private transactions on Ethereum

Value
Asset id
Nonce

Owner
Secret
\(a \ \in \ \mathbb{Z}_2^{32}\)
\(A \ \in \ \mathbb{G}_1\)
\(n \ \in \ \mathbb{Z}_2^{32}\)
\(v \ \in \ \mathbb{F}_q\)
\(s \ \in \ \mathbb{F}_q\)
- A value note is given as: \(\mathcal{V} = \{a, v, n, \mathcal{O}, s\}\)
- The nonce here is same as the one used in an account note
- A note incorporates the on-chain identity (i.e. account PK) of its owner
- The secret \(s\) is the hiding factor in computing Pedersen commitment to a note:
Demo
- Creating an account using alias \(\texttt{arcanatest}\)
- Shielding \(0.1\) ETH, sending some ETH privately \(\texttt{trial}\rightarrow \texttt{test}\)
- Client-side proof generation: \(n=32000\) circuit size
- Plonk proof data: nullifiers and data entry
- Before delving into circuits, we'll discuss some prelims
Arithmetic Circuit
- A typical computational problem: find solutions to the equation (i.e. \(\textsf{stmt}\))
\(x_1^2 \cdot x_2 + x_1 + 1 = 22\)
- Witness: \(w \equiv (x_1=3, x_2=2)\), public inputs: \(\ell \equiv (c=1, z=22)\)
- I can convince you that I know a solution \(w\) to \(\{\textsf{stmt}, \ell\}\) without revealing \(w\)
- PLONK: Circuit size: \(n=4\), prover: \(\mathcal{O}(n\cdot\text{log}n)\), proof size and verifier: \(\mathcal{O}(1)\)
Data Tree
- \(\mathbb{D}\) is size \(2^{32}\) Merkle tree which supports batch updates
- Contains commitments to all account and value notes ever created in Aztec
- Suppose we wish to add \(\mathcal{A}_1, \mathcal{A}_2, \mathcal{V}_1, \mathcal{V}_2\) to \(\mathbb{D}\)
Data Tree
- Old data root: \(D_{\text{old}},\)
\(\mathfrak{C}(\mathcal{A}_1)\)
\(\mathfrak{C}(\mathcal{A}_2)\)
\(\mathfrak{C}(\mathcal{V}_1)\)
\(\mathfrak{C}(\mathcal{V}_2)\)
\(D\)
New data root: \(D_{\text{new}}\)
Data Tree
- Old data root: \(D_{\text{old}},\)
- With subtree root \(S\) and the partial proof \(\{h_1, h_2\}\), we can verify:
\(\mathfrak{C}(\mathcal{A}_1)\)
\(\mathfrak{C}(\mathcal{A}_2)\)
\(\mathfrak{C}(\mathcal{V}_1)\)
\(\mathfrak{C}(\mathcal{V}_2)\)
\(D\)
New data root: \(D_{\text{new}}\)
\(S\)
\(h_1\)
\(h_2\)
\(D_{\text{new}} \stackrel{?}{=} H\left(h_2, H(S, h_1)\right)\)
Nullifier Tree
- \(\mathbb{N}\) is size \(2^{256}\) sparse Merkle tree which supports non-membership proofs
- To prove that a note is unspent, we need to give a non-membership proof
- Suppose we have \(16\) leaf values \(\{A, B, \dots, P\}\) s.t. \(\text{idx}(A) = 1\) and so on
- To prove \(J \notin \mathbb{T}\), a membership proof \((10, \phi, \pi_{\text{merkle}})\) suffices!
\(A\)
\(F\)
\(N\)
Account Circuit
- Let's look at an example of account migration
- New account notes must have same alias but different nonce
- Need to track the old and new account notes!
- Check if the old notes actually exist in the data tree: \(\mathfrak{C}(\mathcal{A}_{1, \text{old}}), \ \mathfrak{C}(\mathcal{A}_{2, \text{old}}) \in \mathbb{D}\)
- Add old note nullifiers to the nullifier tree: \( \mathbb{N} \longleftarrow \mathfrak{N}(a_{\text{id, old}})\)
- Add new note commitments to the data tree: \( \mathbb{D} \longleftarrow \left\{ \mathfrak{C}(\mathcal{A}_{1, \text{new}}), \ \mathfrak{C}(\mathcal{A}_{2, \text{new}}) \right\}\)
- Check the validity of signature \(\sigma(a_{\text{id, old}}, A_{\text{old}}, A_{\text{new}}, S_{1, \text{old}}, S_{2, \text{old}})\)
- If not migrating, set \(n_{\text{new}} = n_{\text{old}}\) and check \(A_{\text{old}} = A_{\text{new}}\)

\(a_{\text{id, new}}\)
\(S_{1, {\text{new}}} \)
\(A_{\text{new}} \)

\(a_{\text{id, old}}\)
\(S_{2, {\text{new}}} \)
\(A_{\text{new}} \)
\(\mathcal{A}_{2, \text{new}}\)
\(\mathcal{A}_{1, \text{new}}\)

\(a_{\text{id, old}}\)
\(S_{1, {\text{old}}} \)
\(A_{\text{old}} \)
\(\mathcal{A}_{1, \text{old}}\)

\(a_{\text{id, old}}\)
\(S_{2, {\text{old}}} \)
\(A_{\text{old}} \)
\(\mathcal{A}_{2, \text{old}}\)
Join-Split Circuit
- A join-split transaction spends two input notes and creates two new output notes
\(\mathcal{V}^{\text{in}}_{1} = \{a^{\text{in}}_1, v^{\text{in}}_1, n^{\text{in}}_1, A^{\text{in}}_1, s^{\text{in}}_1 \}\)
\(\mathcal{V}^{\text{in}}_{2} = \{a^{\text{in}}_2, v^{\text{in}}_2, n^{\text{in}}_2, A^{\text{in}}_2, s^{\text{in}}_2 \}\)
\(\mathcal{V}^{\text{out}}_{1} = \{a^{\text{out}}_1, v^{\text{out}}_1, n^{\text{out}}_1, A^{\text{out}}_1, s^{\text{out}}_1 \}\)
\(\mathcal{V}^{\text{out}}_{2} = \{a^{\text{out}}_2, v^{\text{out}}_2, n^{\text{out}}_2, A^{\text{out}}_2, s^{\text{out}}_2 \}\)
- A join-split transaction must obey the following:
- Asset ids must match: \(a_1^{\text{in}} = a_2^{\text{in}} = a_1^{\text{out}} = a_2^{\text{out}} =: a\)
- Input note owners must match: \(A_{1}^{\text{in}} = A_{2}^{\text{in}}\)
- Input note nonces match: \(n^{\text{in}}_1 = n^{\text{in}}_2 = n\)
- Amounts are balanced: \(v^{\text{in}}_1 + v^{\text{in}}_2 = v^{\text{out}}_1 + v^{\text{out}}_2 + \text{tx\_fee}\)
- Range constraints: \(\text{tx\_fee} \le 2^{242}, a \le 2^{32}\)
Join-Split Circuit
- A join-split transaction spends two input notes and creates two new output notes
\(\mathcal{V}^{\text{in}}_{1} = \{a^{\text{in}}_1, v^{\text{in}}_1, n^{\text{in}}_1, A^{\text{in}}_1, s^{\text{in}}_1 \}\)
\(\mathcal{V}^{\text{in}}_{2} = \{a^{\text{in}}_2, v^{\text{in}}_2, n^{\text{in}}_2, A^{\text{in}}_2, s^{\text{in}}_2 \}\)
\(\mathcal{V}^{\text{out}}_{1} = \{a^{\text{out}}_1, v^{\text{out}}_1, n^{\text{out}}_1, A^{\text{out}}_1, s^{\text{out}}_1 \}\)
\(\mathcal{V}^{\text{out}}_{2} = \{a^{\text{out}}_2, v^{\text{out}}_2, n^{\text{out}}_2, A^{\text{out}}_2, s^{\text{out}}_2 \}\)
- State transition constraints
- Input notes must be present in the data tree: \( \mathfrak{C}(\mathcal{V}_{1}^{\text{in}}), \mathfrak{C}(\mathcal{V}_{2}^{\text{in}}) \in \mathbb{D}\)
- Input notes are not already spent: \( \mathfrak{N}(\mathcal{V}_{1}^{\text{in}}), \mathfrak{N}(\mathcal{V}_{2}^{\text{in}}) \notin \mathbb{N}\)
- Nullify the input notes to avoid double-spending: \(\mathbb{N} \longleftarrow \mathfrak{N}(\mathcal{V}_{1}^{\text{in}}), \mathfrak{N}(\mathcal{V}_{2}^{\text{in}})\)
- Output notes are added to the data tree: \(\mathbb{D} \longleftarrow \mathfrak{C}(\mathcal{V}_{1}^{\text{out}}), \mathfrak{C}(\mathcal{V}_{2}^{\text{out}})\)
Recursive Proof Verification
- A Plonk proof \(\pi\) is verified by checking equality of polynomial evaluations
\(\pi = \bigg\{\underbrace{[a]_1, [b]_1, [c]_1, [z]_1, [t_0]_1, [t_1]_1, [t_2]_1, [W_{\mathfrak{z}}]_1, [W_{\mathfrak{z\omega}}]_1}_{\mathbb{G}_1^{2w + 3}}, \ \underbrace{\bar{a}, \bar{b}, \bar{c}, \bar{z}_{\omega}, \bar{s}_{\sigma_1}, \bar{s}_{\sigma_2}}_{\mathbb{F}_p^{2w}} \bigg\}\)
\(W_{\mathfrak{z}}(x) \cdot (x - \mathfrak{z}) = F_1(x) - F_1(\mathfrak{z})\)
\(W_{\mathfrak{z\omega}}(x) \cdot (x - \mathfrak{z}\omega) = F_2(x) - F_2(\mathfrak{z}\omega)\)
\(W_{\mathfrak{z}}(x) \cdot (x - \mathfrak{z}) + u \cdot (W_{\mathfrak{z\omega}}(x) \cdot (x - \mathfrak{z}\omega))= F_1(x) - F_1(\mathfrak{z}) + u \cdot (F_2(x) - F_2(\mathfrak{z}\omega))\)
Recursive Proof Verification
- A Plonk proof \(\pi\) is verified by checking equality of polynomial evaluations
\(\pi = \bigg\{\underbrace{[a]_1, [b]_1, [c]_1, [z]_1, [t_0]_1, [t_1]_1, [t_2]_1, [W_{\mathfrak{z}}]_1, [W_{\mathfrak{z\omega}}]_1}_{\mathbb{G}_1^{2w + 3}}, \ \underbrace{\bar{a}, \bar{b}, \bar{c}, \bar{z}_{\omega}, \bar{s}_{\sigma_1}, \bar{s}_{\sigma_2}}_{\mathbb{F}_p^{2w}} \bigg\}\)
\(W_{\mathfrak{z}}(x) \cdot (x - \mathfrak{z}) = F_1(x) - F_1(\mathfrak{z})\)
\(W_{\mathfrak{z\omega}}(x) \cdot (x - \mathfrak{z}\omega) = F_2(x) - F_2(\mathfrak{z}\omega)\)
\(W_{\mathfrak{z}}(x) \cdot (x - \mathfrak{z}) + u \cdot (W_{\mathfrak{z\omega}}(x) \cdot (x - \mathfrak{z}\omega))= F_1(x) - F_1(\mathfrak{z}) + u \cdot (F_2(x) - F_2(\mathfrak{z}\omega))\)
\(\underbrace{\left(W_{\mathfrak{z}}(x) + uW_{\mathfrak{z\omega}}(x)\right)}_{P_0} \cdot x = \underbrace{\left(\mathfrak{z}W_{\mathfrak{z}}(x) + u\mathfrak{z}\omega W_{\mathfrak{z\omega}}(x)) + F(x) - E\right)}_{P_1}\)
\(P_0 \cdot x \stackrel{?}{=} P_1\)
Recursive Proof Verification
- Suppose we have \(n\) Plonk proofs \((\pi_1, \pi_2, \dots, \pi_n)\) with verification equations:
\(P_0^{(i)} \cdot x \stackrel{?}{=} P_1^{(i)} \quad \forall i \in [n]\)
\(\left(P_0^{(1)} + qP_0^{(2)} + \dots + q^{n-1}P_0^{(n)}\right) \cdot x \stackrel{?}{=} \left(P_1^{(1)} + qP_1^{(2)} \dots + q^{n-1}P_1^{(n)}\right)\)
- A single pairing is \(\approx 300\) times costlier than a scalar multiplication
- Using recursive verification, we can verify any number of Plonk proofs using a single pairing
- Too good to be true? The circuit size presents a practical constraint on the number of proofs to be rolled up
- Failure of the recursive check implies at least one of the \(n\) proofs is wrong
DeFi Bridge
\(v^{\text{in}}_1 = 1\)
\(A = \texttt{0xF5C...17}\)
\(n = 15, s = \texttt{0x8C...2}\)

\(v^{\text{in}}_2 = 0.5\)
\(A = \texttt{0xF5C...17}\)
\(n = 15, s = \texttt{0x8C...2}\)

\(v^{\text{out}}_1 = 4500\)
\(A = \texttt{0xF5C...17}\)
\(n = 15, s = \texttt{0x8C...2}\)

\(v^{\text{out}}_2 = 0.15\)
\(A = \texttt{0xF5C...17}\)
\(n = 15, s = \texttt{0x8C...2}\)

DeFi Bridge
\(v^{\text{in}}_1 = 1\)
\(A = \texttt{0xF5C...17}\)
\(n = 15, s = \texttt{0x8C...2}\)

\(v^{\text{in}}_2 = 0.5\)
\(A = \texttt{0xF5C...17}\)
\(n = 15, s = \texttt{0x8C...2}\)

\(v^{\text{out}}_1 = 4500\)
\(A = \texttt{0xF5C...17}\)
\(n = 15, s = \texttt{0x8C...2}\)

\(v^{\text{out}}_2 = 0.15\)
\(A = \texttt{0xF5C...17}\)
\(n = 15, s = \texttt{0x8C...2}\)

\(d = 1.5\)
\(n_d = 4\)
\(P = H(A, n, s)\)

\(\texttt{DeFi Deposit}\)
\(\texttt{DeFi Claim}\)
\(\texttt{Claim Note}\)
\(v_1 = 0.4\)

\(v_2 = 0.8\)

\(d_1 = 1.2\)

\(v_3 = 1\)

\(v_4 = 0.1\)

\(d_2 = 1.1\)

\(v_5 = 0.05\)

\(v_6 = 0.15\)

\(d_3 = 0.2\)

\(v_7 = 0.3\)

\(v_8 = 0.1\)

\(d_4 = 0.4\)

\(v_9 = 0.2\)

\(v_{10} = 0.6\)

\(d_5 = 0.8\)

\(d_{\text{in}} = 3.7\)
\(n_d = 4\)

\(\texttt{in}\)
\(\texttt{out}\)
\(v_{\text{out}, 1} = 11,100\)
\(v_{\text{out}, 2} = 0.37\)



\(+\)
\(\texttt{DeFi Interaction Note}\)
\(v_1 = 3600\)

\(v_2 = 0.12\)

\(v_3 = 3300\)

\(v_4 = 0.11\)

\(v_5 = 600\)

\(v_6 = 0.02\)

\(v_7 = 1200\)

\(v_8 = 0.04\)

\(v_9 = 2400\)

\(v_{10} = 0.08\)

DeFi Bridge
Takeaways
- Aztec uses UTXO model (recall Hermez was account-based)
- Modern zkSNARKs are very powerful
- Allow one to prove complicated statements at low costs
- DSLs like Noir and Cairo make it easy for developers to write circuits
- No need to understand the moon-math to build apps
- Privacy at low costs for decentralised finance, NFTs, DAOs
- Aztec connect supports any application that can be modelled as async swap
- Single rollup provider as of today, will take time to decentralise
Aztec zk-zk-Rollup
By Suyash Bagad
Aztec zk-zk-Rollup
- 290



