Plookup & Caulk
A Simple Program
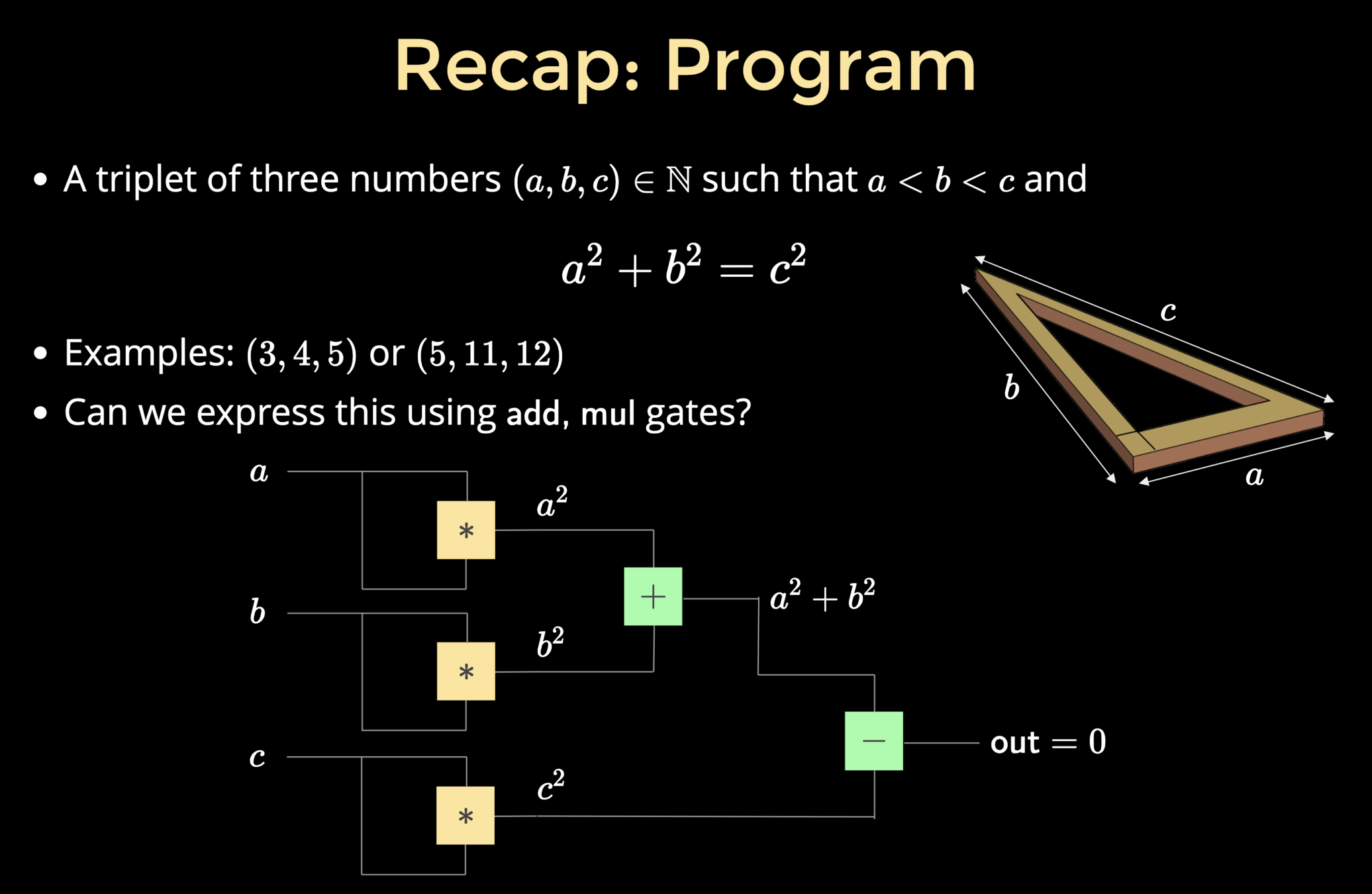
- A triplet of three numbers \((a, b, c) \in \mathbb{N}\) such that \(a < b < c\) and
a^2+b^2=c^2
- Examples: \((3,4,5)\) or \((5,11,12)\)
- Can we express this using \(\textsf{add, mul}\) gates?

b
c
a
a
\(\ast\)
b
\(\ast\)
c
\(\ast\)
\(+\)
\(-\)
\textsf{out} = 0
a^2
b^2
c^2
a^2+b^2
Constraints
x_1
\(\ast\)
x_2
\(\ast\)
x_3
\(\ast\)
\(+\)
x_4
x_5
x_6
- Each gate has three wires: \(w_l, w_r, w_o\)
\textcolor{gray}{0\cdot} x_1 + \textcolor{gray}{0\cdot}x_1 + \textcolor{gray}{1\cdot}(x_1x_1) \textcolor{gray}{-1\cdot}x_4 + \textcolor{gray}{0} = 0
\textcolor{gray}{1\cdot}x_4 + \textcolor{gray}{1\cdot}x_5 + \textcolor{gray}{0\cdot}(x_4x_5) \textcolor{gray}{-1\cdot}x_6 + 0 = 0
1
2
3
4
x_1
x_1
x_4
x_1^2 = x_4
x_2
x_2
x_5
x_2^2=x_5
x_3
x_3
x_6
x_3^2=x_6
x_4
x_5
x_6
x_4+x_5=x_6
\textcolor{gray}{0\cdot} x_2 + \textcolor{gray}{0\cdot}x_2 + \textcolor{gray}{1\cdot}(x_2x_2) \textcolor{gray}{-1\cdot}x_5 + \textcolor{gray}{0} = 0
\textcolor{gray}{0\cdot} x_3 + \textcolor{gray}{0\cdot}x_3 + \textcolor{gray}{1\cdot}(x_3x_3) \textcolor{gray}{-1\cdot}x_6 + \textcolor{gray}{0} = 0
- Gate constraint: \(\textcolor{gray}{q_l\cdot}w_l + \textcolor{gray}{q_r\cdot}w_r + \textcolor{gray}{q_m\cdot}w_lw_r + \textcolor{gray}{q_o\cdot}w_o + \textcolor{gray}{q_c} = 0\)
w_l
w_r
w_o
\text{Constraint}
i
Selectors
Witnesses
Constraints
x_1
\(\ast\)
x_2
\(\ast\)
x_3
\(\ast\)
\(+\)
x_4
x_5
x_6
- Each gate has three wires: \(w_l, w_r, w_o\)
1
2
3
4
x_1
x_1
x_4
x_1^2 = x_4
x_2
x_2
x_5
x_2^2=x_5
x_3
x_3
x_6
x_3^2=x_6
x_4
x_5
x_6
x_4+x_5=x_6
- Copy constraints:
w_l
w_r
w_o
\text{Constraint}
i
\begin{aligned}
(w_{o})_1 = (w_l)_4 \\[5pt]
(w_{o})_2 = (w_r)_4 \\[5pt]
(w_{o})_3 = (w_o)_4
\end{aligned}
1
2
3
4
- We can combine gate and copy constraints in a single huge equation!
- How do we prove the correctness of a set of equations?
\textcolor{gray}{0\cdot} x_1 + \textcolor{gray}{0\cdot}x_1 + \textcolor{gray}{1\cdot}(x_1x_1) \textcolor{gray}{-1\cdot}x_4 + \textcolor{gray}{0} = 0
\textcolor{gray}{1\cdot}x_4 + \textcolor{gray}{1\cdot}x_5 + \textcolor{gray}{0\cdot}(x_4x_5) \textcolor{gray}{-1\cdot}x_6 + \textcolor{gray}{0} = 0
\textcolor{gray}{0\cdot} x_2 + \textcolor{gray}{0\cdot}x_2 + \textcolor{gray}{1\cdot}(x_2x_2) \textcolor{gray}{-1\cdot}x_5 + \textcolor{gray}{0} = 0
\textcolor{gray}{0\cdot} x_3 + \textcolor{gray}{0\cdot}x_3 + \textcolor{gray}{1\cdot}(x_3x_3) \textcolor{gray}{-1\cdot}x_6 + \textcolor{gray}{0} = 0
\textcolor{gray}{q_l(X)}w_l(X) + \textcolor{gray}{q_r(X)}w_r(X) + \textcolor{gray}{q_m(X)}w_l(X)w_r(X) + \textcolor{gray}{q_o(X)}w_o(X) + \textcolor{gray}{q_c}(X) = 0
- Gate constraints done! What about copy constraints?
\begin{bmatrix}
\textcolor{orange}{a_1} \\
\textcolor{green}{a_2} \\
\textcolor{violet}{a_3}
\end{bmatrix}
\begin{bmatrix}
\textcolor{green}{b_1} \\
\textcolor{violet}{b_2} \\
\textcolor{orange}{b_3}
\end{bmatrix}
(\textcolor{orange}{a_1} + 1\beta + \gamma)\cdot(\textcolor{green}{a_2} + 2\beta + \gamma)\cdot(\textcolor{violet}{a_2} + 3\beta + \gamma)
\ =
(\textcolor{green}{b_1} + 2\beta + \gamma) \cdot
(\textcolor{violet}{b_2} + 3\beta + \gamma) \cdot
(\textcolor{orange}{b_3} + 1\beta + \gamma)
Polynomials


\pi
Proof
Back to Constraints
\textcolor{gray}{2.} a_1
\textcolor{gray}{+3.}b_1
\textcolor{gray}{+1.}c_1
\textcolor{gray}{-1.}d_1
\textcolor{gray}{+5} = 0
\textcolor{gray}{0.} a_3
\textcolor{gray}{+0.}b_3
\textcolor{gray}{+1.}a_3b_3
\textcolor{gray}{-1.}c_3
\textcolor{gray}{+0} = 0
(a_i,b_i) \ \textcolor{grey}{+_{\text{ecc}}} \ (c_i, d_i) = (a_{i+1},b_{i+1})
\textsf{ecc gate}:
\underbrace{\hspace{2cm}}
StandardPlonk
\underbrace{\hspace{1cm}}
TurboPlonk
\textsf{a}
\textsf{b}
\textsf{c}
\textsf{d}
i
1
a_1
b_1
c_1
d_1
2
a_2
b_2
c_2
d_2
3
a_3
b_3
c_3
d_3
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
i
a_{i}
b_{i}
c_{i}
d_{i}
i+1
a_{i+1}
b_{i+1}
c_{i+1}
d_{i+1}
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
n-1
a_{n-1}
b_{n-1}
c_{n-1}
d_{n-1}
n
a_{n}
b_{n}
c_{n}
d_{n}
\textsf{add gate}:
\textsf{mult gate}:
Width = \(4\)
Circuit size = \(n\)
c_1 = a_i,
d_2 = b_i,
a_{i+1} = c_{n-1},
b_{i+1} = d_{n-1},
\underbrace{\hspace{1cm}}
Copy constraints
Cell-wise permutation
Plookup
\textsf{a}
\textsf{b}
\textsf{c}
\textsf{d}
i
1
a_1
b_1
c_1
d_1
2
a_2
b_2
c_2
d_2
3
a_3
b_3
c_3
d_3
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
i
a_{i}
b_{i}
c_{i}
d_{i}
i+1
a_{i+1}
b_{i+1}
c_{i+1}
d_{i+1}
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
n-1
a_{n-1}
b_{n-1}
c_{n-1}
d_{n-1}
n
a_{n}
b_{n}
c_{n}
d_{n}
Width = \(4\)
Circuit size = \(n\)
\textsf{key}_1
\textsf{key}_2
\textsf{key}_3
\textsf{val}
t_1^{(1)}
t_1^{(2)}
t_1^{(3)}
v_1
t_2^{(1)}
t_2^{(2)}
t_2^{(3)}
v_2
t_3^{(1)}
t_3^{(2)}
t_3^{(3)}
v_3
t_l^{(1)}
t_l^{(2)}
t_l^{(3)}
v_l
Lookup Table \(T\)
Lookup table size = \(l\)
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
Lookup argument:
(a_i,b_i,c_i,d_i) \in T
\underbrace{\hspace{8.5cm}}
PLookup
Plookup
\textsf{a}
\textsf{b}
\textsf{c}
\textsf{d}
i
1
a_1
b_1
c_1
d_1
2
a_2
b_2
c_2
d_2
3
a_3
b_3
c_3
d_3
\vdots
\vdots
\vdots
\vdots
\vdots
i
a_{i}
b_{i}
c_{i}
d_{i}
i+1
a_{i+1}
b_{i+1}
c_{i+1}
d_{i+1}
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
n-1
a_{n-1}
b_{n-1}
c_{n-1}
d_{n-1}
n
a_{n}
b_{n}
c_{n}
d_{n}
Width = \(4\)
Circuit size = \(n\)
\textsf{key}_1
\textsf{key}_2
\textsf{key}_3
\textsf{val}
t_1^{(1)}
t_1^{(2)}
t_1^{(3)}
v_1
t_2^{(1)}
t_2^{(2)}
t_2^{(3)}
v_2
t_3^{(1)}
t_3^{(2)}
t_3^{(3)}
v_3
t_{l-2}^{(1)}
t_{l-2}^{(2)}
t_{l-2}^{(3)}
v_{l-2}
Lookup Table \(T\)
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
t_{l-1}^{(1)}
t_{l-1}^{(2)}
t_{l-1}^{(3)}
v_{l-1}
t_l^{(1)}
t_l^{(2)}
t_l^{(3)}
v_l
i-1
a_{i-1}
b_{i-1}
c_{i-1}
d_{i-1}
Lookup table size = \(l\)
Plookup
\textsf{a}
\textsf{b}
\textsf{c}
\textsf{d}
i
1
a_1
b_1
c_1
d_1
2
a_2
b_2
c_2
d_2
3
a_3
b_3
c_3
d_3
\vdots
\vdots
\vdots
\vdots
\vdots
i
a_{i}
b_{i}
c_{i}
d_{i}
i+1
a_{i+1}
b_{i+1}
c_{i+1}
d_{i+1}
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
n-1
a_{n-1}
b_{n-1}
c_{n-1}
d_{n-1}
n
a_{n}
b_{n}
c_{n}
d_{n}
Width = \(4\)
Circuit size = \(n\)
\textsf{key}_1
\textsf{key}_2
\textsf{key}_3
\textsf{val}
t_1^{(1)}
t_1^{(2)}
t_1^{(3)}
v_1
t_2^{(1)}
t_2^{(2)}
t_2^{(3)}
v_2
t_3^{(1)}
t_3^{(2)}
t_3^{(3)}
v_3
t_{l-2}^{(1)}
t_{l-2}^{(2)}
t_{l-2}^{(3)}
v_{l-2}
Lookup Table \(T\)
Lookup table size = \(l\)
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
\vdots
Multi-set check:
\{\eta_j\}_{j\in[m]} \in \{t_i\}_{i\in[l]}
t_{l-1}^{(1)}
t_{l-1}^{(2)}
t_{l-1}^{(3)}
v_{l-1}
t_l^{(1)}
t_l^{(2)}
t_l^{(3)}
v_l
i-1
a_{i-1}
b_{i-1}
c_{i-1}
d_{i-1}
\eta_1
\eta_2
\eta_3
\eta_m
\vdots
t_{l}
t_1
t_2
t_3
t_{l-2}
t_{l-1}
Can be written in a form similar to the permutation argument!
Wait, Why Plookup?
- Lets take a peek into the SHA-256 internals


XOR
AND
Right-rotate
Shift-right
- Tons of bitwise operations! Very fast on CPUs!


Caulk vs Plookup
- Plookup enables efficient bitwise or any operations in circuits
- But, what's the tradeoff? If the total lookup table size is \(N\)
\textsf{Prover} \approx \mathcal{O}(\text{max}(n\text{log}(n), N\text{log}(N)))
- Caulk does better: for \(m\) lookups
\textsf{Prover} \approx \mathcal{O}\big(n \text{log}(n) + m\text{log}(N) + m^2\big)
- Caulk pays in terms of pre-processing and storage
\textsf{pre-processing} \approx \mathcal{O}\big(N\text{log}(N)\big)
\textsf{storage} \approx \mathcal{O}\big(N\big)
Kate Primer
- The commit phase: for some secret scalar \(s \in \mathbb{F}_q\)
\textsf{commit}\left(\textcolor{lightgreen}{f}\right) \equiv f(s)= c_0 + c_1s + \dots + c_{n-1}s^{n-1}
- The open phase: given a challenge \(z\in \mathbb{F}_q,\) we compute:
\(\begin{aligned}\textsf{open}\left(f, z\right) \equiv w(s)= \frac{f(s)-f(z)}{s-z}\end{aligned}\)
opening polynomial
opening point
- The opening proof: \(\pi = \big\{\textcolor{lightgreen}{[w(s)]_1, f(z)}\big\}\)
- The verification:
\textsf{verify}\left(\pi, z\right) \equiv \textcolor{lightgreen}{w(s)}\cdot (s-z) \stackrel{?}{=} (\textcolor{lightgreen}{f(s)}-\textcolor{lightgreen}{f(z)})
e(\textcolor{lightgreen}{[w(s)]_1}, \ [s]_2-[z]_2) \stackrel{?}{=} (\textcolor{lightgreen}{[f(s)]_1}-\textcolor{lightgreen}{f(z)}\cdot [1]_1, \ [1]_2)
Caulk: Main Idea
a_{1}
a_{2}
a_{3}
\vdots
a_{m-1}
a_{m}
c_{1}
c_{2}
c_{3}
\vdots
c_{N-1}
c_{N}
\vdots
\vdots
c_{N-2}
c_{N-3}
\vec{a}
\vec{c}
\vec{a} \in \vec{c}
\implies a_{j} \in \vec{c} \qquad \forall j \in [m]
\omega^{0}
\omega^{1}
\omega^{2}
\vdots
\omega^{N-2}
\omega^{N-1}
\vdots
\vdots
\omega^{N-3}
\omega^{N-4}
\omega^{i_1}
\omega^{i_2}
\omega^{i_3}
\vdots
\omega^{i_{m-1}}
\omega^{i_m}
\mathbb{H}
\mathbb{H}_I
\nu^0
\nu^{1}
\nu^{2}
\vdots
\nu^{m-2}
\nu^{m-1}
\mathbb{V}_m
- Write \(\vec{c}\) and \(\vec{a}\) as a polynomials:
C(X) = \sum_{i=1}^{N} \textcolor{orange}{c_i} \cdot \textcolor{gray}{L_{\mathbb{H},i}(X)}
A(X) = \sum_{j=1}^{m} \textcolor{lightgreen}{a_j} \cdot \textcolor{gray}{L_{\mathbb{V}_m,j}(X)}
- Index set \(I = \{i_j\}_{j\in[m]} \subset [N]\) and subset of roots \(\mathbb{H}_I\)
C_I(X) = \sum_{j=1}^{m} \textcolor{orange}{c_{i_j}} \cdot \textcolor{gray}{L_{\mathbb{H}_I,j}(X)}
- High-level idea: Compute a KZG-like formulation
\begin{aligned}
Q_1(X) = \frac{C(X) - C_I(X)}{z_I(X)}
\end{aligned}
Caulk: Precomputation
a_{1}
a_{2}
a_{3}
\vdots
a_{m-1}
a_{m}
c_{1}
c_{2}
c_{3}
\vdots
c_{N-1}
c_{N}
\vdots
\vdots
c_{N-2}
c_{N-3}
\vec{a}
\vec{c}
\omega^{0}
\omega^{1}
\omega^{2}
\vdots
\omega^{N-2}
\omega^{N-1}
\vdots
\vdots
\omega^{N-3}
\omega^{N-4}
\omega^{i_1}
\omega^{i_2}
\omega^{i_3}
\vdots
\omega^{i_{m-1}}
\omega^{i_m}
\mathbb{H}
\mathbb{H}_I
\nu^0
\nu^{1}
\nu^{2}
\vdots
\nu^{m-2}
\nu^{m-1}
\mathbb{V}_m
- Step 1: Compute \([Q_1]_1\), where \(Q_1(X)\) is quotient poly
\begin{aligned}
Q_1(X) = \frac{C(X) - C_I(X)}{z_I(X)}
\end{aligned}
- Problem: Degree of \(C\) and \(Q_1\) is \(N\)!
- Using precomputed KZG proofs, we can:
Q_{1}
Q_{2}
Q_{3}
\vdots
Q_{N-1}
Q_{N}
\vdots
\vdots
Q_{N-2}
Q_{N-3}
\pi_{\textsf{\tiny KZG}}
\begin{aligned}
[Q_1]_2 = \sum_{j=1}^{m}\frac{\textcolor{violet}{Q_i}}{\prod_{k\neq j}(\omega^{i_j} - \omega^{i_k})}
\end{aligned}
- Precomputing \(N\) KZG proofs takes:
- Computation: \(\mathcal{O}(N \text{log}N)\)
- Storage: \(\mathcal{O}(N)\)
Caulk: Main Idea
a_{1}
a_{2}
a_{3}
\vdots
a_{m-1}
a_{m}
c_{1}
c_{2}
c_{3}
\vdots
c_{N-1}
c_{N}
\vdots
\vdots
c_{N-2}
c_{N-3}
\vec{a}
\vec{c}
\omega^{0}
\omega^{1}
\omega^{2}
\vdots
\omega^{N-2}
\omega^{N-1}
\vdots
\vdots
\omega^{N-3}
\omega^{N-4}
\omega^{i_1}
\omega^{i_2}
\omega^{i_3}
\vdots
\omega^{i_{m-1}}
\omega^{i_m}
\mathbb{H}
\mathbb{H}_I
\nu^0
\nu^{1}
\nu^{2}
\vdots
\nu^{m-2}
\nu^{m-1}
\mathbb{V}_m
- Step 2: Prove that \(z_I(X)\) is indeed of correct form
- For this, we define
\begin{aligned}
u(X) = \sum_{j\in[m]} \omega^{i_j} \cdot \textcolor{gray}{L_{\mathbb{V}_m, j}(X)}
\end{aligned}
- Step 2.1: Compute \(\pi_{\text{unity}}\) which proves that \(u(X)\) has \(N\)-th roots of unity as evaluations on \(\textcolor{gray}{\mathbb{V}_m}\)
- This isn't enough: we need to prove that \(z_I(X)\) vanishes on \(\textcolor{gray}{\mathbb{H}_I}\)
- Idea: Evaluations of \(u(X)\) are roots of \(z_I(X)\)
- Step 2.2: Compute quotient polynomial \(Q_2(X)\) s.t.
\begin{aligned}
Q_2(X) = \frac{z_I(u(X))}{z_{\mathbb{V}_m}(X)}
\end{aligned}
Caulk: Main Idea
a_{1}
a_{2}
a_{3}
\vdots
a_{m-1}
a_{m}
c_{1}
c_{2}
c_{3}
\vdots
c_{N-1}
c_{N}
\vdots
\vdots
c_{N-2}
c_{N-3}
\vec{a}
\vec{c}
\omega^{0}
\omega^{1}
\omega^{2}
\vdots
\omega^{N-2}
\omega^{N-1}
\vdots
\vdots
\omega^{N-3}
\omega^{N-4}
\omega^{i_1}
\omega^{i_2}
\omega^{i_3}
\vdots
\omega^{i_{m-1}}
\omega^{i_m}
\mathbb{H}
\mathbb{H}_I
\nu^0
\nu^{1}
\nu^{2}
\vdots
\nu^{m-2}
\nu^{m-1}
\mathbb{V}_m
-
After Step 1 and 2, the prover sends:
- Commitment to \(\vec{a}\): \([A]_1\)
- Commitment to \(C_I(X)\): \([C_I]_1\)
- Commitment to vanishing polynomial: \([z_I]_1\)
- Commitment to roots-of-unity poly: \([u]_1\)
- Commitment to first quotient poly: \([Q_1]_2\)
- Unity proof: \(\pi_{\text{unity}}\)
- Why do we commit \(Q_1(X)\) in the second group?
\begin{aligned}
Q_1(X) = \frac{C(X) - C_I(X)}{z_I(X)}
\end{aligned}
\begin{aligned}
\implies Q_1(X) \cdot z_I(X) = (C(X) - C_I(X))
\end{aligned}
Caulk: Main Idea
a_{1}
a_{2}
a_{3}
\vdots
a_{m-1}
a_{m}
c_{1}
c_{2}
c_{3}
\vdots
c_{N-1}
c_{N}
\vdots
\vdots
c_{N-2}
c_{N-3}
\vec{a}
\vec{c}
\omega^{0}
\omega^{1}
\omega^{2}
\vdots
\omega^{N-2}
\omega^{N-1}
\vdots
\vdots
\omega^{N-3}
\omega^{N-4}
\omega^{i_1}
\omega^{i_2}
\omega^{i_3}
\vdots
\omega^{i_{m-1}}
\omega^{i_m}
\mathbb{H}
\mathbb{H}_I
\nu^0
\nu^{1}
\nu^{2}
\vdots
\nu^{m-2}
\nu^{m-1}
\mathbb{V}_m
- What remains to show is: linking of \(C_I(X)\) with \([A]_1\)
\begin{aligned}
\implies Q_3(X) = \frac{C_I(u(X)) - A(X)}{z_{\mathbb{V}_m}(X)}
\end{aligned}
A(X) = \sum_{j=1}^{m} \textcolor{lightgreen}{a_j} \cdot \textcolor{gray}{L_{\mathbb{V}_m,j}(X)}
C_I(X) = \sum_{j=1}^{m} \textcolor{orange}{c_{i_j}} \cdot \textcolor{gray}{L_{\mathbb{H}_I,j}(X)}
- Notice that:
C_I(\omega^{i_j}) = \textcolor{orange}{c_{i_j}} = \textcolor{lightgreen}{a_j}
- Compute \([Q_3]_1\) and we're done!
- Last step: open all of these polys on a challenge point
Caulk vs Plookup
By Suyash Bagad
Caulk vs Plookup
- 213



