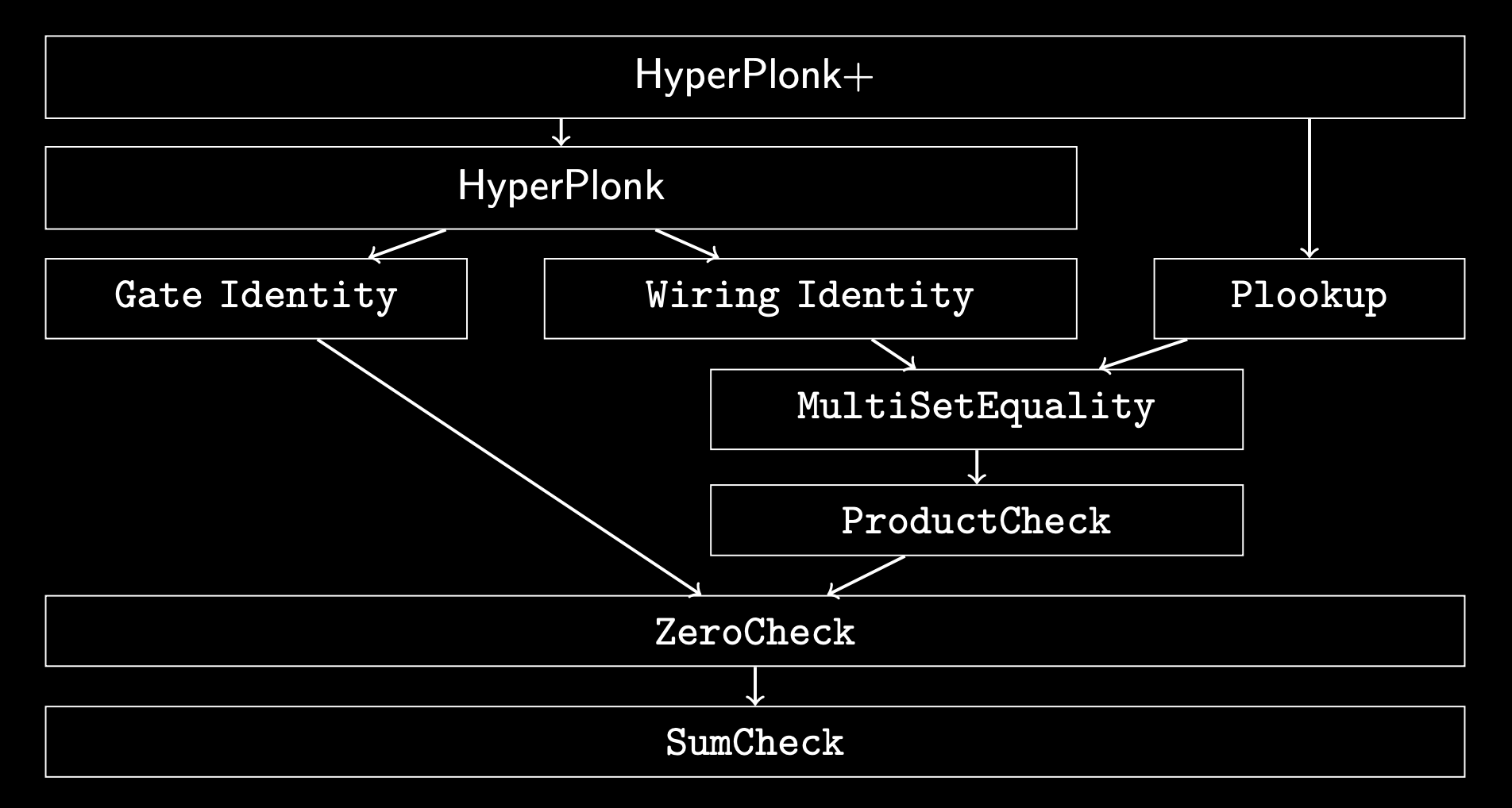
HyperPlonk
Part \(2\)
Polynomial Basis
X
f(X)
a(X)
\vec{a}
w_1
w_2
w_3
w_4
x
\omega_1
\omega_2
\omega_3
\omega_4
\vec{x}
(0,0)
(0,1)
(1,0)
(1,1)
w_1
w_2
w_3
w_4
X
f(X,Y)
Y
(0,0)
(1,0)
(0,1)
(1,1)
\omega^0
\omega^1
\omega^2
\omega^3
\underbrace{\hspace{5cm}}_{H}
w_1
w_2
w_3
w_4
HyperPlonk Recap
G
L_i
R_i
O_i
- Simple gate constraint: \(\forall i \in [2^\mu]\)
\begin{aligned}
& \textcolor{grey}{S_{\textsf{add}}(\vec{x})}
\Big( \textcolor{pink}{M(0,0,\vec{x})} + \textcolor{lightgreen}{M(0,1,\vec{x})} \Big)
+
\textcolor{grey}{S_{\textsf{mul}}(\vec{x})}
\Big(\textcolor{pink}{M(0,0,\vec{x})} \cdot \textcolor{lightgreen}{M(0,1,\vec{x})})
+ \\
& \textcolor{grey}{S_{\textsf{gate}}(\vec{x})}
G\Big[ \textcolor{pink}{M(0,0,\vec{x})}, \textcolor{lightgreen}{M(0,1,\vec{x})} \Big]
- \textcolor{skyblue}{M(1,0,\vec{x})} = 0
\end{aligned}
L_0
L_1
L_3
L_2
L_4
L_6
L_5
L_7
R_0
R_1
R_3
R_2
R_4
R_6
R_5
R_7
O_0
O_1
O_3
O_2
O_4
O_6
O_5
O_7
M(0,0,\vec{x}) \equiv L(\vec{x})
M(0,1,\vec{x}) \equiv R(\vec{x})
M(1,0,\vec{x}) \equiv O(\vec{x})
\begin{aligned}
& \textcolor{grey}{S_{\textsf{add}, i}}
\big( \textcolor{pink}{L_i} + \textcolor{lightgreen}{R_i} \big)
+
\textcolor{grey}{S_{\textsf{mul}, i}}
\big(\textcolor{pink}{L_i} \cdot \textcolor{lightgreen}{R_i}\big)
+
\textcolor{grey}{S_{\textsf{gate}, i}}
G\big( \textcolor{pink}{L_i}, \textcolor{lightgreen}{R_i} \big)
- \textcolor{skyblue}{O_i} = 0
\end{aligned}
- Gate constraint as a multi-variate polynomial identity: \(\forall \vec{x} \in B_\mu\)
\implies \Big\{f_{\textsf{gate}}(\vec{x}) = 0\Big\}_{\vec{x}\in B_{\mu+2}}
- Linearly combine \(\{f_{\textsf{gate}}(\vec{x})\}_{\vec{x} \in B_{\mu+2}}\) with \(\mu\) challenges
- ZeroCheck: Run a sum-check on \(\hat{f}_{\textsf{gate}}(\vec{X})\) with sum 0.
- For copy constraints, we had
HyperPlonk Recap
Sumcheck
ZeroCheck
f'(\vec{x}) := f(\vec{x}) + \textcolor{grey}{\beta}s_{\textsf{id}}(\vec{x}) + \textcolor{grey}{\gamma}
g'(\vec{x}) := g(\vec{x}) + \textcolor{grey}{\beta}s_{\sigma}(\vec{x}) + \textcolor{grey}{\gamma}
- ProductCheck: Run a product-check on \(\frac{f'}{g'}(\vec{X})\) with product 1.
\implies
\begin{aligned}
\prod_{\vec{x} \in B_\mu} \frac{f'(\vec{x})}{g'(\vec{x})}=1
\end{aligned}
ProdCheck
- We wanted to show that:
HyperPlonk In a Nutshell
\(\texttt{Gate Constraint}\)
\(\texttt{Copy Constraint}\)
Sumcheck
- Given a polynomial \(g: \mathbb{F}^\mu \rightarrow \mathbb{F}\) and \(X = \{x_i\}_{i \in [\mu]}\) compute the sum
\begin{aligned}
H = \sum_{X \in B_\mu} g(x_1, x_2, \dots, x_\mu)
\end{aligned}
- Intuition: evaluation on a boolean hypercube
\(g(x,y) = \frac{-4x}{(x^2+y^2+1)}\)
- Naively, a verifier would require \(2^\mu\) evaluations of \(g(.)\)
- Sumcheck protocol requires \(\mathcal{O}(\mu + \lambda)\) verifier work
- Here \(\lambda\) is the cost to evaluate \(g(.)\) at some \(r \in \mathbb{F}^{m}\)
- Prover's work is \(\mathcal{O}(2^\mu)\), i.e. linear in no of constraints
\begin{aligned}
H = g(0,0) + g(0,1) + g(1,0) + g(1,1)
\end{aligned}
= 0 + 0 - 2 - \frac{4}{3} = -\frac{10}{3}
Sumcheck
- Honest prover starts by computing \(v = \sum_{X \in \{0,1\}^\mu}g(x_1, x_2, \dots, x_\mu)\)
\(g_1(\textcolor{orange}{X_1}) := \sum_{x_2\dots}g(\textcolor{orange}{X_1},x_2, \dots, x_m)\)
\(g_2(\textcolor{orange}{X_2}) := \sum_{x_3\dots}g(\textcolor{green}{r_1}, \textcolor{orange}{X_2}, x_3, \dots, x_m)\)
\(v \stackrel{?}{=} g_1(0) + g_1(1)\)
\(g_1(\textcolor{green}{r_1}) \stackrel{?}{=} g_2(0) + g_2(1)\)
\(g_3(\textcolor{orange}{X_3}) := \sum_{x_4\dots}g(\textcolor{green}{r_1}, \textcolor{green}{r_2}, \textcolor{orange}{X_3}, x_4, \dots, x_m)\)
\(g_\mu(\textcolor{orange}{X_\mu}) := g(\textcolor{green}{r_1}, \textcolor{green}{r_2}, \dots, \textcolor{green}{r_{\mu-1}}, \textcolor{orange}{X_\mu})\)
\(g_2(\textcolor{green}{r_2}) \stackrel{?}{=} g_3(0) + g_3(1)\)
\(g_{\mu-1}(\textcolor{green}{r_{\mu-1}}) \stackrel{?}{=} g_\mu(0) + g_\mu(1)\)
\(g_{\mu}(\textcolor{green}{r_{\mu}}) \stackrel{?}{=} g(\textcolor{green}{r_1}, \textcolor{green}{r_2}, \dots, \textcolor{green}{r_\mu})\)
Prover \(\mathcal{P}\)
Verifier \(\mathcal{V}\)
\(g_1\)
\(r_1\)
\(g_2\)
\(g_3\)
\(g_\mu\)
\(r_{\mu-1}\)
\(r_2\)
\(\vdots\)
\(\vdots\)
\(\vdots\)
Sumcheck Costs
-
Prover costs:
- In round \(i\in[\mu]\), evaluate \(g_i(\vec{x})\):
- \(g_i(\textcolor{orange}{X}) := \sum_{\vec{x}\in B_{\mu-i}}g(\textcolor{green}{r_1, \dots, r_{i-1}}, \textcolor{orange}{X}, \vec{x})\)
- \(\text{deg}_X(g_i) := \text{deg}_{x_i}(g) \le d\)
- No of evaluations: \(|B_{\mu-i}| = 2^{\mu-i}\)
- Total evaluations: \(\sum_{i}\text{deg}_{x_i}(g) \cdot 2^{\mu-i} = \textcolor{skyblue}{d \cdot 2^\mu}\)
-
Verifier costs:
- In round \(i\), evaluate \(g_i(0), g_i(1), g_{i-1}(r_{i-1}) \implies O(\mu)\)
- Cost of evaluating \(g(\vec{x})\) on \(\vec{x} = (r_1, \dots, r_\mu)\)
-
Proof size:
- \(\sum_{i} (\text{deg}_{x_i}(g) + 1) = \textcolor{skyblue}{(d + 1)\mu}\)
Non-Interactive Sumcheck
1
g_1(\textcolor{orange}{X_1}) := \sum_{x_2\dots}g(\textcolor{orange}{X_1},x_2, \dots, x_\mu)
\textcolor{skyblue}{[[g_1]],} \
\textcolor{lightgreen}{g_1(0), g_1(1), v}
2
g_2(\textcolor{orange}{X_2}) := \sum_{x_3\dots}g(\textcolor{green}{r_1}, \textcolor{orange}{X_2}, x_3, \dots, x_\mu)
\textcolor{skyblue}{[[g_2]],} \
\textcolor{lightgreen}{g_2(0), g_2(1), g_1(r_1)}
3
g_3(\textcolor{orange}{X_3}) := \sum_{x_4\dots}g(\textcolor{green}{r_1}, \textcolor{green}{r_2}, \textcolor{orange}{X_3}, x_4, \dots, x_\mu)
\textcolor{skyblue}{[[g_3]],} \
\textcolor{lightgreen}{g_3(0), g_3(1), g_2(r_2)}
\mu
g_\mu(\textcolor{orange}{X_\mu}) := g(\textcolor{green}{r_1}, \textcolor{green}{r_2}, \dots, \textcolor{green}{r_{\mu-1}}, \textcolor{orange}{X_m})
\textcolor{skyblue}{[[g_\mu]],} \
\textcolor{lightgreen}{g_\mu(0), g_\mu(1), g_{\mu-1}(r_{\mu-1})}
\vdots
\vdots
\vdots
\textcolor{grey}{\textsf{open}}
\left(
\left\{
g_i(X_i)
\right\}
\text{ at }
\left\{
0, 1, r_i
\right\}
\right)
\quad \forall i \in [\mu]
\textcolor{skyblue}{\left\{[[q_1]], [[q_2]], \dots, [[q_{\mu+2}]]\right\},}
\textcolor{lightgreen}{ g_\mu(r_\mu)}
- Proof size: \(\#\mathbb{G} = 2\mu+2\) and \(\# \mathbb{F} = 3\mu\)
-
Prover computation with KZG:
- \(2\mu+2\) MSMs of size \((d+1),\)
- Evaluations: \(d\times 2^{\mu}\)
- Verifier: 1 MSM of \(O(\mu)\) and 1 pairing
-
Prover computation with Shplonk:
- \(\mu+2\) MSMs of size \((d+1),\)
- Evaluations: \(d\times 2^{\mu}\)
Non-Interactive Sumcheck 🚀
\textcolor{grey}{\textsf{open}}
\left(
\left\{
g'_i(X_i)
\right\}
\text{ at }
\{r_i\}
\right)
\quad \forall i \in [\mu]
- Proof size: \(\mathbb{G} \rightarrow 2\mu+1, \mathbb{F} \rightarrow 2\mu\)
- Prover computation improvement: \(\mu+2\) MSMs of size \(d\)
\textcolor{olive}{g_i(1)} := v - \textcolor{lightgreen}{g_i(0)}
v \leftarrow \textcolor{olive}{g_i(r_i)} := \textcolor{lightgreen}{g'_i(r_i)}\cdot r_i(1-r_i) + \textcolor{lightgreen}{g_i(0)}(1-r_i)
+\textcolor{olive}{g_i(1)}(r_i)
- The verifier can compute the other two evaluations using \(\textcolor{lightgreen}{g_i(0), g'(r_i)}\)
- This would require prover to open \(g'_i(X)\) only at \(r_i\):
i
g_i(\textcolor{orange}{X}) := \sum_{x_i\dots}g(\textcolor{green}{r_1, \dots, r_{i-1},}
\textcolor{orange}{X}, x_{i+1}, \dots, x_{\mu})
\begin{aligned}
g'_i(\textcolor{orange}{X}) :=
\frac{
g_i(\textcolor{orange}{X}) - (1-\textcolor{orange}{X})g_i(0) + (\textcolor{orange}{X})g_i(1)
}
{
\textcolor{orange}{X}(1-\textcolor{orange}{X})
}
\end{aligned}
\textcolor{skyblue}{[[g'_i]],} \
\textcolor{lightgreen}{g_i(0), g_i'(r_i)}
HyperPlonk Unrolled
w =
\begin{pmatrix}
\textcolor{pink}{L_1} & \textcolor{lightgreen}{R_1} & \textcolor{lightblue}{O_1} \\
\textcolor{pink}{L_2} & \textcolor{lightgreen}{R_2} & \textcolor{lightblue}{O_2} \\
\textcolor{pink}{L_3} & \textcolor{lightgreen}{R_3} & \textcolor{lightblue}{O_3} \\
\vdots & \vdots & \vdots \\
\textcolor{pink}{L_{2^\mu}} & \textcolor{lightgreen}{R_{2^\mu}} & \textcolor{lightblue}{O_{2^\mu}} \\
\end{pmatrix}
\textsf{ML commit}
[[w]]
\textsf{ML eval}
\hat{f}_{\textsf{gate}} \in \mathbb{F}^{\le d}_{\mu+2}
\hat{f}_{\textsf{copy}} \in \mathbb{F}^{\le d}_{\mu+2+1}
\textsf{ML eval}
\textsf{batch sumcheck}
\hat{f}_{\textsf{combined}} \in \mathbb{F}^{\le d}_{\mu+3}
\begin{pmatrix}
\textcolor{skyblue}{[[g_1]]} & \textcolor{lightgreen}{g_1(0)} & \textcolor{lightgreen}{g'_1(r_1)} \\
\textcolor{skyblue}{[[g_2]]} & \textcolor{lightgreen}{g_2(0)} & \textcolor{lightgreen}{g'_2(r_1)} \\
\textcolor{skyblue}{[[g_3]]} & \textcolor{lightgreen}{g_3(0)} & \textcolor{lightgreen}{g'_3(r_1)} \\
\vdots & \vdots & \vdots \\
\textcolor{skyblue}{[[g_{\mu+3}]]} & \textcolor{lightgreen}{g_{\mu+3}(0)} & \textcolor{lightgreen}{g'_{\mu+3}(r_{\mu+3})} \\
\end{pmatrix}
\textsf{shplonk}
\big\{f_{\textsf{compressed}}(z) = y\big\}
\textsf{batch eval}
\big\{f_{\textsf{compressed}}(z) = y\big\}\\
\big\{w(z_1) = y_1\big\} \\
\big\{w(z_2) = y_2\big\} \\
\dots \\
\big\{f(z_k) = y_k\big\}
HyperPlonk Part 2
By Suyash Bagad
