Performance Trade-offs in Design of MimbleWimble Proofs of Reserves
Suyash Bagad, Saravanan Vijayakumaran
Department of Electrical Engineering, IIT Bombay
IEEE Security & Privacy on the Blockchain, 2020
September 7, 2020
Outline
What is a proof of reserves? Why is it necessary?
Revelio - current state-of-the-art for MimbleWimble
RevelioBP - a Bulletproofs based proof of reserves for MimbleWimble
Performance comparison of RevelioBP and Revelio
Future scope
Proof of Reserves
Proof of ownership of a certain amount of assets
For crypto exchanges, challenge is proving this without revealing any sensitive information
Exchanges
UTXO Set
\(a_1\)
\(a_2\)
\(a_3\)
\(a_4\)
\(\texttt{We own some addresses}\)
\(\texttt{which contain a total of}\)
\(\texttt{an amount hidden in a}\)
\(\texttt{Pedersen commitment } C_{\text{res}}.\)
Reserves: \(C_{\text{res}} = g^{r_1} \cdot h^{\sum_{i} a_i},\)
Proof of solvency: \(C_{\text{res}} \cdot C_{\text{liab}}^{-1} \) commits to an integer in range \([0, M], M > 0\)
Liabilities: \(C_{\text{liab}}=g^{r_2} \cdot h^{\sum_{i} l_i}\)
Revelio
\mathcal{C}_{\text{own}}
C = g^{k} \cdot h^{a}
C \in \mathcal{C}_{\text{own}} \Longleftrightarrow k \text{ is known}
Each output in MimbleWimble is a Pedersen Commitment
Pedersen Commitments are homomorphic, perfectly hiding and computationally binding
For an amount \(a \in \{0,1,\dots,2^{64}-1\}\) and blinding factor \(k \in \mathbb{Z}_q\)
Let \(\mathbb{G}\) be a prime ordered group (\(|\mathbb{G}|=q\)) with generators \(g,h \in \mathbb{G}\) such that DL relation between them is unknown
Revelio
\mathcal{C}_{\text{anon}}
1
2
3
4
5
6
7
8
9
10
12
11
13
Proves that each \( C_i \in \mathcal{C}_{\text{anon}},\) is either owned OR not owned by exchange
PoK\big\{\underbrace{(\alpha,\beta,\gamma)}_{\text{secret}} \ | \ \underbrace{(C = g^{\alpha} \cdot h^{\beta} \ \wedge \ I = g_1^{\alpha} \cdot h^{\beta}) \vee (I = g_1^{\gamma}) }_{\text{statement}} \big\}
\Pi_{\text{Rev}} = \{(I_1, I_2, \dots, I_n), C_{\text{res}}, (\sigma_1, \dots, \sigma_n)\}
\(\sigma_i\) are NIZK proofs of representation of discrete log
Proof size linear in anonymity set size: \((n+1) \in \mathbb{G}, \ 5n \in \mathbb{Z}_q\)
Free choice of \(\mathcal{C}_{\text{anon}};\) Can we have \(\mathcal{C}_{\text{anon}}=\text{UTXO}?\)
RevelioBP!
RevelioBP!
1
2
3
4
5
6
7
8
9
10
12
11
13
0
1
0
0
0
0
0
0
0
0
0
0
0
(
)
\textbf{e}_1 =
0
0
0
0
0
1
0
0
0
0
0
0
0
(
)
\textbf{e}_2 =
0
0
0
0
0
0
0
0
1
0
0
0
0
(
)
\textbf{e}_3 =
0
0
0
0
0
0
0
0
0
1
0
0
0
(
)
\textbf{e}_4 =
0
0
0
0
0
0
0
0
0
0
0
0
1
(
)
\textbf{e}_5 =
k_1
k_2
k_3
k_4
k_5
(
)
\textbf{k} =
\Pi_{\text{RevBP}} = \left\{\textbf{I}=(I_1,\dots,I_{s}), C_{\text{res}}, \Pi_{\text{IP}}\right\}
PoK\left\{ \ (\textbf{k} \in \mathbb{Z}_q^s, \
\textbf{E} \in \mathbb{Z}_2^{s \times n}) \ | \
\textbf{C}^{\textbf{e}_j} = g^{k_j}h^{a_j}
\ \wedge \
\ I_j = g_t^{k_j}h^{a_j}
\ \forall j \in [s]
\ \right\}
More on RevelioBP
We then use the inner product argument of the form
PoK \left\{
(\textbf{a}, \textbf{b}) \in \mathbb{Z}_q^N \ | \
P = u^{c}\textbf{g}^{\textbf{a}} \textbf{h}^{\textbf{b}} \wedge c = \langle \textbf{a}, \textbf{b} \rangle \
\right\}
s + 2 \text{log}_2(sn+n+s+3) \text{ in } \mathbb{G}, \
5 \text{ in } \mathbb{Z}_q
| RevelioBP proof size | Revelio proof size |
(n+1) \text{ in } \mathbb{G}, \ 5n \text{ in } \mathbb{Z}_q
To build \(\Pi_{\text{IP}},\) we combine the constraints using a scalar \(u \leftarrow \mathbb{Z}_q\)
\prod_{j \in [s]} \left(g^{-k_j} \cdot g_t^{k_j} \cdot \textbf{C}^{\textbf{e}_{i_j}} \cdot I_j^{-1}\right)^{u^{j-1}} = 1,
\implies g^{- \langle \textbf{u}^s, \textbf{k} \rangle} \cdot
g_t^{\langle \textbf{u}^s, \textbf{k} \rangle} \cdot
\textbf{C}^{ \textbf{u}^s \textbf{E}} \cdot
\textbf{I}^{- \textbf{u}^s} = 1,
PoK\left\{ \ (\textbf{k} \in \mathbb{Z}_q^s, \
\textbf{E} \in \mathbb{Z}_2^{s \times n}) \ | \
\textbf{C}^{\textbf{e}_j} = g^{k_j}h^{a_j}
\ \wedge \
\ I_j = g_t^{k_j}h^{a_j}
\ \forall j \in [s]
\ \right\}
Proof Sizes
We implemented RevelioBP in Rust over \( \mathbb{G} = \texttt{secp256k1}\) elliptic curve
n \ \longrightarrow
s \ \longrightarrow
s=20
n=1000
\text{Proof size in KB} \longrightarrow
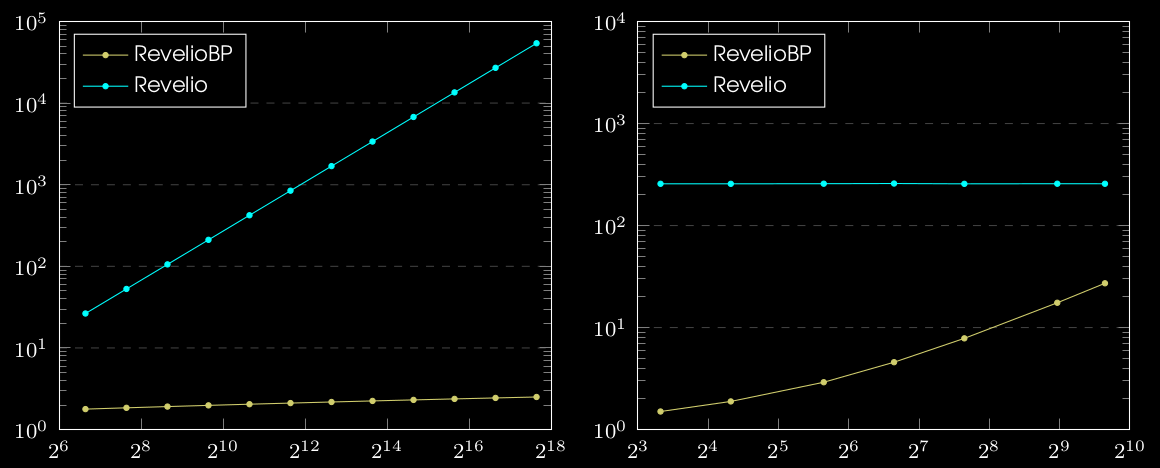
Note: All plots are in log-log scale.
RevelioBP proofs are \(\ge 10\text{X}\) shorter that that of Revelio
Running Times
RevelioBP proof generation is \(2\text{X}\) slower that of Revelio
n \ \longrightarrow
s \ \longrightarrow
s=20
n=1000
\text{Running time in mins} \longrightarrow
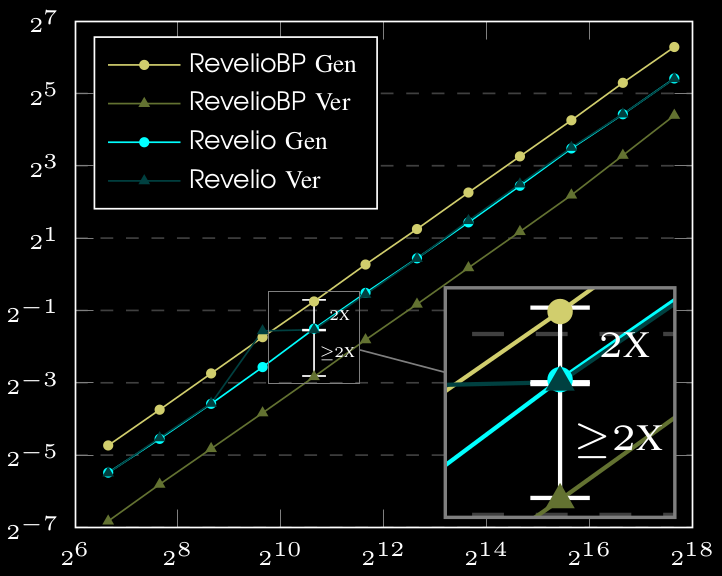
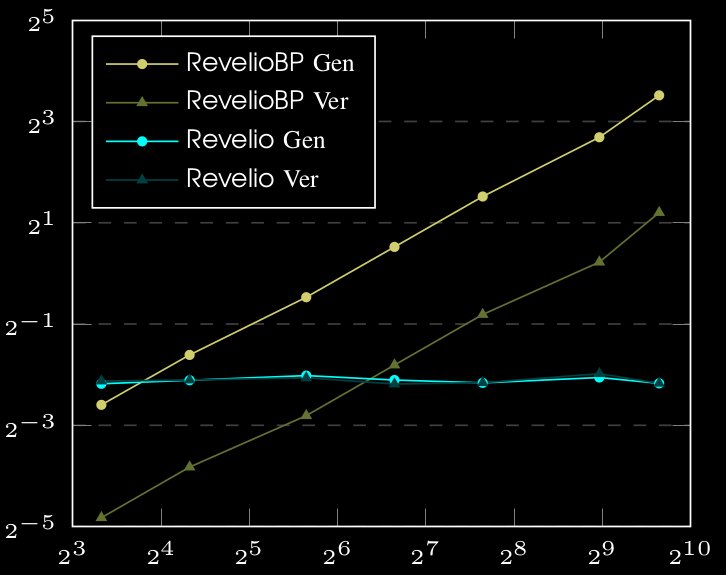
Note: All plots are in log-log scale.
RevelioBP ver. is \(4\text{X}\) faster than its gen. due to multi-exponentiation
Performance Trade-offs
| RevelioBP | Revelio | |
|---|---|---|
| Proof size | ||
| Scalability | ||
| Blockchain state | ||
| Output privacy | ||
| Inflation resistance | ||
| Own set size | ||
| Running times | ||
| Parallelizable |
\mathcal{O}(n)
\mathcal{O}(s+\text{log}_2(sn))
\mathcal{O}(sn)
\mathcal{O}(n)
For UTXO set size \(n=1.6\times 10^5\) and \(s=50\)
3.5\text{KB}
32\text{MB}
(140,35)\\[-3pt]
\text{min}
(34,34)\\[-3pt]
\text{min}
\(100\)
(300,72)\\[-3pt]
\text{min}
(34,34)\\[-3pt]
\text{min}
Future Scope
Proof of reserves using other proof systems: zk-SNARKs like PLONK, Sonic for \(\mathcal{O}(1)\)-time verification - will require additional assumptions
Extend it to other cryptocurrencies - work in progress for Monero
References
- [This work] S. Bagad and S. Vijayakumaran, "Performance Trade-offs in Design of MimbleWimble Proofs of Reserves," In 2020 Cryptology ePrint Archive, Report 2020/938.
- A. Dutta and S. Vijayakumaran, "Revelio: A MimbleWimble Proof of Reserves Protocol," 2019 Crypto Valley Conference on Blockchain Technology (CVCBT), Rotkreuz, Switzerland, 2019, pp. 7-11, doi: 10.1109/CVCBT.2019.000-5.
-
B. Bünz et al., "Bulletproofs: Short Proofs for Confidential Transactions and More," 2018 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, 2018, pp. 315-334, doi: 10.1109/SP.2018.00020.
-
Russell W. F. Lai et al., "Omniring: Scaling Private Payments Without Trusted Setup". In Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security (CCS '19). ACM, New York, NY, USA, 31–48. DOI: 10.1145/3319535.3345655
-
G. Dagher et al. "Provisions: Privacy-preserving Proofs of Solvency for Bitcoin Exchanges". In Proceedings of the 2015 ACM SIGSAC Conference on Computer and Communications Security. ACM, New York, NY, USA, 720–731. DOI: 10.1145/2810103.2813674
RevelioBP at IEEE S&B 2020 v2
By Suyash Bagad
RevelioBP at IEEE S&B 2020 v2
Interactive presentation of the paper "Performance Trade-offs in Design of MimbleWimble Proofs of Reserves" at IEEE S&B 2020.
