Sumcheck-IPA
Inner Product Argument
\begin{matrix}
\textcolor{orange}{\vec{a}} =
\big[ \ \textcolor{orange}{a_1} & \textcolor{orange}{a_2} & \textcolor{orange}{a_3} & \textcolor{orange}{a_4} \ \big] \\[6pt]
\textcolor{grey}{\vec{b}} =
\big[ \ \textcolor{grey}{b_1} & \textcolor{grey}{b_2} & \textcolor{grey}{b_3} & \textcolor{grey}{b_4} \ \big] \\[15pt]
\textcolor{grey}{\vec{G}} = \big[ \ \textcolor{grey}{G_1} & \textcolor{grey}{G_2} & \textcolor{grey}{G_3} & \textcolor{grey}{G_4} \ \big]
\end{matrix}
\textcolor{orange}{z} :=
\langle \textcolor{orange}{\vec{a}}, \textcolor{grey}{\vec{b}} \rangle =
\sum_{i=1}^{4}\textcolor{orange}{a_i} \cdot \textcolor{grey}{b_i}
secret
public
\textcolor{lightgreen}{A} :=
\langle \textcolor{orange}{\vec{a}}, \textcolor{grey}{\vec{G}} \rangle + \textcolor{orange}{z} \cdot \textcolor{grey}{U}
public
inner-product
commitment
\begin{matrix}
\textcolor{orange}{\vec{a}_{\textsf{next}}} =
\textcolor{grey}{\frac{1}{x}}\big[ \ \textcolor{orange}{a_1} & \textcolor{orange}{a_2} \ \big] & + &
\textcolor{grey}{x}\big[ \ \textcolor{orange}{a_3} & \textcolor{orange}{a_4} \ \big] \\[6pt]
\textcolor{grey}{\vec{b}_{\textsf{next}}} =
\textcolor{grey}{x}\big[ \ \textcolor{grey}{b_1} & \textcolor{grey}{b_2} \ \big] & + &
\textcolor{grey}{\frac{1}{x}}\big[ \ \textcolor{grey}{b_3} & \textcolor{grey}{b_4} \ \big] \\[8pt]
\textcolor{grey}{\vec{G}_{\textsf{next}}} =
\textcolor{grey}{x}\big[ \ \textcolor{grey}{G_1} & \textcolor{grey}{G_2} \ \big] & + &
\textcolor{grey}{\frac{1}{x}}\big[ \ \textcolor{grey}{G_3} & \textcolor{grey}{G_4} \ \big]
\end{matrix}
\begin{matrix}
\big[ \
\textcolor{grey}{\frac{1}{x}}\textcolor{orange}{a_1} + \textcolor{grey}{x}\textcolor{orange}{a_3}
& &
\textcolor{grey}{\frac{1}{x}}\textcolor{orange}{a_2} + \textcolor{grey}{x}\textcolor{orange}{a_4}
\ \big] \\[6pt]
\big[ \
\textcolor{grey}{x}\textcolor{grey}{b_1} + \textcolor{grey}{\frac{1}{x}}\textcolor{grey}{b_3}
& &
\textcolor{grey}{x}\textcolor{grey}{b_2} + \textcolor{grey}{\frac{1}{x}}\textcolor{grey}{b_4}
\ \big] \\[10pt]
\big[ \
\textcolor{grey}{x}\textcolor{grey}{G_1} + \textcolor{grey}{\frac{1}{x}}\textcolor{grey}{G_3}
& &
\textcolor{grey}{x}\textcolor{grey}{G_2} + \textcolor{grey}{\frac{1}{x}}\textcolor{grey}{G_4}
\ \big]
\end{matrix}
\textcolor{orange}{z_{\textsf{next}}} :=
\langle \textcolor{orange}{\vec{a}_{\textsf{next}}}, \textcolor{grey}{\vec{b}_{\textsf{next}}} \rangle
\textcolor{lightgreen}{A_{\textsf{next}}} :=
\langle \textcolor{orange}{\vec{a}_{\textsf{next}}}, \textcolor{grey}{\vec{G}_{\textsf{next}}} \rangle
+
\textcolor{orange}{z_{\textsf{next}}} \cdot \textcolor{grey}{U}
\textcolor{lightgreen}{A}
\textcolor{grey}{x}
\big(
\textcolor{lightgreen}{L},
\textcolor{lightgreen}{R}
\big)
collapse
\textcolor{lightgreen}{A_{\textsf{next}}}
\stackrel{?}{=}
\textcolor{lightgreen}{A}
+
\textcolor{grey}{x^{-2}}\textcolor{lightgreen}{L}
+
\textcolor{grey}{x^{2}}\textcolor{lightgreen}{R}
\textcolor{orange}{\vec{a}_{\textsf{next}}}
\textcolor{lightgreen}{L} =
(\textcolor{orange}{a_1}
\textcolor{grey}{G_3}
+
\textcolor{orange}{a_2}
\textcolor{grey}{G_4})
+
(\textcolor{orange}{a_1}
\textcolor{grey}{b_3}
+
\textcolor{orange}{a_2}
\textcolor{grey}{b_4})
\textcolor{grey}{U}
\textcolor{lightgreen}{R} =
(\textcolor{orange}{a_3}
\textcolor{grey}{G_1}
+
\textcolor{orange}{a_4}
\textcolor{grey}{G_2})
+
(\textcolor{orange}{a_3}
\textcolor{grey}{b_1}
+
\textcolor{orange}{a_4}
\textcolor{grey}{b_2})
\textcolor{grey}{U}
IPA \(\longleftrightarrow\) Sumcheck
\big(
\textcolor{lightgreen}{L_1},
\textcolor{lightgreen}{R_1}
\big)
\textcolor{lightgreen}{A_1}
:=
\textcolor{lightgreen}{A}
\ + \
\textcolor{grey}{x_1^{-2}}\textcolor{lightgreen}{L_1}
\ + \
\textcolor{grey}{x_1^{2}}\textcolor{lightgreen}{R_1}
\big(
\textcolor{lightgreen}{L_2},
\textcolor{lightgreen}{R_2}
\big)
\textcolor{lightgreen}{A_2}
:=
\textcolor{lightgreen}{A_1}
\ + \
\textcolor{grey}{x_2^{-2}}\textcolor{lightgreen}{L_2}
\ + \
\textcolor{grey}{x_2^{2}}\textcolor{lightgreen}{R_2}
\big(
\textcolor{lightgreen}{L_n},
\textcolor{lightgreen}{R_n}
\big)
\vdots
\textcolor{lightgreen}{A_n}
:=
\textcolor{lightgreen}{A_{n-1}}
\ + \
\textcolor{grey}{x_n^{-2}}\textcolor{lightgreen}{L_n}
\ + \
\textcolor{grey}{x_n^{2}}\textcolor{lightgreen}{R_n}
\big(
\textcolor{orange}{a_n},
\textcolor{grey}{b_n}
\big)
\textcolor{lightgreen}{A_{n}}
\stackrel{?}{=}
\textcolor{orange}{a_n}\textcolor{grey}{G_n}
+
(\textcolor{orange}{a_n}\textcolor{grey}{b_n}) \cdot \textcolor{grey}{U}
\textcolor{grey}{x_2}
\textcolor{grey}{x_1}
\textcolor{grey}{x_3}
\textcolor{lightgreen}{g_1}(X)
\(v \stackrel{?}{=} g_1(0) + g_1(1)\)
\textcolor{grey}{r_1}
\(g_1(\textcolor{grey}{r_1}) \stackrel{?}{=} g_2(0) + g_2(1)\)
\textcolor{lightgreen}{g_2}(X)
\textcolor{grey}{r_2}
\(g_{n-1}(\textcolor{grey}{r_{n-1}}) \stackrel{?}{=} g_n(0) + g_n(1)\)
\textcolor{lightgreen}{g_{n}}(X)
\(g_{\mu}(\textcolor{grey}{r_{\mu}}) \stackrel{?}{=} f(\textcolor{grey}{r_1}, \textcolor{grey}{r_2}, \dots, \textcolor{grey}{r_\mu})\)
IPA is nice, but...
- IPA does not require trusted setups
- IPA strikes a reasonable middle-ground
- However, IPA verifier is \(\mathcal{O}(N)\)
Hash-based
Pairing-based
IPA-based
Field size
Proof size
\textcolor{lightgreen}{A}
+
\langle
\textcolor{grey}{\vec{x}_{\textsf{inv}}},
\textcolor{lightgreen}{\vec{L}}
\rangle
+
\langle
\textcolor{grey}{\vec{x}},
\textcolor{lightgreen}{\vec{R}}
\rangle
\ \stackrel{?}{=} \
\textcolor{orange}{a_n}\textcolor{grey}{G_n}
+
(\textcolor{orange}{a_n}\textcolor{grey}{b_n}) \cdot \textcolor{grey}{U}
\textcolor{lightgreen}{A_1}
:=
\textcolor{lightgreen}{A}
\ + \
\textcolor{grey}{x_1^{-2}}\textcolor{lightgreen}{L_1}
\ + \
\textcolor{grey}{x_1^{2}}\textcolor{lightgreen}{R_1}
\textcolor{lightgreen}{A_2}
:=
\textcolor{lightgreen}{A_1}
\ + \
\textcolor{grey}{x_2^{-2}}\textcolor{lightgreen}{L_2}
\ + \
\textcolor{grey}{x_2^{2}}\textcolor{lightgreen}{R_2}
\vdots
\textcolor{lightgreen}{A_n}
:=
\textcolor{lightgreen}{A_{n-1}}
\ + \
\textcolor{grey}{x_n^{-2}}\textcolor{lightgreen}{L_n}
\ + \
\textcolor{grey}{x_n^{2}}\textcolor{lightgreen}{R_n}
\textcolor{lightgreen}{A_{n}}
\ \stackrel{?}{=} \
\textcolor{orange}{a_n}\textcolor{grey}{G_n}
+
(\textcolor{orange}{a_n}\textcolor{grey}{b_n}) \cdot \textcolor{grey}{U}
IPA is nice, but...
- IPA does not require trusted setups
- IPA strikes a reasonable middle-ground
- However, IPA verifier is \(\mathcal{O}(N)\)
Hash-based
Pairing-based
IPA-based
Field size
Proof size
\textcolor{lightgreen}{A}
+
\langle
\textcolor{grey}{\vec{x}_{\textsf{inv}}},
\textcolor{lightgreen}{\vec{L}}
\rangle
+
\langle
\textcolor{grey}{\vec{x}},
\textcolor{lightgreen}{\vec{R}}
\rangle
\ \stackrel{?}{=} \
\textcolor{orange}{a_n}\textcolor{grey}{G_n}
+
(\textcolor{orange}{a_n}\textcolor{grey}{b_n}) \cdot \textcolor{grey}{U}
\underbrace{\hspace{5cm}}_{\textsf{logarithmic}}
\underbrace{\hspace{4cm}}_{\textsf{linear}}
- Halo showed a way to batch multiple IPA verifications
\begin{aligned}
\textcolor{grey}{G_n} =&\ (\textcolor{grey}{x_1^{-1} x_2^{-1} \dots x_n^{-1}}) \cdot \textcolor{grey}{G_1} \ + \ \\
&\ (\textcolor{grey}{x_1^{-1} x_2^{-1} \dots x_n^{+1}}) \cdot \textcolor{grey}{G_2} \ + \ \\
&\ \vdots \\
&\ (\textcolor{grey}{x_1^{+1} x_2^{+1} \dots x_n^{+1}}) \cdot \textcolor{grey}{G_N}.
\end{aligned}
\begin{aligned}
g(X, x_1, \dots, x_n) := \prod_{i=1}^{n} \left( x_i + x_i^{-1} \cdot X^{2^{i-1}} \right)
\end{aligned}
\begin{aligned}
\textcolor{grey}{G_n} := \textcolor{purple}{\textsf{commit}}(g(X, x_1, \dots, x_n))
\end{aligned}
IPA is nice, but...
\textcolor{lightgreen}{A}
+
\langle
\textcolor{grey}{\vec{x}_{\textsf{inv}}},
\textcolor{lightgreen}{\vec{L}}
\rangle
+
\langle
\textcolor{grey}{\vec{x}},
\textcolor{lightgreen}{\vec{R}}
\rangle
\ \stackrel{?}{=} \
\textcolor{orange}{a_n}\textcolor{grey}{G_n}
+
(\textcolor{orange}{a_n}\textcolor{grey}{b_n}) \cdot \textcolor{grey}{U}
\underbrace{\hspace{5cm}}_{\textsf{logarithmic}}
\underbrace{\hspace{4cm}}_{\textsf{linear}}
- Halo showed a way to batch multiple IPA verifications
\begin{aligned}
\textcolor{grey}{G_n} =&\ (\textcolor{grey}{x_1^{-1} x_2^{-1} \dots x_n^{-1}}) \cdot \textcolor{grey}{G_1} \ + \ \\
&\ (\textcolor{grey}{x_1^{-1} x_2^{-1} \dots x_n^{+1}}) \cdot \textcolor{grey}{G_2} \ + \ \\
&\ \vdots \\
&\ (\textcolor{grey}{x_1^{+1} x_2^{+1} \dots x_n^{+1}}) \cdot \textcolor{grey}{G_N}.
\end{aligned}
\begin{aligned}
g(X, x_1, \dots, x_n) := \prod_{i=1}^{n} \left( x_i + x_i^{-1} \cdot X^{2^{i-1}} \right)
\end{aligned}
\begin{aligned}
\textcolor{grey}{G_n} := \textcolor{purple}{\textsf{commit}}(g(X, x_1, \dots, x_n))
\end{aligned}
- Prover can send \(\textcolor{grey}{G_n}\) along with opening proof of \(g\)
- Prover can send \(\textcolor{grey}{G^{(1)}_n, G^{(2)}_n, \dots, G^{(m)}_n}\) along with respective opening proofs
- Verifier can batch-verify \(\implies\) one linear operation for \(m\) proofs
- This uses univariate PCS
Why care about IPA?
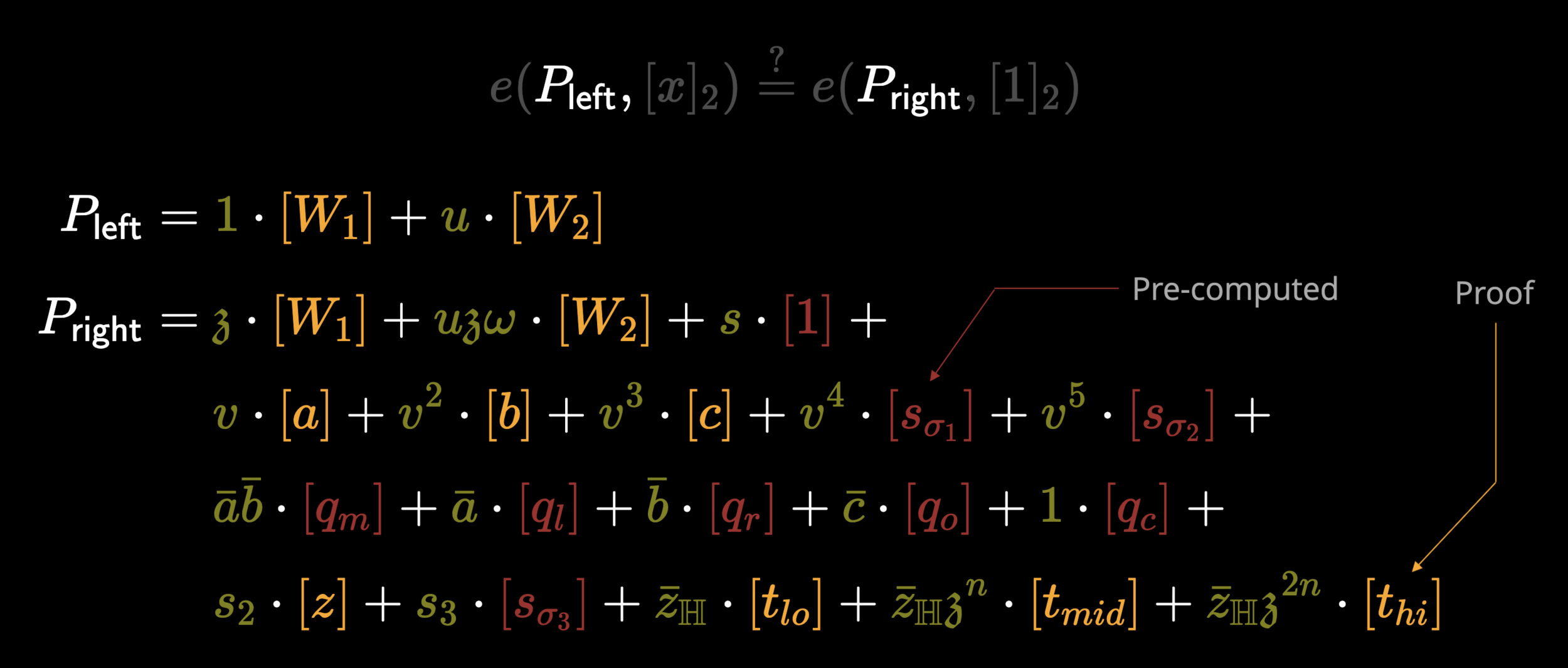
- Recursively verifying proofs requires non-native field arithmetic
- Using cycles of curves is one way to avoid non-native shenanigans
- BN254 \(\longleftrightarrow\) Grumpkin
- Grumpkin doesn't have pairings \(\implies\) use trustless proof system \(\implies\) IPA!
IPA as Sumcheck
- Polynomials over \(\mathbb{G}\): with coefficients \(\textcolor{grey}{A_1, \dots, A_N} \in \mathbb{G}\)
G(X) := \sum_{i=0}^{N-1} \textcolor{grey}{A_i} \cdot \textcolor{orange}{X^i}
- Two polynomial \(f, g\) over \(\mathbb{G}\) can be added as:
f(X) + g(X) := \sum_{i=0}^{N-1} (\textcolor{grey}{A_i + B_i}) \cdot \textcolor{orange}{X^i}
- For a multi-variate \(A(X_1, \dots, X_n) \in \mathbb{G}[X_1, \dots, X_n]\), round polynomial is:
A_i(X) := \sum_{b \in \mathfrak{B}_{n-i}} A(\textcolor{red}{r_1, \dots, r_{i-1}}, X, b)
IPA as Sumcheck
- For a multi-variate \(A(X_1, \dots, X_n) \in \mathbb{G}[X_1, \dots, X_n]\), round polynomial is:
A_i(X) := \sum_{b \in \mathfrak{B}_{n-i}} A(\textcolor{red}{r_1, \dots, r_{i-1}}, X, b)
- After the last round, the verifier outputs
\textcolor{red}{\bar{r}} = (\textcolor{red}{r_1, \dots, r_{n}})
v := A_n(\textcolor{red}{r_n})
\begin{matrix}
\textcolor{orange}{\vec{a}} =
\big[ \ \textcolor{orange}{a_1} & \textcolor{orange}{a_2} & \textcolor{orange}{a_3} & \textcolor{orange}{a_4} \ \big] \\[6pt]
\textcolor{grey}{\vec{b}} =
\big[ \ \textcolor{grey}{b_1} & \textcolor{grey}{b_2} & \textcolor{grey}{b_3} & \textcolor{grey}{b_4} \ \big] \\[7pt]
\textcolor{grey}{\vec{G}} = \big[ \ \textcolor{grey}{G_1} & \textcolor{grey}{G_2} & \textcolor{grey}{G_3} & \textcolor{grey}{G_4} \ \big]
\end{matrix}
\textcolor{lightgreen}{A} :=
\langle \textcolor{orange}{\vec{a}}, \textcolor{grey}{\vec{G}} \rangle +
\langle
\textcolor{orange}{\vec{a}},
\textcolor{grey}{\vec{b}}
\rangle
\cdot \textcolor{grey}{U}
- Lets recall IPA setup:
\textcolor{lightgreen}{A}(\textcolor{grey}{X_1, \dots, X_n}) :=
\textcolor{orange}{f}(\textcolor{grey}{\mathbf{X}})
\textcolor{grey}{G}(\textcolor{grey}{\mathbf{X}})
+
\textsf{eq}(\textcolor{grey}{\mathbf{X}}, \textcolor{grey}{\bar{b}})
\textcolor{orange}{f}(\textcolor{grey}{\mathbf{X}})
\cdot \textcolor{grey}{U}
IPA as Sumcheck
\begin{matrix}
\textcolor{orange}{\vec{a}} =
\big[ \ \textcolor{orange}{a_1} & \textcolor{orange}{a_2} & \textcolor{orange}{a_3} & \textcolor{orange}{a_4} \ \big] \\[6pt]
\textcolor{grey}{\vec{b}} =
\big[ \ \textcolor{grey}{b_1} & \textcolor{grey}{b_2} & \textcolor{grey}{b_3} & \textcolor{grey}{b_4} \ \big] \\[7pt]
\textcolor{grey}{\vec{G}} = \big[ \ \textcolor{grey}{G_1} & \textcolor{grey}{G_2} & \textcolor{grey}{G_3} & \textcolor{grey}{G_4} \ \big]
\end{matrix}
\textcolor{lightgreen}{A} :=
\langle \textcolor{orange}{\vec{a}}, \textcolor{grey}{\vec{G}} \rangle +
\langle
\textcolor{orange}{\vec{a}},
\textcolor{grey}{\vec{b}}
\rangle
\cdot \textcolor{grey}{U}
- Lets recall IPA setup:
\textcolor{lightgreen}{A}(\textcolor{grey}{X_1, \dots, X_n}) :=
\textcolor{orange}{f}(\textcolor{grey}{\mathbf{X}})
\textcolor{grey}{G}(\textcolor{grey}{\mathbf{X}})
+
\textsf{eq}(\textcolor{grey}{\mathbf{X}}, \textcolor{grey}{\bar{b}})
\textcolor{orange}{f}(\textcolor{grey}{\mathbf{X}})
\cdot \textcolor{grey}{U}
- Prover runs sumcheck on \(\textcolor{lightgreen}{A}(\textcolor{grey}{X_1, \dots, X_n})\)
- After last round, the verifier outputs: \(\textcolor{red}{\bar{r}} \in \mathbb{F}^n\) and \(V = A_n(\textcolor{red}{r_n}) \in \mathbb{G}\)
- Final verifier check:
V \stackrel{?}{=}
\textcolor{orange}{f}(\textcolor{red}{\bar{r}}) \cdot \textcolor{grey}{G}(\textcolor{red}{\bar{r}})
+
\textcolor{grey}{\textsf{eq}(\textcolor{grey}{\bar{b}}, \textcolor{red}{\bar{z}})}
\textcolor{orange}{f}(\textcolor{red}{\bar{r}})
\cdot \textcolor{grey}{U}
prover sends
verifier can compute
- Instead of evaluating \(\textcolor{grey}{G},\) verifier outputs:
\left(\textcolor{red}{\bar{r}}, \ \frac{V - \textcolor{grey}{\textsf{eq}(\textcolor{grey}{\bar{b}}, \textcolor{red}{\bar{z}})}
\textcolor{orange}{f}(\textcolor{red}{\bar{r}}) \cdot U}{\textcolor{orange}{f}(\textcolor{red}{\bar{r}})} \right)
Accumulate
- Suppose we have multiple instances:
\big(\textcolor{red}{\bar{r}_1}, C_1 \big), \
\big(\textcolor{red}{\bar{r}_2}, C_2 \big), \
\dots \ , \
\big(\textcolor{red}{\bar{r}_m}, C_m \big)
- Ideally, we know that each \(C_j = \textcolor{grey}{G}(\textcolor{red}{\bar{r}_j})\) for all \(j \in [m]\)
- To prove this, we compute the linear combination
C := \sum_{j\in[m]}^{} \textcolor{red}{\gamma^j} \cdot C_j
- And define the sumcheck instance as:
A(\textcolor{grey}{\mathbf{X}})
:=
\textcolor{grey}{G}(\textcolor{grey}{\mathbf{X}})
\cdot
E(\textcolor{grey}{\mathbf{X}})
E(\textcolor{grey}{\mathbf{X}})
=
\sum_{j\in[m]}
\textcolor{red}{\gamma^j} \textsf{eq}(\textcolor{grey}{\mathbf{X}}, \textcolor{red}{\bar{r}_j})
s.t.
- The verifier can output:
\left(\textcolor{red}{\bar{r}}, \ \frac{V}{E(\textcolor{red}{\bar{r}})} \right)
Decide
- Finally, given \(\big(\textcolor{red}{\bar{r}}, C \big)\) the verifier needs to check
A(\textcolor{grey}{\mathbf{X}})
:=
\textcolor{grey}{G}(\textcolor{grey}{\mathbf{X}})
\cdot
\textsf{eq}(\textcolor{grey}{\mathbf{X}}, \textcolor{red}{\bar{r}})
C = \textcolor{grey}{G}(\textcolor{red}{\bar{r}})
- Again, define a sumcheck instance
- Use BaseFold to prove multi-linear evaluation: just like MLE PCS over fields, but now over group!
- Can also use Yuval's optimisation instead of basefold
Summary
- Simpler halo-style accumulation that works for MLE evaluation claims
- Size-\(N\) MSM by IPA verifier can be replaced by
- "group" variant of basefold
- reduces verifier from \(\mathcal{O}(N)\) to \(\mathcal{O}(\text{log}^2(N))\)
- prover cost increases only by \(4N\) scalar muls
Sumcheck-IPA Connection
By Suyash Bagad
Sumcheck-IPA Connection
- 84



