競技程式設計

Competitive Programming

Guild line

  • 上課時間：19:00 ~ 20:00
  • 上課地點：台達館，看哪間教室亮著
  • 對象：想加強程式設計能力的同學
  • 功課：有題單，自行完成

助教資訊

李旺陽、日月卦長、盧振華

 

TA Room : 資電 124 （助教室）

 

競技程式有關比賽報名、帶隊、規劃比賽

培訓教學 etc

 

 

重要行程

  • 上學期
    • NCPC 初賽
    • NCPC 決賽
    • ICPC 台灣站
    • ICPC 海外站
    • 上學期校內體驗賽 (期末)
  • 下學期
    • ICPC WF
    • 台清交程式競賽
    • 校內程式個人賽
    • 兩岸清華

For beginner

  • 多練習
    • 不僅是解出題目，還要改進自己的程式風格
       
  • 多查資料
    • 演算法筆記 etc.
    • 不要輕易相信別人的答案，要驗證
       
  • 多問 TA、學長、同學

Special Format Input

scanf / sscanf / stringstream

Special Format Input

有時會需要讀入不是用空白換行隔開的資料

2019/09/22

12:35

Hint 1. 當作字串讀取後，再利用字串的技巧取出資料

Hint 2. 利用 scanf 來在輸入時處理

UVa 579 Clockhands

Input

12:00
9:00
8:10
0:00
Output

0.000
90.000
175.000

UVa 11219 How old are you

Input

4

01/01/2007

12/02/2007

09/06/2007

28/02/1871

Output

Case #1: Invalid birth date

Case #2: Check brith date

互斥集

https://slides.com/sylveon/cp2019-spring#/4

二分搜尋法

https://slides.com/sylveon/cp2019-spring#/3

Recursive

Power

$$a^b$$

int ans = 1;
for(int i=1;i<=b;++i)
    ans = ans * a;

Power

考慮去掉最後一個元素 與 原來問題的差異

\(a^b=a\times a \times a \cdots \times a \times a\)

\(=(a\times a \times a \cdots \times a )\times a\)

\(=a^{b-1}\times a\)

去掉一個 \(a\) 問題會變什麼

如果原來有很多 \(a\)

\(=a^{b-1}\times a\)

如果只有 1 個 \(a\)

\(=1 \times a\)

如果沒有 \(a\)

\(=1/a \times a\)  🤔

\(=1\) 😀

邊界選擇不一定唯一

但是盡量避免衍伸太多的例外

int pow(int a, int e) {
    if (e == 0)
        return 1;

    return a * pow(a, e-1);
}

Reuse

\(a^b=a\times a \times a \cdots \times a \times a\)

\(a^b=a^ka^ka^{b-2k}\)

不僅是讓問題變小

也讓小問題能夠重複被利用

Reuse

\(a^b=a^ka^ka^{b-2k}\)

不僅是讓問題變小

也讓小問題能夠重複被利用

\(a^k\)

\(a^k\)

\(a^{b-2k}\)

只會是 a 或是 1

\(k=b/2\)

int pow(int a, int e) {
    if ( e == 0 )
    	return 1;
        
    int val = pow (a, e/2);
    
    val *= val;
    if ( e%2==1 )
        val *= a;
    
    return val;
}

more idea...

  • Binary Encoding

\(a^b=a^0 a^1 a^2a^4a^8\cdots\)

int pow(int a, int e) {
    int ans = 1;
    int pw = a;
    
    for (int i=0;i<32;++i) {
    	if (e & (1<<i))
            ans *= pw;

        pw *= pw; 
    }
    
    return ans;
}

Tiling - UVA 10359

考慮去掉最後一個元素 與 原來問題的差異

考慮去掉最後一個元素 與 原來問題的差異

Coin Change

在某一個國家流通了 \(a_1,a_2,a_3,\cdots,a_n\) 共 \(n\) 種面額的貨幣

保證有 1 元的面額

  • 求 付出 \(k\) 元不找零有幾種方法

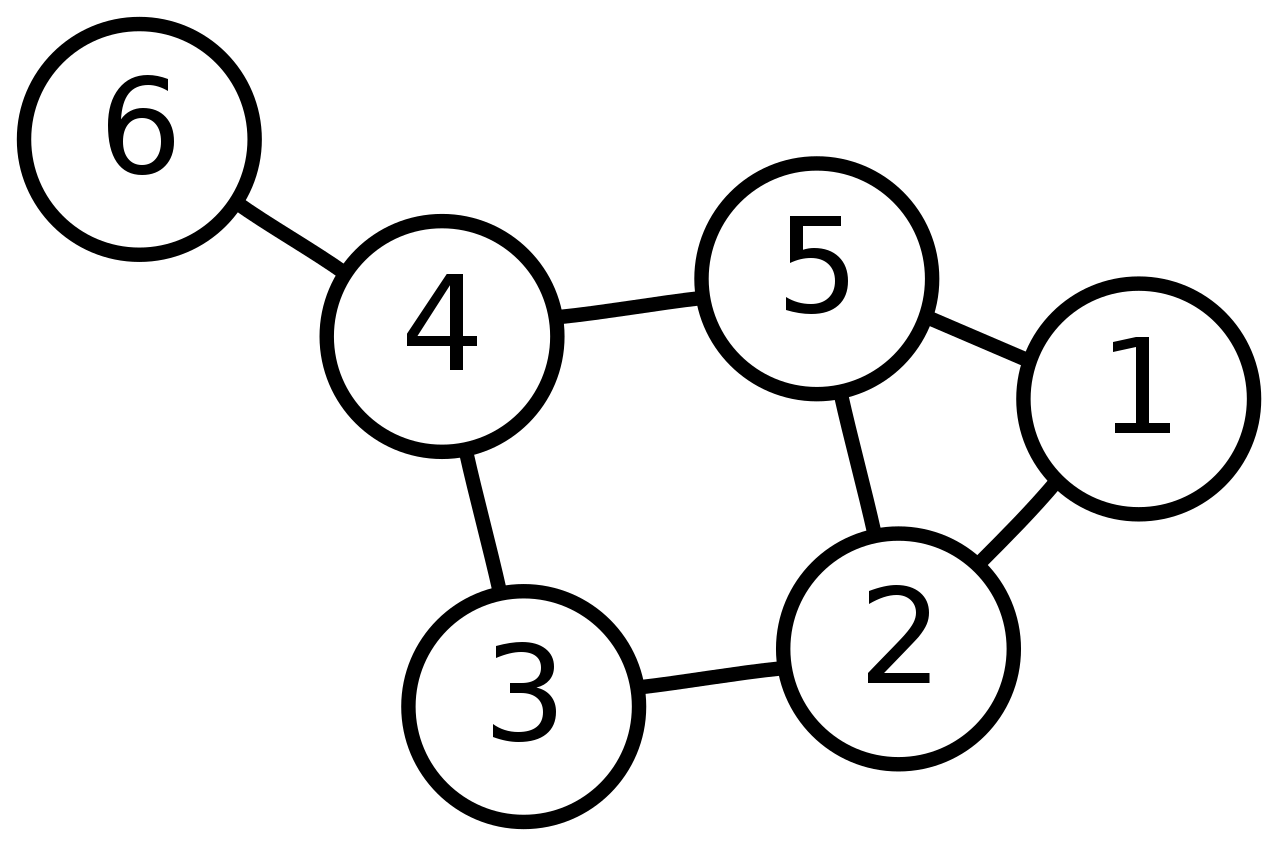
Graph

圖論

This is Image

This is Garph

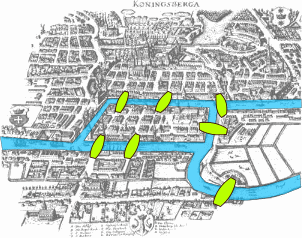
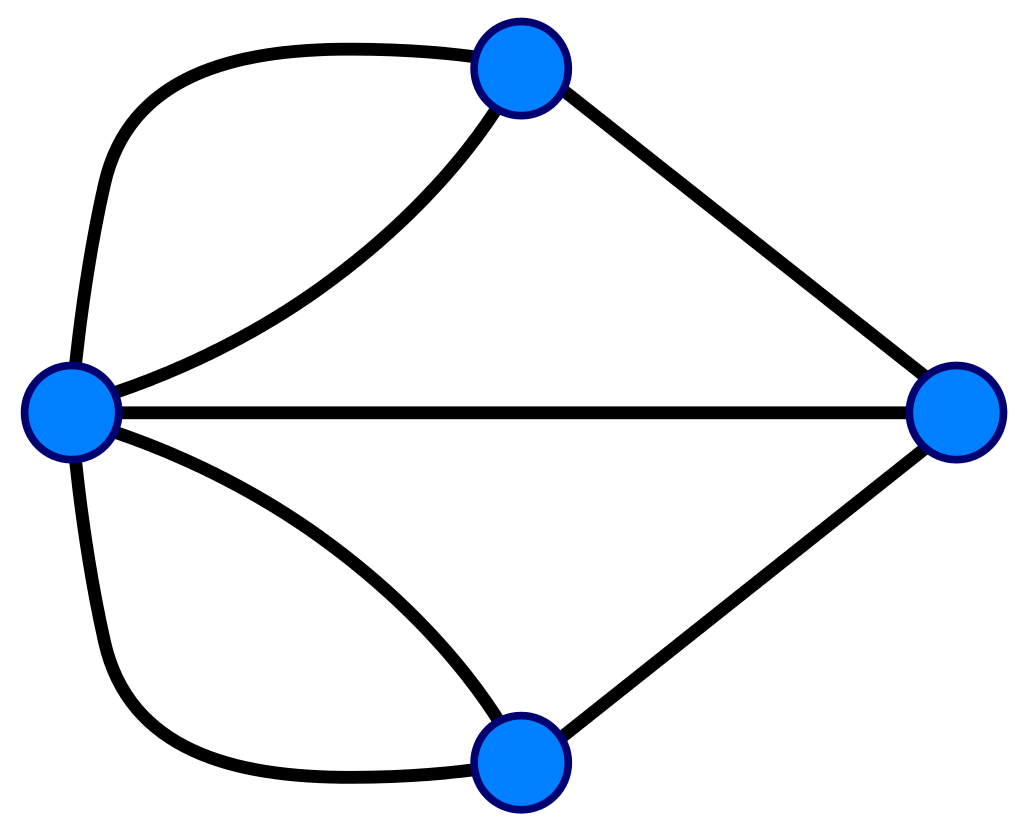
七橋問題

Graph

  • 一張圖 Graph 是討論

點 Vertex 

邊 Edge ( 點之間的關聯 )

的學問

Graph

  • 一般而言，因為圖論的專有名詞沒有"精巧的"中文翻譯，所以學習時務必對於英文名詞孰悉
英文(n.) 中譯(參考某知名書籍)
walk 道路
path 路徑
trail 行跡
tour 迴路

Coloring

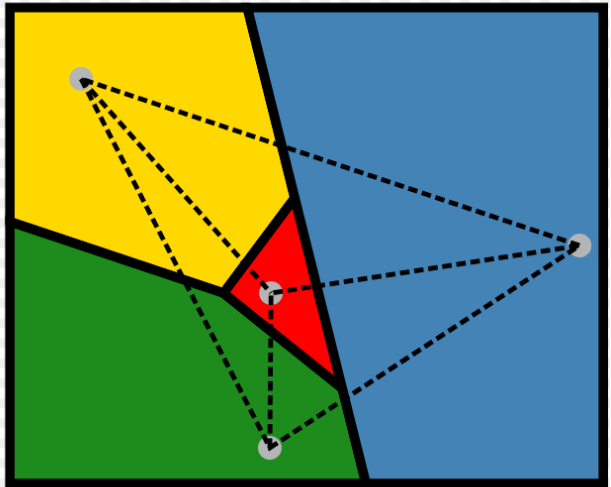
給定一張地圖

 

如果希望一個區域與相鄰的區域有不同的顏色

那最少要幾種顏色？

Note.

假設地圖是一個平面，無飛地

Coloring

如何討論怎麼著色?

 

一個區塊有很多形狀

 

不同形狀能銜接的鄰居都不一樣...

 

枚舉所有的形狀 ?

Coloring

著色問題

 

一個區塊雖然有很多形狀

 

但答案比起區塊的形狀

 

討論區塊可能的相連方法比較重要

Coloring

著色問題

 

一個區塊雖然有很多形狀

 

但答案比起區塊的形狀

 

討論區塊可能的相連方法比較重要

  • 一張圖 Graph 是討論

點 Vertex 

邊 Edge ( 點之間的關聯 )

的學問

Coloring

  • 一張圖 Graph 是討論

點 Vertex 

邊 Edge ( 點之間的關聯 )

的學問

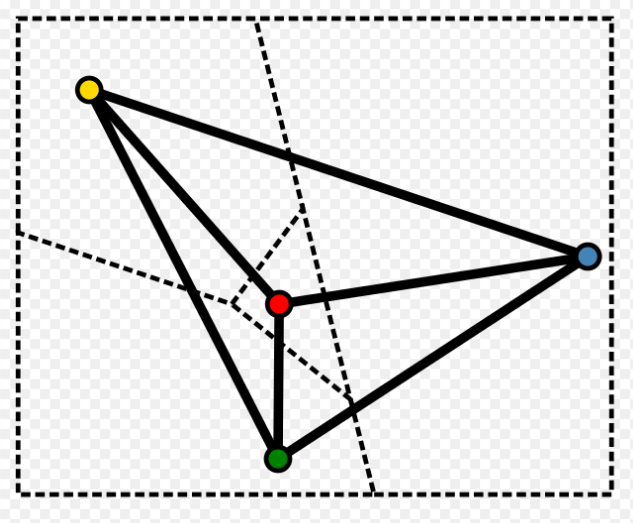
Coloring

  • 一張圖 Graph 是討論

點 Vertex 

邊 Edge ( 點之間的關聯 )

的學問

Coloring

  • 一張圖 Graph 是討論

點 Vertex 

邊 Edge ( 點之間的關聯 )

的學問

點著色問題

 

每一個點都要有顏色

相鄰的點顏色要不一樣

 

至少要幾個顏色才能滿足條件

Graph

  • 圖的結構
  • 要怎麼在程式中紀錄一張圖呢 ?

1

2

3

4

Graph

  • 二維陣列：用 a[i][j] 來記錄點 \(i\) 到點 \(j\) 有沒有邊
  • 根據題目要求決定 a[i][i] 的值是多少

1

2

3

4

1 2 3 4
1 1 1 1
2 1
3 1 1
4 1 1

Graph

  • 連接串列：對於每一個點，只紀錄他的鄰居有誰

1

2

3

4

vector<int> V[4];

//V[i] 儲存 點 i 的鄰居有誰
V[3] = {1,4};

Graph

  • 邊陣列：把邊資料存成一個陣列
  • 不能直接知道一個點的鄰居，但可以結合連接串列使用 
struct Edge {
    int s;
    int e;
} edge[100];

1

2

3

4

Coloring

點著色問題

 

檢查一張圖(平面的)是否可以用 \(K\) 種顏色塗色，使得相鄰的點顏色不同

\(K = 1\)

有邊就不行

\(K = 2\)

easy algo.

\(K = 3\)

NP Problem

\(K = 4\)

四色定理

1996. NEIL ROBERTSON \(O(v^2)\)

Bicoloring (uva 10004)

檢查一張圖是否可以用 \(2\) 種顏色塗色，使得相鄰的點顏色不同

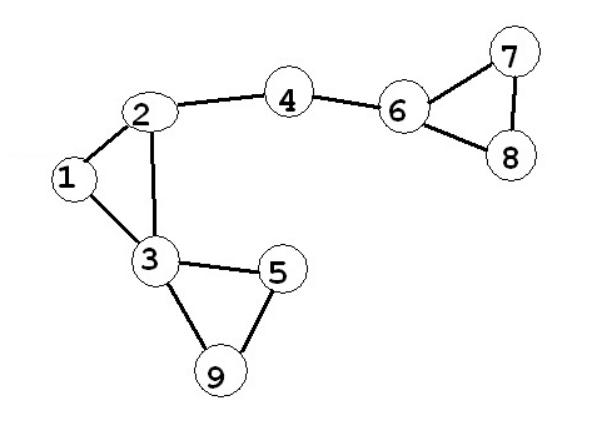
Bicoloring (uva 10004)

檢查一張圖是否可以用 \(2\) 種顏色塗色，使得相鄰的點顏色不同

決定好一個點的顏色之後，他鄰居的顏色就被固定了

Bicoloring (uva 10004)

檢查一張圖是否可以用 \(2\) 種顏色塗色，使得相鄰的點顏色不同

1. 決定一個點的顏色

 

 

        

 

Bicoloring (uva 10004)

檢查一張圖是否可以用 \(2\) 種顏色塗色，使得相鄰的點顏色不同

1. 決定一個點的顏色

2. 檢查這一個點的鄰居

      如果還沒有顏色，就幫他塗

        

 

Bicoloring (uva 10004)

檢查一張圖是否可以用 \(2\) 種顏色塗色，使得相鄰的點顏色不同

1. 決定一個點的顏色

2. 檢查這一個點的鄰居

      如果還沒有顏色，就幫他塗

      如果有顏色，就檢查是否合法  

 

Bicoloring (uva 10004)

檢查一張圖是否可以用 \(2\) 種顏色塗色，使得相鄰的點顏色不同

1. 決定一個點的顏色

2. 檢查這一個點的鄰居

      如果還沒有顏色，就幫他塗

      如果有顏色，就檢查是否合法  

3. 改以鄰居為出發點 (遞迴2.)

Bicoloring (uva 10004)

檢查一張圖是否可以用 \(2\) 種顏色塗色，使得相鄰的點顏色不同

1. 決定一個點的顏色

2. 檢查這一個點的鄰居

      如果還沒有顏色，就幫他塗

      如果有顏色，就檢查是否合法  

3. 改以鄰居為出發點 (遞迴2.)

Bicoloring (uva 10004)

檢查一張圖是否可以用 \(2\) 種顏色塗色，使得相鄰的點顏色不同

1. 決定一個點的顏色

2. 檢查這一個點的鄰居

      如果還沒有顏色，就幫他塗

      如果有顏色，就檢查是否合法  

3. 改以鄰居為出發點 (遞迴2.)

Bicoloring (uva 10004)

檢查一張圖是否可以用 \(2\) 種顏色塗色，使得相鄰的點顏色不同

1. 決定一個點的顏色

2. 檢查這一個點的鄰居

      如果還沒有顏色，就幫他塗

      如果有顏色，就檢查是否合法  

3. 改以鄰居為出發點 (遞迴2.)

Bicoloring (uva 10004)

檢查一張圖是否可以用 \(2\) 種顏色塗色，使得相鄰的點顏色不同

1. 決定一個點的顏色

2. 檢查這一個點的鄰居

      如果還沒有顏色，就幫他塗

      如果有顏色，就檢查是否合法  

3. 改以鄰居為出發點 (遞迴2.)

Bicoloring (uva 10004)

檢查一張圖是否可以用 \(2\) 種顏色塗色，使得相鄰的點顏色不同

1. 決定一個點的顏色

2. 檢查這一個點的鄰居

      如果還沒有顏色，就幫他塗

      如果有顏色，就檢查是否合法  

3. 改以鄰居為出發點 (遞迴2.)

圖的走訪

  • 按照某種順序看過一張圖上的所有點

通常一個點只會看一次

 

  • 比起從 1 號點 2 號點這樣檢查，通常檢查一個點的鄰居比較有用

圖的走訪 - DFS

Depth-First Search 深度優先搜尋

void dfs(int v)
{
    used[v] = true; // 看過 v 號點
    
    for (int next : V[v]) // v 的所有鄰居
    {
    	if (!used[next])
            dfs(next);
    }
}

如果有看到沒看過的鄰居，就走進去

圖的走訪 - DFS

Depth-First Search 深度優先搜尋

思考策略：站在一個點上想事情
 

仔細思考如果鄰居是有走過的，還是沒走過的，分別怎麼處理，再計算答案。

圖的走訪 - DFS

Depth-First Search 深度優先搜尋

DFS 相當於把鄰居放進一個 Stack 裡面逐一存取

stack<int> st;
st.push(0); // 放入起始點
used[0] = true;

while (!st.empty())
{
    int v = st.top();
    st.pop();
    
    for (int next:V[v])
        if (!used[next])
        {
            used[next] = true;
            st.push(next);
        }
}

圖的走訪 - BFS

Breadth-First Search 廣度優先搜尋

BFS 相當於把鄰居放進一個 Queue 裡面逐一存取

queue<int> st;
st.push(0); // 放入起始點
used[0] = true;

while (!st.empty())
{
    int v = st.front();
    st.pop();
    
    for (int next:V[v])
        if (!used[next])
        {
            used[next] = true;
            st.push(next);
        }
}

圖的走訪 - BFS

Breadth-First Search 廣度優先搜尋

BFS 相當於把鄰居放進一個 Queue 裡面逐一存取

使用 BFS 的方法拿點，會從距離起點最近的點逐漸達到距離起點最遠的點 (why?)

利用此性質可以用來解決一些最短路徑問題 (需要邊長一致)

圖的走訪 - BFS

Breadth-First Search 廣度優先搜尋

ZJ a290ž

UVa193

žUva 10004

ž

žDFS/BFS練習

žUVa441

žUVa11352

žUVa11513

žUVa11730

žUVa12101

Hash

雜湊

Hash

  • 透過某種函數，為資料建立特徵的方法
  • 一般而言，特徵的資料量會比原始資料小，因此能用於加速計算

Raw

HashCode

Hash

Hash

  • 設雜湊函數為 \(H(x)=h\)
  • 如果有 \(x\neq y\)，但是\(H(x)=H(y)\) 稱為雜湊的碰撞
  • 能維持雜湊的碰撞率低，且輸出資料量仍舊小的 \(H\) 越好

Raw

HashCode

Hash

常見的雜湊

Input Output 發現碰撞
MD5 inf 128 Yes
SHA-1 2^64-1 160 Yes
SHA-512 2^128-1 512 等你發現

https://www.ithome.com.tw/news/112347

雜湊的應用

  • C++ 內建的 unordered_set / unordered_set 

unordered_set

unordered_set<int> ust;
	
ust.insert(71);
ust.insert(22);
	
if (ust.find(22) == ust.end()) // true
    cout << "22 is found\n"; 
	
ust.erase(71);  // delete element
	
if (ust.find(71) == ust.end()) // false
    cout << "71 is found\n";

可以在平均 O(1) 的時間

加入/刪除/調查元素

unordered_map

unordered_map<string, int> ump;

ump["one"] = 1;
ump["two"] = 2;
ump["three"] = 3;

//123
cout << ump["one"] << ump["two"] << ump["three"];

可以在平均 O(1) 的時間

加入/刪除/調查元素

把 map 當作是 index 可以自定義型態的超強陣列就對了

自定義雜湊

  • 由於自定義雜湊的寫法需要更多 C++ 語法知識
  • 待各位學習完C++後自行研究
namespace std
{
    template<> struct hash<S>
    {
        std::size_t operator()(S const& s) const noexcept
        {
            std::size_t h1 = std::hash<std::string>{}(s.first_name);
            std::size_t h2 = std::hash<std::string>{}(s.last_name);
            return h1 ^ (h2 << 1);
        }
    };
}

Rabin fingerprint

滾動雜湊

Rabin fingerprint

  • 一般而言，雜湊常用於字串比對，以 strcmp 為例
  • 單純的字串比較需要 \(O(|S_1|+|S_2|)\) 
  • 如果有 \(k\) 個字串要檢查，會需要 \(O(|S|\times\Sigma|S_i|)\)

如果能先將字串透過萃取成一個 int ， 那只需要 \(O(1\times\Sigma{|S|})\) 的時間

Rabin fingerprint

  • Rabin fingerprint 是一個很簡單的雜湊函數
     
  • 如果字串 \(S=a_1a_2a_3a_4\dots a_n\)
     
  • \(H(S,x)=a_1x^{n-1}+a_2x^{n-2}+a_3x^{n-3}+\dots+a_nx^0\)
  • 一般而言，會取 H(S,x) 除以 p 的餘數，x,p 必須互質

Rabin fingerprint

  • 如果字串 \(S=a_1a_2a_3a_4\dots a_n\)
  • \(H(S,x)=a_1x^{n-1}+a_2x^{n-2}+a_3x^{n-3}+\dots+a_nx^0\)

 

  • 如果字串 \(S'=a_1a_2a_3a_4\dots a_na_{n+1}\)
  • \(H(S',x)\\=a_1x^{n}+a_2x^{n-1}+a_2x^{n-3}+\dots+a_nx^1+a_{n+1}x^0\\=xH(S,x)+a_{n+1}\)

Rabin fingerprint

#define MAXN 1000000
#define prime_mod 1073676287
/*prime_mod 必須要是質數*/
typedef long long T;
char s[MAXN+5];
T h[MAXN+5];/*hash陣列*/
T h_base[MAXN+5];/*h_base[n]=(prime^n)%prime_mod*/
inline void hash_init(int len,T prime=0xdefaced){
	h_base[0]=1;
	for(int i=1;i<=len;++i){
		h[i]=(h[i-1]*prime+s[i-1])%prime_mod;
		h_base[i]=(h_base[i-1]*prime)%prime_mod;
	}
}

Rabin fingerprint

Rabin fingerprint 具有滾動的性質，如果知道每一個前綴的 Hash，很容易可以推算中間任意一段的 Hash

\(S'=a_La_{L+1}a_{L+2}\dots+a_R\)

求\(H(S',x)=a_Lx^{R-L}+a_{L+1}x^{R-L-1}+\dots+a_Rx^0\)

Rabin fingerprint

\(S'=a_La_{L+1}a_{L+2}\dots+a_R\)

求\(H(S',x)=a_Lx^{R-L}+a_{L+1}x^{R-L-1}+\dots+a_Rx^0\)

\(S_R=a_1a_2a_3\dots+a_R\)

\(H(S_R,x)=a_1x^{R-1}+a_2x^{R-2}+\dots+a_{L-1}x^{R-L+1}+a_{L}x^{R-L}+\dots+a_Rx^0\)

\(S_{L-1}=a_1a_2a_3\dots+a_{L-1}\)

\(H(S_{L-1},x)=a_1x^{L-2}+a_2x^{L-3}+\dots+a_{L-1}x^{0}\)

Rabin fingerprint

\(S'=a_La_{L+1}a_{L+2}\dots+a_R\)

求\(H(S',x)=a_Lx^{R-L}+a_{L+1}x^{R-L-1}+\dots+a_Rx^0\)

\(S_R=a_1a_2a_3\dots+a_R\)

\(H(S_R,x)=a_1x^{R-1}+a_2x^{R-2}+\dots+a_{L-1}x^{R-L+1}+a_{L}x^{R-L}+\dots+a_Rx^0\)

\(S_{L-1}=a_1a_2a_3\dots+a_{L-1}\)

\(H(S_{L-1},x)=a_1x^{L-2}+a_2x^{L-3}+\dots+a_{L-1}x^{0}\)

\(H(S',x)=H(S_R,x)-x^{R-L+1}H(S_{L-1},x)\)

inline T get_hash(int l,int r){
    return (h[r+1]
        -(h[l]*h_base[r-l+1])
            %prime_mod+prime_mod)
        %prime_mod;
}

文本匹配問題

有一本書，當作是字串 S

想問一個單字 T 在這本書裡面出現幾次

文本匹配問題

暴力法 \(O(|S||T|)\)

 

\(S=\text{aaaaaaaaaaaaaaaaaaaaaaaaaa}\)

\(T=\text{aaaab}\)

文本匹配問題

KMP Algorithm \(O(|S|+|T|)\)

 

修演算法再頭痛吧 (比賽還是要會)

文本匹配問題

Rabin–Karp Algorithm \(O(|S|+|T|)\)

 

雜湊唬爛法

計算 S 所有前綴的雜湊 \(O(S)\)

計算 T 的雜湊 \(O(T)\)

檢查 S 中所有長度為 \(|T|\) 的字串，雜湊是否與 T 相同 \(O(S)\) 

Rabin fingerprint

碰撞率，若 H(S,x) 中 x 夠大，那碰撞率為 1/p

換句話說只跟取的餘數有關係

如果進行 k 次比較，希望有 50 % 的正確率， p 要多大?

Rabin fingerprint

如果進行 k 次比較，希望有 50 % 的正確率， p 要多大?

\((1-1/p)^k\geq 0.5\)

\(1-1/p\geq 0.5^{1/k}\)
\(p\geq 1/(1- 0.5^{1/k})\)

int 不夠大怎麼辦?  算多個雜湊一起比較!

nthucp2019

By sylveon

Made with Slides.com

nthucp2019

  • 1,436

More from sylveon