Math Skill

定義與假設

如果沒有特別說明，討論的變數定義範圍是 0 或正整數 $\N_0$

定義與假設

如果有出現 pow ，指的是快速冪

ll qpow(ll a, ll e)
{
    ll res = 1;
    
    while( e )
    {
        if( e&1 ) res = res * a % mod;
        e/=2;
        a=a*a%mod;
    }
    return res;
}

快速冪

沒事別用 pow @

如果要計算整數的整數次方，盡量不要使用 pow
```
pow(x,2) 比 x*x 還要慢 2.5 倍
```
```
pow(x,3) 比 x*x*x 還要慢 100 倍
```
C/C++ 內建的 pow 是基於小數運算的，還會有浮點誤差
- ```
pow(1.5, 0.7)
```

快速冪

exponentiating by squaring
平方求冪法

有效率的計算整數冪次： $a^e$

如果 $e$ 太大，就把它砍一半

$a^e=\left(a^{e/2}\right)^2$

快速冪

$a^e=\left(a^{e/2}\right)^2$

$a^e=$

$1~~~~~\text{if } e = 0$

$(a^{e/2})^2~~~~\text{if } e $ 是偶數

$a\cdot (a^{\lfloor e/2\rfloor})^2~~~~\text{if } e $ 是奇數

一般而言 $a^e$ 的數值非常大，因此經常會取其處以 $m$ 的餘數

一般而言 $a^b$ 的數值非常大，因此經常會取其處以 $m$ 的餘數

int qpow(int a, int e, int m) {
    if (e == 0)
        return 1;
    
    int x = qpow(a, e/2, m);
    
    x = x * x % m;
    if (e % 2 == 1)
        x = x * a % m;
    
    return x;
}

小心 $m=1$

bang!

迴圈版

效率比較好

int qpow(int a, int e, int m) {
    int res = 1;

    while (e) {
        if (e & 1) res = res * a % m;
        e /= 2;
        a = a * a % m;
    }

    return res;
}

事實上，這跟 python ** 的實作一樣@

時間複雜度

很明顯的 $O(\log {e})$， $e$ 是 $a^e$ 指數的部分

矩陣快速冪

不僅一般數字的冪次可以折半再平方
矩陣的的冪次也可以折半再平方
- $M^b=\left(M^{b/2}\right)^2$

費式數列

$F_0=0$
$F_1=1$
$F_n=F_{n-1}+F_{n-2}$

$0,1,1,2,3,5,8,13,21,\cdots$

for (int i=2;i<=n;++i)
    F[i] = F[i-1] + F[i-2];

任意項費事數列

原來的演算法從第 $1$ 項逐一累加到最後一項
- 時間複雜度 $O(n)$
若 $n$ 過大 (long long 範圍)，就需要更快的求法 !

a_{{n}}={\frac {{\sqrt {5}}}{5}}\cdot \left[\left({\frac {1+{\sqrt {5}}}{2}}\right)^{{n}}-\left({\frac {1-{\sqrt {5}}}{2}}\right)^{{n}}\right]

透過一般式，雖然可以用快速冪，但計算會有誤差 (又很難記)

任意項費事數列

線性代數解法

找出一個矩陣 $M$ ，使得 $f_n$ 乘上矩陣後，可以獲得 $f_{n+1}$

{\begin{bmatrix} & \\ \text{ } & \text{ } \end{bmatrix}}

{\begin{bmatrix} f_n \\ \text{ } \end{bmatrix}}

{\begin{bmatrix} f_{n+1} \\ \text{ } \end{bmatrix}}

任意項費事數列

{\begin{bmatrix} & \\ \text{ } & \text{ } \end{bmatrix}}

{\begin{bmatrix} f_n \\ \text{ } \end{bmatrix}}

{\begin{bmatrix} f_{n+1} \\ \text{ } \end{bmatrix}}

\times

$F_n=F_{n-1}+F_{n-2}$

任意項費事數列

{\begin{bmatrix} 1 & 1 \\ \text{ } & \text{ } \end{bmatrix}}

{\begin{bmatrix} f_n \\ f_{n-1} \end{bmatrix}}

{\begin{bmatrix} f_{n+1} \\ \text{ } \end{bmatrix}}

\times

$F_n=F_{n-1}+F_{n-2}$

任意項費事數列

{\begin{bmatrix} 1 & 1 \\ \text{ } & \text{ } \end{bmatrix}}

{\begin{bmatrix} f_n \\ f_{n-1} \end{bmatrix}}

{\begin{bmatrix} f_{n+1} \\ f_{n} \end{bmatrix}}

\times

$F_n=F_{n-1}+F_{n-2}$

任意項費事數列

{\begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}}

{\begin{bmatrix} f_n \\ f_{n-1} \end{bmatrix}}

{\begin{bmatrix} f_{n+1} \\ f_{n} \end{bmatrix}}

\times

$F_n=F_{n-1}+F_{n-2}$

任意項費事數列

{\begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}}

{\begin{bmatrix} f_n \\ f_{n-1} \end{bmatrix}}

{\begin{bmatrix} f_{n+1} \\ f_{n} \end{bmatrix}}

$F_n=F_{n-1}+F_{n-2}$

任意項費事數列

{\begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}}^n

{\begin{bmatrix} f_1 \\ f_{0} \end{bmatrix}}

{\begin{bmatrix} f_{n+1} \\ f_{n} \end{bmatrix}}

$F_n=F_{n-1}+F_{n-2}$

快速冪!

線性遞迴式

任意類似 $F_n=aF_{n-1}+bF_{n-2}+\cdots$ 的遞迴關係

皆可使用矩陣快速冪方法完成

是重要的加速技巧 !

problems.pdf (twpca.org)

Ranking (sorahisa.github.io)

using matrix = vector<vector<int>>;

const matrix I2 = {
    {1, 0},
    {0, 1}};

matrix mul(const matrix &a, const matrix &b, int mod) {
    matrix c(a.size(), vector<int>(b[0].size()));

    for (size_t i = 0; i < a.size(); ++i) {
        for (size_t j = 0; j < b[0].size(); ++j) {
            for (size_t k = 0; k < b.size(); ++k) {
                c[i][j] = (c[i][j] + a[i][k] * b[k][j]) % mod;
            }
        }
    }

    return c;
}

一般而言，使用 vector<vector<>> 或二維陣列表示矩陣

大部分矩陣運算都要自行實作，計算方法與高中課本相同

若矩陣很大，可以預先把 b 行列互換，加速乘法效率 (快取優化) @

Prime

質數

因數

如果 $x=ab$

則 $a,b$ 是 $x$ 的因數

除了 $1$，每一個整數都有兩個顯然因數

$1,x$

因數

整除符號

如果 $a$ 是 $x$ 的因數，則使用下方法紀錄

$a\mid x$

example

$15=5\times 3$

$\therefore 3\mid 15$

$\therefore 5\mid 15$

example

不整除符號

$15\nmid 3$

$2\nmid 7$

Hint : 數字大的放後面，所以前面是因數

質數

如果一個數字 $n$ 是質數，則 $n$ 只有兩個相異的因數

$7$ 是質數，因數有 $1,7$

$6$ 不是質數，因數有 $1,2,3,6$

$1$ 不是質數，因為沒有相異的因數

$0$ 不在討論範圍

質數判定

判斷 $n$ 是不是質數

質數判定

判斷 $n$ 是不是質數

暴力方法，用 $2\sim n-1$ 的數字試試看

bool isp(int n)
{
    for(int i=2;i<n;++i)
    {
        if ( n%i==0 )
            return false;
    }
    return true;
}

時間複雜度：$O(n)$

質數判定

判斷 $n$ 是不是質數

定理 1. 若 $n=ab$, 且 $a\leq b$ 則

$a\leq \sqrt{n}$

如果 $n$ 是合數，會有一個因數小於等於 $\sqrt{n}$

可用反證法輕易得證

質數判定

判斷 $n$ 是不是質數

bool isp(int n)
{
    int s = (int) ceil(sqrt(n));
  
    for( int i=2 ; i<=s ; ++i )
    {
        if ( n%i==0 )
            return false;
    }
    return true;
}

// Way 2  
    for( int i=2 ; i*i<=n ; ++i )

注意判斷條件 <=

注意溢位 (way2)

不要把 sqrt 放到 for 上

時間複雜度：$O(\sqrt{n})$

sqrt 可能的時間複雜度為 $O(\log {n})$ @

質數判定

判斷 $x$ 是不是質數

預處理法：透過預先計算的資訊加速答案查詢

當中最有名的方法為 κόσκινον Ἐρατοσθένους

又稱為埃氏篩法 (sieve of Eratosthenes)

可以預先計算 $1\sim n$ 之間的所有數字是否為質數

質數判定

判斷 $x$ 是不是質數

埃氏篩法

先假設所有數字都是質數，0, 1 除外

vector<int> isp(n+1, true);

isp[0] = isp[1] = false;

質數判定

判斷 $x$ 是不是質數

埃氏篩法

對於一個數字 $n$，它的倍數 $2n, 3n \dots$ 一定不是質數

從 $n=2$ 開始檢查數字

vector<int> isp(n+1, true);

isp[0] = isp[1] = false;

for (int i=2;i<=n;++i)
{
    for (int j=i*2;j<=n;j+=i)
    {
        isp[j] = false;
    }
}

質數判定

判斷 $x$ 是不是質數

埃氏篩法

vector<int> isp(n+1, true);

isp[0] = isp[1] = false;

for (int i=2;i<=n;++i)
{
    for (int j=i*2;j<=n;j+=i)
    {
        isp[j] = false;
    }
}

定理. 通過此方法後，每一個合數都會被標記為 false

prof. 因為每一個合數都會被它的因數給標記

質數判定

判斷 $x$ 是不是質數

埃氏篩法

vector<int> isp(n+1, true);

isp[0] = isp[1] = false;

for (int i=2;i<=n;++i)
{
    for (int j=i*2;j<=n;j+=i)
    {
        isp[j] = false;
    }
}

時間複雜度

$n/2+n/3+n/4...n/n$

$< n(1/2+1/3+1/4+...1/n)$

$\in O(n\ln n)$

質數判定

判斷 $x$ 是不是質數

埃氏篩法

vector<int> isp(n+1, true);

isp[0] = isp[1] = false;

for (int i=2;i*i<=n;++i)
{
    for (int j=i*2;j<=n;j+=i)
    {
        isp[j] = false;
    }
}

加速 1. 外迴圈只需要到 $\sqrt{n}$

質數判定

判斷 $x$ 是不是質數

埃氏篩法

vector<int> isp(n+1, true);

isp[0] = isp[1] = false;

for (int i=2;i*i<=n;++i)
{
    for (int j=i*i;j<=n;j+=i)
    {
        isp[j] = false;
    }
}

加速 1. 外迴圈只需要到 $\sqrt{n}$

加速 2. 內迴圈只需要從 $i\times i$

質數判定

判斷 $x$ 是不是質數

埃氏篩法

vector<int> isp(n+1, true);

isp[0] = isp[1] = false;

for (int i=2;i*i<=n;++i)
{
    if (!isp[i])
        continue;
    for (int j=i*i;j<=n;j+=i)
    {
        isp[j] = false;
    }
}

加速 1. 外迴圈只需要到 $\sqrt{n}$

加速 2. 內迴圈只需要從 $i\times i$

加速 3. 不是質數不用篩

質數判定

判斷 $x$ 是不是質數

埃氏篩法

vector<int> isp(n+1, true);

isp[0] = isp[1] = false;

for (int i=2;i*i<=x;++i)
{
    if (!isp[i])
        continue;
    for (int j=i*i;j<=x;j+=i)
    {
        isp[j] = false;
    }
}

加速 1. 外迴圈只需要到 $\sqrt{x}$

加速 2. 內迴圈只需要從 $i\times i$

加速 3. 不是質數不用篩

時間複雜度

$n/2+n/3+n/5...n/p$

$< n(1/2+1/3+1/5+...1/p)$

$\in O(n\ln\ln n)$

@質數倒數和

質數判定

判斷 $x$ 是不是質數

線性篩法

如果我們能讓每一個數字只被篩掉 1 次

時間複雜度就能進一步下降

質數判定

判斷 $x$ 是不是質數

線性篩法

讓每一個數字，只被自己最小的質因數篩掉 !

$N = P_{\text{min}}\times Q$

很簡單的，可以知道 $P_{\text{min}}\leq Q$

因此可以用一個跟前面演算法類似的雙層迴圈來寫

質數判定

判斷 $x$ 是不是質數

讓每一個數字

只被自己最小的質因數篩掉 !

$N = P_{\text{min}}\times Q$

isp[0] = isp[1] = false;
for (int Q = 2; Q <= N; ++Q)
{
    if (isp[Q])
        Primes.emplace_back(Q);

    for (int P : Primes)
    {
        if (P * Q > N)
            break;
        isp[P * Q] = false;

        if (Q % P == 0) // Why ?
            break;
    }
}

第 13 行保證了上述的性質

為什麼 ?

質數判定

判斷 $x$ 是不是質數

isp[0] = isp[1] = false;
for (int Q = 2; Q <= N; ++Q)
{
    if (isp[Q])
        Primes.emplace_back(Q);

    for (int P : Primes)
    {
        if (P * Q > N)
            break;
        isp[P * Q] = false;

        if (Q % P == 0) // Why ?
            break;
    }
}

如果 $Q\%P == 0$

表示 $Q=xP$

如果我們刪除了 $N=QP'$

$P'$ 是一個大於 $P$ 的質數

那麼 $N$ 就沒有

被自己最小的質因數 $P$ 刪除

$N$ 應該要在

$Q'=xP'$ 時，被 $P$ 刪除

質數判定

判斷 $x$ 是不是質數

isp[0] = isp[1] = false;
for (int Q = 2; Q <= N; ++Q)
{
    if (isp[Q])
        Primes.emplace_back(Q);

    for (int P : Primes)
    {
        if (P * Q > N)
            break;
        isp[P * Q] = false;

        if (Q % P == 0) // Why ?
            break;
    }
}

如果 $Q\%P == 0$

表示 $Q=xP$

$N=QP'$ 應該要在

$Q'=xP'$ 時，被 $P$ 刪除

因為 $Q'>Q$

所以不會漏刪他

由於每一個數字最多只會被檢查過 $1$ 次

時間複雜度為 $O(n)$

質數判定

判斷 $n$ 是不是質數

暴力判定 $O(\sqrt{n})$

質數篩法 $O(n\ln\ln n)$

歐拉篩法 $O(n)$

質數判定

判斷 $x$ 是不是質數

唬爛方法

利用一些質數才成立的公式來檢查 $x$ 是不是質數

example

是不是奇數

是不是 $6n\pm 1$

質數判定

判斷 $x$ 是不是質數

唬爛方法

警告：質數會成立，不代表非質數就不成立！

利用一些質數才成立的公式來檢查 $x$ 是不是質數

費馬小定理

如果 $p$ 是質數，則對於正整數 $1\leq a\leq p-1$ 有

$$a^p\equiv a \pmod{p}$$

example

隨意取一個 $a$ ，則 $a^5\equiv a \mod{5}$

$2^5=32\equiv 2 \mod{5}$

$3^5=243\equiv 3 \mod{5}$

費馬小定理

如果 $p$ 是質數，則對於正整數 $1\leq a\leq p-1$ 有

$$a^p\equiv a \pmod{p}$$

Prove.

考慮 $(b+1)^p \mod{p}$

費馬小定理

如果 $p$ 是質數，則對於正整數 $1\leq a\leq p-1$ 有

$$a^p\equiv a \pmod{p}$$

Prove.

$$(b+1)^p =$$

$$\binom{p}{p}b^p+\binom{p}{p-1}b^{p-1}+\binom{p}{p-2}b^{p-2}+\binom{p}{p-3}b^{p-3}+\cdots+\binom{p}{2}b^{2}+\binom{p}{1}b^{1}+\binom{p}{0}b^{0}$$

因為 $\binom{p}{n}=\frac{p!}{n!(p-n)!}$，否則除非 $n=0,p$，分子的$ p$ 都無法被消除

所以 $\binom{p}{n}$ 會是 $p$ 的倍數

費馬小定理

如果 $p$ 是質數，則對於正整數 $1\leq a\leq p-1$ 有

$$a^p\equiv a \pmod{p}$$

Prove.

$$(b+1)^p =$$

$$\binom{p}{p}b^p+\binom{p}{p-1}b^{p-1}+\binom{p}{p-2}b^{p-2}+\binom{p}{p-3}b^{p-3}+\cdots+\binom{p}{2}b^{2}+\binom{p}{1}b^{1}+\binom{p}{0}b^{0}$$

$$\equiv \binom{p}{p}b^p+\binom{p}{0}b^{0} = b^p+1\pmod{p}$$

費馬小定理

如果 $p$ 是質數，則對於正整數 $1\leq a\leq p-1$ 有

$$a^p\equiv a \pmod{p}$$

Prove.

$$\equiv (b-1)^p+1+1\pmod{p}$$

$$\equiv (b-2)^p+1+1+1\pmod{p}$$

$$(b+1)^p \equiv b^p+1\pmod{p}$$

$$\equiv (b-3)^p+1+1+1+1\pmod{p}$$

$$\equiv\underbrace{1+1+1+1+1+1+1+1}_{b+1}\pmod{p}$$

$$\equiv b+1\pmod{p}$$

費馬小定理

如果 $p$ 是質數，則對於正整數 $1\leq a\leq p-1$ 有

$$a^p\equiv a \pmod{p}$$

Prove.

$$(b+1)^p \equiv b+1\pmod{p}$$

設 $a=b+1$ 得

$$a^p\equiv a \pmod{p} ~_\square$$

其實比較常用

$$a^{p-1}\equiv 1 \pmod{p}$$

費馬測試

如果 $p$ 是質數，則對於正整數 $1\leq a\leq p-1$ 有

$$a^p\equiv a \pmod{p}$$

隨機生成一些 $a$ 檢查有沒有滿足費馬小定理

Try ZJ a007

費馬測試

如果 $p$ 是質數，則對於正整數 $1\leq a\leq p-1$ 有

$$a^p\equiv a \pmod{p}$$

隨機生成一些 $a$ 檢查有沒有滿足費馬小定理

mt19937 mt(7122);
bool isp(ll x)
{

    ll a = mt() % (x-1) + 1;
    if( qpow( a, x ) != a ) return false;

    return true;
}

費馬測試

如果 $p$ 是質數，則對於正整數 $1\leq a\leq p-1$ 有

$$a^p\equiv a \pmod{p}$$

隨機生成一些 $a$ 檢查有沒有滿足費馬小定理

mt19937 mt(7122);
bool isp(ll x)
{

    ll a = mt() % (x-1) + 1;
    if( qpow( a, x ) != a ) return false;

    return true;
}

卡邁克爾數

一些不是質數，但是永遠滿足費馬測試的數字

$561,1105,1729,2465,2821,6601\cdots$ @

可以枚舉卡邁克爾數然後在判質數嗎？

UVA 10006

雖然這種數字很少，$1\sim n$ 之間約有 $n^{2/7}$ 個

但沒有簡單的列舉方法，long long 範圍內有 60 萬個

米勒-拉賓測試

如果 $p$ 是質數，且 $p>2$，則

1. 通過費馬測試 $a^{p-1} \equiv 1 \pmod p$

2. 對於方程式 $x^2\equiv 1 \pmod{p}$, 只有 $x=\pm 1$時成立 (方根測試)

對於第二點，帶入 $\pm 1$ 顯然成立

因此多挑一些 $x$ 同時檢驗兩件事情就好！

米勒-拉賓測試

如果 $p$ 是質數，且 $p>2$，則

1. 通過費馬測試 $a^{p-1} \equiv 1 \pmod p$

2. 對於方程式 $x^2\equiv 1 \pmod{p}$, 只有 $x=\pm 1$時成立 (方根測試)

prof.

$x^2\equiv 1$

$x^2-1 \equiv 0$

$(x-1)(x+1)\equiv 0$

米勒-拉賓測試

如果 $p$ 是質數，且 $p>2$，則

1. 通過費馬測試 $a^{p-1} \equiv 1 \pmod p$

2. 對於方程式 $x^2\equiv 1 \pmod{p}$, 只有 $x=\pm 1$時成立 (方根測試)

prof.

$x^2\equiv 1$

$x^2-1 \equiv 0$

$(x-1)(x+1)\equiv 0$

顯然的有平凡解 +1, -1

因為 $p$ 是質數

故不存在一個正整數 $1< t<p$

使得 $ p\equiv 0 \pmod t$

米勒-拉賓測試

如果 $p$ 是質數，且 $p>2$，則

1. 通過費馬測試 $a^{p-1} \equiv 1 \pmod p$

2. 對於方程式 $x^2\equiv 1 \pmod{p}$, 只有 $x=\pm 1$時成立 (方根測試)

prof.

$x^2\equiv 1$

$x^2-1 \equiv 0$

$(x-1)(x+1)\equiv 0$

顯然的有平凡解 +1, -1

所以，如果 (x-1), (x+1) 不等於 0

因為都沒有 $p$ 的因數

乘起來也不會是 $p$ 的倍數 $_\square$

米勒-拉賓測試

如果 $p$ 是質數，且 $p>2$，則

1. 通過費馬測試 $a^{p-1} \equiv 1 \pmod p$

2. 對於方程式 $x^2\equiv 1 \pmod{p}$, 只有 $x=\pm 1$時成立 (方根測試)

對於第二點，帶入 $\pm 1$ 顯然成立

因此多挑一些 $x$ 同時檢驗兩件事情就好！

米勒-拉賓測試

如果 $p$ 是質數，且 $p>2$，則

1. 通過費馬測試 $a^{p-1} \equiv 1$

2. 對於方程式 $x^2\equiv 1 \pmod{p}$, $x=\pm 1$ 是唯一的解

優化：可以在算費馬測試時，順便測試第二點！

因為 $p-1$ 是偶數，可以將 $p-1$ 分解為

$d\times 2^u$

先算 $a^d$，再平方 $u$ 次，沿途產生的數字都來測試！

Note : $u\geq 1$

以下是加速技巧

米勒-拉賓測試

如果 $p$ 是質數，且 $p>2$，則

1. 通過費馬測試 $a^{p-1} \equiv 1$

2. 對於方程式 $x^2\equiv 1 \pmod{p}$, $x=\pm 1$ 是唯一的解

因為 $p-1$ 是偶數，可以將 $p-1$ 分解為

$d\times 2^u$

計算 $a^d$

如果 $a^d \equiv \pm 1$ ，則一定通過費馬測試

則 $a^{d2^e}$一定通過方根測試

是質數

米勒-拉賓測試

如果 $p$ 是質數，且 $p>2$，則

1. 通過費馬測試 $a^{p-1} \equiv 1$

2. 對於方程式 $x^2\equiv 1 \pmod{p}$, $x=\pm 1$ 是唯一的解

因為 $p-1$ 是偶數，可以將 $p-1$ 分解為

$d\times 2^u$

計算 $a^{d2^e}$

$a^{d}\neq\pm 1, e<u$

如果 $a^{d2^e}=1$ 則不通過方根測試

因為 $x=2^{d2^{e-1}}\neq\pm1$ 卻滿足方程式

米勒-拉賓測試

如果 $p$ 是質數，且 $p>2$，則

1. 通過費馬測試 $a^{p-1} \equiv 1$

2. 對於方程式 $x^2\equiv 1 \pmod{p}$, $x=\pm 1$ 是唯一的解

因為 $p-1$ 是偶數，可以將 $p-1$ 分解為

$d\times 2^u$

計算 $a^{d2^e}$

如果 $a^{d2^e}=-1$ 則一定通過費馬測試

$a^{d2^e}$ 則一定通過方根測試

$a^{d}\neq\pm 1, e<u$

因為 $x=2^{d2^{e-1}} = -1$ ，是方程式預設的解

是質數

米勒-拉賓測試

如果 $p$ 是質數，且 $p>2$，則

1. 通過費馬測試 $a^{p-1} \equiv 1$

2. 對於方程式 $x^2\equiv 1 \pmod{p}$, $x=\pm 1$ 是唯一的解

因為 $p-1$ 是偶數，可以將 $p-1$ 分解為

$d\times 2^u$

計算 $a^{d2^u}$

如果以算到 $p-1$ 次方還沒判定是質數

就不是質數了

因為我們總是預測先預測下一步是否成立

米勒-拉賓測試

bool miller_rabin(int n, int a)
{
    if ( n==2 ) return true;
    if ( n < 2 || n % 2 == 0 ) return false;
    // 分解次方
    int u = n-1, t = 0;
    while (u % 2 == 0) u >>= 1, t++;
 
    // 先檢查 a^u
    int x = pow(a, u, n);   // x = a ^ u % n;
    if (x == 0 || x == 1 || x == n-1) return true;
 
    for (int i=0; i<t-1; i++) // 算密次剩下的部分，最後一次不用算
    {
        x = mul(x, x, n);   // x = x * x % n;
        if (x == 1) return false;  //方根測試失敗
        if (x == n-1) return true; //偷窺未來一定成功
    }
    return false; // for會偷窺歸下一步會不會成功，所以最後還沒成功就是失敗
}

米勒-拉賓測試

定理：如果 $p$ 不是質數，任選一個 $x$ 同時滿足米勒-拉賓測試的機率 $\leq 1/4$

Michael O Rabin 1980. Probabilistic algorithm for testing primality

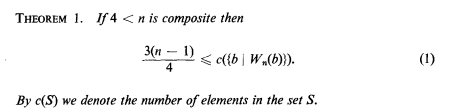
米勒-拉賓測試

如果 $p$ 是質數，且 $p>2$，則

1. 通過費馬測試

2. 對於方程式 $x^2\equiv 1 \pmod{p}$, $x=\pm 1$ 是唯一的解

定理：如果 $p$ 不是質數，任選一個 $x$ 同時滿足兩件事情的機率 $\leq 1/4$

因此，單次的正確率是 3/4

事實上，有人先找出了夠好了 $x$ 來檢驗

米勒-拉賓測試

如果 $p$ 是質數，且 $p>2$，則

1. 通過費馬測試

2. 對於方程式 $x^2\equiv 1 \pmod{p}$, $x=\pm 1$ 是唯一的解

int 範圍：選 $x=\{2,7,61\}$

long long 範圍：選 $x=$ 小於 $40$ 的所有質數

wiki = $\displaystyle 2,325,9375,28178,450775,9780504,1795265022$

GCD / LCM

最大公因數與最小公倍數

最大公因數

如果有一個數 $g$ ，同時為 $x,y$ 的因數，則 $g$ 為 $x,y$ 的公因數

$x=g\cdot a$

$y=g\cdot b$

對於任兩數，求最大的 $g$ 即為最大公因數

偷懶法

一般而言，很少直接實作 GCD
如果使用 GCC ，則 algorithm 裡面剛好有實作一個可以使用
- ```
std::__gcd(x, y)
```
如果可以使用 C++17 ，則 algorithm 有標準版的可以使用
- ```
std::gcd(x,y)
```

#include <algorithm>

// GCC Only hack
cout << std::__gcd(12, 24) << '\n';

// C++17
cout << std::gcd(12, 24) << '\n';

note : 如果 $x,y$ 其中之一為 $0$ ，則回傳另一數值

輾轉相除法

設 $x\geq y$

如果 $g$ 是 $x,y$ 的最大公因數

$x=g\cdot a$

$y=g\cdot b$

則

$g$ 也是 $x-y,y$ 的最大公因數

輾轉相除法

$x=g\cdot a$

$y=g\cdot b$

$g$ 也是 $x-y,y$ 的最大公因數

$x-y=g\cdot (a-b)$

$y=g\cdot b$

證明

我們只需要證明 $\gcd(a-b,b)$ 為 $1$

透過反證法，可得出若不為 $1$，$g$ 就不是最大公因數

輾轉相除法

$x=g\cdot a$

$y=g\cdot b$

$g$ 也是 $x-y,y$ 的最大公因數

進一步的

$g$ 也是 $x-ny,y$ 的最大公因數

$g$ 也是 $x\%y,y$ 的最大公因數

輾轉相除法

設 $x\geq y$

如果 $g$ 是 $x,y$ 的最大公因數

$g$ 也是 $y, x\% y$ 的最大公因數

int gcd(int a, int b) {
    if (b == 0)
        return a;
    return gcd(b, a%b);
}

輾轉相除法

int gcd(int a, int b) {
    if (b == 0)
        return a;
    return gcd(b, a%b);
}

時間複雜度分析

每做 1 次 $\%$ ，可以使其中一個數字的二進為長度至少減 $1$

因為總共有 $\log(a)+\log(b)$ 個 bit

複雜度為 $O(\log(a+b))$

LCM

設 $L$ 同時是 $a,b$ 的倍數，則最小的 $L$ 為最小公倍數

$x=g\cdot a$

$y=g\cdot b$

透過 $\gcd$ ，可以很簡單的構造

$L=g\cdot a \cdot b $

$=x\cdot (y/g)$

LCM

設 $L$ 同時是 $a,b$ 的倍數，則最小的 $L$ 為最小公倍數

透過 $\gcd$ ，可以很簡單的構造

$L=x\cdot (y/g)$

int lcm(int a, int b) {
    // 常見溢位陷阱
    // 不要寫成 a * b / gcd(a,b)
    // 要先除在乘
    return a * (b / gcd(a, b));
}

LCM 偷懶

C++17 以後有內建 lcm 可以直接用

#include <bits/stdc++.h>

// 沒有 __lcm!!

cout << std::lcm(6, 8) << '\n';

Factor

因數分解

因數問題

給定一個數字 $x$ ，請回答一個 $x$ 的一個不等於 $1$ 或 $x$ 的因數

可以假設 $x > 2$ 且 $x$ 不是質數

ex. 12 的因數有？

1,2,3,4,6,12

因數問題

給定一個數字 $x$ ，請回答一個 $x$ 的一個不等於 $1$ 或 $x$ 的因數

可以假設 $x > 2$ 且 $x$ 不是質數

暴力法：$O(\sqrt{x})$

ll factor(ll x)
{
    for(ll i=2;i*i<=x;++i)
    {
        if( x%i==0 ) return i;
    }
    return x; //x is prime
}

因數問題

給定一個數字 $x$ ，請回答一個 $x$ 的一個不等於 $1$ 或 $x$ 的因數

可以假設 $x > 2$ 且 $x$ 不是質數

建表法：$O( n\log\log n + \log{x})$

在做篩法的時候，幫每一個數字紀錄被誰除過

因數問題

給定一個數字 $x$ ，請回答一個 $x$ 的一個不等於 $1$ 或 $x$ 的因數

可以假設 $x > 2$ 且 $x$ 不是質數

建表法：$O( n\log\log n + \log{x})$

iota(dp, dp+n, 0);// 初始化 dp[i] = i; 
for(ll i=2;i*i<=n;++i)
{
    if( isp[i] )
    {
        for( int j=i*i; j<=n; j+=i )
        {
            isp[j] = false;
            dp[j] = i; // j 的因數有 i 
        }
    }
}

因數問題

給定一個數字 $x$ ，請回答一個 $x$ 的一個不等於 $1$ 或 $x$ 的因數

可以假設 $x > 2$ 且 $x$ 不是質數

混和大法：$O( \sqrt{n}\log\log \sqrt{n} + \pi(\sqrt{x}))$

如果數字大到建表建不下，可以至少建到$\sqrt{n}$

再用暴力法，但是只嘗試質數

練習題

d446. 生成因數 - 高中生程式解題系統 (zerojudge.tw)

Hint : 如果把一個數字質因數分解後，可以利用質因數不重複枚舉所有因數

因數問題

給定一個數字 $x$ ，請回答一個 $x$ 的一個不等於 $1$ 或 $x$ 的因數

可以假設 $x > 2$ 且 $x$ 不是質數

唬爛法

random 一個數字來猜猜看他是不是因數

因數問題

給定一個數字 $x$ ，請回答一個 $x$ 的一個不等於 $1$ 或 $x$ 的因數

可以假設 $x > 2$ 且 $x$ 不是質數

唬爛法

mt19937 mt(7122);
ll factor(ll x)
{
    int f;
    uniform_int_distribution<int> uni(2, x-1);
    do{
        f = uni(mt);
    }while( x%f!=0 );
    
    return f;
}

因數問題

給定一個數字 $x$ ，請回答一個 $x$ 的一個不等於 $1$ 或 $x$ 的因數

可以假設 $x > 2$ 且 $x$ 不是質數

唬爛法

最慘的狀況下， $x$ 只有兩個因數，故命中率為

$$\frac{2}{x-2}$$

note. 1跟x 不用嘗試

因數問題

給定一個數字 $x$ ，請回答一個 $x$ 的一個不等於 $1$ 或 $x$ 的因數

可以假設 $x > 2$ 且 $x$ 不是質數

唬爛法

如果 $x=pq$

$p,q$ 一定有一個數字小於等於 $\sqrt{x}$

所以可以縮小 random 的範圍提高機率

因數問題

給定一個數字 $x$ ，請回答一個 $x$ 的一個不等於 $1$ 或 $x$ 的因數

可以假設 $x > 2$ 且 $x$ 不是質數

唬爛法

mt19937 mt(7122);
ll factor(ll x)
{
    int f;
    uniform_int_distribution<int> uni(2, (int)sqrt(x+1));
    do{
        f = uni(mt);
    }while( x%f!=0 );
    
    return f;
}

命中率提高為

$$\frac{1}{\sqrt{x}}$$

生日攻擊

班上有 $23$ 位同學，當中有兩位同學同天生日的機率是多少？

$n$ 人選 $n^2$ 個東西，相同率為 $50\%$

$n$ 人選 $1\sim n^2$ 內的數字，相差 $\sqrt{n}$ 的機率約為 $50\%$

$n$ 人選 $1\sim n^2$ 內的數字，相同的機率約為 $50\%$

Pollard’s ρ Algorithm

給定一個數字 $x$ ，請回答一個 $x$ 的一個不等於 $1$ 或 $x$ 的因數

可以假設 $x > 2$ 且 $x$ 不是質數

透過亂數產生一個數列 $a_1,a_2,a_3,\cdots a_k$ $(1<a_i<x)$

判斷 $a_i-a_j$ 與 $x$ 的 $\gcd$ 是不是 $1$

只找 p 太浪費，連同 2p, 3p, 4p ... 一起找提高機率

至少 $\sqrt{n}$ 個選擇

如果不是就猜到了因數了

Pollard’s ρ Algorithm

給定一個數字 $x$ ，請回答一個 $x$ 的一個不等於 $1$ 或 $x$ 的因數

可以假設 $x > 2$ 且 $x$ 不是質數

有人說 $a_i = a_{i-1}^2+c \mod x$ 是一個很好的序列函數

玄學，不知道為什麼

因為這個公式會循環，要判斷循環節，如果已經循環還沒找到就失敗了 (換一個c繼續)

Pollard’s ρ Algorithm

給定一個數字 $x$ ，請回答一個 $x$ 的一個不等於 $1$ 或 $x$ 的因數

可以假設 $x > 2$ 且 $x$ 不是質數

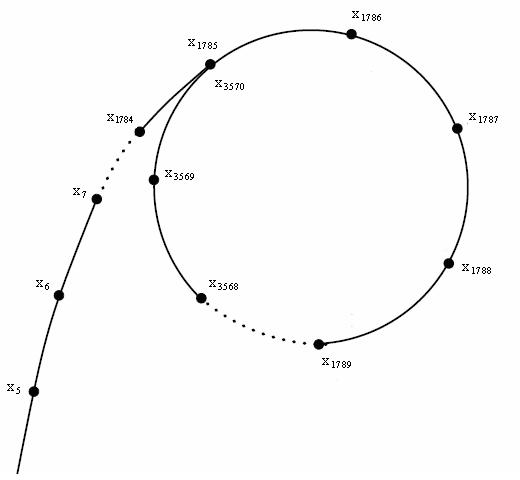
Floyd 判環法

又稱龜兔賽跑法

$x=f(x), y=f(f(y))$

讓一個兔子，一次走兩步

讓一個烏龜，一次走一步

如果出發後兔子遇到烏龜就找到循環

Brent 判環法

比前一個快一些

$x=f(x), y=x \text{ if at $2^k$ state} $

讓一個烏龜，一次走一步

讓一個兔子，在烏龜走第$2^k$ 步時，直接飛到烏龜上

其他時間睡覺不動

Pollard’s ρ Algorithm

int c, mod;
ll f(ll x)
{
    return (x*x+c)%mod;
}

ll factor(ll x)
{
    c = mt()%x;
    mod = x;
    
    ll a=2, b=2;
    
    while(true)
    {
        a = f(a);
        b = f(f(b));
        
        if( a==b ) return -1; // fail
        if( __gcd(x, abs(a-b))!=1 )
            return abs(a-b);
    }
}

Pollard’s ρ Algorithm

期望複雜度：$O(\sqrt{\sqrt{x}})=O(x^{1/4})$

因為在 $1\sim n$ 的範圍內猜 $\sqrt{n}$ 種可能

相當於在 $1\sim \sqrt{n}$ 的範圍內猜 $1$ 種可能

根據生日攻擊，只需要猜$\sqrt{\sqrt{x}}$ 次就有 $50\%$ 命中率

很唬爛的證明，但完整證明太難，從略

Pollard’s ρ Algorithm

期望複雜度：$O(\sqrt{\sqrt{x}})=O(x^{1/4})$

如果失敗就多換幾個 $c$

如果 $x$ 是質數，會進入無窮迴圈

- 用米勒-拉賓預處理

Euler's totient function

歐拉函數

歐拉函數 $\varphi(x)$ 的定義為

小於等於 $x$ 的正整數中，有多少數字與 $x$ 互質

定義 $a,b$ 互質 $\iff \gcd(a,b)=1$

$\varphi(1)=1$

$\varphi(5)=4$

$\varphi(6)=2$

$\varphi(30)=?$

$\varphi(7)=?$

$\varphi(2147483647)=?$

歐拉函數

歐拉函數 $\varphi(x)$ 的定義為

小於等於 $x$ 的正整數中，有多少數字與 $x$ 互質

性質1. 如果 $p$ 是質數，則

$\varphi(p)=p-1$

歐拉函數

歐拉函數 $\varphi(x)$ 的定義為

小於等於 $x$ 的正整數中，有多少數字與 $x$ 互質

性質2. 如果 $p$ 是質數，則

$$\varphi(p^k)=p^k-p^{k-1}=p^k(1-\frac{1}{p})$$

因為 $p$ 的倍數有 $p^k/p=p^{k-1}$ 這麼多個

歐拉函數

歐拉函數 $\varphi(x)$ 的定義為

小於等於 $x$ 的正整數中，有多少數字與 $x$ 互質

性質2. 如果 $a,b$ 互質，則

$\varphi(ab)=\varphi(a)\varphi(b)$

歐拉函數

歐拉函數 $\varphi(x)$ 的定義為

小於等於 $x$ 的正整數中，有多少數字與 $x$ 互質

性質3. 如果 $a,b$ 互質，則

$\varphi(ab)=\varphi(a)\varphi(b)$

Prove. 若 $p,q$ 是質數，則

$\varphi(pq)=pq-1-(q-1)-(p-1)$

$=pq-p-q+1$

$=(p-1)(q-1)$

$=\varphi(p)\varphi(q)$

歐拉函數

歐拉函數 $\varphi(x)$ 的定義為

小於等於 $x$ 的正整數中，有多少數字與 $x$ 互質

性質3. 如果 $a,b$ 互質，則

$\varphi(ab)=\varphi(a)\varphi(b)$

Prove. 若 $p,q$ 是質數，則同理可得

$\varphi(p^xq^y)=\varphi(p^x)\varphi(q^y)$

將 $a,b$ 質因數分解後，將全部合併即可得證

歐拉函數

歐拉函數 $\varphi(x)$ 的定義為

小於等於 $x$ 的正整數中，有多少數字與 $x$ 互質

如何計算 $\varphi(x)$

對 $x$ 做質因數分解後，用性質 2,3 暴力算

性質3. 如果 $a,b$ 互質，則

$\varphi(ab)=\varphi(a)\varphi(b)$

性質2. 如果 $p$ 是質數，則

$$\varphi(p^k)=p^k-p^{k-1}=p^k(1-\frac{1}{p})$$

快速冪！

歐拉函數

若同時需要算多個數的 $\varphi(x)$ 可以建表 !

關鍵公式

$\sum\limits_{k \mid n} \varphi(k) = n$

若 $n = 10$

$\varphi(1)+\varphi(2)+\varphi(5)+\varphi(10)$

$=1+1+4+4=10$

歐拉函數

若同時需要算多個數的 $\varphi(x)$ 可以建表 !

關鍵公式

$\sum\limits_{k \mid n} \varphi(k) = n$

若 $n = 10$

$\varphi(1)+\varphi(2)+\varphi(5)+\varphi(10)$

$=1+1+4+4=10$

$\varphi(10)=10-\varphi(1)-\varphi(2)-\varphi(5)$

$\varphi(n)=n-\sum\limits_{d\mid n, d\neq n} \varphi(d)$

歐拉函數

證明

$\sum\limits_{k \mid n} \varphi(k) = n$

設 $f(x)$ 為有多少 $k$ 使 $\gcd(k,n)=x$

$1\leq k \leq n$

根據定義 $\sum\limits_{i=1}^n f(i) = n$

$1$ 個 $k$ 只會出現在某一個 $f$ 中

$\gcd(k,n)=x \Rightarrow \gcd\left(\frac{k}{x}, \frac{n}{x}\right)=1$

設 $f(x)$ 為有多少 $k$ 使 $\gcd(k,n)=x$

歐拉函數

證明

$\sum\limits_{k \mid n} \varphi(k) = n$

設 $f(x)$ 為有多少 $k$ 使 $\gcd(k,n)=x$

$1\leq k \leq n$

根據定義 $\sum\limits_{i=1}^n f(i) = n$

$1$ 個 $k$ 只會出現在某一個 $f$ 中

$\gcd(k,n)=x \Rightarrow \gcd\left(\frac{k}{x}, \frac{n}{x}\right)=1$

設 $f(x)$ 為有多少 $k$ 使 $\gcd\left(\frac{k}{x}, \frac{n}{x}\right)=1$

$f(x) = \varphi(\frac{n}{x})$

歐拉函數

證明

$\sum\limits_{k \mid n} \varphi(k) = n$

設 $f(x)$ 為有多少 $k$ 使 $\gcd(k,n)=x$

$1\leq k \leq n$

根據定義 $\sum\limits_{i=1}^n f(i) = n$

$f(x) = \varphi(\frac{n}{x})$

$\sum\limits_{x\mid n}\varphi(\frac{n}{x}) = n$

$x$ 是 $n$ 所有的因數

$n/x$ 也是 $n$ 所有的因數

歐拉函數

證明

$\sum\limits_{k \mid n} \varphi(k) = n$

設 $f(x)$ 為有多少 $k$ 使 $\gcd(k,n)=x$

$1\leq k \leq n$

根據定義 $\sum\limits_{i=1}^n f(i) = n$

$f(x) = \varphi(\frac{n}{x})$

$\sum\limits_{x\mid n}\varphi(\frac{n}{x}) =\sum\limits_{x\mid n}\varphi(x) = n$

$x$ 是 $n$ 所有的因數

$n/x$ 也是 $n$ 所有的因數

歐拉函數

歐拉函數 $\varphi(x)$ 的定義為

小於等於 $x$ 的正整數中，有多少數字與 $x$ 互質

如何計算 $\varphi(x)$

找自己的因數很麻煩

但是找自己的倍數很簡單

把自己的倍數都扣掉自己的 $\varphi(x)$

歐拉函數

歐拉函數 $\varphi(x)$ 的定義為

小於等於 $x$ 的正整數中，有多少數字與 $x$ 互質

如何計算 $\varphi(x)$

void phiTable(){
	for(int i=1;i<=N;i++)
            phi[i]=i;

	for(int i=1;i<=N;i++)    //對於每一個數由小到大
            for(x=i*2;x<=N;x+=i) // 每一個倍數
                phi[x]-=phi[i];  // 都扣掉自己的 phi
}

$O(n\log n) 打表$

歐拉函數

歐拉函數 $\varphi(x)$ 的定義為

小於等於 $x$ 的正整數中，有多少數字與 $x$ 互質

小練習

https://toj.tfcis.org/oj/pro/427/

應該10~20行可ac !?

歐拉定理

如果 $a,n$ 互質，則

$$a^{\varphi(n)}\equiv 1 \pmod{n}$$

當 $n$ 是質數時就是費馬小定理

$$a^{p-1}\equiv 1 \pmod{p}$$

歐拉定理

如果 $a,n$ 互質，則

$$a^{\varphi(n)}\equiv 1 \pmod{n}$$

Prove：假設1~n之間與 n 互質的數字是

$\{x_1, x_2,x_3,\dots, x_{\varphi(n)}\}$

1. 這集合有所有與 n 互質的數字

2. 這集合任兩數字都不一樣

歐拉定理

如果 $a,n$ 互質，則

$$a^{\varphi(n)}\equiv 1 \pmod{n}$$

同乘 $a$

$\{ax_1, ax_2,ax_3,\dots, ax_{\varphi(n)}\}$

Prove：假設1~n之間與 n 互質的數字是

$\{x_1, x_2,x_3,\dots, x_{\varphi(n)}\}$

歐拉定理

如果 $a,n$ 互質，則

$$a^{\varphi(n)}\equiv 1 \pmod{n}$$

1. 這集合有所有與 n 互質的數字

2. 這集合任兩數字都不一樣

Prove：假設1~n之間與 n 互質的數字是

$\{x_1, x_2,x_3,\dots, x_{\varphi(n)}\}$

$\{ax_1, ax_2,ax_3,\dots, ax_{\varphi(n)}\}$

所以把新的序列 $\mod n$ 會是舊序列重新排列組合的一種

歐拉定理

如果 $a,n$ 互質，則

$$a^{\varphi(n)}\equiv 1 \pmod{n}$$

Prove：假設1~n之間與 n 互質的數字是

$\{x_1, x_2,x_3,\dots, x_{\varphi(n)}\}$

$\{ax_1, ax_2,ax_3,\dots, ax_{\varphi(n)}\}$

$$\prod_{\varphi(n)}{x_i}\equiv\prod_{\varphi(n)}{ax_i}\equiv a^{\varphi(n)}\prod_{\varphi(n)}{x_i} \mod n$$

歐拉定理

如果 $a,n$ 互質，則

$$a^{\varphi(n)}\equiv 1 \pmod{n}$$

Prove：同除 $\prod_{\varphi(n)}{x_i}$

$$\prod_{\varphi(n)}{x_i}\equiv\prod_{\varphi(n)}{ax_i}\equiv a^{\varphi(n)}\prod_{\varphi(n)}{x_i} \mod n$$

$$1\equiv a^{\varphi(n)} \mod n ~$$

Hint : 因為與 $n$ 互質

模除法運算

在一般題目中，如果數字過大，經常需要取模輸出
取模在加減乘上都是很簡單的
- $(a+b) \% m\equiv a\%m+b\%m$
- $(a-b) \% m\equiv a\%m-b\%m$
- $(a\times b) \% m\equiv a\%m\times b\%m$
但無法直接做除法 !

注意在 C++ 負數取模是負數 !

cout << -5 % 2 << '\n'; // -1

cout << ((a-b)%m + m)%m << '\n'; // 確保結果是正數或 0

模除法運算

$a = cx, b=x$

計算 $a/b \mod p$

相當於找一個 $x^{-1}$ ，滿足 $xx^{-1}=1$

$a/b = a \times x^{-1} = cxx^{-1} = c \mod p$

我們稱 $x^{-1}$ 為 $x$ 的模反元素

模除法運算

$a = cx, b=x$

計算 $a/b \mod p$

相當於找一個 $x^{-1}$ ，滿足 $xx^{-1}=1$

我們稱 $x^{-1}$ 為 $x$ 的模反元素

如果 $p$ 是質數，根據歐拉定理

$x^{\varphi(p)}=x^{p-1}\equiv 1 \mod p$

$x\cdot x^{p-2}\equiv 1 \mod p$

除以 $x$ 等於乘上 $x^{p-2}$

模反元素

根據歐拉定理，可以得到一般性的模除法方法 !

如果 $x, n$ 互質，根據歐拉定理

$x^{\varphi(n)}\equiv 1 \mod n$

$x\cdot x^{\varphi(n) -1}\equiv 1 \mod p$

補充 : 也可以使用 廣義輾轉相除法 解下方程式的整數解

$xx^{-1}+nb=1$

該方程式有解的條件一樣是 $x,n$ 互質

歐拉降冪法

如果 $a,n$ 互質，則

$$a^{\varphi(n)}\equiv 1 \pmod{n}$$

如果 $a,n$ 互質，冪次結果會每 $\varphi(n)$ 循環一輪

如果 $a,n$ 不互質呢？

$$a^k=a^{k\%\varphi(n)} \pmod{n}$$

其實還是會每 $\varphi(n)$ 循環一輪，但第一輪可能不在循環節內

歐拉降冪法

對於任意的 $a,n$，降冪公式如下

$$a^k\equiv{\begin{cases}a^k & k<\varphi(n) \\a^{k\%\varphi(n)+\varphi(n)} & k\geq \varphi(n)\end{cases}}$$

證明太長，自行 Google

歐拉降冪法

對於任意的 $a,n$，降冪公式如下

有了降冪法，可以保證指數的部分最多只會是 $2n$

可以避免一些題目的大數 (雖然應該是要考降冪法)

$$a^k\equiv{\begin{cases}a^k & k<\varphi(n) \\a^{k\%\varphi(n)+\varphi(n)} & k\geq \varphi(n)\end{cases}}$$

歐拉降冪法

高冪次的求解

$$a^{b^{c^d}}\equiv a^{b^{c^d}\%\varphi(n)+\varphi(n)} \mod n$$

遞迴求

$$b^{c^d} \mod \varphi(n)$$

要小心 $b^{c^d} < \varphi(n)$ 時不能加 $\varphi(n)$ 有機會壞掉

歐拉降冪法

https://toj.tfcis.org/oj/pro/179/

UVA 10692

要小心 $b^{c^d} < \varphi(n)$ 時不能加 $\varphi(n)$ 有機會壞掉

很多測資沒測這點 (或正解根本寫錯)，自己小心

Multiplication

大數乘法

大數運算

如果一個數字 $n$ 的大小超過了硬體限制的範圍，就無法直接當作一個單位運算
此時只能透過軟體模擬，讓以往可以忽視複雜度的部份不再可以忽略

long long a, b;
cin >> a >> b;
cout << a * b << '\n';

簡易大數

using BigNum = vector<int>;
BigNum& trim(BigNum &b) {
    while(b.size() > 1 && b.back() == 0)
        b.pop_back();
    return b;
}

BigNum stob(const string &s) {
    BigNum b;
    for(char c:s | views::reverse) // C++20
    	b.emplace_back(c - '0');
    return trim(b);
}

void show(const BigNum &b) {
    for(auto i : b | views::reverse) cout << i;
    cout << '\n';
}

只考慮正整數

views::reverse

反向遍歷

#include<ranges>

vector<int> a {1,2,3,4,5};

//old C++ : 1 2 3 4 5
for(vector<int>::iterator it=a.begin(), e=a.end();it!=e;++it)
	cout << *it << ' ';
    
//old C++ : 5 4 3 2 1 
for(vector<int>::reverse_iterator it=a.rbegin(), e=a.rend();it!=e;++it)
	cout << *it << ' ';

// C++11 1 2 3 4 5
for(int i:a) cout << i << ' ';

// C++20 5 4 3 2 1
for(int i:a | views::reverse) cout << i << ' ';

樸素大數乘法

模擬直式乘法

   1 2 
x  3 4
-------
   4 8
 3 6
-------    (結果相加)
 3 10 8
-------    (處理進位)
 4 0 8

樸素大數乘法

BigNum& advance(BigNum& b) {
    for(int i=0;i+1<b.size();++i){
        b[i+1] += b[i]/10;
        b[i]%=10;
    }
    return b;
}

BigNum mul(const BigNum &a, const BigNum &b)
{
    BigNum c(a.size() + b.size());
    for(int i=0;i<a.size();++i)
        for(int j=0;j<b.size();++j)
            c[i+j] += a[i] * b[j];
    
    return trim(advance(c));
}

很明顯 $O(n^2)$

Karatsuba algorithm

Karatsuba 是第一個比樸素乘法還要快的演算法

把數字分解成數段，分別乘起來後再組合

$x = x_1B^m+x_2$

$y = y_1B^m+y_2$

Karatsuba algorithm

$x = x_1B^m+x_2$

$y = y_1B^m+y_2$

$xy=x_1y_1B^{2m}+(x_1y_2+x_2y_1)B^m+x_2y_2$

由於 $x_1,x_2,y_1,y_2$ 是原來 $x,y$ 長度的一半

經過變換後變成做 4 個比較小的乘法

Karatsuba algorithm

$xy=x_1y_1B^{2m}+(x_1y_2+x_2y_1)B^m+x_2y_2$

由於 $x_1,x_2,y_1,y_2$ 是原來 $x,y$ 長度的一半

經過變換後變成做 4 個比較小的乘法

複雜度 $T(n)=4T(\frac{n}{2})+O(n)$

根據主定理 $O(T(n))\in O(n^{\log_2 4})=O(n^2)$

一點也沒變好 !?

Karatsuba algorithm

$xy=x_1y_1B^{2m}+(x_1y_2+x_2y_1)B^m+x_2y_2$

$x_1y_2+x_2y_1 =$

$(x_1+x_2)(y_1+y_2)-x_1y_1-x_2y_2$

其中 $x_1y_1,x_2y_2$ 已經算過了 !

只需要再算 $(x_1+x_2)(y_1+y_2)$

Karatsuba algorithm

$xy=x_1y_1B^{2m}+(x_1y_2+x_2y_1)B^m+x_2y_2$

$x_1y_2+x_2y_1 =$

$(x_1+x_2)(y_1+y_2)-x_1y_1-x_2y_2$

把一個乘法變成很多加減法

複雜度 $T(n)=3T(\frac{n}{2})+O(n)$

根據主定理 $O(T(n))\in O(n^{\log_2 3})=O(n^{1.5826})$

賺!

Karatsuba algorithm

$xy=x_1y_1B^{2m}+(x_1y_2+x_2y_1)B^m+x_2y_2$

$x_1y_2+x_2y_1 =$

$(x_1+x_2)(y_1+y_2)-x_1y_1-x_2y_2$

把一個乘法變成很多加減法

複雜度 $T(n)=3T(\frac{n}{2})+O(n)$

根據主定理 $O(T(n))\in O(n^{\log_2 3})=O(n^{1.5826})$

賺!

Karatsuba algorithm

除了本次課程的拆解方法，後續的研究有提出更快更噁心的拆法，多用於科學計算上

Example :

Toom-Cook Algorithm $O(n^{1.46})$

這東西用 C/C++ 實做有點長度，參見卦長模板

不過我們還要更快!

Cooley–Tukey FFT algorithm

$O(n\log n\log\log n)$

回到回到樸素大數乘法

$C=AB$

處理進位問題之前， C 的第 x 位數的值為

$C_x=A_0B_x+A_1B_{x-1}+A_2B_{x-2}\cdots+A_xB_0$

c[i+j] += a[i] * b[j];

把數字轉換成一個多項式，那大數相乘的結果與多項式相乘是類似的!

如果 $A = 789$，設 $f_A(x)=7x^2+8x+9$

如果 $B = 345$，設 $f_B(x)=3x^2+4x+5$

那 $f_A(x)f_B(x)=f_C(x)=c_0+c_1x+c_2x^2+\cdots$

其中 $c_i=a_0b_i+a_1b_{i-1}+a_2b_{i-2}+\cdots+a_ib_0$

與前頁 $C_x=A_0B_x+A_1B_{x-1}+A_2B_{x-2}\cdots+A_xB_0$ 一樣!

捲積

定義大小為 $n$ 的離散卷積($*$)如下

$f(x), g(x)$ 為函數

則 $f*g=\sum\limits^{n}_{i=0} f(i)g(n-i)$

也就是做大數乘法的動作，等於對每一個系數求卷積

單純名詞介紹，但記住這個定義可以把這演算法推廣到不僅是乘法上，只要長得像卷積就可以

即便把問題變成求多項式相乘的係數好像也沒什麼用
但是如果把多項式變成更有趣的形式有沒有幫助呢 ?

插值多項式唯一性定理

給定 $n+1$ 個點 $(x_1,y_1), (x_2, y_2),\cdots (x_{n+1}, y_{n+1})$

當中 $x$ 皆不相等

則存在唯一的 $n$ 次多項式經過這些點

by 高中數學 : 牛頓法 / 拉格朗日插值

希望你還沒還給你的老師

插值多項式唯一性定理

設 $ f(x) = 3x^2+5x+7$

任取三個點

$f(1)=15$

$f(2)=24$

$f(3)=49$

拉格朗日插值

$f(x)=$

$15\times \frac{(x-2)(x-3)}{(1-2)(1-3)}+\\24\times \frac{(x-1)(x-3)}{(2-1)(2-3)}+\\49\times\frac{(x-1)(x-2)}{(3-1)(3-2)}=\\3x^2+5x+7$

插值多項式唯一性定理

$ f(x) = 3x^2+5x+7$

$f(1)=15$

$f(2)=24$

$f(3)=49$

插值法

取樣

再談多項式乘法

$f_C(x)=f_A(x)f_B(x)$

如果 $A,B$ 都是 $n$ 次多項式，那 $C$ 就是 $2n$ 次多項式

透過 $f_A$ , $f_B$ 採樣 $f_C$ 的 $2n+1 個點$

利用插值法拼回 $f_C$ 的樣子

就能避免樸素多項式乘法了!

那怎麼做取樣 / 差值 ?

離散傅立葉變換

$ f(x) = 3x^2+5x+7$

$f(\omega)=a$

$f(\omega^2)=b$

$f(\omega^3)=c$

逆離散傅立葉變換

離散傅立葉變換

選擇 "夠好的點" 採樣，讓採樣插值都很快!

夠好的點 - 單位根 $\omega$

$n$ 次單位根是 $x^n=1$ 的所有複數 (有 $i$ 的那個) 解
高中數學範圍內教過 3 次原根

$$1, \frac{1+\sqrt{3}i}{2},\frac{1-\sqrt{3}i}{2} $$

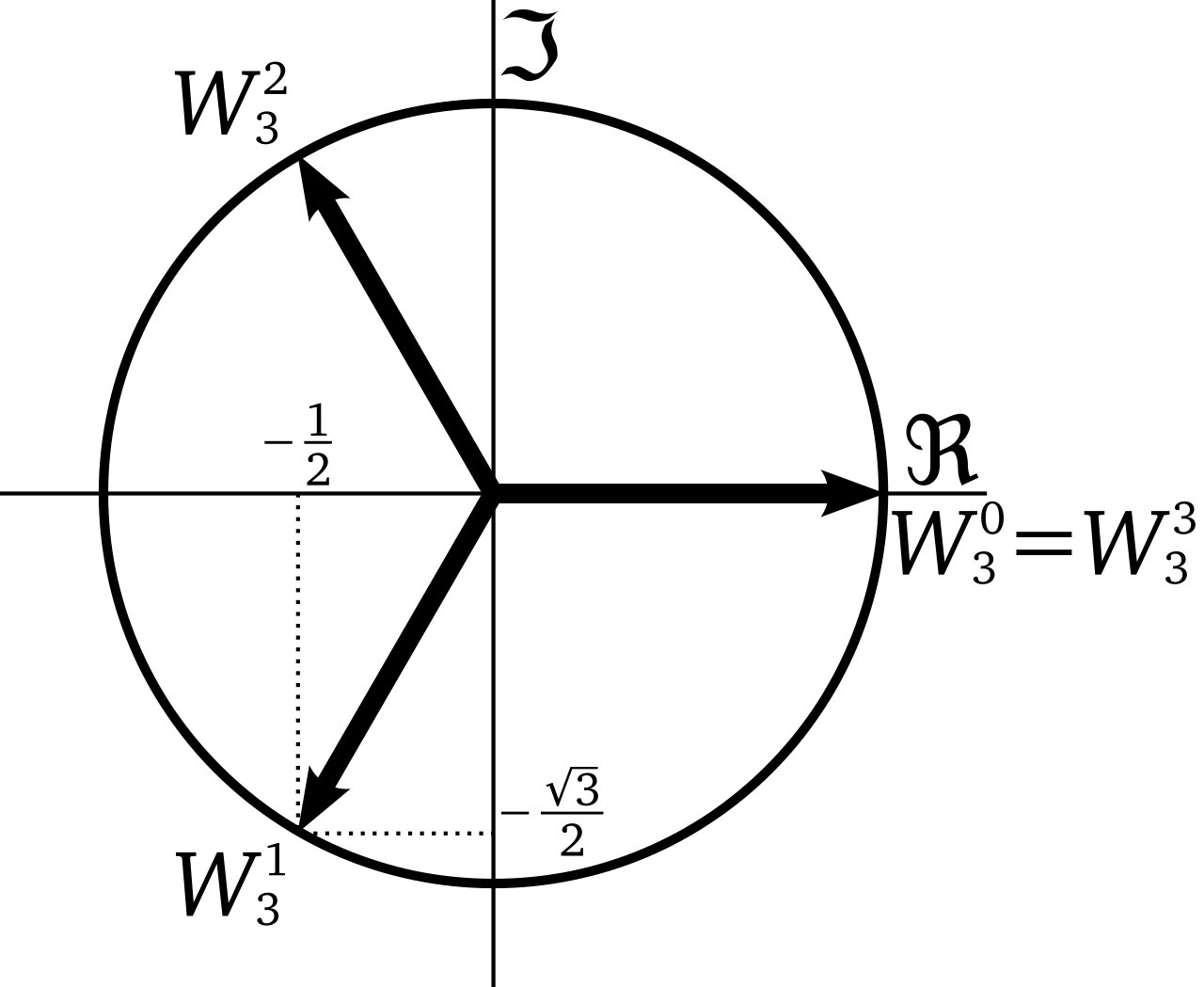
單位根 $\omega$

$n$ 次單位根剛好可以表示為

在複數平面上的一個正 $n$ 邊形，

頂點都在半徑為 1
原點在 $0+0i$ 上的圓

其中一個頂點在 $1+0i$

單位根 $\omega$

$n$ 次單位根剛好可以表示為

在複數平面上的一個正 $n$ 邊形，

頂點都在半徑為 1
原點在 $0+0i$ 上的圓

其中一個頂點在 $1+0i$

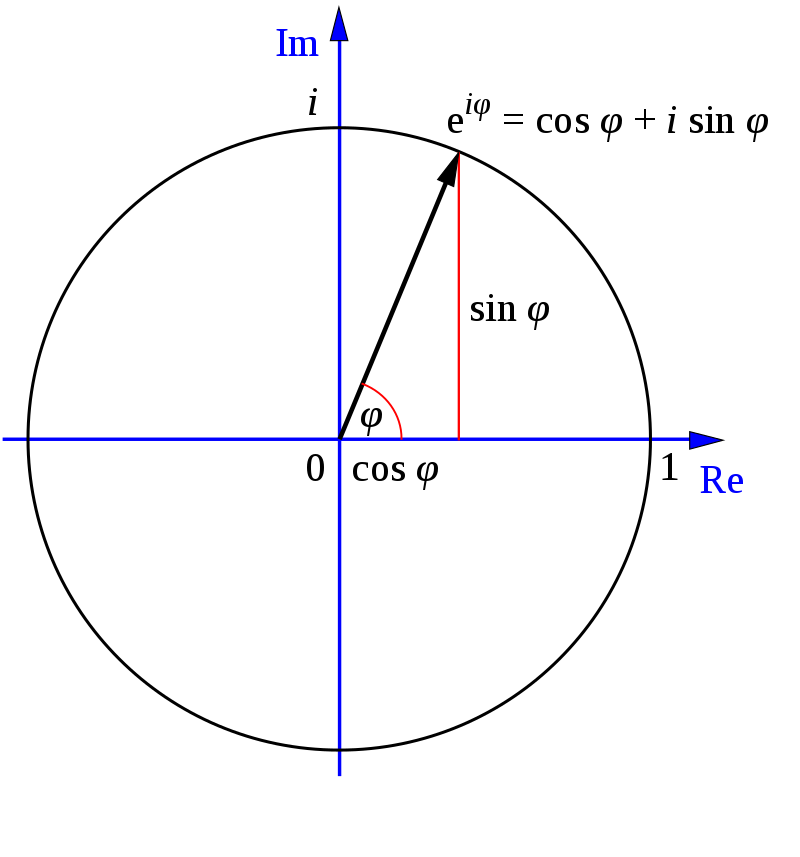
利用圖形的關係，來得到單位根的數值 !

$\omega = \exp(\frac{2\pi}{n}i)=\cos{\frac{2\pi}{n}}+i\sin\frac{2\pi}{n}$

離散傅立葉變換

對一個 $n-1$ 次多項式 $f(x)=a_0+a_1x^1+\cdots+a_{n-1}x^{n-1}$，

求 $f(1), f(\omega), f(\omega^2), f(\omega^3)\cdots ,f(\omega^{n-1})$

其中 $\omega$ 是 $n$ 次原根

{\begin{bmatrix} 1&1&1&1&\cdots &1\\ 1&\omega &\omega ^{2}&\omega ^{3}&\cdots &\omega ^{N-1}\\ 1&\omega ^{2}&\omega ^{4}&\omega ^{6}&\cdots &\omega ^{2(N-1)}\\ 1&\omega ^{3}&\omega ^{6}&\omega ^{9}&\cdots &\omega ^{3(N-1)}\\ \vdots &\vdots &\vdots &\vdots &\ddots &\vdots \\ 1&\omega ^{N-1}&\omega ^{2(N-1)}&\omega ^{3(N-1)}&\cdots &\omega ^{(N-1)(N-1)} \end{bmatrix}} {\begin{bmatrix} a_0 \\ a_1 \\ a_2 \\ \vdots \\ a_{n-1} \end{bmatrix}}= {\begin{bmatrix} f(1) \\ f(\omega^1) \\ f(\omega^2) \\ \vdots \\ f(\omega^{n-1}) \end{bmatrix}}

對一個 $n-1$ 次多項式 $f(x)=a_0+a_1x^1+\cdots+a_{n-1}x^{n-1}$，

求 $f(1),f(\omega), f(\omega^2), f(\omega^3)\cdots,f(\omega^{n-1})$

利用矩陣表示前面的運算

逆離散傅立葉變換

由 $f(1), f(\omega^1), f(\omega^2)\cdots ,f(\omega^{n-1})$ 求出

一個 $n-1$ 次多項式 $f(x)=a_0+a_1x^1+\cdots+a_{n-1}x^{n-1}$
的所有係數

基本上什麼詭異差值法都很麻煩
可以利用前一頁的式子
把這個問題變成乘上那一大團東西的反矩陣

所以這一團東西的反矩陣是 ???

\frac{1}{N}

-1

證明：乘起來會變單位矩陣...

那東西的反矩陣是 ...

using CBigNum = vector<complex<double>>;
CBigNum btoc(const BigNum &b, int N) {
    CBigNum c;
    for(auto i:b) c.emplace_back(i);
    while(c.size() < N) c.emplace_back(0);
    return c;
}

BigNum ctob(const CBigNum &c) {
    BigNum b;
    for(auto i:c) b.emplace_back(round(i.real()));
    return b;
}

使用該方法有小數精確度問題，要小心

BigNum mul2(const BigNum &a_, const BigNum &b_)
{
    int N = a_.size() + b_.size();

    CBigNum a = btoc(a_, N);
    CBigNum b = btoc(b_, N);

    auto fft = [=](const CBigNum &a, bool inv)-> CBigNum {
		/*next page*/
    };

    a = fft(a, false);
    b = fft(b, false);

    for(int i=0;i<N;++i)
        a[i] *= b[i];

    a = fft(a, true);
    auto res = ctob(a);
    return trim(advance(res));
}

auto fft = [=](const CBigNum &a, bool inv)-> CBigNum {
    //C++20, or PI = acos(-1)
    constexpr double PI = std::numbers::pi; 
    constexpr auto I = complex<double>(0, 1);

    int flag = inv ? -1 : 1;

    CBigNum res(a.size());
    for(int i=0;i<N;++i)
        for(int j=0;j<N;++j)
            res[i] += a[j] * exp( flag* i*j*(2*PI/N) * I);

    if (inv) for(auto &c:res) c/=N;

    return res;
};

就按照前面公式乘一乘，加一加

離散傅立葉變換

基本上來說，離散傅立葉/逆離散傅立葉變換幾乎一模一樣
矩陣乘法複雜度 $ O(n\times n \times 1) = O(n^2)$

完全沒有變好!!

但是這個矩陣夠怪，應該有可以加速的地方

快速傅立葉變換 FFT

在 $O(n\log n)$ 的時間乘上那一個奇怪的矩陣

快速傅立葉變換 FFT

假設 $f(x)$ 有 $2n$ 項
考慮 $f(w^x)=a_0+a_1\omega^x+a_2\omega^{2x}+\cdots+a_{2n-1}\omega^{(2n-1)x}$

把奇偶項分開

$f(w^x)=a_0+a_2\omega^{2x}+a_4\omega^{4x}+\cdots+a_{2n-2}\omega^{(2n-2)x}+$

$a_1\omega^{x}+a_3\omega^{3x}+a_5\omega^{5x}+\cdots+a_{2n-1}\omega^{(2n-1)x}$

$\omega^{x}(a_1+a_3\omega^{2x}+a_5\omega^{4x}+\cdots+a_{2n-1}\omega^{(2n-2)x})$

這個 $\omega$ 是 $2n$ 次原根

快速傅立葉變換 FFT

$f(w^x)=a_0+a_2\omega^{2x}+a_4\omega^{4x}+\cdots+a_{2n-2}\omega^{(2n-2)x}+$

$\omega^{x}(a_1+a_3\omega^{2x}+a_5\omega^{4x}+\cdots+a_{2n-1}\omega^{(2n-2)x})$

單位根的性質 1

2n 次單位根的偶數次方 $\omega^0, \omega^2, \omega^4...$

恰等於 n 次單位根的所有組合

快速傅立葉變換 FFT

$f(w^x)=a_0+a_2\omega^{2x}+a_4\omega^{4x}+\cdots+a_{2n-2}\omega^{(2n-2)x}+$

$\omega^{x}(a_1+a_3\omega^{2x}+a_5\omega^{4x}+\cdots+a_{2n-1}\omega^{(2n-2)x})$

單位根的性質 1

2n 次單位根的偶數次方 $\omega^0, \omega^2, \omega^4...$

恰等於 n 次單位根的所有組合

因此預先遞迴計算

$f_{even}(x)=a_0+a_2x+a_4x^2+a_{2n-2}{x^{n-1}}$ 的傅立葉變換

$f(1), f(\omega_{n}^1), f(\omega_{n}^2)\cdots f(\omega_{n}^{n-1})$

就能使用其結果組合答案 !

快速傅立葉變換 FFT

$f(w^x)=a_0+a_2\omega^{2x}+a_4\omega^{4x}+\cdots+a_{2n-2}\omega^{(2n-2)x}+$

$\omega^{x}(a_1+a_3\omega^{2x}+a_5\omega^{4x}+\cdots+a_{2n-1}\omega^{(2n-2)x})$

預先遞迴計算

$f_{even}(x)=a_0+a_2x+a_4x^2+a_{2n-2}{x^{n-1}}$ 的傅立葉變換 $f_{even}(\omega_n^x)$

$f_{odd}(x)=a_1+a_3x+a_5x^2+a_{2n-1}{x^{n-1}}$ 的傅立葉變換 $f_{odd}(\omega_n^x)$

那 $f(\omega_{2n}^x)=$

$f_{even}(w_{2n}^{2x})+\omega_{2n}^xf_{odd}(w_{2n}^{2x})$

$=f_{even}(w_{n}^x)+\omega_{2n}^xf_{odd}(w_{n}^x)$

對於所有 $x < n$ 成立

快速傅立葉變換 FFT

$f(w^x)=a_0+a_2\omega^{2x}+a_4\omega^{4x}+\cdots+a_{2n-2}\omega^{(2n-2)x}+$

$\omega^{x}(a_1+a_3\omega^{2x}+a_5\omega^{4x}+\cdots+a_{2n-1}\omega^{(2n-2)x})$

$f(\omega_{2n}^x)=f_{even}(w_{n}^x)+\omega_{2n}^xf_{odd}(w_{n}^x)$

對於所有 $x < n$ 成立

$f(\omega_{2n}^{x+n})=f_{even}(w_{2n}^{2(x+n)})+\omega_{2n}^{x+n}f_{odd}(w_{2n}^{2(x+n)})$

$=f_{even}(w_{n}^{x+n})+\omega_{2n}^{x+n}f_{odd}(w_{n}^{x+n})$

根據單位根的定義，$n$ 次單位根 $\omega_n$ 是 $x^n=1$ 的解 $(\omega_n^n=1)$

$=f_{even}(w_{n}^{x}\times 1)+\omega_{2n}^{x+n}f_{odd}(w_{n}^{x}\times 1)$

快速傅立葉變換 FFT

$f(w^x)=a_0+a_2\omega^{2x}+a_4\omega^{4x}+\cdots+a_{2n-2}\omega^{(2n-2)x}+$

$\omega^{x}(a_1+a_3\omega^{2x}+a_5\omega^{4x}+\cdots+a_{2n-1}\omega^{(2n-2)x})$

$f(\omega_{2n}^x)=f_{even}(w_{n}^x)+\omega_{2n}^xf_{odd}(w_{n}^x)$

對於所有 $x < n$ 成立

$f(\omega_{2n}^{x+n})=f_{even}(w_{n}^{x})+\omega_{2n}^{x+n}f_{odd}(w_{n}^{x})$

進一步的 $\omega^n_{2n}=\omega_{2}=-1$

$=f_{even}(w_{n}^{x})-\omega_{2n}^{x}f_{odd}(w_{n}^{x})$

快速傅立葉變換 FFT

$f(w^x)=a_0+a_2\omega^{2x}+a_4\omega^{4x}+\cdots+a_{2n-2}\omega^{(2n-2)x}+$

$\omega^{x}(a_1+a_3\omega^{2x}+a_5\omega^{4x}+\cdots+a_{2n-1}\omega^{(2n-2)x})$

$f(\omega_{2n}^x)=f_{even}(w_{n}^x)+\omega_{2n}^xf_{odd}(w_{n}^x)$

對於所有 $x < n$ 成立

$f(\omega_{2n}^{x+n})=f_{even}(w_{n}^{x})-\omega_{2n}^{x}f_{odd}(w_{n}^{x})$

於是所有的 $f(\omega^x)$ 就都能用 $f_{even}, f_{odd}$ 表示出來了!

如果令輸入長度是 $n=2^t$ ，就能完美的不斷遞迴此公式 !

BigNum mul3(const BigNum &a_, const BigNum &b_)
{
    int N = a_.size() + b_.size();
    int p2 = 1;
    while (p2 < N) p2*=2; 
    N = p2; // 要把 N 補成 2 的次方

    CBigNum a = btoc(a_, N);
    CBigNum b = btoc(b_, N);

	//... 下面跟前面一樣， fft_r 下頁解說
    a = fft_r(a, false, N);
    b = fft_r(b, false, N);
    //...
}

CBigNum fft_r(const CBigNum &a, bool inv, int N, bool first = true) {
    constexpr double PI = std::numbers::pi; //C++20, or acos(-1)
    constexpr auto I = complex<double>(0, 1);
    int flag = inv ? -1 : 1;

    CBigNum res(a);
    if (N==1) 
        return a;

    CBigNum even, odd;
    for(int i=0;i<N;++i) {
        if (i % 2 == 0) even.emplace_back(a[i]);
        else odd.emplace_back(a[i]);
    }

    even = fft_r(even, inv, N/2, false);
    odd  = fft_r(odd , inv, N/2, false);

    for(int i=0;i<N/2;++i) {
        res[i]     = even[i] + odd[i] * exp( flag * i * (2*PI/N) * I);
        res[i+N/2] = even[i] - odd[i] * exp( flag * i * (2*PI/N) * I);
    }

    if (inv&&first) for(auto &c:res) c/=N;
    return res;
}

快速傅立葉變換

快速傅立葉變換每次將輸入分解成大小為一半的兩個子問題
花費時間 $T(n)=2T(n/2)+O(n)$
根據主定理，$O(T(n)=O(n\log n)$

於是我們可以在 $O(n\log n)$的時間來處理大數乘法了!

不過常數有點大 !?

快速傅立葉變換 - 迴圈版

透過分析遞迴的過程，來把遞迴的程式改寫成迴圈的
當中關鍵點在 "奇偶分割" 的步驟

for(int i=0;i<N;++i) {
    if (i % 2 == 0) even.emplace_back(a[i]);
    else odd.emplace_back(a[i]);
}

快速傅立葉變換 - 迴圈版

我們可以重複使用陣列來擺放資料，讓要處理的資料連續就好

0	1	2	3	4	5	6	7

n = 8

n = 4

n = 2

0	4	2	6	1	5	3	7

n = 1

0	4	2	6	1	5	3	7

0	2	4	6	1	3	5	7

快速傅立葉變換 - 迴圈版

0	1	2	3	4	5	6	7

n = 8

0	4	2	6	1	5	3	7

n = 1

要用迴圈的話，要從 n=1 開始計算

問題是 n = 1 的那一層資料是怎麼放的 ?

方法 1. 模擬交換一遍 $O(n\log n)$

方法 2. 根據觀察
把第 $x$ 個資料放在第 $\operatorname{bit\_reverse}(x)$ 個格子上面

bit_reverse

把一個長度為 N 的數字二進位前後顛倒
像是 110010 變成 010011
C++ 沒有內建這東西，不難寫，看想寫得多花式...

unsigned int bit_rev_simple(unsigned int a, int N) {
    unsigned int ans = 0;
    for(int i=0;i<N;++i) {
        ans = ans*2 + a%2;
        a/=2;
    }
    return ans;
}
unsigned int bit_rev(unsigned int a,int N) {
    a=((a&0x55555555U)<<1)|((a&0xAAAAAAAAU)>>1);
    a=((a&0x33333333U)<<2)|((a&0xCCCCCCCCU)>>2);
    a=((a&0x0F0F0F0FU)<<4)|((a&0xF0F0F0F0U)>>4);
    a=((a&0x00FF00FFU)<<8)|((a&0xFF00FF00U)>>8);
    a=((a&0x0000FFFFU)<<16)|((a&0xFFFF0000U)>>16);
    return a>>(32-N);
}

CBigNum fft(const CBigNum &a, bool inv, int N) {
    constexpr double PI = std::numbers::pi;
    constexpr auto I = complex<double>(0, 1);
    int flag = inv ? -1 : 1;

    int bit_len = __lg(N); // log2
    CBigNum in(N);
    CBigNum out(N);

    for(int i=0;i<N;++i)
        in[bit_rev(i, bit_len)] = a[i];

    /* next page */

    if (inv) for(auto &c:in) c/=N;
    return in;
}

for(int n=2 ; n<=N ; n*=2)
{
    for(int base=0 ; base<N ; base+=n)
    {
        for(int i=0;i<n/2;++i)
        {
            auto wi = exp( flag * i * (2*PI/n) * I);
            out[base+i]     = in[base+i] + in[base+i+n/2] * wi;
            out[base+i+n/2] = in[base+i] - in[base+i+n/2] * wi;
        }
    }
    in.swap(out);
}

這個三層迴圈還有一些實作細節可以進一步優化，參見卦長模板

大數乘法投影片完整範例 : gist

練習題

https://asiahk16prel.kattis.com/problems/aplusb
hdu 1402
(C) https://codeforces.com/gym/100783/attachments
hdu 4609

進階主題 : 數論轉換，可以避免 FFT 的浮點誤差

Math Skill

By sylveon

Math Skill

2,508