Física
At mica

Sebastián Tabares

Pedro Rodriguez

Dairo Carrillo

¿Que es?

Aplicar la mecánica cuántica a los sistemas atómicos, mas que todo enfocarlo a el átomo de hidrógeno, que es el que se describe con mas presición

Introduccion

Espectros atómicos
Propiedades cuánticas átomo de hidrógeno
estado cuántico de las órbitas de los elementos
energía, espín, momento angular del electrón

Espectro Atómico de los gases

Espectro de línea discreto: Se observa cuando un gas a baja presión se somete a una descarga eléctrica.
Espectroscopia de emisión: Este espectro de línea discreto difiere en gran medida del arco iris continuo de colores observado cuando se examina un sólido resplandeciente con el mismo instrumento.

Espectros de emisión

\frac{1}{\lambda} = R_H (\frac{1}{2^3}-\frac{1}{n^2})

\frac{​ 1 ​ ​}{​ λ ​} = R ​ H ​ ​ (\frac{​ 1 ​ ​}{​ 2 ​ 3 ​ ​ ​} - \frac{​ 1 ​ ​}{​ n ​ 2 ​ ​ ​})

\frac{1}{\lambda} = R_H (1-\frac{1}{n^2})

\frac{​ 1 ​ ​}{​ λ ​} = R ​ H ​ ​ (1 - \frac{​ 1 ​ ​}{​ n ​ 2 ​ ​ ​})

\frac{1}{\lambda} = R_H (\frac{1}{3^2}-\frac{1}{n^2})

\frac{​ 1 ​ ​}{​ λ ​} = R ​ H ​ ​ (\frac{​ 1 ​ ​}{​ 3 ​ 2 ​ ​ ​} - \frac{​ 1 ​ ​}{​ n ​ 2 ​ ​ ​})

\frac{1}{\lambda} = R_H (\frac{1}{4^2}-\frac{1}{n^2})

\frac{​ 1 ​ ​}{​ λ ​} = R ​ H ​ ​ (\frac{​ 1 ​ ​}{​ 4 ​ 2 ​ ​ ​} - \frac{​ 1 ​ ​}{​ n ​ 2 ​ ​ ​})

Balmer

Lyman

Pacshen

Brackett

Espectros de Absorción

Modelos del Atómo

En la historia de la física

ha habido varios modelos atómicos

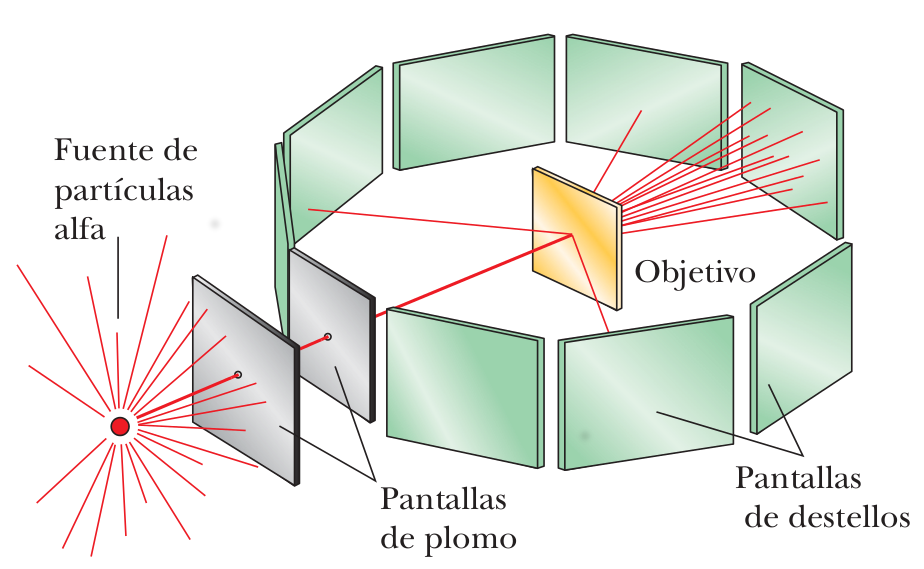
Modelo de Bohr

el electrón se mueve en órbitas circulares
solo ciertas órbitas son estables: estados estacionarios
solo la radiacion es emitida cuando cambia de una órbita de mayor energía a una menor

la frecuencia ƒ del
fotón emitida en la transición se relaciona con el cambio en la energía del átomo y
no es igual a la frecuencia del movimiento orbital del electrón

E_i = E_f = hf

E ​ i ​ ​ = E ​ f ​ ​ = h f

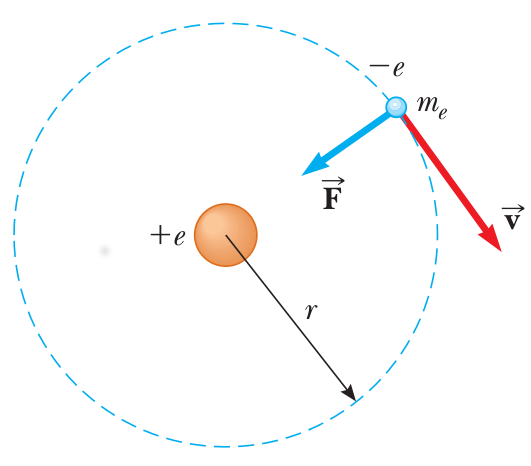
Cuantización Energía

La cuantización de los radios de la órbita conduce a la cuantización de la energía.

E_n = \frac{k_e e^2}{2a_0} \left( \frac{1}{n^2}\right) \ \ \ n = 1,2,3,\ldots

E ​ n ​ ​ = \frac{​ k ​ e ​ ​ e ​ 2 ​ ​ ​ ​}{​ 2 a ​ 0 ​ ​ ​} (\frac{​ 1 ​ ​}{​ n ​ 2 ​ ​ ​}) n = 1, 2, 3, \dots

E_n = - \frac{13.606 \ eV}{n^2} \ \ \ n = 1,2,3,\ldots

E ​ n ​ ​ = - \frac{​ 1 3 . 6 0 6 e V ​ ​}{​ n ​ 2 ​ ​ ​} n = 1, 2, 3, \dots

Frecuencia emisión fotón

Hidrógeno

f = \frac{E_i - E_f}{h} = \frac{k_ee^2}{2a_0h} \left(\frac{1}{n_f^2} -\frac{1}{n_i^2}\right)

f = \frac{​ E ​ i ​ ​ - E ​ f ​ ​ ​ ​}{​ h ​} = \frac{​ k ​ e ​ ​ e ​ 2 ​ ​ ​ ​}{​ 2 a ​ 0 ​ ​ h ​} (\frac{​ 1 ​ ​}{​ n ​ f ​ 2 ​ ​ ​} - \frac{​ 1 ​ ​}{​ n ​ i ​ 2 ​ ​ ​})

Modelo Cuántico

El modelo de Bohr no predice con exactitud todas nociones experimentales que se ven, por eso surge un modelo mas aproximado a la realidad

-\frac{h^2 }{2m} \frac{\partial^2 \Psi }{\partial x^2} +U \Psi = E \Psi

- \frac{​ h ​ 2 ​ ​ ​ ​}{​ 2 m ​} \frac{​ \partial ​ 2 ​ ​ Ψ ​ ​}{​ \partial x ​ 2 ​ ​ ​} + U Ψ = E Ψ

U(r) = - k_e \frac{e^2}{r}

U (r) = - k ​ e ​ ​ \frac{​ e ​ 2 ​ ​ ​ ​}{​ r ​}

k_e = 8.99 \times10^9 \frac{Nm^2} { C^2}

k ​ e ​ ​ = 8.99 \times 1 0 ​ 9 ​ ​ \frac{​ N m ​ 2 ​ ​ ​ ​}{​ C ​ 2 ​ ​ ​}

Ecuación de Onda de Schrödinger

-\frac{h^2}{2m} \left( \frac{\partial^2\Psi}{\partial x^2}+\frac{\partial^2\Psi}{\partial y^2}+\frac{\partial^2\Psi}{\partial z^2}\right) + U\Psi = E\Psi

- \frac{​ h ​ 2 ​ ​ ​ ​}{​ 2 m ​} (\frac{​ \partial ​ 2 ​ ​ Ψ ​ ​}{​ \partial x ​ 2 ​ ​ ​} + \frac{​ \partial ​ 2 ​ ​ Ψ ​ ​}{​ \partial y ​ 2 ​ ​ ​} + \frac{​ \partial ​ 2 ​ ​ Ψ ​ ​}{​ \partial z ​ 2 ​ ​ ​}) + U Ψ = E Ψ

Modelo Cuántico

E_n = \frac{k_e e^2}{2a_0} \left( \frac{1}{n^2}\right) \ \ \ n = 1,2,3,\ldots

E ​ n ​ ​ = \frac{​ k ​ e ​ ​ e ​ 2 ​ ​ ​ ​}{​ 2 a ​ 0 ​ ​ ​} (\frac{​ 1 ​ ​}{​ n ​ 2 ​ ​ ​}) n = 1, 2, 3, \dots

E_n = - \frac{13.606 \ eV}{n^2} \ \ \ n = 1,2,3,\ldots

E ​ n ​ ​ = - \frac{​ 1 3 . 6 0 6 e V ​ ​}{​ n ​ 2 ​ ​ ​} n = 1, 2, 3, \dots

\Psi (\rho, \theta, \phi) = R(r)f(\theta)g(\phi)

Ψ (ρ, θ, ϕ) = R (r) f (θ) g (ϕ)

Ejercicio

Para un átomo de hidrógeno determine los estados permitidos que
correspondan al número cuántico principal n = 2 y calcule las energías de
estos estados.

Funcion Onda

Hidrógeno

Describe de manera aproximada la posición probabilística del electrón

\Psi_{1s}(r) = \frac{1}{\sqrt{\pi a_0^3}}e^{-r/a_0}

Ψ ​ 1 s ​ ​ (r) = \frac{​ 1 ​ ​}{​ \sqrt ​ π a ​ 0 ​ 3 ​ ​ ​ ​ ​ ​} e ​ - r / a ​ 0 ​ ​ ​ ​

P(r)dr = |\psi|^2dV = |\psi|^24\pi r^2 dr

P (r) d r = ∣ ψ ∣ ​ 2 ​ ​ d V = ∣ ψ ∣ ​ 2 ​ ​ 4 π r ​ 2 ​ ​ d r

P_{1s}(r) = \left( \frac{4r^2}{a_0^3}\right) e^{-2r/a_0}

P ​ 1 s ​ ​ (r) = (\frac{​ 4 r ​ 2 ​ ​ ​ ​}{​ a ​ 0 ​ 3 ​ ​ ​}) e ​ - 2 r / a ​ 0 ​ ​ ​ ​

Interpretacion Fisíca

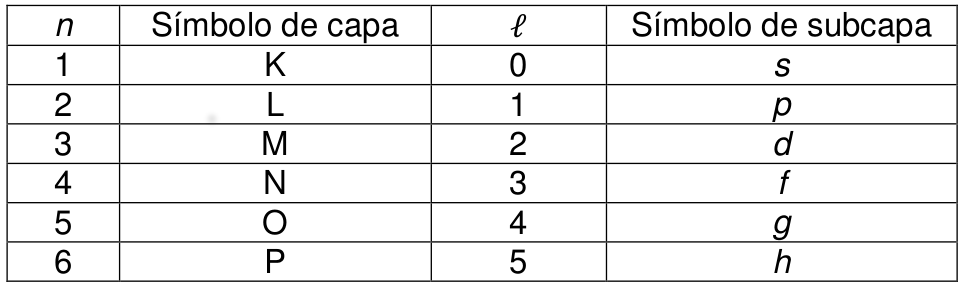
números Cuánticos

n \ l \ m_l

n l m ​ l ​ ​

Movimiento Angular

L = \sqrt{l(l+1)h^!} \ \ \ l = 0, 1, 2, \ldots, n-1

L = \sqrt ​ l (l + 1) h ​! ​ ​ ​ ​ ​ l = 0, 1, 2, \dots, n - 1

\vec{L}

​ L ​ ⃗ ​ ​

Espín?

El espín no viene de las ecuaciones de Schrödinger, se coloca ad-hoc

m_s

m ​ s ​ ​

S = \sqrt{(s(s+1)}h^! = \frac{\sqrt3}{2}h^!

S = \sqrt ​ (s (s + 1) ​ ​ ​ h ​! ​ ​ = \frac{​ \sqrt ​ 3 ​ ​ ​ ​ ​}{​ 2 ​} h ​! ​ ​

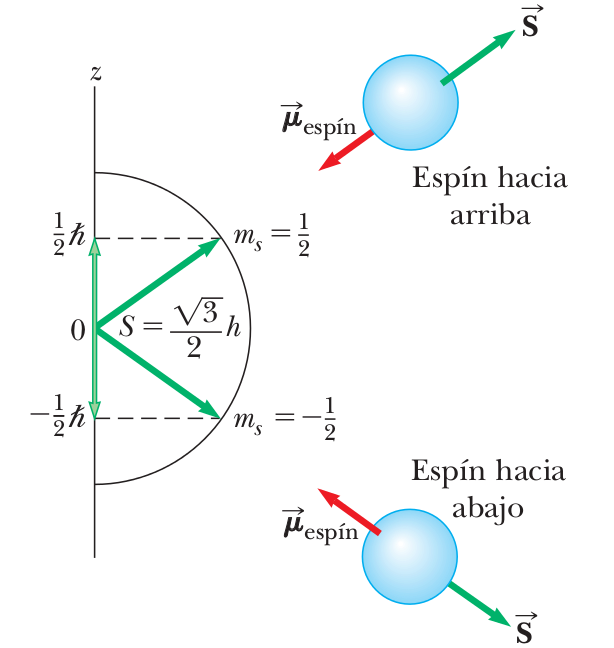
el espín está cuantizado

m_s = \pm \frac{1}{2}h^!

m ​ s ​ ​ = \pm \frac{​ 1 ​ ​}{​ 2 ​} h ​! ​ ​

Principio Exclusion Tabla periodica

No puede haber dos electrones en el mismo estado
cuántico; debido a eso, dos electrones del mismo
átomo no pueden tener el mismo conjunto de
números cuánticos.

PAULI

Definiciones

ORBITAL: Estado atómico caracterizado por los números cuánticos n, l, m l . Según
el principio de exclusión sólo puede haber dos electrones presentes en cualquier
orbital.
Uno de estos electrones tiene un número cuántico magnético de espín , y
el otro es .

m_s = \frac{1}{2}

m ​ s ​ ​ = \frac{​ 1 ​ ​}{​ 2 ​}

m_s = -\frac{1}{2}

m ​ s ​ ​ = - \frac{​ 1 ​ ​}{​ 2 ​}

Ejercicio

Encontrar los números cuánticos y la configuración electrónica de:

Berilio (z= 4).
Carbono (z= 6).

Física Atómica

By Sebastian Yesid Tabares Amaya

Física Atómica

Exposición sobre la física atómica

1,435

Física At mica

¿Que es?

Introduccion

Espectro Atómico de los gases

Espectros de emisión

Espectros de Absorción

Modelos del Atómo

En la historia de la física

ha habido varios modelos atómicos

Modelo de Bohr

Cuantización Energía

Frecuencia emisión fotón

Hidrógeno

Modelo Cuántico

Modelo Cuántico

Ejercicio

Funcion Onda

Hidrógeno

Interpretacion Fisíca

números Cuánticos

Movimiento Angular

Espín?

Principio Exclusion Tabla periodica

Definiciones

Ejercicio

Física Atómica

More from Sebastian Yesid Tabares Amaya

Física
At mica