H.J. Terry Suh
Leveraging Structure for Efficient and Dexterous Contact-Rich Manipulation
Thesis Defense
Committee: Russ Tedrake (Advisor),
Tomas Lozano-Perez, Marc Toussaint, Justin Carpentier

Part 3. Global Planning for Contact-Rich Manipulation
Part 2. Local Planning for Contact-Rich Manipulation
Part 1. Contact Mode Abstraction via Smoothing
Introduction


Manipulation: An Important Problem

Matt Mason, "Towards Robotic Manipulation", 2018
Manipulation: An Important Problem

Matt Mason, "Towards Robotic Manipulation", 2018
Manipulation is a core capability for robots to broaden the spectrum of things we can automate in this world.



DexAI
TRI Dishwasher Demo

Flexxbotics
ETH Zurich, Robotic Systems Lab
What is Contact-Rich Manipulation?
Manipulation that strategically makes decisions about contact after considering multiple possible ways of selecting contact, especially when such possibilities are many.
Contact-Rich Manipulation
H.J. Terry Suh, PhD Thesis

Matt Mason, "Towards Robotic Manipulation", 2018
What is Contact-Rich Manipulation?
Manipulation that strategically makes decisions about contact after considering multiple possible ways of selecting contact, especially when such possibilities are many.
Contact-Rich Manipulation
H.J. Terry Suh, PhD Thesis

What is Contact-Rich Manipulation?
Manipulation that strategically makes decisions about contact after considering multiple possible ways of selecting contact, especially when such possibilities are many.
Contact-Rich Manipulation
H.J. Terry Suh, PhD Thesis

What is Contact-Rich Manipulation?

- Where do I make contact?
- Where should I avoid contact?
- With what timing?
- What do I do after making contact?
Manipulation that strategically makes decisions about contact after considering multiple possible ways of selecting contact, especially when such possibilities are many.
Contact-Rich Manipulation
H.J. Terry Suh, PhD Thesis
What is Contact-Rich Manipulation?
As possibilities become many, strategic decisions become harder.


- Where do I make contact?
- Where should I avoid contact?
- With what timing?
- What do I do after making contact?
Manipulation that strategically makes decisions about contact after considering multiple possible ways of selecting contact, especially when such possibilities are many.
Contact-Rich Manipulation
H.J. Terry Suh, PhD Thesis
Case 1. Whole-Body Manipulation

Do not make contact
(Collision-free Motion Planning)
Make Contact
Human
Robot
Slide inspired by Tao Pang's Thesis Defense & TRI Punyo Team

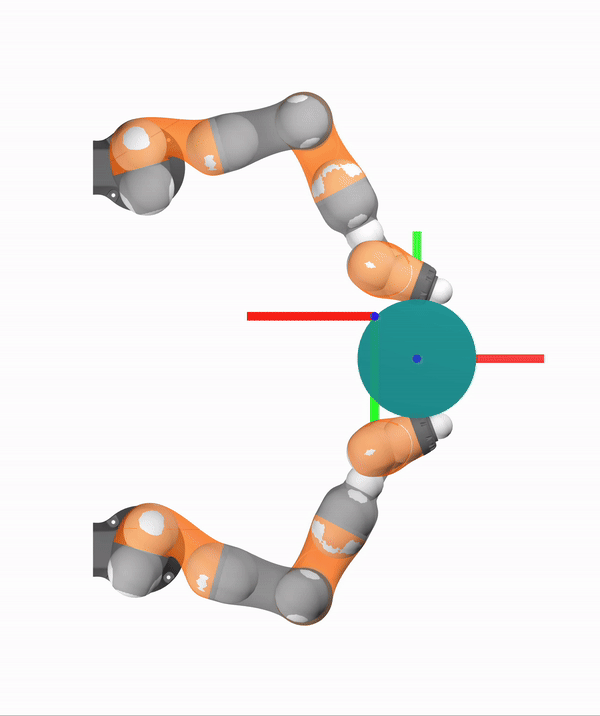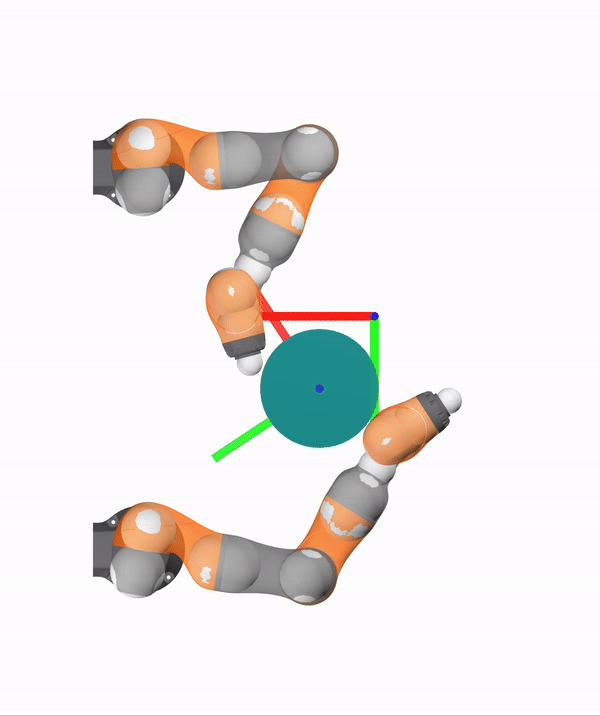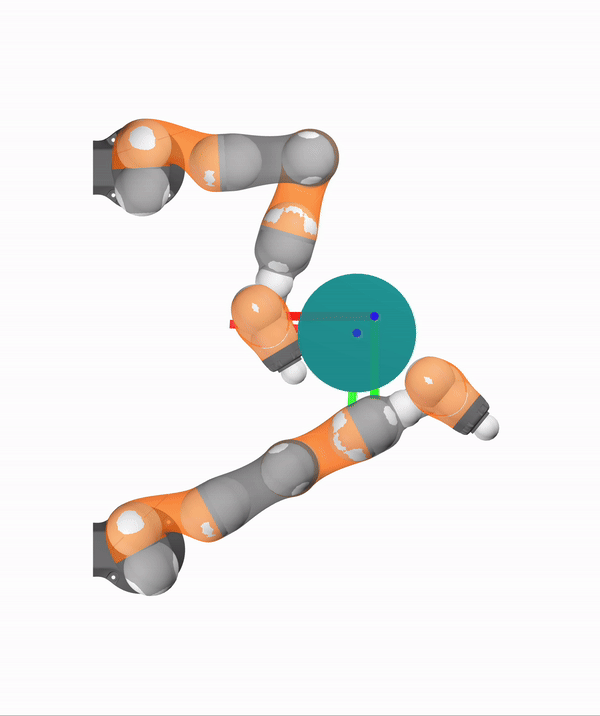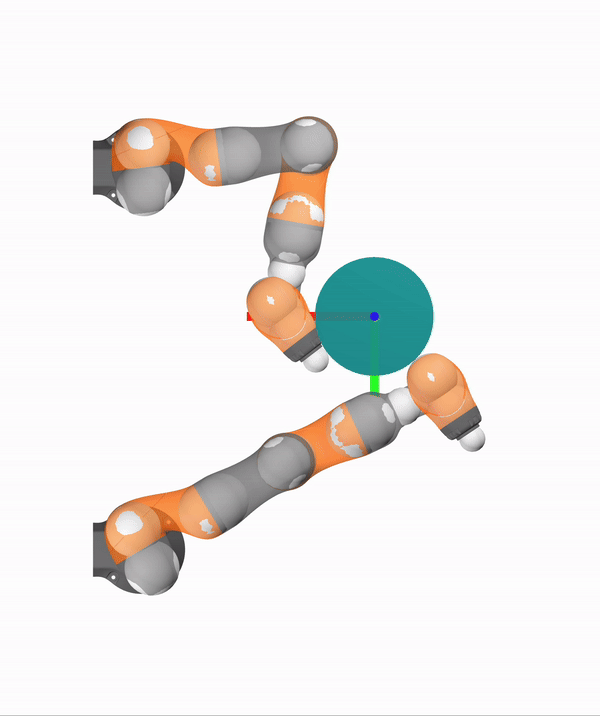
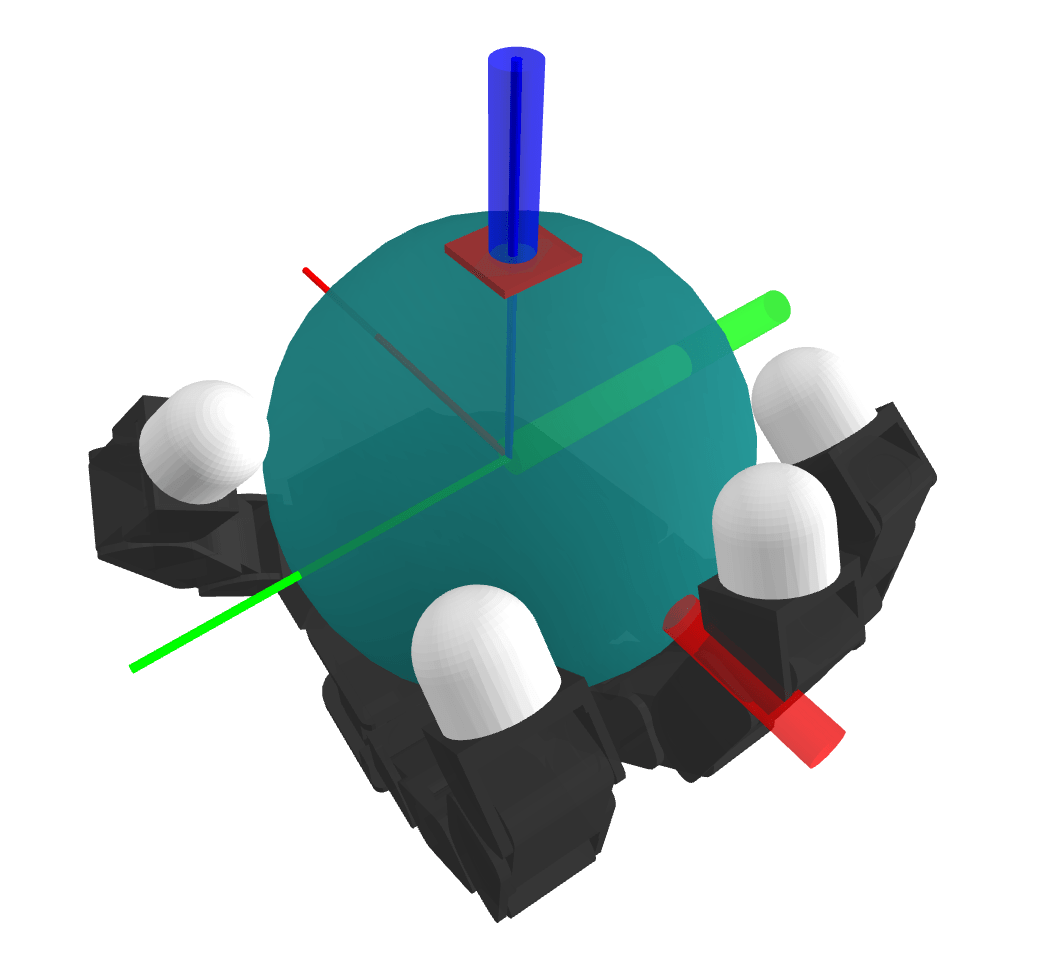
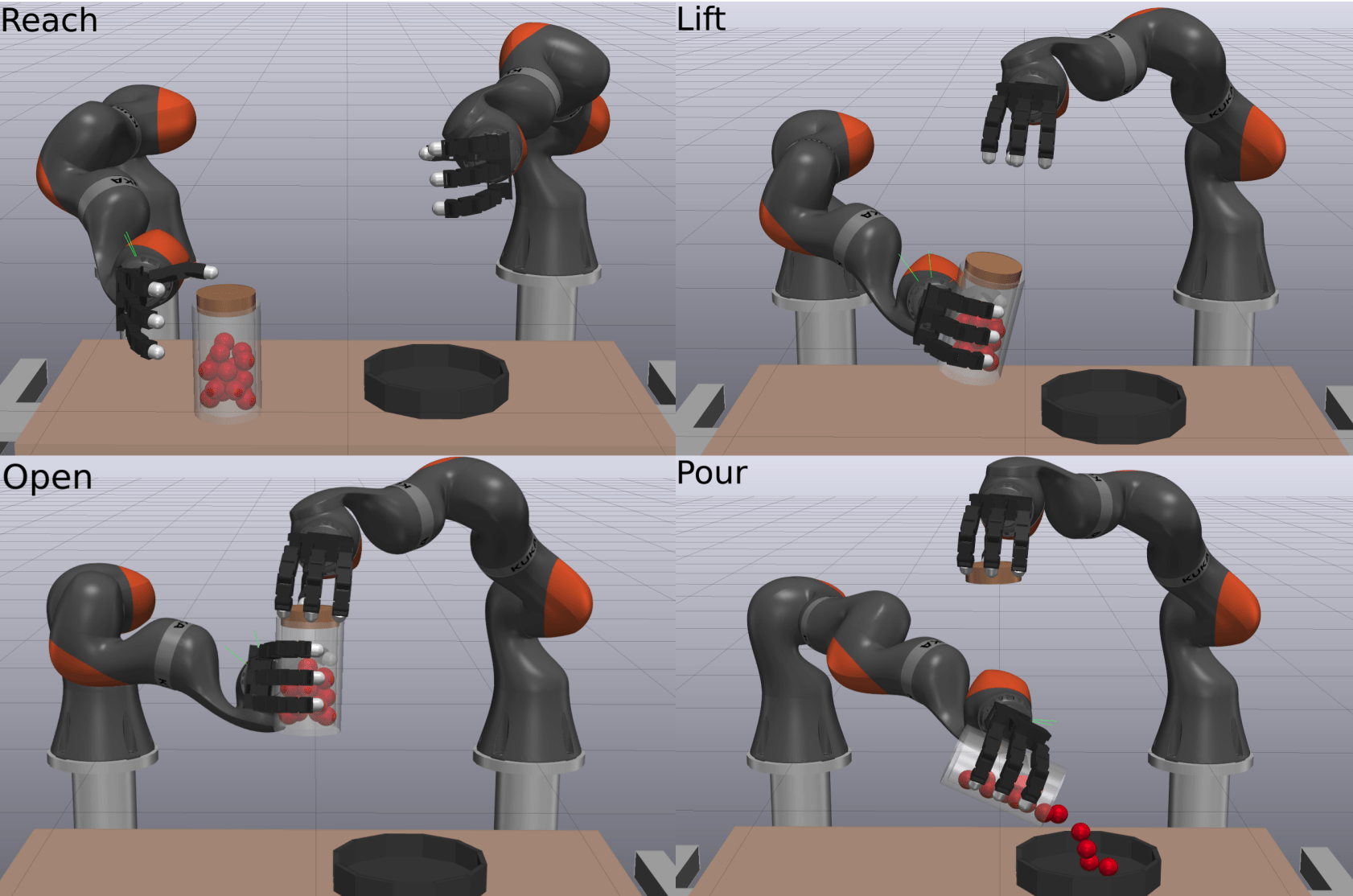
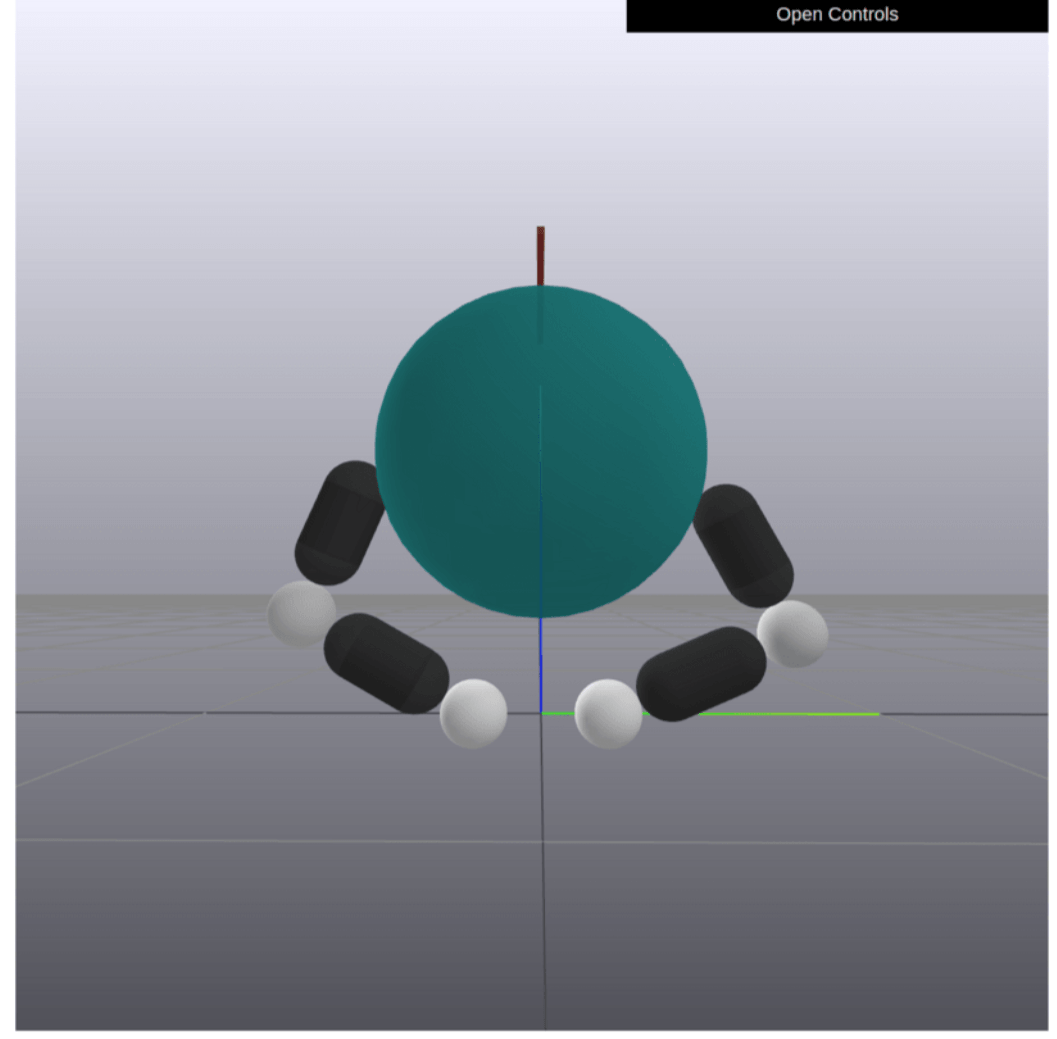
Case 2. Dexterous Manipulation
Human
Robot

Wonik Allegro Hand

Make Contact
Why Contact-Rich Manipulation?
A capable embodied intelligence must be able to exploit its physical embodiment to the fullest.
Manipulation that strategically makes decisions about contact after considering multiple possible ways of selecting contact, especially when such possibilities are many.
Contact-Rich Manipulation
H.J. Terry Suh, PhD Thesis
Fundamental Challenges

Fundamental Challenges

Fundamental Challenges

Fundamental Challenges

Fundamental Challenges

Fundamental Challenges

Fundamental Challenges

Fundamental Challenges

Fundamental Challenges

Smooth Analysis

Flatness and Stiffness spells difficulty for local gradient-based optimizers.
Smooth Analysis
But GIVEN a contact event, the landscape is smooth.


[Salisbury Hand, 1982]
[Murray, Li, Sastry]

What can we do given a contact mode?
Smooth Planning & Control
Combinatorial Optimization
Can we try to globally search for the right "piece"?

Hybrid Dynamics & Combinatorial Optimization
[Hogan et al., 2019]
[Graesdal et al., 2024]
Problems with Mode Enumeration
System
Number of Modes
No Contact
Sticking Contact
Sliding Contact
Number of potential active contacts
Problems with Mode Enumeration


System
Number of Modes
The number of modes scales terribly with system complexity
No Contact
Sticking Contact
Sliding Contact
Number of potential active contacts
Contact Relaxation & Smooth NLP
[Posa et al., 2013]
[Mordatch et al., 2012]
Reinforcement Learning
[OpenAI et al., 2019]
[Handa et al., 2024]
Reinforcement Learning
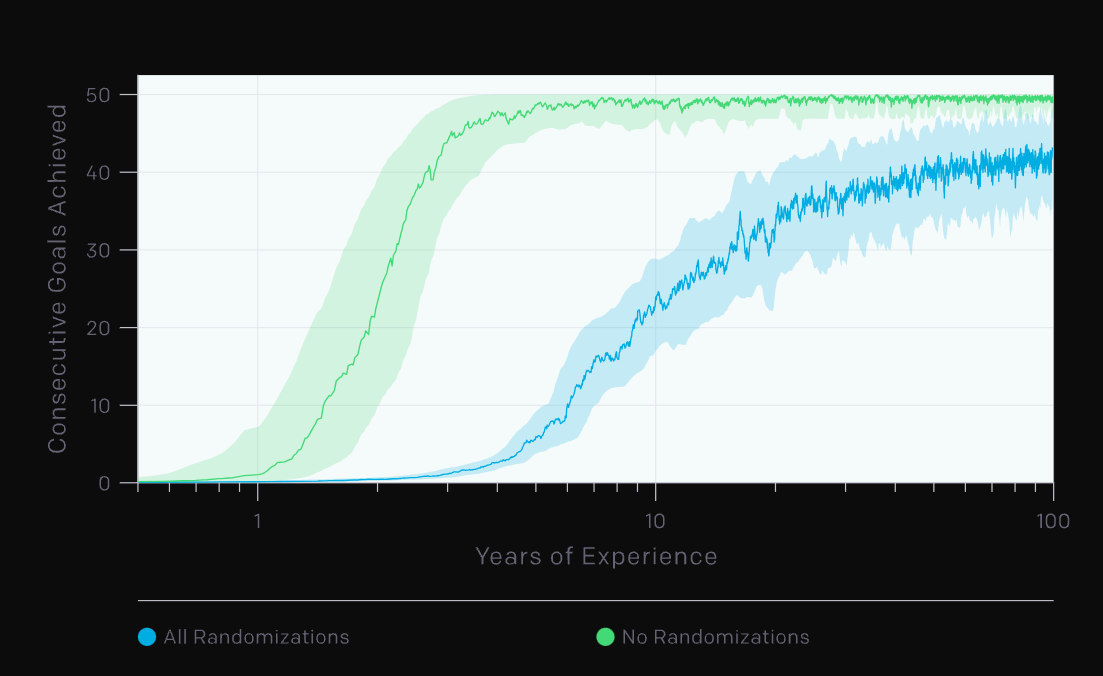
[OpenAI et al., 2019]
Summary of Previous Approaches
Classical Mechanics
Hybrid Dynamics &
Combinatorial Optimization
Contact Relaxation &
Smooth Nonlinear Programming
Reinforcement Learning
Contact Scalability
Efficiency
Global Scope












Summary of Previous Approaches
Classical Mechanics
Hybrid Dynamics &
Combinatorial Optimization
Contact Relaxation &
Smooth Nonlinear Programming
Reinforcement Learning
Contact Scalability
Efficiency
Global Scope












How can we achieve all three criteria?
Preview of Results
Our Method


Contact Scalability
Efficiency
Global Scope

60 hours, 8 NVidia A100 GPUs
5 minutes, 1 Macbook M3 CPU

[TRO 2023, TRO 2025]
Part 3. Global Planning for Contact-Rich Manipulation
Part 2. Local Planning for Contact-Rich Manipulation
Part 1. Contact Mode Abstraction via Smoothing
Introduction



[TRO 2023, TRO 2025]
Part 1. Contact Mode Abstraction via Smoothing
Introduction



Part 3. Global Planning for Contact-Rich Manipulation
Part 2. Local Planning for Contact-Rich Manipulation
[TRO 2023, TRO 2025]
Part 1. Contact Mode Abstraction via Smoothing
What allows abstraction of contact modes?
How can we achieve it efficiently?
[RA-L 2021, ICML 2022, TRO 2023]
Summary of Previous Approaches
Classical Mechanics
Hybrid Dynamics &
Combinatorial Optimization
Contact Relaxation &
Smooth Nonlinear Programming
Reinforcement Learning
Contact Scalability
Efficiency
Global Scope












How do these methods abstract contact modes?
Reinforcement Learning
Stochastic & Discrete


Deterministic & Continuous
Reinforcement Learning
Stochastic & Discrete


Deterministic & Continuous
But why does RL actually work on
continuous, seemingly deterministic problems?
Reinforcement Learning
Stochastic & Discrete


Deterministic & Continuous
RL considers a stochastic objective / policy
[RA-L 2021, ICML 2022]
How does RL abstract contact modes?
[ICML 2022]

How does RL abstract contact modes?
[ICML 2022]

How does RL abstract contact modes?
[ICML 2022]

How does RL abstract contact modes?
[ICML 2022]

How does RL abstract contact modes?
[ICML 2022]

How does RL abstract contact modes?
[ICML 2022]

How does RL abstract contact modes?
[ICML 2022]

How does RL abstract contact modes?
[ICML 2022]

How does RL abstract contact modes?
[ICML 2022]

How does RL abstract contact modes?
[ICML 2022]

Randomized Smoothing
[ICML 2022]


Noise regularizes difficult landscapes,
allevates flatness and stiffness
Randomized Smoothing
[ICML 2022]


Noise regularizes difficult landscapes,
allevates flatness and stiffness
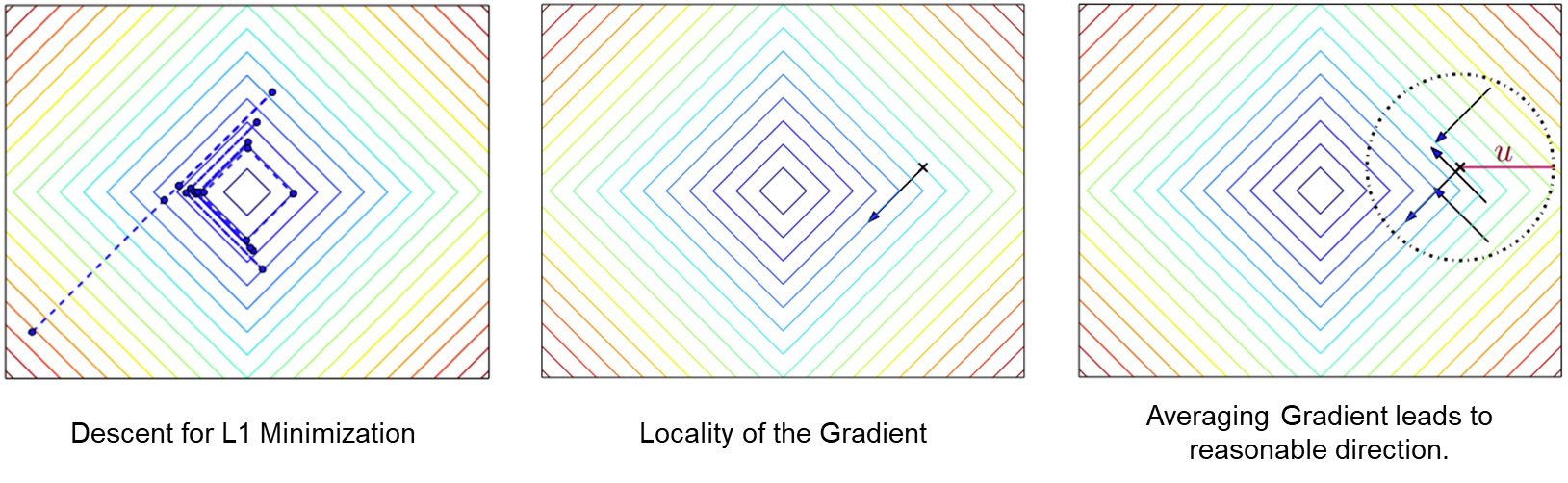
[Duchi et al, 2012]
Contact Mode Abstraction via Sampling

Thumb Only
Thumb and index
Ring Only
Thumb, Index, Ring
[RA-L 2021, TRO 2023]
Contact Mode Abstraction via Sampling


Thumb Only
Thumb and index
Ring Only
Thumb, Index, Ring
[RA-L 2021, TRO 2023]
Contact Mode Abstraction via Sampling


Thumb Only
Thumb and index
Ring Only
Thumb, Index, Ring
[RA-L 2021, TRO 2023]
Contact Mode Abstraction via Sampling


Relu 1,5 Active
Relu 0,1,5 Active
ReLU 0,1 Active
ReLU 0 Active
[RA-L 2021, TRO 2023]
Contact Mode Abstraction via Sampling


Deep Reinforcement Learning
Randomized Smoothing in Non-smooth Optimization

[RA-L 2021]
[ICML 2022]
[Duchi et al, 2012]
[Schulman et al, 2015]

[TRO 2023]

[Le Lidec et al, 2024]
[TRO 2023, TRO 2025]
Part 1. Contact Mode Abstraction via Smoothing
What allows abstraction of contact modes?
How can we achieve it efficiently?

[RA-L 2021, ICML 2022, TRO 2023]
Towards Efficiency
How can we abstract contact modes more efficiently?
Towards Efficiency
How can we abstract contact modes more efficiently?
- Using Gradients
Towards Efficiency
How can we abstract contact modes more efficiently?
- Using Gradients
2. Without Monte-Carlo

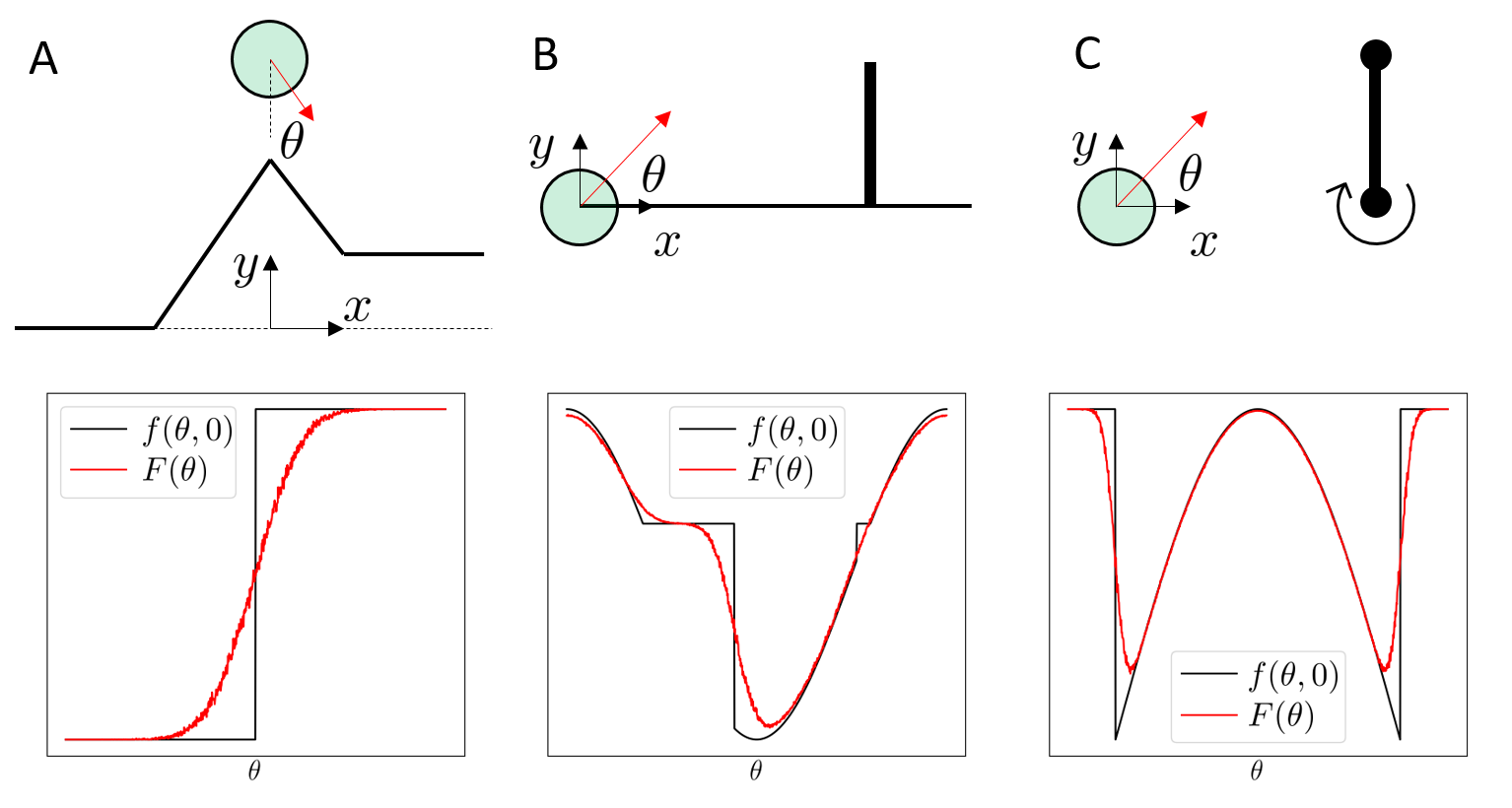
Intuitive Physics of Contact
Where will the box move next?
Intuitive Physics of Contact

Where will the box move next?
Intuitive Physics of Contact

Intuitive Physics of Contact
Intuitive Physics of Contact


Simulations should be constraint-driven
Intuitive Physics of Contact
Intuitive Physics of Contact
Intuitive Physics of Contact


Did we think about velocities at all?
Or purely reason about configuration?
Quasistatic Modeling & Optimization-Based Sim.
Optimization-Based Simulation
Quasistatic Modeling
[Stewart & Trinkle, 2000]
[Mujoco, Todorov 2012]
[SAP Solver (Drake), CPH, 2022]
[Dojo, HCBKSM 2022]
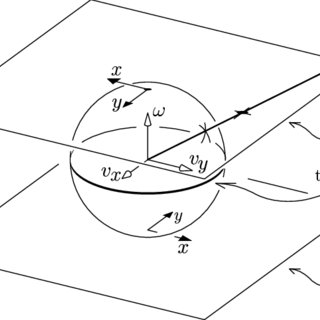

[Howe & Cutkosky 1996]
[Lynch & Mason 1996]
[Halm & Posa 2018]
[Pang & Tedrake 2021]
CQDC: A Quasi-dynamic Simulator for Manipulation

Dr. Tao Pang
Robot commands as
State only comprises of configurations
- Actuated configurations (Robot)
- Unactuated configurations (Object)
- Position command to an stiffness controller





Convex
Quasidynamic
Differentiable
Contact Model

[TRO 2023]
CQDC: A Quasi-dynamic Simulator for Manipulation
[TRO 2023]
CQDC: A Quasi-dynamic Simulator for Manipulation
[TRO 2023]
CQDC: A Quasi-dynamic Simulator for Manipulation
Non-Penetration
Minimum Energy Principle
[TRO 2023]
CQDC as Convex Optimization
[TRO 2023]
Second-Order Cone Program (SOCP)

We can use standard SOCP solvers to solve this program
Sensitivity Analysis
[TRO 2023]
Second-Order Cone Program (SOCP)

Allows gradient computations after solving optimization

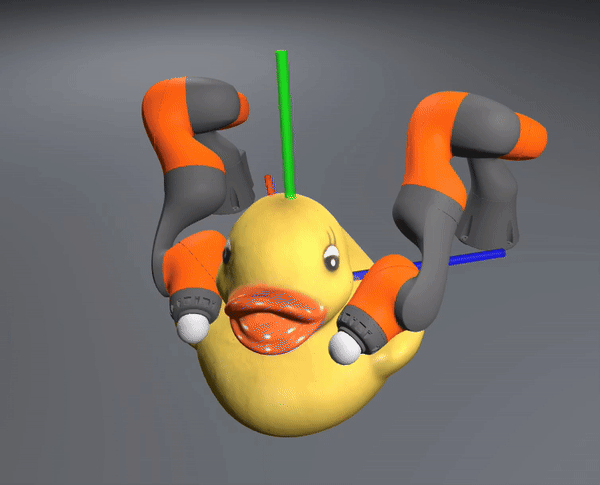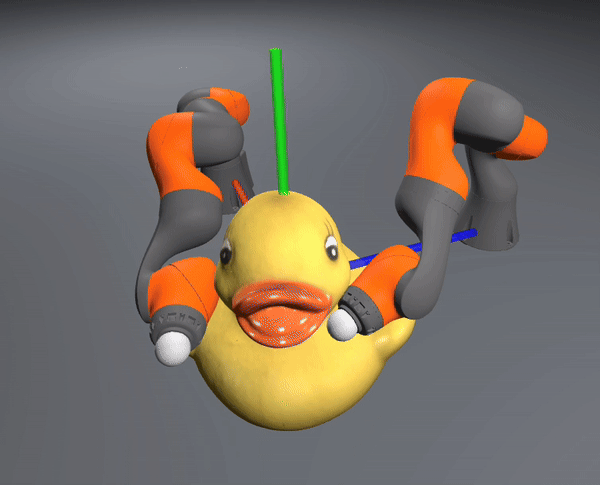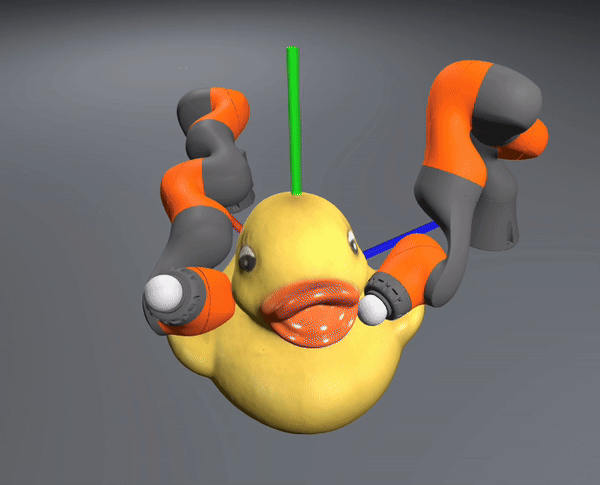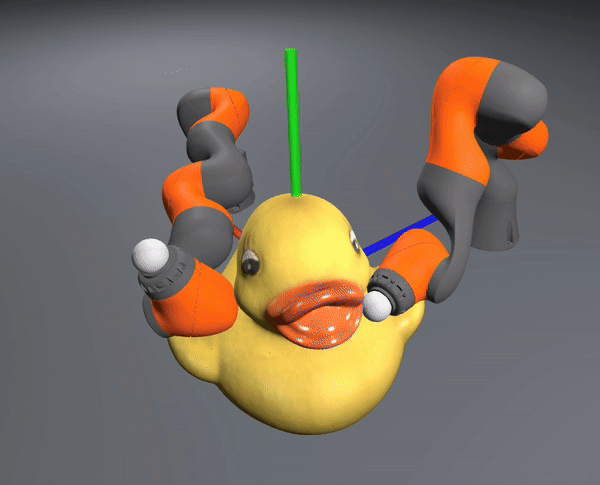

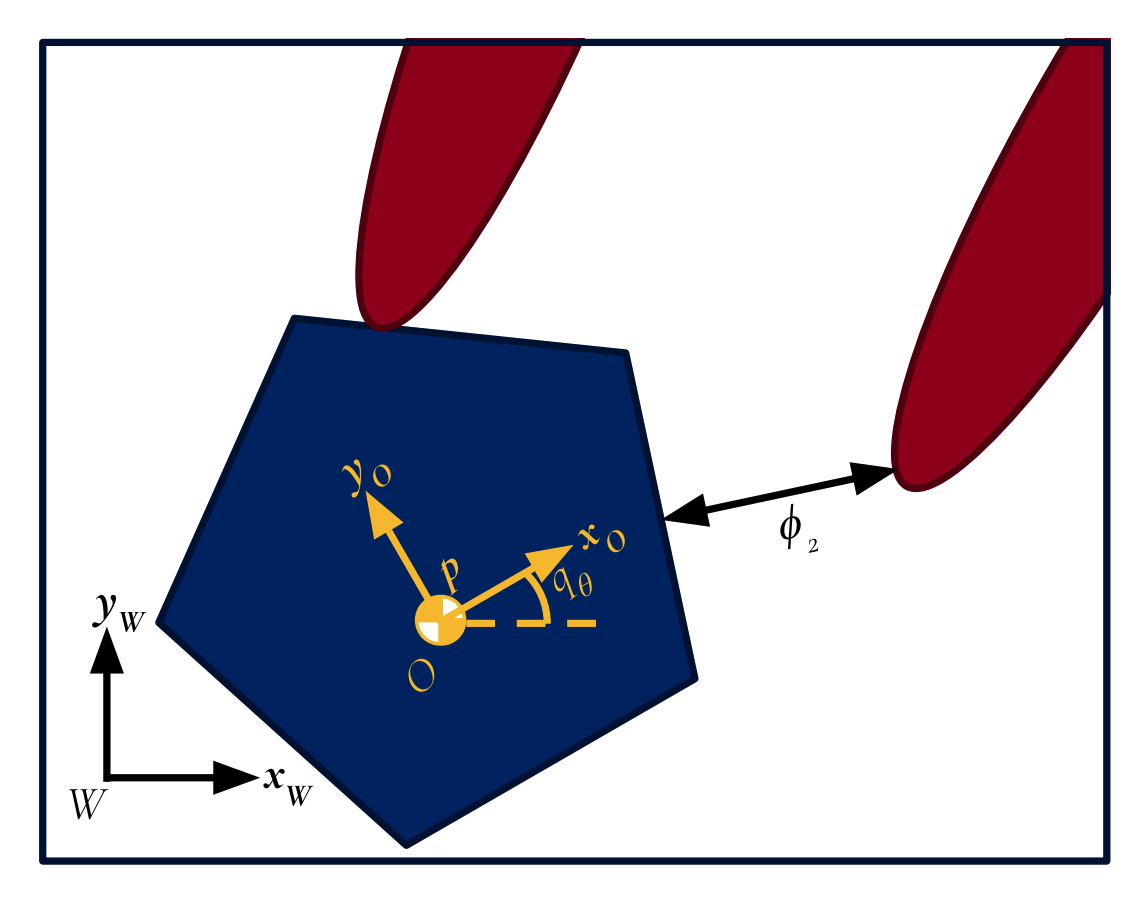
Uses Drake as Backbone

Allows us to separate complexity of "contact" from complexity of "highly dynamic".
CQDC Simulator

[TRO 2023]
Smoothing of Optimization-Based Simulators
How do we abstract contact for optimization-based simulation?
[TRO 2023]


Thumb Only
Thumb and index
Ring Only
Thumb, Index, Ring
Randomized-Smoothed Dynamics


Initial Configuration
1-Step Dynamics
Sampling
[RA-L 2021, TRO 2023]
Constrained Optimization
[TRO 2023]
Constrained Optimization

[TRO 2023]
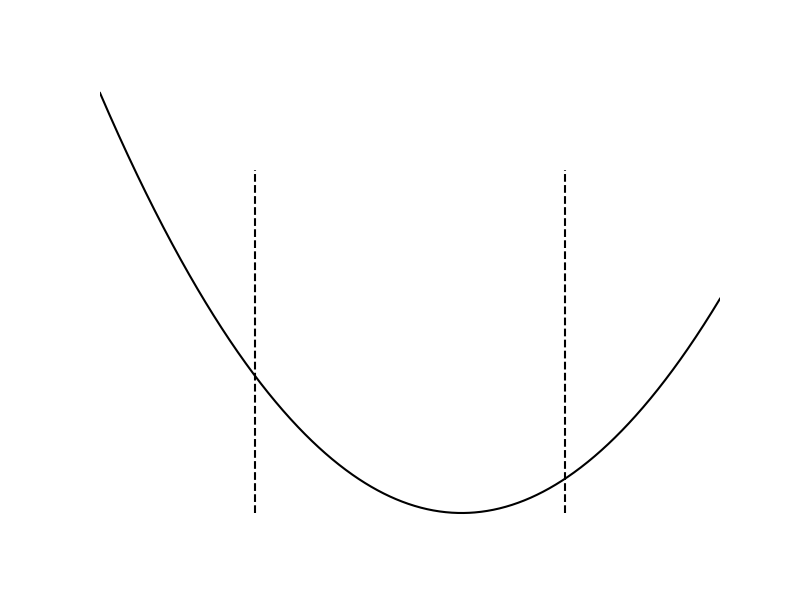
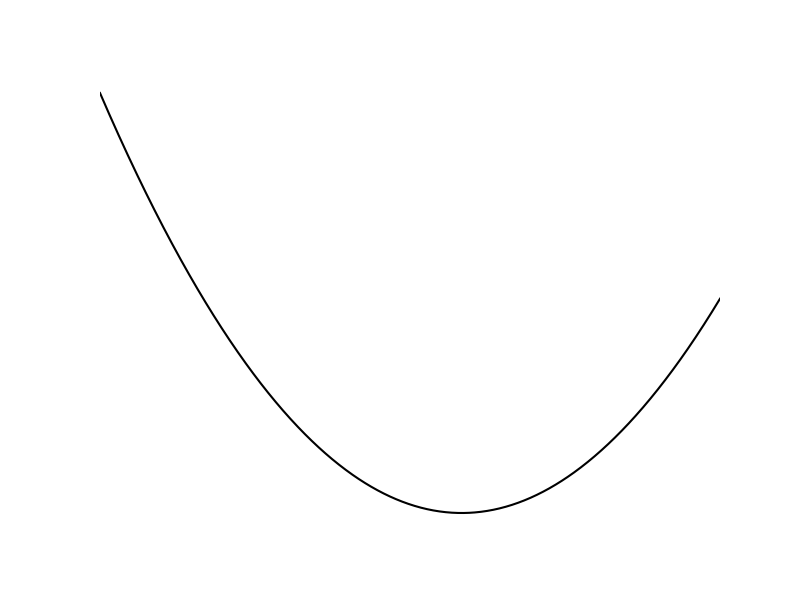
Log-Barrier Relaxation





[TRO 2023]
Log-Barrier Relaxation





Constraints have an inversely proportional effect to distance.
[TRO 2023]
Barrier-Smoothed Dynamics


Initial Configuration
1-Step Dynamics
(Low Smoothing)

1-Step Dynamics
(High Smoothing)
Barrier smoothing creates force from a distance
[TRO 2023]
Equivalence of Smoothing Schemes

The two smoothing schemes are equivalent!
(There is a distribution that corresponds to barrier smoothing)

Randomized Smoothing

Barrier Smoothing
[TRO 2023]
Equivalence of Smoothing Schemes

The two smoothing schemes are equivalent!
(There is a distribution that corresponds to barrier smoothing)

Randomized Smoothing

Barrier Smoothing
[TRO 2023]
No Monte Carlo + First Order
Monte Carlo + Zeroth Order
Contributions
Barrier Smoothing

[HCBKSM 2022]

[OLP 2019]

[PCT 2015]

[TRO 2024]

[TRO 2024]

[ZJW 2023]
Equivalence
LCP Relaxation

[RA-L 2022]

[MSLSMC, 2024]
Randomized Smoothing
Part 1. Contact Mode Abstraction via Smoothing
What allows abstraction of contact modes?
How can we achieve it efficiently?

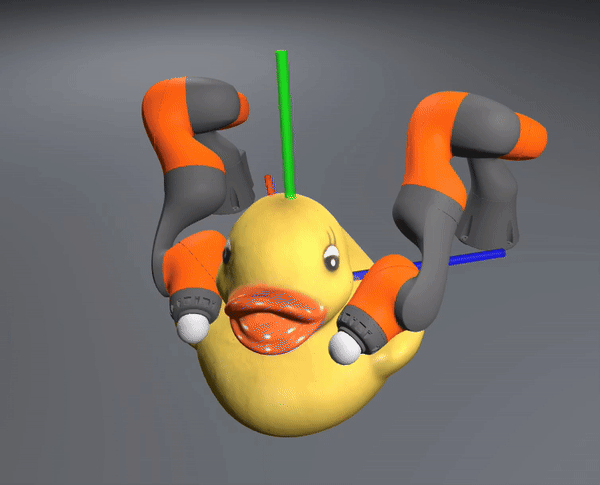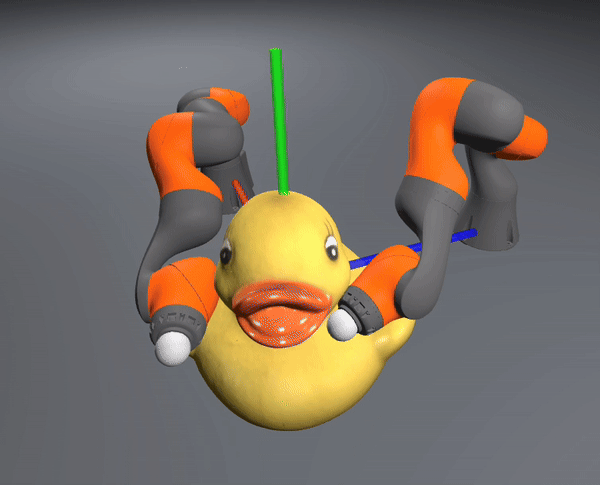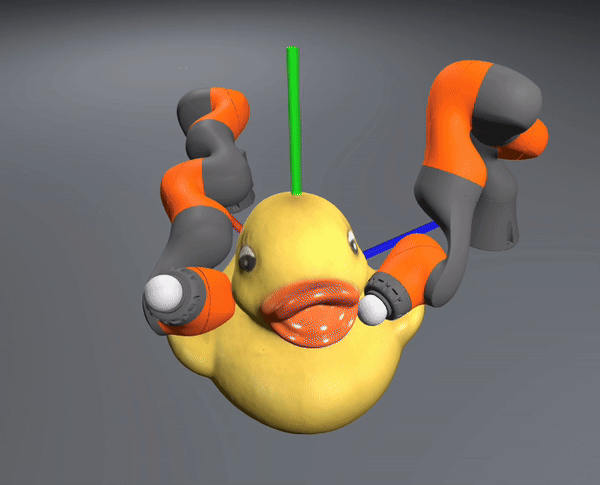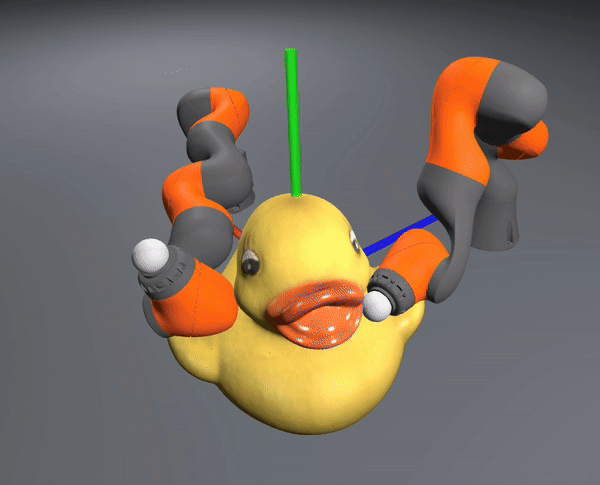

Can take gradients efficiently



Doesn't require Monte Carlo
[RA-L 2021, ICML 2022, TRO 2023]
Part 3. Global Planning for Contact-Rich Manipulation
Part 2. Local Planning for Contact-Rich Manipulation
Part 1. Contact Mode Abstraction via Smoothing
Introduction



[TRO 2023, TRO 2025]
Part 2. Local Planning for Contact-Rich Manipulation
What is a good local model of contact dynamics?
How do we enable local gradient-based planning?
[TRO 2023, TRO 2025 (WIP)]
Dynamics


Dynamics Equation



Dynamics





Dynamics Equation
Dynamics





Dynamics Equation
Dynamics





How should I command the robot to move the object to some goal?
Planning & Control
Get to the goal
Minimize effort

Dynamics Equation
Planning & Control
Get to the goal
Minimize effort

This problem is nonlinear....how do we tackle it with iterative optimization?
Planning & Control
Dynamics Equation
Sampling-Based Strategy
Dynamics



Sampling-Based Strategy

Sampling-Based Strategy




Get to the goal
Minimize effort
Feasible Set
Planning & Control
How do we represent this set in a computationally tractable manner?
- Using Gradients
2. Without Monte-Carlo

Planning & Control
How do we represent this set in a computationally tractable manner?
Attempt 1.
Taylor Approximation
Iterative Optimization for Planning
Get to the goal
Minimize effort
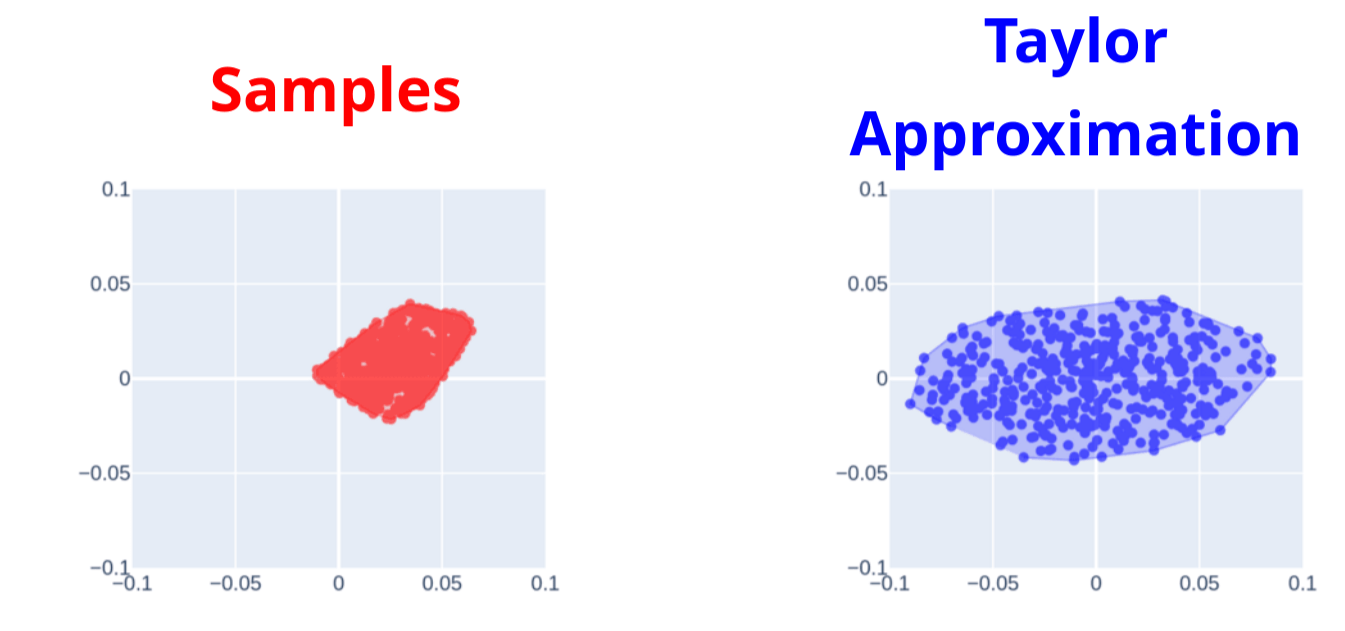
First-Order Taylor Approximation
Trust Region
Now a convex optimization problem!
Linearized Dynamics




Local Model over the Dynamics
Trust Region


True Samples
Samples from Local Model
Linear Map
Dynamics
Local Model over the Dynamics
Trust Region
Existing Literature
QP Controllers
iLQR & DDP
[Kuindersma et al., 2014]


[Kong et al., 2023]

[Tassa et al., 2014]

[Farshidian et al., 2017]
MPC Controllers
iLQR & DDP

[Kim et al., 2019]
[Tassa et al., 2014]

[Sleileman et al., 2021]
Local Model with Smoothing
True Dynamics
First-Order Taylor Approximation
robot
object
robot
object
Planning & Control
How do we represent this set in a computationally tractable manner?
Attempt 1.
Taylor Approximation
Attempt 2.
Taylor Approximation
on Smoothed Dynamics
Local Model with Smoothing
Smoothed Dynamics
First-Order Taylor Approximation
robot
object
robot
object
Iterative Optimization for Planning
Get to the goal
Minimize effort
First-Order Taylor Approximation
Trust Region

Local Model is too myopic

Iterative Optimization for Planning
Get to the goal
Minimize effort
First-Order Taylor Approximation
Trust Region
Provides a slightly more global model


Existing Literature

[Howell, Le Cleach et al., 2022]

[Suh et al., 2022]

[Shirai et al., 2024]

[Pang et al., 2023]
Contact Relaxation

[Huang et al., 2021]

[Turpin et al., 2023]



True Samples
Samples from Local Model
Linear Map
Dynamics
Is our local model correct?
Trust Region
[TRO 2025 (WIP)]



True Samples
Samples from Local Model
Linear Map
Dynamics
Is our local model correct?
What are we missing here?
Trust Region
[TRO 2025 (WIP)]
Planning & Control
How do we represent this set in a computationally tractable manner?
Attempt 1.
Taylor Approximation
Attempt 2.
Taylor Approximation
on Smoothed Dynamics
Attempt 3.
Friction Cone Constraints
on Dual Linearization
Local Model with Smoothing
Smoothed Dynamics
First-Order Taylor Approximation
robot
object
robot
object
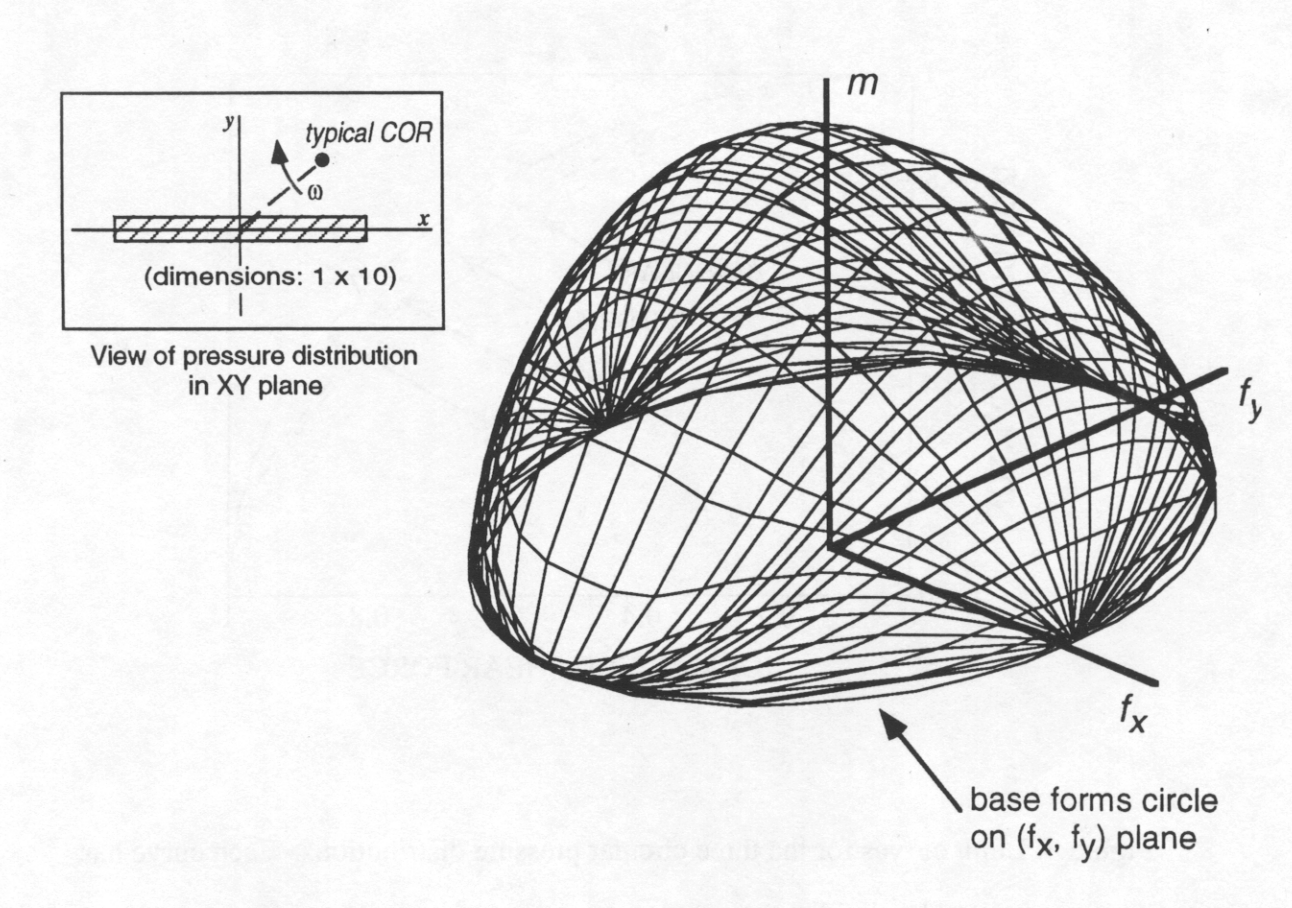
Friction Cone
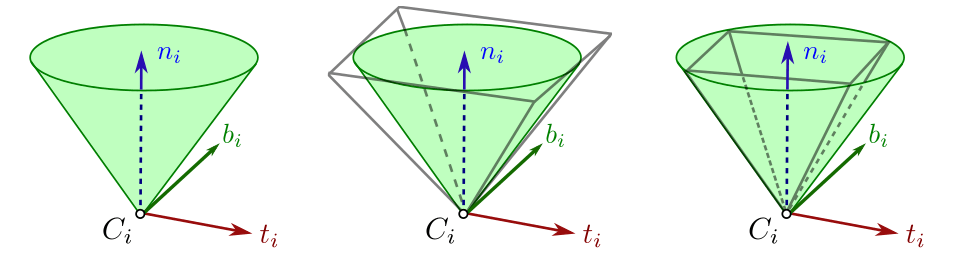
*image taken from Stephane Caron's blog
Unilateral
(Can't pull)
Coulomb Friction
Friction Cone
+
=
[TRO 2025 (WIP)]
Friction Cone

*image taken from Stephane Caron's blog
Unilateral
(Can't pull)
Coulomb Friction
Friction Cone
+
=
But how do we reason about constraints on contact impulses?
[TRO 2025 (WIP)]
Iterative Optimization for Planning
Get to the goal
Minimize effort
First-Order Taylor Approximation
Trust Region
We need an expression for contact impulses
[TRO 2025 (WIP)]
CQDC: A Quasi-dynamic Simulator for Manipulation
Non-Penetration
Minimum Energy Principle
[TRO 2025 (WIP)]
CQDC: A Quasi-dynamic Simulator for Manipulation
Stationarity Condition
Contact Impulse
Contact Jacobian
Object Movement
The Dual Variables become Contact Impulse
[TRO 2025 (WIP)]
CQDC as Convex Optimization
Second-Order Cone Program (SOCP)

Primal Solution (Configuration)
Dual Solution (Contact Impulse)
[TRO 2025 (WIP)]
Sensitivity Analysis over Dual Variables
Second-Order Cone Program (SOCP)

Primal Gradient (Configuration)
Dual Gradient (Contact Impulse)
[TRO 2025 (WIP)]
The Contact Impulse Map
Dynamics (Primal)


Contact Impulses (Dual)


Trust Region
[TRO 2025 (WIP)]
Dynamics (Primal)


Contact Impulses (Dual)


The Contact Impulse Map
Trust Region
[TRO 2025 (WIP)]
Qualification on Contact Impulses


Contact Impulses (Dual)



Dynamics (Primal)
+
Trust Region
[TRO 2025 (WIP)]
Qualification on Contact Impulses


Contact Impulses (Dual)



+
Some samples violate friction cone constraints!
Dynamics (Primal)
Trust Region
[TRO 2025 (WIP)]
Feasible Trust Region
Dynamics (Primal)
Contact Impulses (Dual)
Trust Region Size
Feasible Trust Region
[TRO 2025 (WIP)]
Motion Set
Feasible Trust Region


Motion Set

Dynamics (Primal)
Contact Impulses (Dual)
Trust Region Size
Feasible Trust Region
[TRO 2025 (WIP)]
Contact Impulse Set
Feasible Trust Region

Contact Impulse Set

Dynamics (Primal)
Contact Impulses (Dual)
Trust Region Size
[TRO 2025 (WIP)]
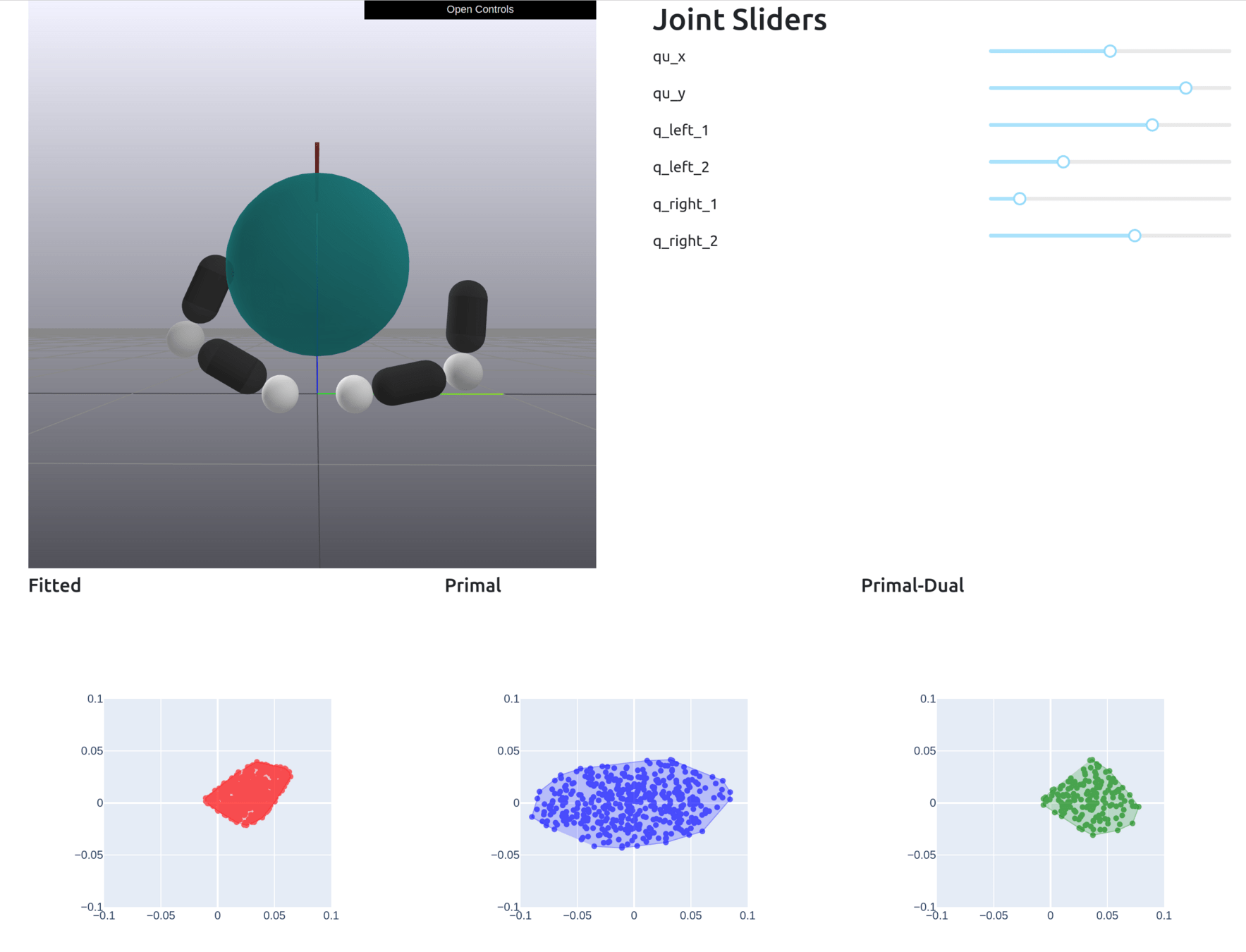
Now we have a close match with real samples
Motion Set
No Constraints
True Samples
[TRO 2025 (WIP)]
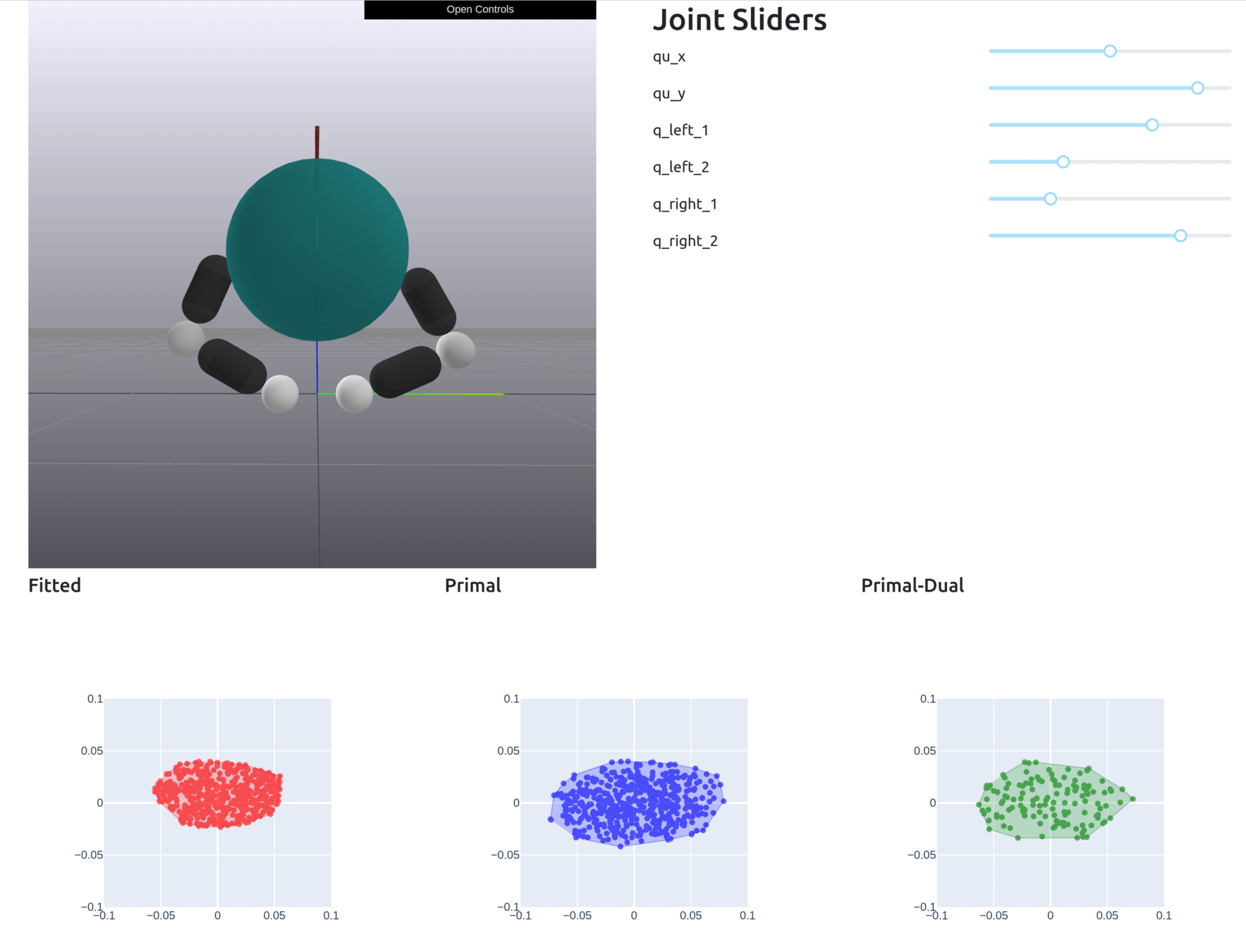
Motion Set
No Constraints
True Samples
Closer to ellipse when there is a full grasp
[TRO 2025 (WIP)]

The gradients take into account manipulator singularities
Motion Set
No Constraints
True Samples
[TRO 2025 (WIP)]

[OLP 2019]

[PCT 2015]


[Howell, Le Cleach et al., 2022]

[Pang et al., 2023]
Differentiable Simulator
Feasible Trust Region
Model Predictive Control
[Kuindersma et al., 2014]


[Farshidian et al., 2017]

[Kim et al., 2019]

[Sleileman et al., 2021]

[Aydinoglu et al., 2021]


[TRO 2025 (WIP)]
[TRO 2023, TRO 2025]
Part 2. Local Planning for Contact-Rich Manipulation
What is a good local model of contact dynamics?
How do we enable local gradient-based planning?

Finding Optimal Action: One Step
Get to the goal
Minimize effort
Motion Set Constraint
[TRO 2025 (WIP)]
Get to the goal
Minimize effort
Multi-Horizon Optimization
Motion Set Constraint
[TRO 2025 (WIP)]
Trajectory Optimization: Step 1
Roll out an input trajectory guess to obtain an initial trajectory.
[TRO 2025 (WIP)]
Trajectory Optimization: Step 2
Create a feasible set around each point to obtain a local dynamics model around the trajectory
[TRO 2025 (WIP)]
Trajectory Optimization: Step 3
Use our subproblem to solve for a new input trajectory
[TRO 2025 (WIP)]
Trajectory Optimization: Iteration
Rollout the new initial input guess
[TRO 2025 (WIP)]
Model Predictive Control (MPC)
Plan a trajectory towards the goal in an open-loop manner
[TRO 2025 (WIP)]
Model Predictive Control (MPC)
Execute the first action.
Due to model mismatch, there will be differences in where we end up.
[TRO 2025 (WIP)]
Model Predictive Control (MPC)
Replan from the observed state,
execute the first action,
and repeat.
[TRO 2025 (WIP)]
MPC Rollouts
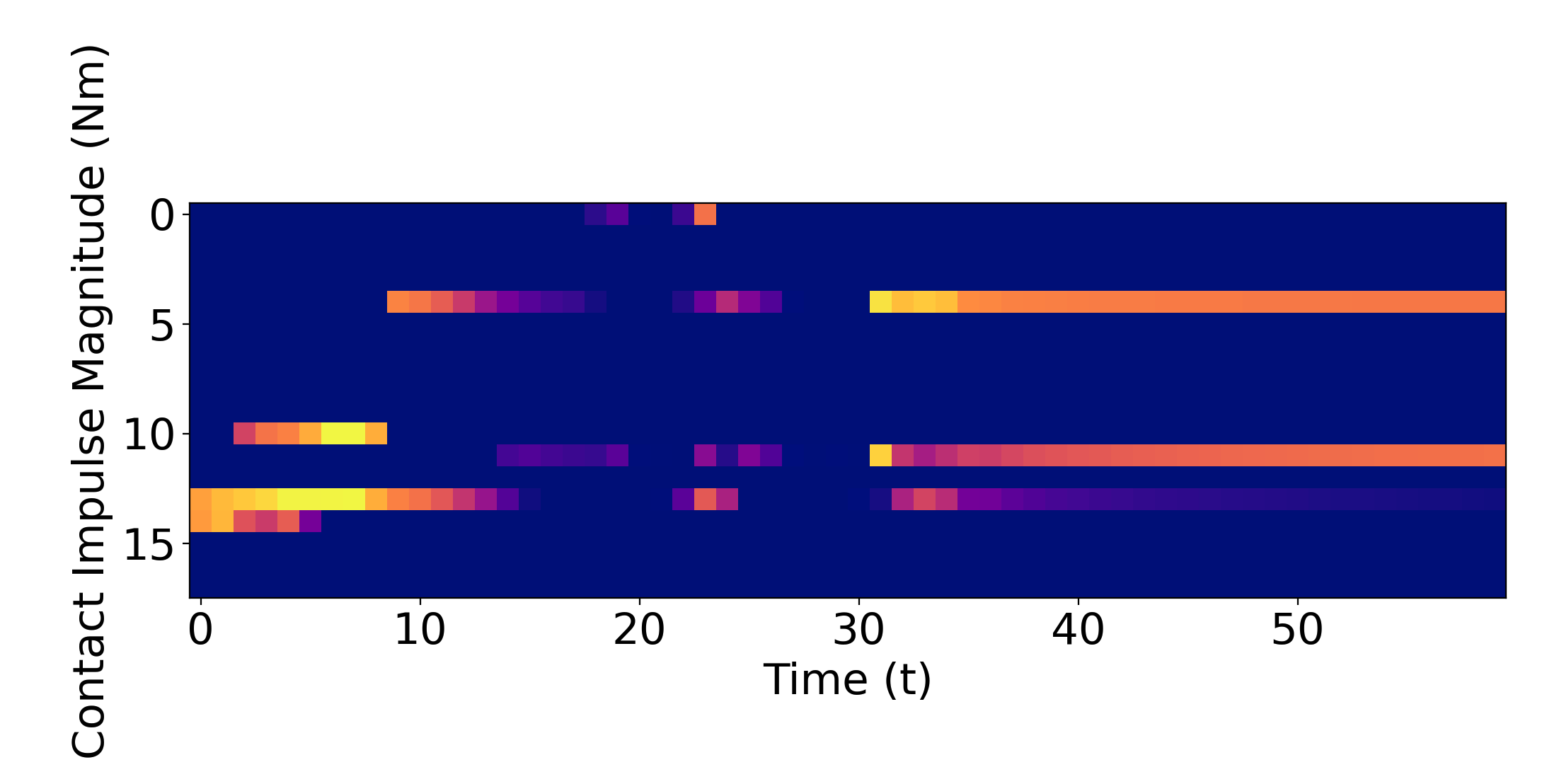

Able to stabilize to plan to the goal in a contact-rich manner
[TRO 2025 (WIP)]
MPC Rollouts
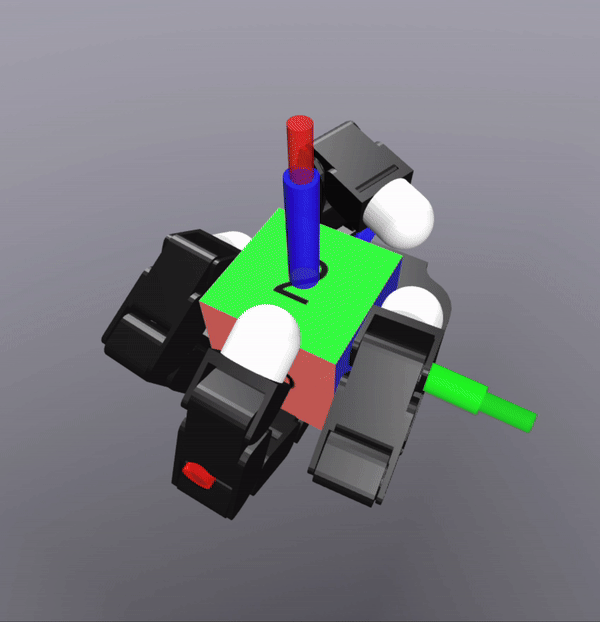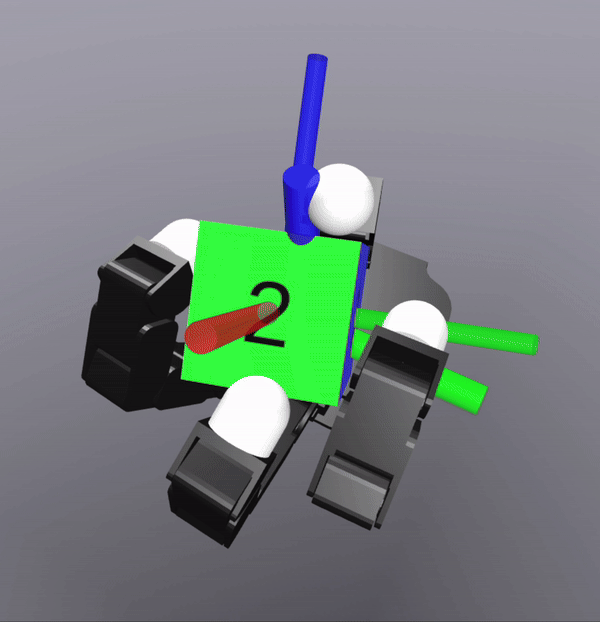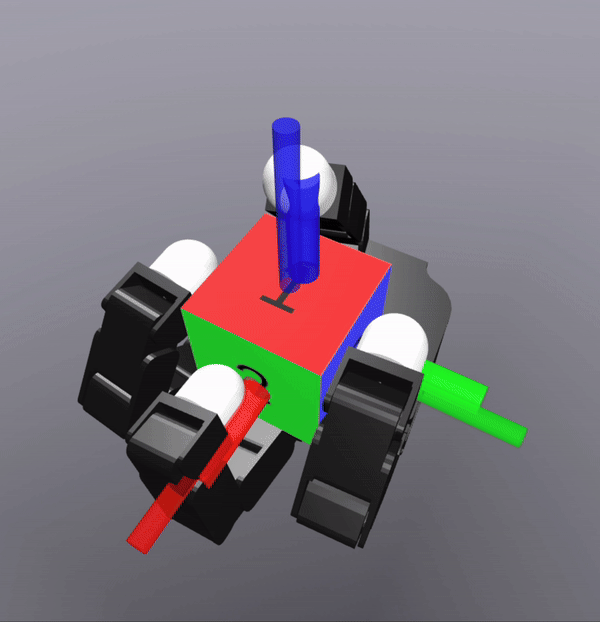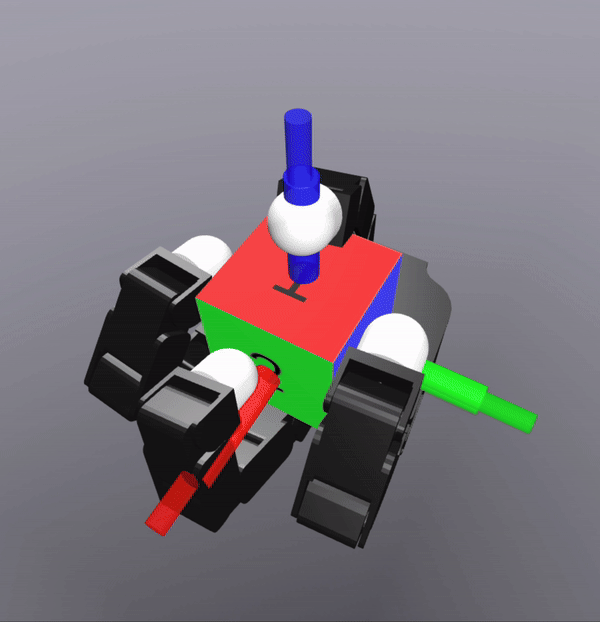


The controller also successfully scales to the complexity of dexterous hands
[TRO 2025 (WIP)]
Experiment Results


Hardware (50 runs)
Drake (1000 runs)
1.37 deg / 1.29cm
2.81 deg / 2.2cm
14.32 deg
16.04 deg
28cm
[TRO 2025 (WIP)]
Is the friction cone constraint necessary?
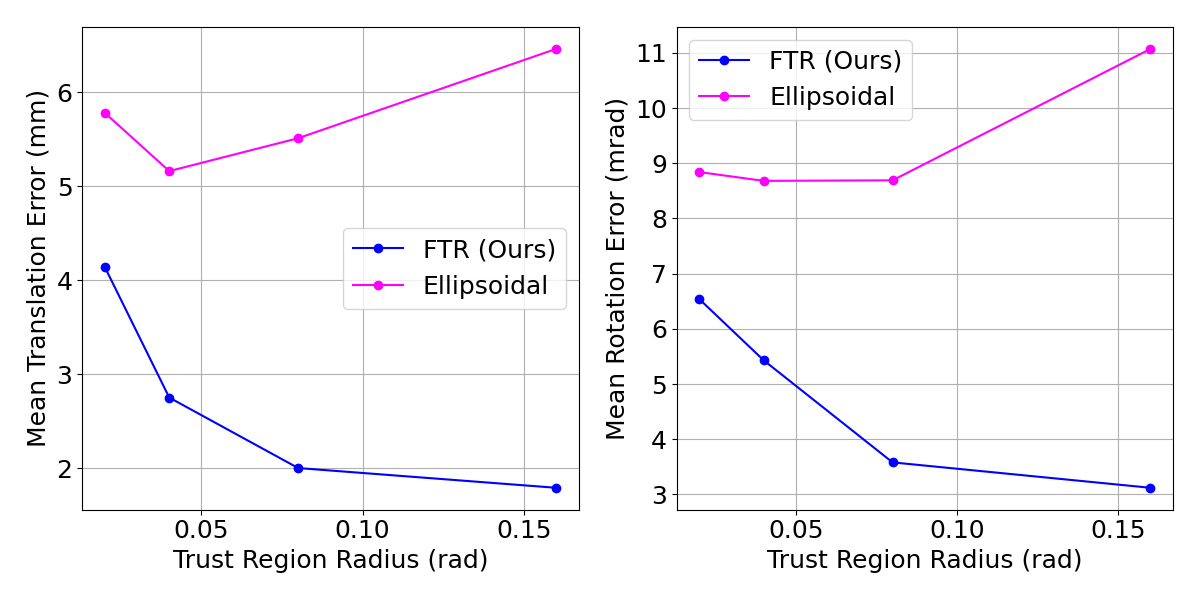
[TRO 2025 (WIP)]
[TRO 2023, TRO 2025]
Part 2. Local Planning for Contact-Rich Manipulation
What is a good local model of contact dynamics?
How do we enable local gradient-based planning?




Contact
Scalability
Efficiency
Global Scope
[TRO 2023, TRO 2025 (WIP)]
[TRO 2023, TRO 2025]
Part 3. Global Planning for Contact-Rich Manipulation
Part 2. Local Planning for Contact-Rich Manipulation
Part 1. Contact Mode Abstraction via Smoothing
Introduction



[TRO 2023, TRO 2025]
Part 3. Global Planning for Contact-Rich Manipulation
What are fundamental limitations of local control?
How can we tackle difficult exploration problems?
How do we enable global planning capabilities?
[TRO 2023, TRO 2025 (WIP)]
Reduction to Motion Planning over Smooth Systems

Smoothing lets us...
- Abstract contact modes
- Gets rid of discreteness coming from granular contact modes.
Contact-Rich Manipulation
Motion Planning over Smooth Systems
The Exploration Problem
The Exploration Problem
The Exploration Problem


How do we push in this direction?
How do we push in this direction?

The Exploration Problem


How do we push in this direction?
How do we push in this direction?

The Exploration Problem
The Exploration Problem

How do I know that I need to open my finger to grasp the box?
[TRO 2023, TRO 2025]
Part 3. Global Planning for Contact-Rich Manipulation
What are fundamental limitations of local control?
How can we tackle difficult exploration problems?
How do we enable global planning capabilities?


[TRO 2023, TRO 2025 (WIP)]
The Exploration Problem

Because I have seen that this state is useful!
Local Control


Local Search for Open-Loop Actions
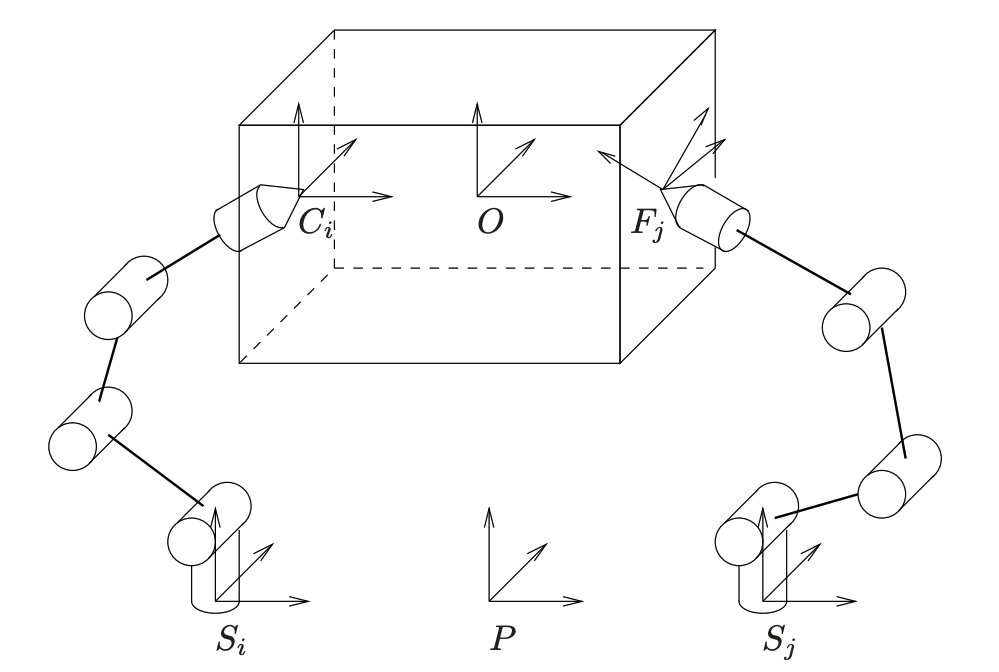
The Robot Relocation Problem



Global Search for Initial Configurations
Local Search for Open-Loop Actions
Where should I place my robot?
The Robot Relocation Problem
Previous Contributions
Grasp Synthesis
Goal-Oriented Grasp Synthesis
Grasp Synthesis

[Venkatesh, Bianchini et al., 2024]

[Ferrari & Canny, 1992]

[Dai et al., 2012]

[Han, Trinkle, Li, 1992]

[Li et al, 2023]

[Fang et al., 2022]
Finding the right cost
High Cost

Finding the right cost
Low Cost

Utilizing the MPC Cost
Our Local Controller
How well does the policy perform when we run local MPC?

Get to the goal
Minimize effort
Motion Set Constraint
[TRO 2025 (WIP)]
Utilizing the MPC Cost
Our Local Controller
How well does the policy perform when we run local MPC?

Get to the goal
Minimize effort
Motion Set Constraint
Efficient, Contact-Scalable MPC allows fast online computation of cost.

[TRO 2025 (WIP)]
The Actuator Relocation Problem
Where should I place my actuators?
Global Search for Initial Configurations
To a place where I can perform local control well
[TRO 2025 (WIP)]
The Robot Relocation Problem
Choose best initial robot configuration for MPC
Non-penetration constraints
[TRO 2025 (WIP)]
The Actuator Relocation Problem
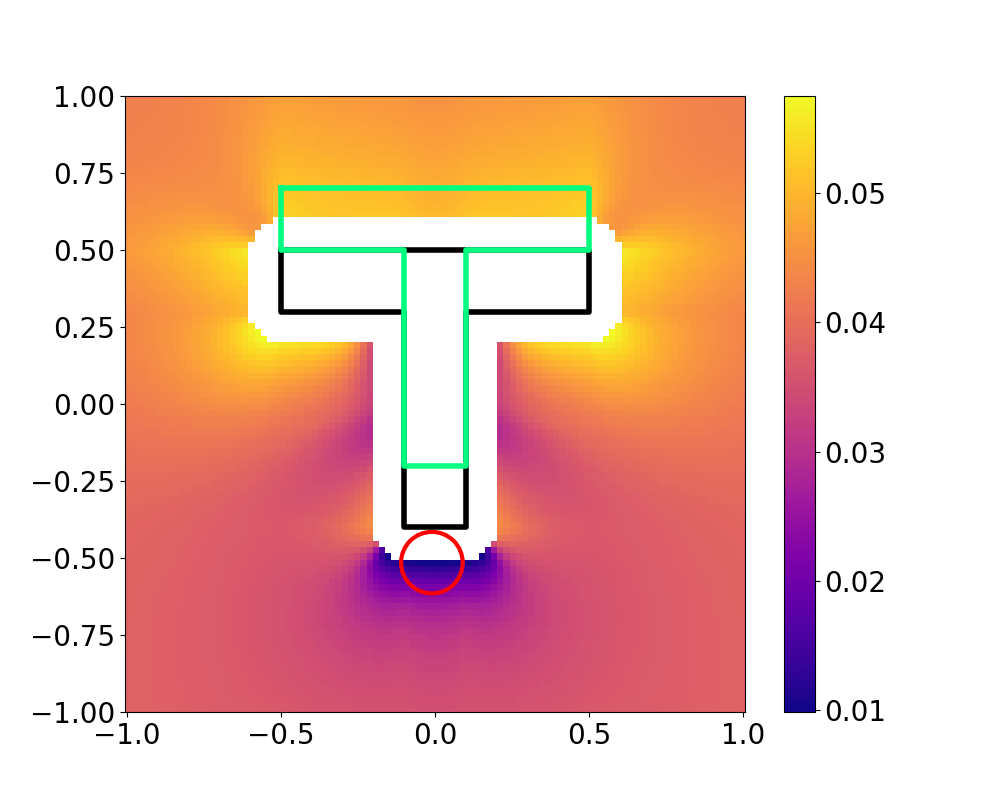
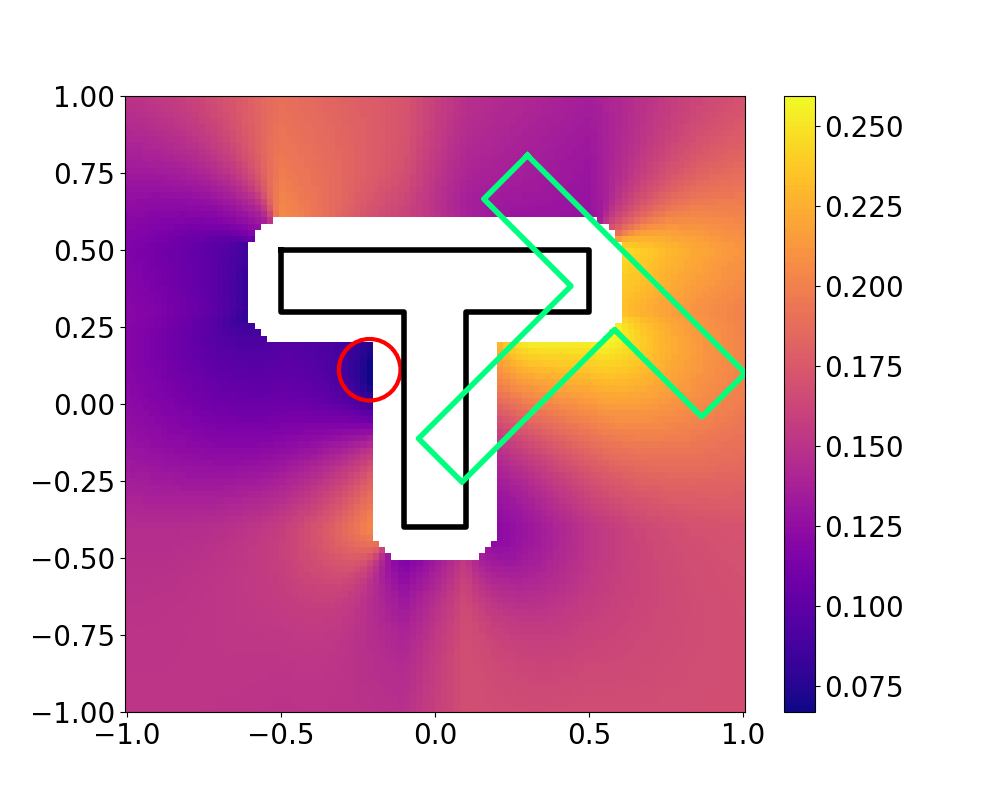
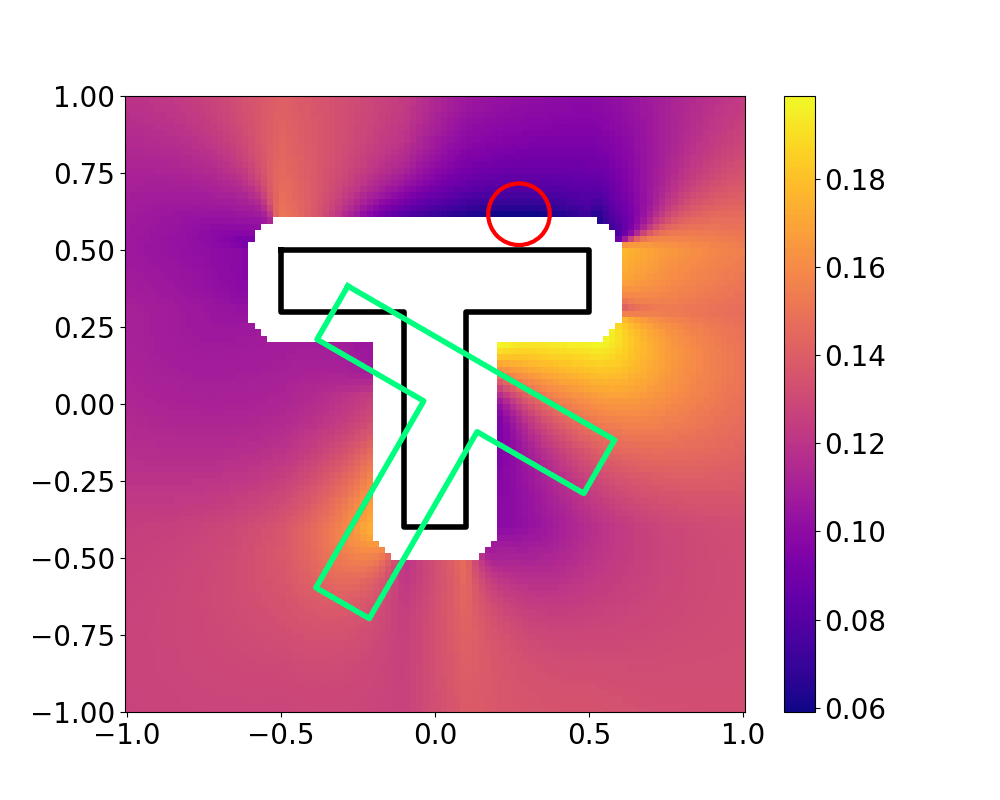
Landscape is much more complex,
sampling-based global optimization is necessary.
[TRO 2025 (WIP)]
Robustness Considerations
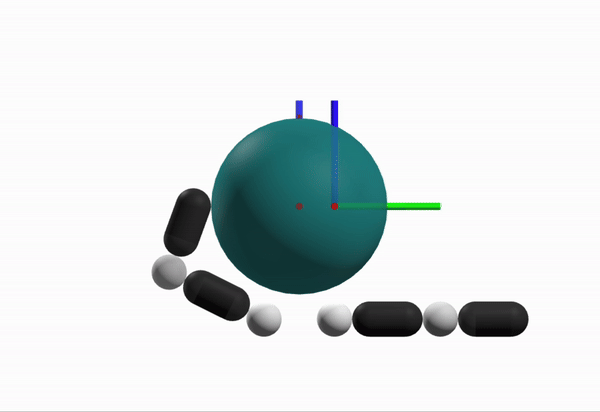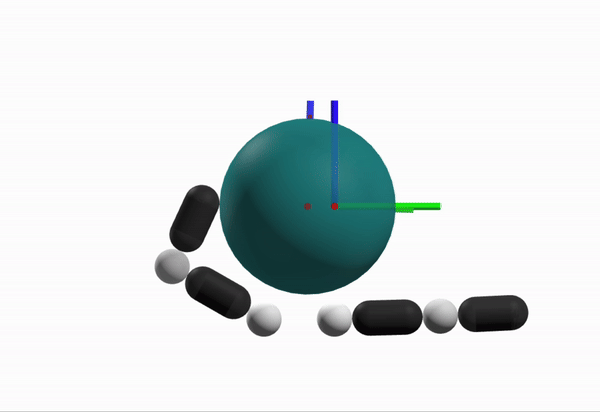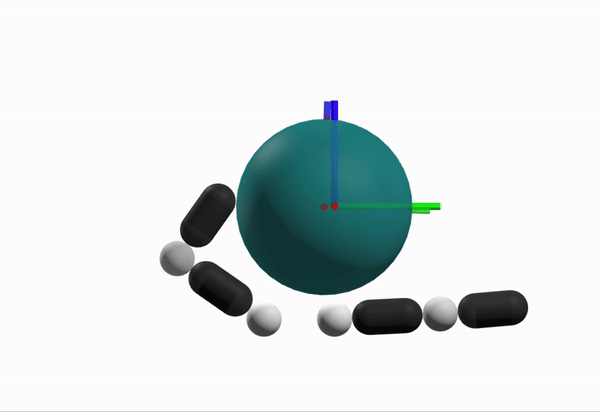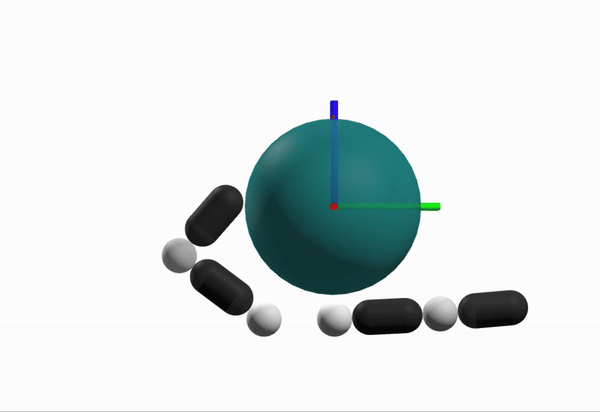
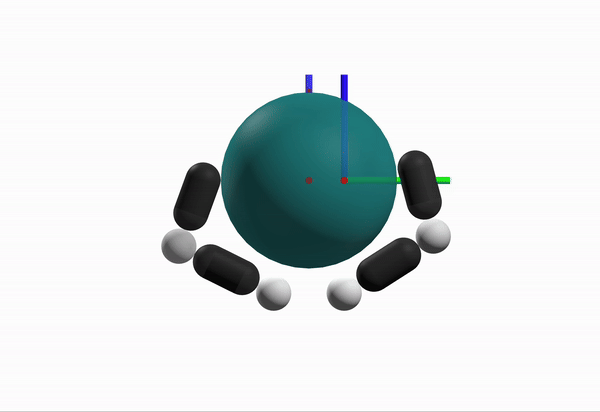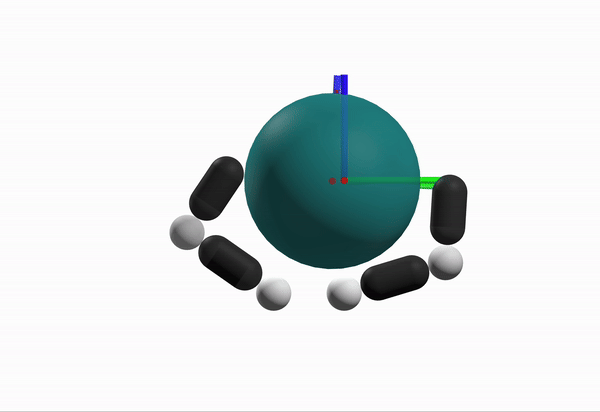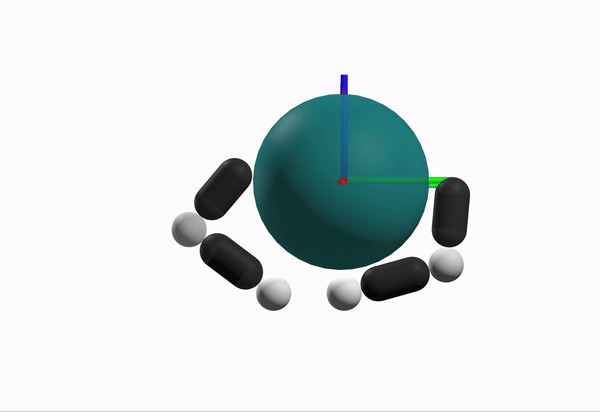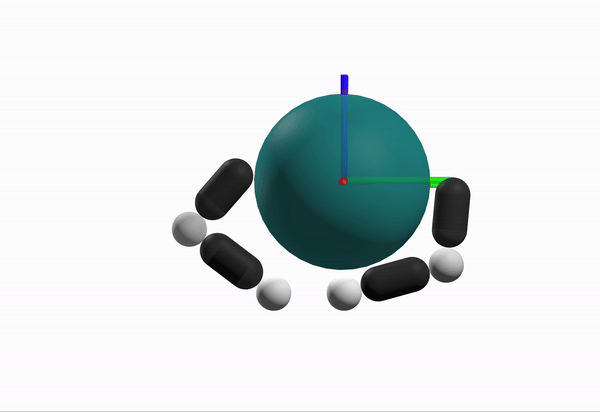
What is a better configuration to start from?
[TRO 2025 (WIP)]
Robustness Considerations

[TRO 2025 (WIP)]
Robustness Considerations

[TRO 2025 (WIP)]
Robustness Considerations

[TRO 2025 (WIP)]
Robustness Considerations

[TRO 2025 (WIP)]
Robustness Considerations

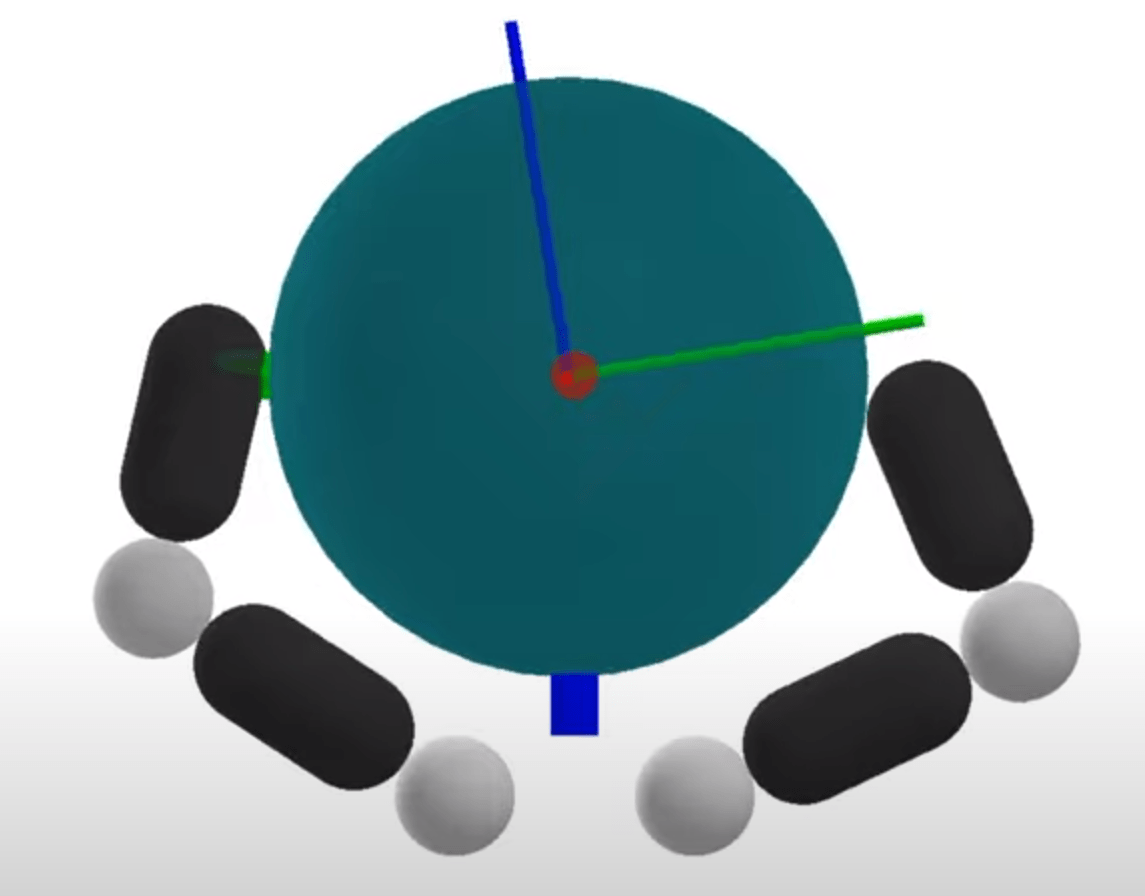
Max Inscribed Sphere within Motion Set
[TRO 2025 (WIP)]
Robustness Considerations




[TRO 2025 (WIP)]
Regularizing with Robustness

[Dai et al., 2012]

[Li et al, 2023]

[Venkatesh, Bianchini et al., 2024]
Be Robust
Be strategic for the task
No Penetration
[TRO 2025 (WIP)]
Grasp Synthesis Procedure
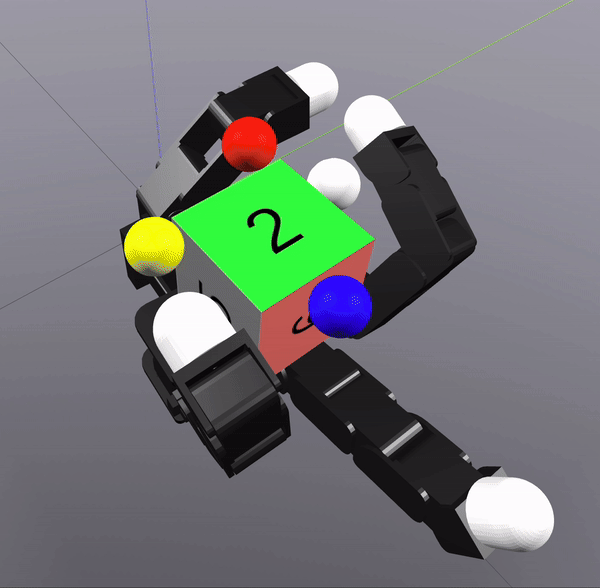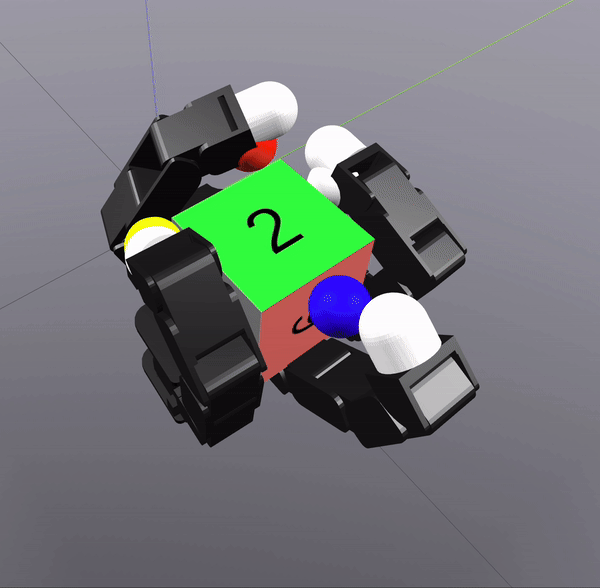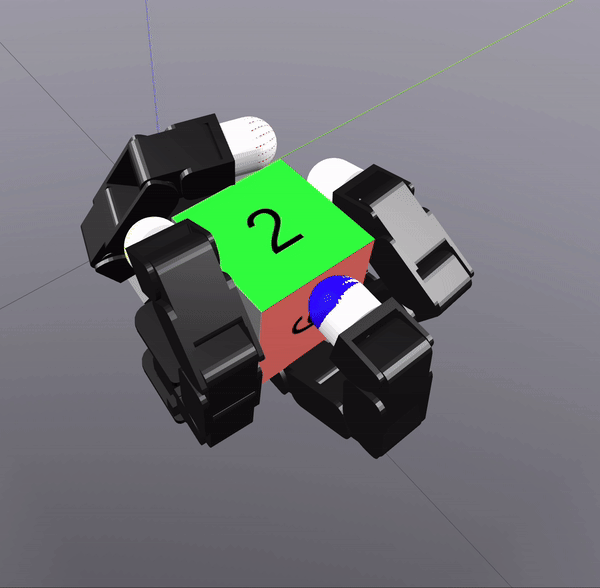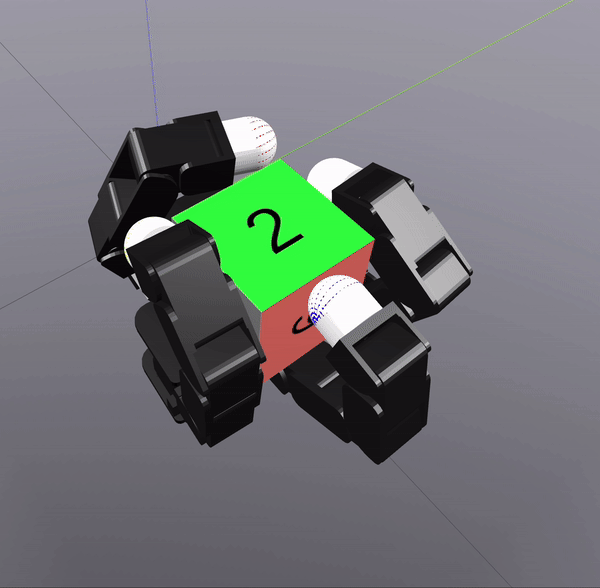

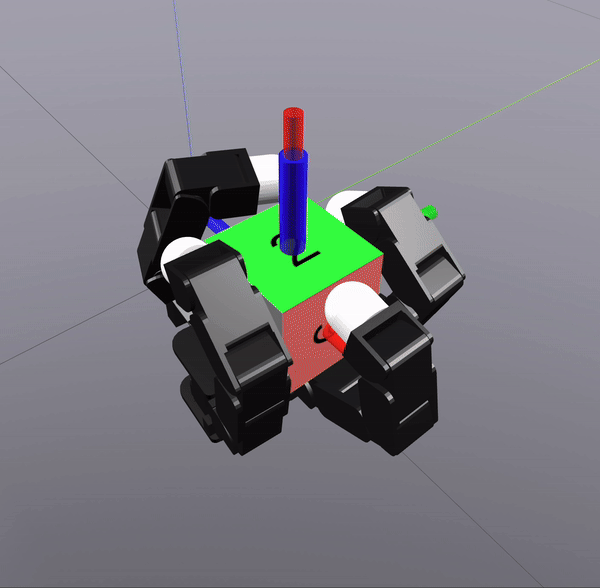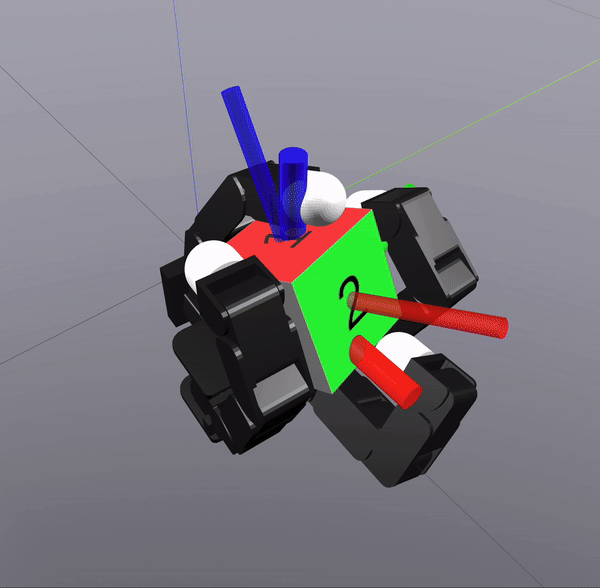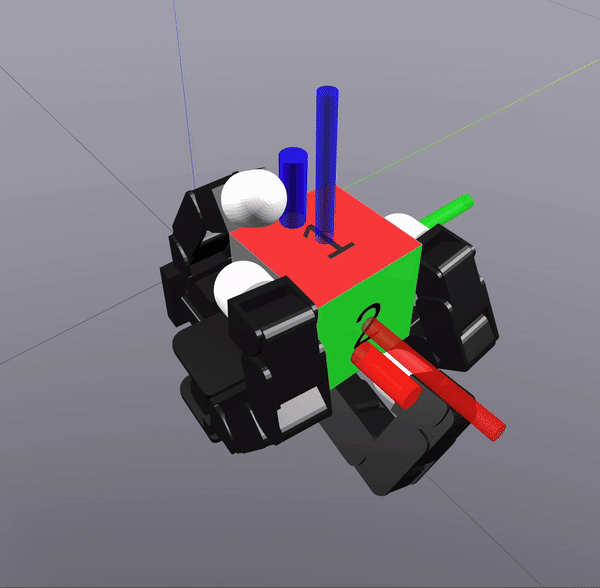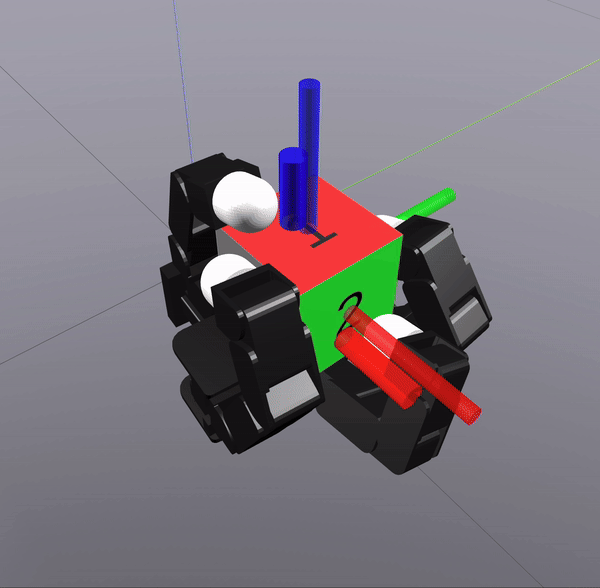
Sampling-Based Search on
Reduced-Order System
Differential Inverse Kinematics to find Hand Configuration
Verification with MPC rollouts
[TRO 2025 (WIP)]
Grasp Synthesis Results



Pitch + 90 degrees
Yaw + 45 degrees
Pitch - 90 degrees
[TRO 2025 (WIP)]
[TRO 2023, TRO 2025]
Part 3. Global Planning for Contact-Rich Manipulation
What are fundamental limitations of local control?
How can we tackle difficult exploration problems?
How do we enable global planning capabilities?



[TRO 2023, TRO 2025 (WIP)]
Sampling-Based Motion Planning (SBMP)

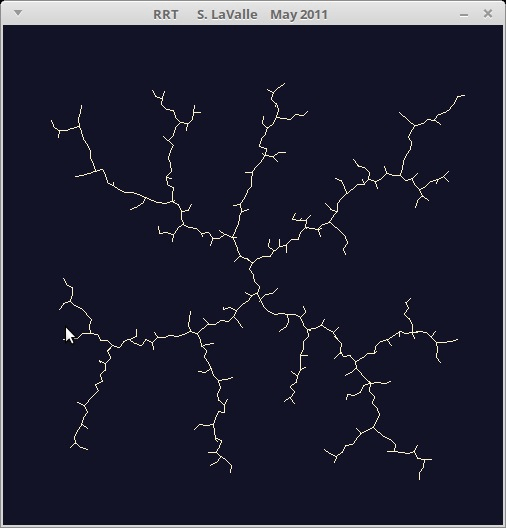
[Kavraki, 1996]
[LaValle, 1998]
Probabilistic Roadmap (PRM)
Rapidly Exploring Random Tree (RRT)
Previous Contributions

[Cheng et al., 2022]

[Cheng et al., 2024]



[Wu et al., 2020]
[Chen et al., 2021]


[Toussaint, 2015]
[Zhu et al., 2022]
[Khandate et al., 2024]
Grasp Synthesis + MPC
Object Configuration Space
[TRO 2025 (WIP)]
Grasp Synthesis + MPC
Object Configuration Space
[TRO 2025 (WIP)]
Grasp Synthesis + MPC
Object Configuration Space
MPC
[TRO 2025 (WIP)]
Grasp Synthesis + MPC
MPC

[TRO 2025 (WIP)]
Grasp Synthesis + MPC
MPC
MPC

[TRO 2025 (WIP)]

Grasp Synthesis + MPC
MPC
MPC


How do I chain these trajectories in the full configuration space?
[TRO 2025 (WIP)]
Grasp Synthesis + MPC
MPC
MPC

Regrasp
(Collision-Free Motion Planning)

[TRO 2025 (WIP)]
Chaining Local Actions
[TRO 2025 (WIP)]
Roadmap Approach to Manipulation
Offline, build a roadmap of object configuration and keep collection of nominal plans as edges
[TRO 2025 (WIP)]
Roadmap Approach to Manipulation
Roadmap Approach to Manipulation
When getting a new goal that is not in the roadmap, try to connect from nearest node.
[TRO 2025 (WIP)]
[TRO 2023, TRO 2025]
Part 3. Global Planning for Contact-Rich Manipulation
How do we enable global planning capabilities?
[TRO 2023, TRO 2025 (WIP)]
The real discreteness comes from motion planning, not contact modes.

When we abstract contact modes with smoothing, SBMP can be highly efficient.

Difficult exploration problems can be alleviated with offline search for initial conditions.

[TRO 2023, TRO 2025]
Part 3. Global Planning for Contact-Rich Manipulation
Part 2. Local Planning for Contact-Rich Manipulation
Part 1. Contact Mode Abstraction via Smoothing
Introduction



Summary
Our Method


Contact Scalability
Efficiency
Global Planning

60 hours, 8 NVidia A100 GPUs
5 minutes, 1 Macbook CPU
















































Thank You

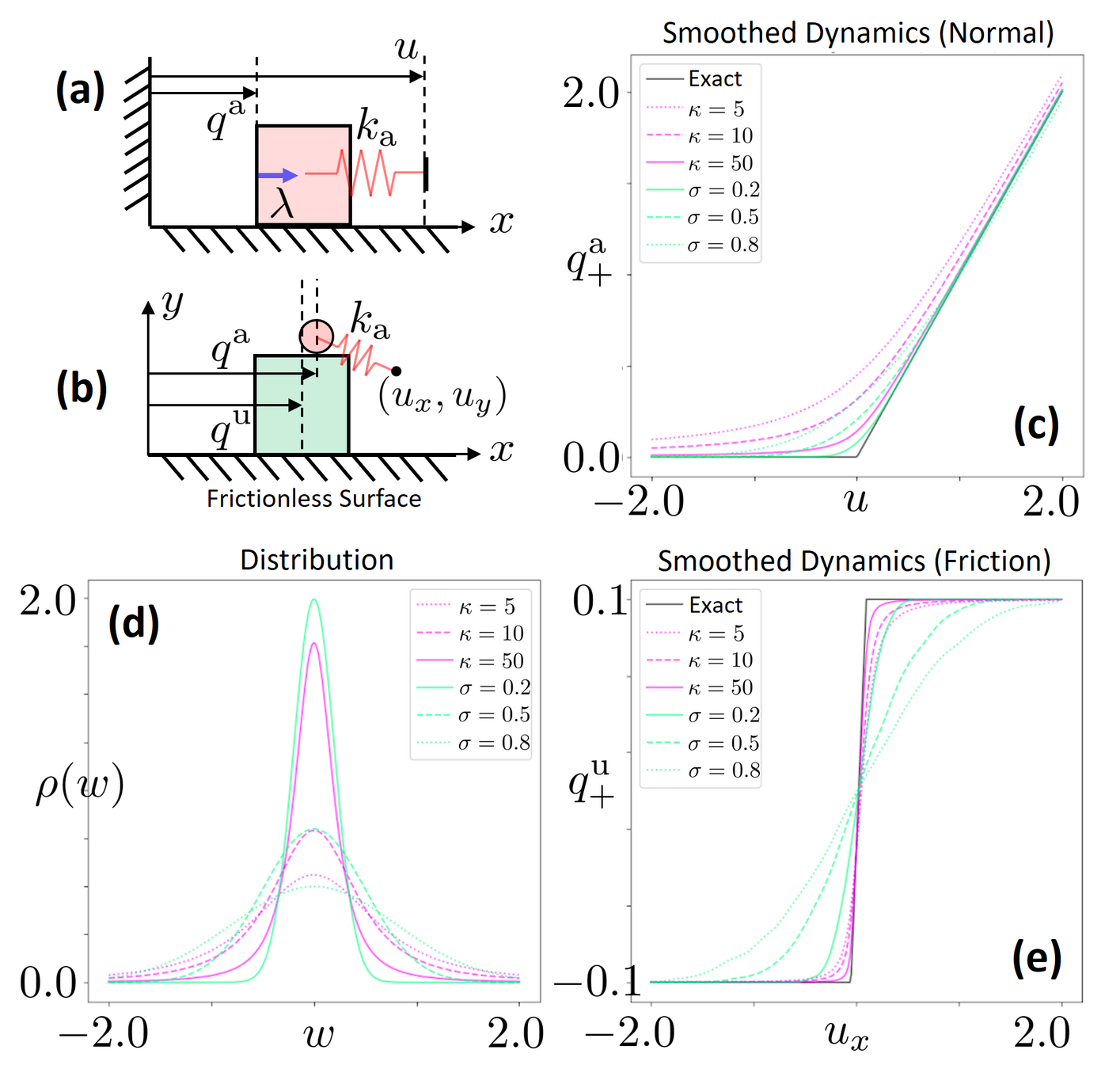
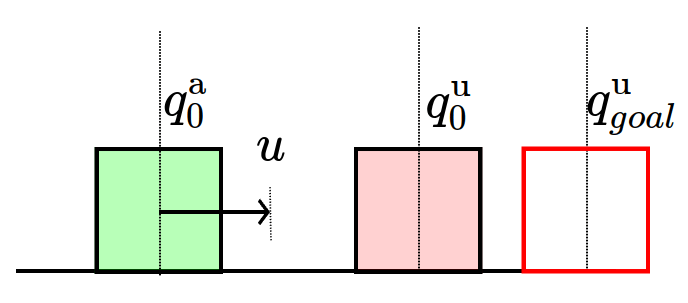
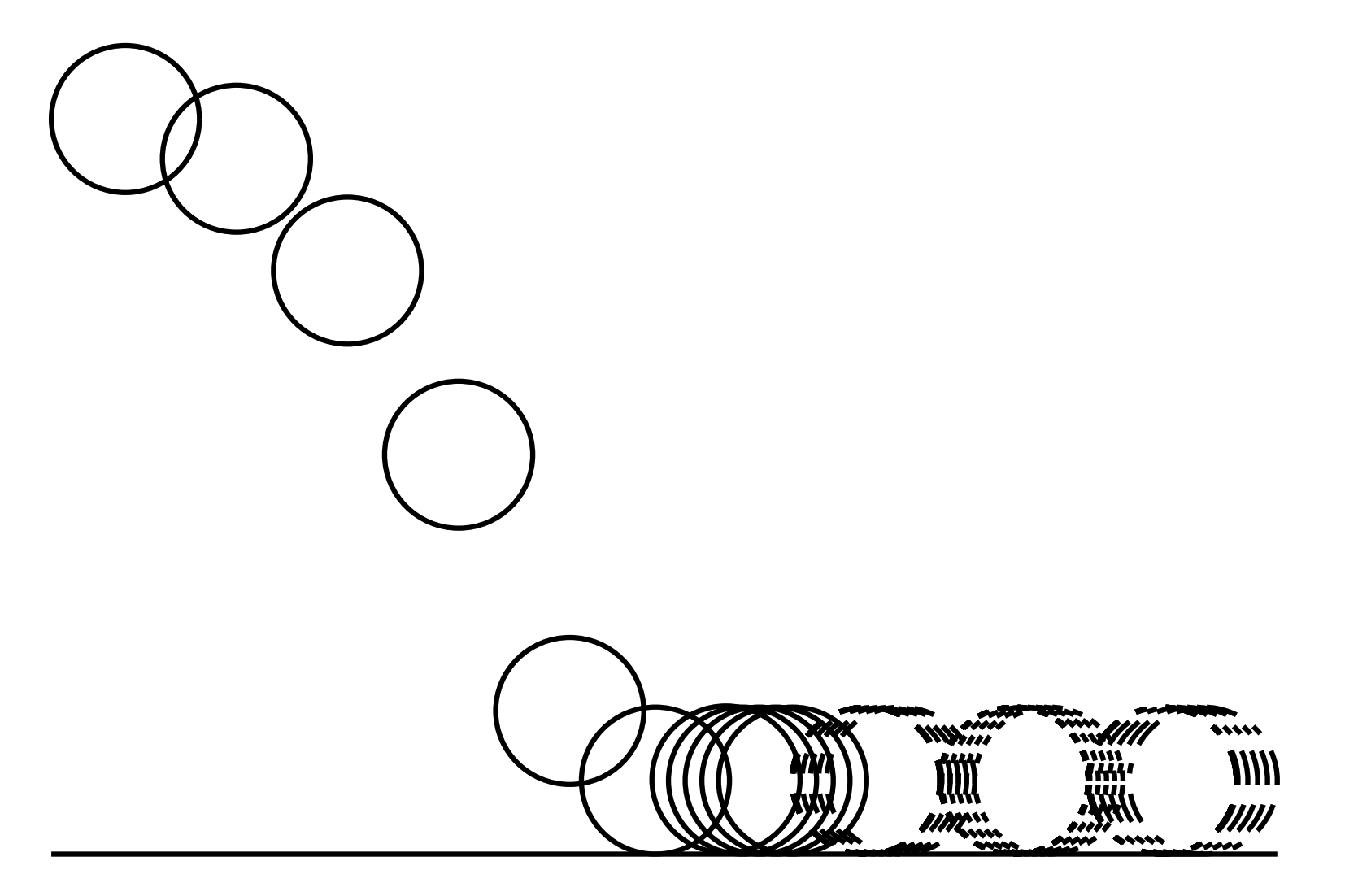
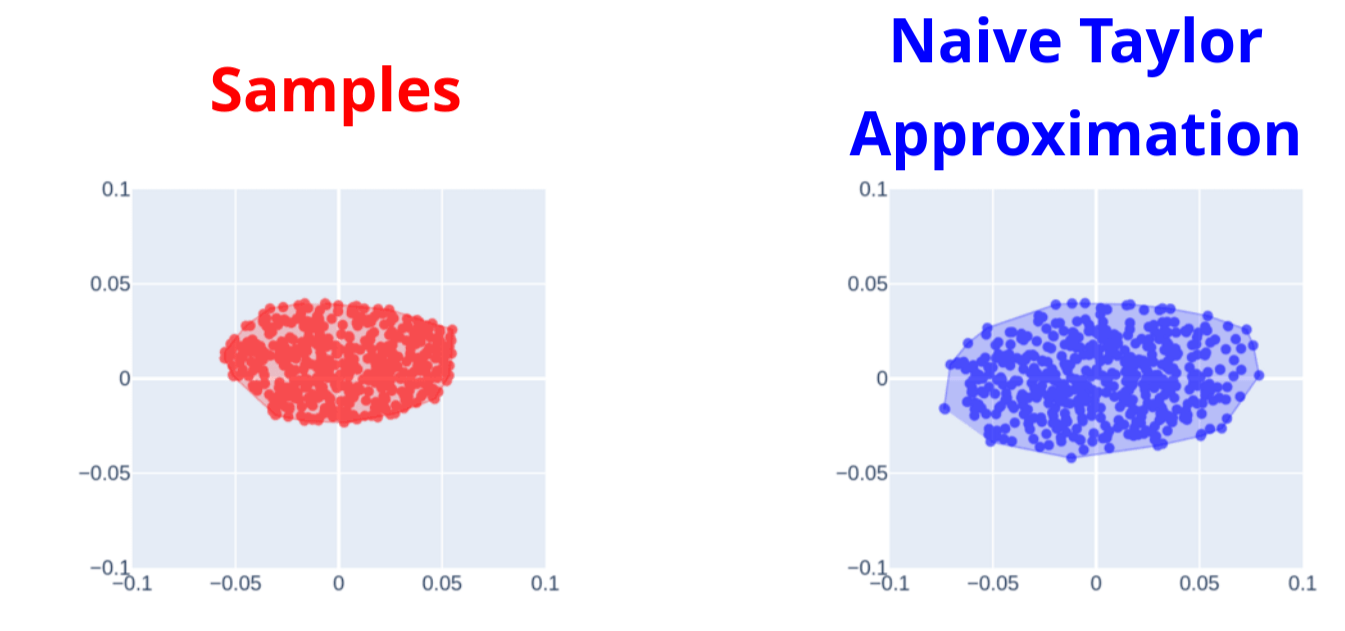
Attempt 1. Penalty Method

- No force when not in contact
- Spring-damper behavior when in contact

- No force when not in contact
- Spring-damper behavior when in contact
Attempt 1. Penalty Method

- No force when not in contact
- Spring-damper behavior when in contact
Attempt 1. Penalty Method
Attempt 1. Penalty Method

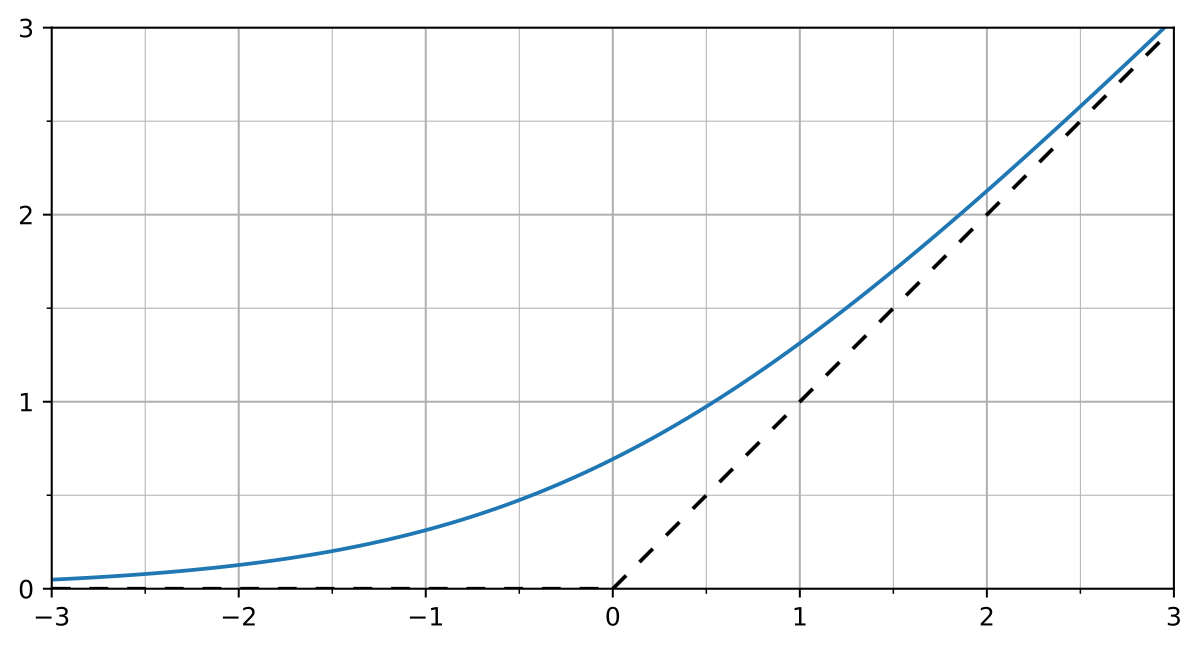
Attempt 1. Penalty Method


Can take gradients efficiently
Abstracts contact without Monte-Carlo



Penalty Method & Force-Level Relaxation
Penalty-Based Simulation
Force-Level Relaxation

[Geilinger et al., 2020]

[Hunt & Crossley, 1975]

[Castro et al., 2020]


[Huang et al., 2021]
[Turpin et al., 2023]

[Drumwright, 2008]

[Suh & Wang, 2019]
Cons of the Penalty Method
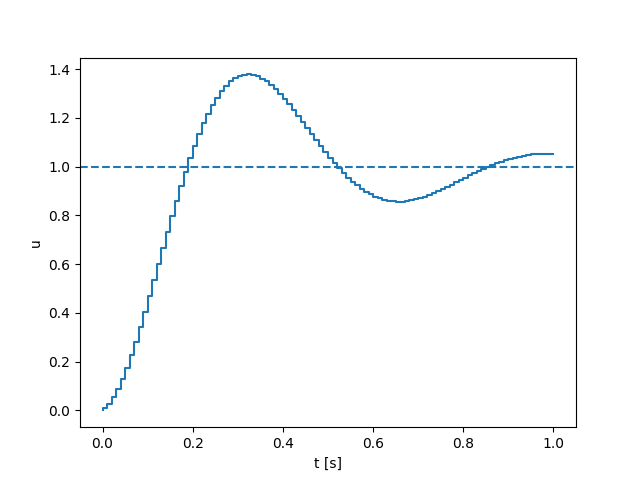
Spring-damper modeling


Realistic behavior requires stiff springs

Gradients capture transient behavior
Cons of the Penalty Method
Good gradients require good models

Spring-damper modeling

Robustness Considerations

[Ferrari & Canny, 1992]

[TRO 2025 (WIP)]
Robustness Considerations

[Ferrari & Canny, 1992]

[TRO 2025 (WIP)]
Robustness Considerations

[Ferrari & Canny, 1992]

[TRO 2025 (WIP)]
Robustness Considerations

[Ferrari & Canny, 1992]

[TRO 2025 (WIP)]
Robustness Considerations

[Ferrari & Canny, 1992]

[TRO 2025 (WIP)]
Robustness Considerations

[Ferrari & Canny, 1992]

[TRO 2025 (WIP)]
Optimal Control on a Local Model
Get to the goal
Minimize effort
Dynamics



Local Model over the Dynamics
Dynamics




Local Model over the Dynamics
Dynamics




Local Model over the Dynamics
Dynamics




?
Local Model over the Dynamics
Linearized Dynamics




Local Model over the Dynamics
Terry Suh PhD Thesis Defense
By Terry Suh
Terry Suh PhD Thesis Defense
- 715



