Videos and data
Goal: model
Main lines of the model
- 2 groups
heading to the food
heading to the nest
g_i = -1
g_i = 1
- agents \(i\) with position \(X_i \in \mathbb{R}^2\) and velocity \(V_i \in \mathbb{R}^2\)
V_i
X_i
\times
- Model of evolution :
\dot{X}_i = V_i \\
\dot{V}_i = \textcolor{blue}{F_{\text{self-prop}}} + \textcolor{red}{F_{\text{drive}}}
+ \textcolor{orange}{F_{\text{interact}}}
\; \tiny{(+ \textcolor{brown}{F_{\text{walls}}})}
\dot{X}_i = V_i \\
\dot{V}_i = \sum F
- Visual field \(\mathcal{V}_i\)
+
\Theta_i
\mathcal{V}_i = \{j,\ell\}
Visual field \(\mathcal{V}_i\)
i
\Theta_i = \frac{V_i}{|V_i|}
orientation
j
k
\ell
m
Forces
\dot{X}_i = V_i \\
\dot{V}_i = \textcolor{blue}{F_{\text{self-prop}}} + \textcolor{red}{F_{\text{drive}}} + \textcolor{orange}{F_{\text{interact}}}
\textcolor{blue}{F_{\text{self-prop}}} = \nu \, (\xi -| V_i|) \Theta_i
1. Self-propulsion
\textcolor{orange}{F_{\text{interact}}} = \textcolor{orange}{F_{\text{same group}}} + \textcolor{orange}{F_{\text{other group}}}
\textcolor{red}{F_{\text{drive}}} = c_{\text{drive}} \, \begin{pmatrix} g_i \\ 0 \end{pmatrix}
\(\nu > 0\) strength of the force
\(\xi > 0\) target velocity magnitude
3. Interaction
2. Drive
drives to the right if \(g_i = 1\)
drives to the left if \(g_i = -1\)
controls the velocity magnitude
drives towards the objective
deals with the other agents
\Theta_i = \frac{V_i}{|V_i|}
Forces
\dot{X}_i = V_i \\
\dot{V}_i = \textcolor{blue}{F_{\text{self-prop}}} + \textcolor{red}{F_{\text{drive}}} + \textcolor{orange}{F_{\text{interact}}}
\textcolor{blue}{F_{\text{self-prop}}} = \nu \, (\xi -| V_i|) \Theta_i
1. Self-propulsion
\(\nu > 0\) strength of the force
\(\xi > 0\) target velocity magnitude
controls the velocity magnitude
drives towards the objective
deals with the other agents
\Theta_i = \frac{V_i}{|V_i|}
Force self-propulsion
\textcolor{blue}{F_{\text{self-prop}}} = \nu \, (|V_i| - \xi) \Theta_i
The parameters \(\nu\) and \(\xi\) chosen according to the situation:
depends on the visual field \(\mathcal{V}_i\)
1. No obstacles
\nu = \nu_{\text{cruise}} \; \; \scriptsize{(\sim 15)}
\xi = \xi_{\text{cruise}} \; \; \scriptsize{(\sim 8)}
2. Head-on contact with another agent
\nu = \nu_{\text{brake}} \; \; \scriptsize{(\sim 100)}
\xi = \xi_{\text{brake}} \; \; \scriptsize{(\sim 0.1)}
\leqslant d_{\text{contact}} \;\scriptsize{(\sim 2.4)}
3. Generic contact with another agent
\nu = \lambda \nu_{\text{brake}} + (1 - \lambda) \nu_{\text{cruise}}
\leqslant d_{\text{contact}}
\xi = \lambda \xi_{\text{brake}} + (1 - \lambda) \xi_{\text{cruise}}
cruising
braking
sliding
\lambda = \left|\Theta_i \cdot \frac{X_j-X_i}{|X_j-X_i|} \right|^{\alpha_{\text{sp}}}
or
Forces
\dot{X}_i = V_i \\
\dot{V}_i = \textcolor{blue}{F_{\text{self-prop}}} + \textcolor{red}{F_{\text{drive}}} + \textcolor{orange}{F_{\text{interact}}}
\textcolor{blue}{F_{\text{self-prop}}} = \nu \, (|V_i| - \xi) \Theta_i
1. Self-propulsion
\textcolor{orange}{F_{\text{interact}}} = \textcolor{orange}{F_{\text{same group}}} + \textcolor{orange}{F_{\text{other group}}}
\textcolor{red}{F_{\text{drive}}} = c_{\text{drive}} \, \begin{pmatrix} g_i \\ 0 \end{pmatrix}
\(\nu > 0\) strength of the force
\(\xi > 0\) target velocity magnitude
3. Interaction
2. Drive
drives to the right if \(g_i = 1\)
drives to the left if \(g_i = -1\)
controls the velocity magnitude
drives towards the objective
deals with the other agents
\Theta_i = \frac{V_i}{|V_i|}
Force \(F_{\text{interact}}\)
\textcolor{orange}{F_{\text{interact}}} = \textcolor{orange}{F_{\text{same group}}} + \textcolor{orange}{F_{\text{other group}}}
Depends on the visual field \(\mathcal{V}_i\)
\(\mathrm{I}\). Same group
attraction
repulsion
\(\mathrm{II}\). Other group
attraction
steer (avoid)
1/2
d_{\text{ref},1}
d_{\text{ref},2}
d_{\text{contact}}
nothing
Force \(F_{\text{interact}}\)
\textcolor{orange}{F_{\text{interact}}} = \textcolor{orange}{F_{\text{same group}}} + \textcolor{orange}{F_{\text{other group}}}
Depends on the visual field \(\mathcal{V}_i\)
\(\mathrm{I}\). Same group
\textcolor{orange}{F_{\text{same group}}} = c_{\text{same}} \underset{g_j = g_i}{\sum_{j \in \mathcal{V}_i}}
\left(\frac{d_{\text{ref},1}}{|X_j - X_i|} \right)^{\alpha_{\text{same}}} \; \log \left(\frac{d_{\text{ref},1}}{|X_j - X_i|} \right) \; \frac{X_j - X_i}{|X_j - X_i|}
attraction if
\(|X_j - X_i|> d_{\text{ref}}\)
repulsion if
\(|X_j - X_i|< d_{\text{ref}}\)
\(\mathrm{II}\). Other group
\textcolor{orange}{F_{\text{other group}}} = \underset{g_j \neq g_i}{\sum_{j \in \mathcal{V}_i}}
c_{\text{other}} \, \mathbf{1}_{d_{\text{contact}} < |X_j - X_i| < d_{\text{ref},2}} \, \frac{X_j - X_i}{|X_j - X_i|} \; \; +
\; \; \mathbf{1}_{|X_j - X_i| < d_{\text{contact}}} \, \textcolor{purple}{F_{ij}^{\text{steer}}}
attraction
steer (avoid)
2/2
+
X_i
\Theta_i
+
X_j
\sigma
\sigma^{\perp}_+
\sigma^{\perp}_-
\Theta_j
If \(\Theta_j \cdot \sigma^{\perp}_+ \leq 0 \) :
+
X_i
\Theta_i
+
X_j
\sigma
\sigma^{\perp}_+
\sigma^{\perp}_-
\Theta_j
\sigma^\perp = \sigma^\perp_+
Then
\(\sigma^\perp_+\) chosen such that
\(\Theta_i \cdot \sigma^{\perp}_+ \geq 0\)
If \(\Theta_j \cdot \sigma^{\perp}_+ \geq 0 \) :
\sigma^\perp = \sigma^\perp_-
If \(|\Theta_i \cdot \sigma| \geq |\Theta_j \cdot \sigma|\) then
Else
\sigma^\perp = \sigma^\perp_+
\textcolor{purple}{F_{\text{steer}}} = c_{\text{steer}} \; |\Theta_i \cdot \sigma|^{\alpha_{\text{steer}}} \times \sigma^\perp
Steering force \(F_{\text{steer}}\)
\sigma = \frac{X_j-X_i}{|X_j-X_i|}
Videos
Quantitative properties: velocity magnitudes
Comparison with data
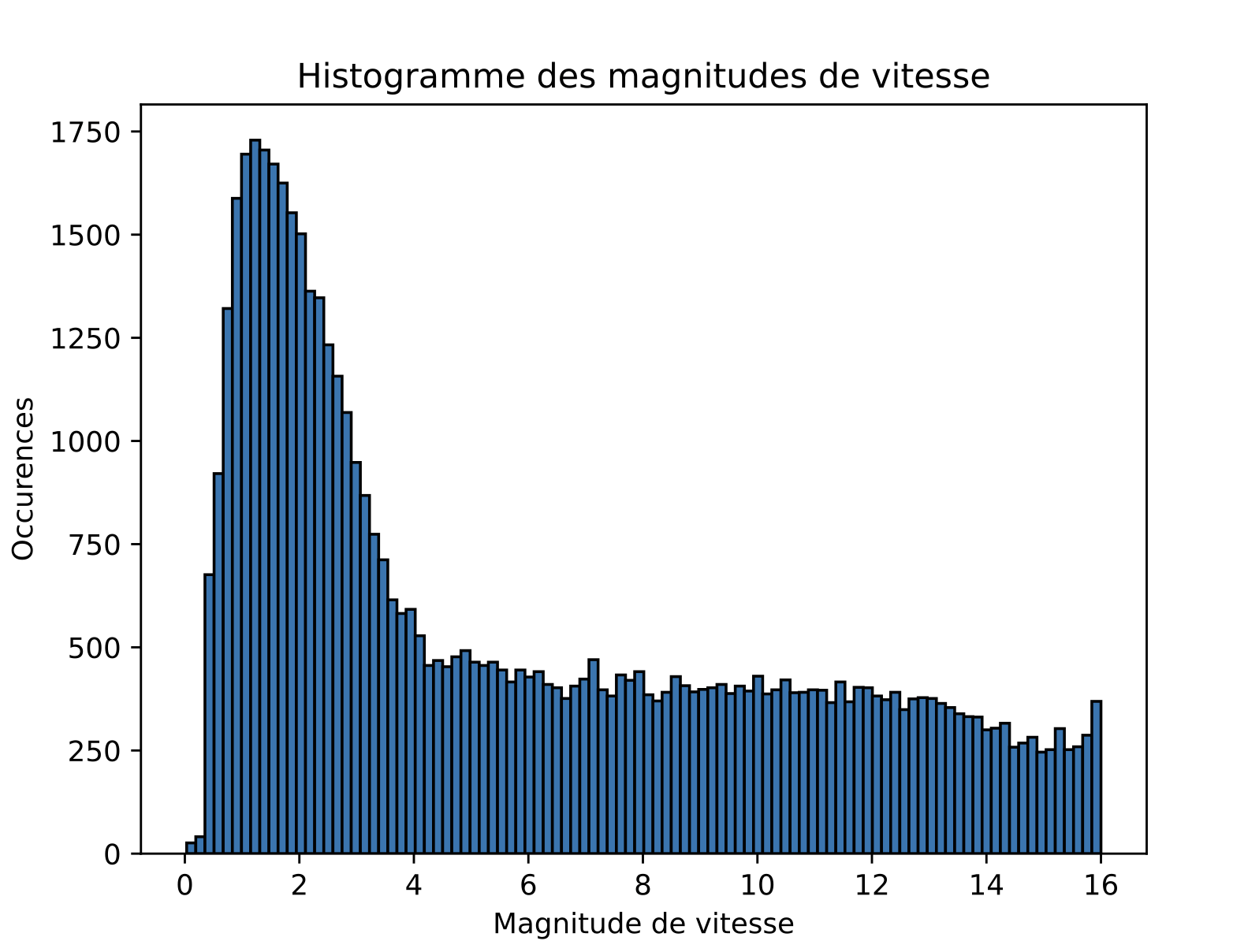
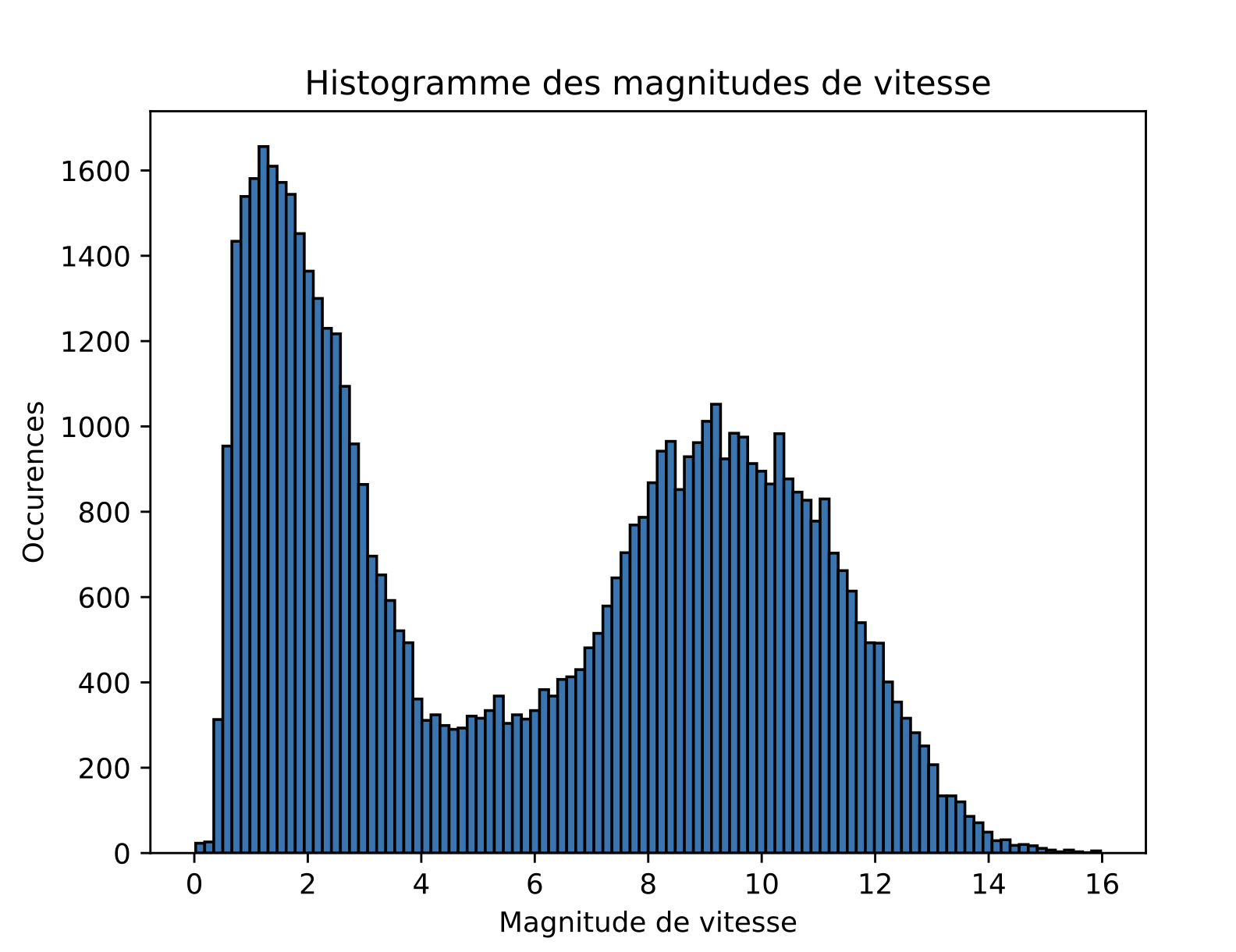
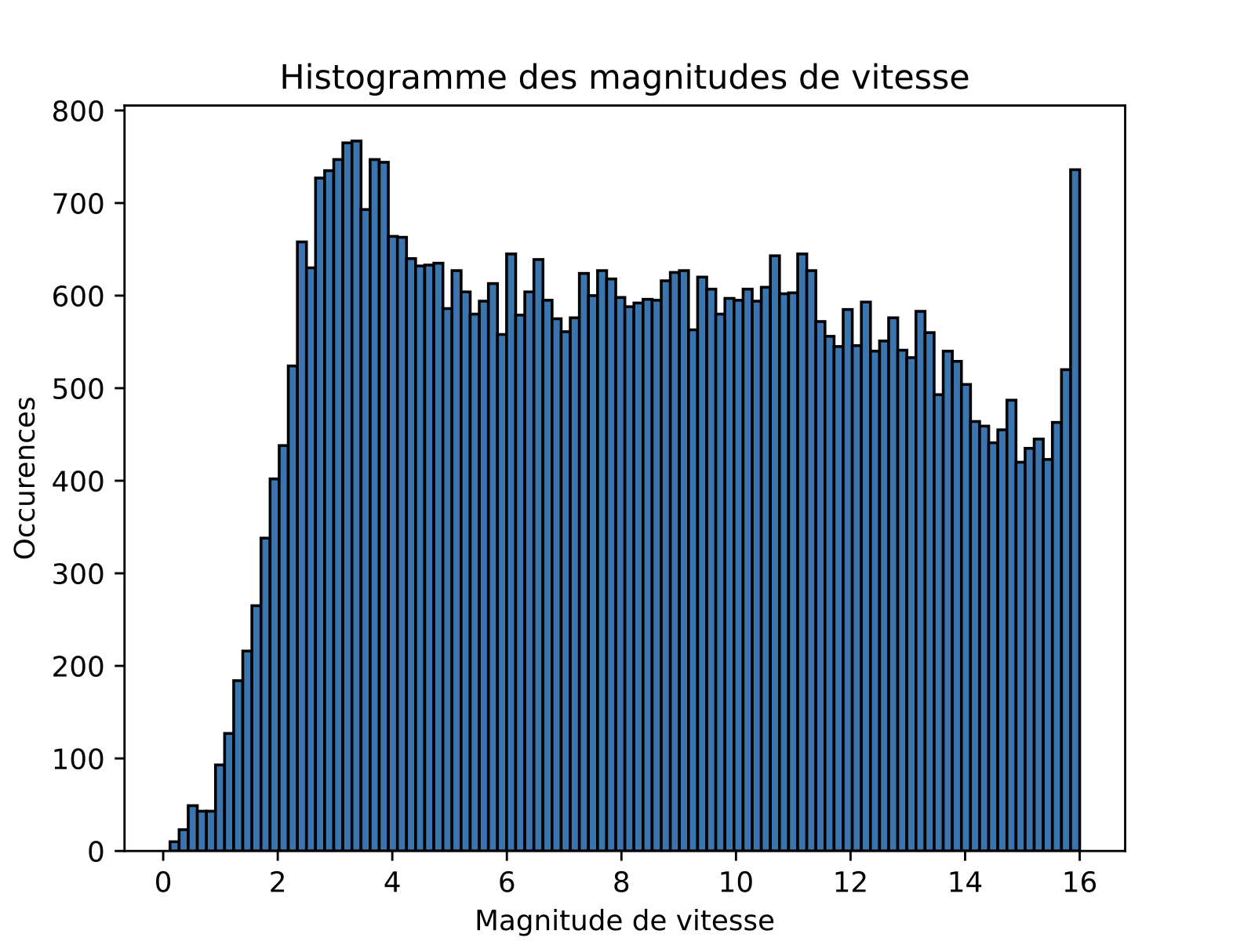
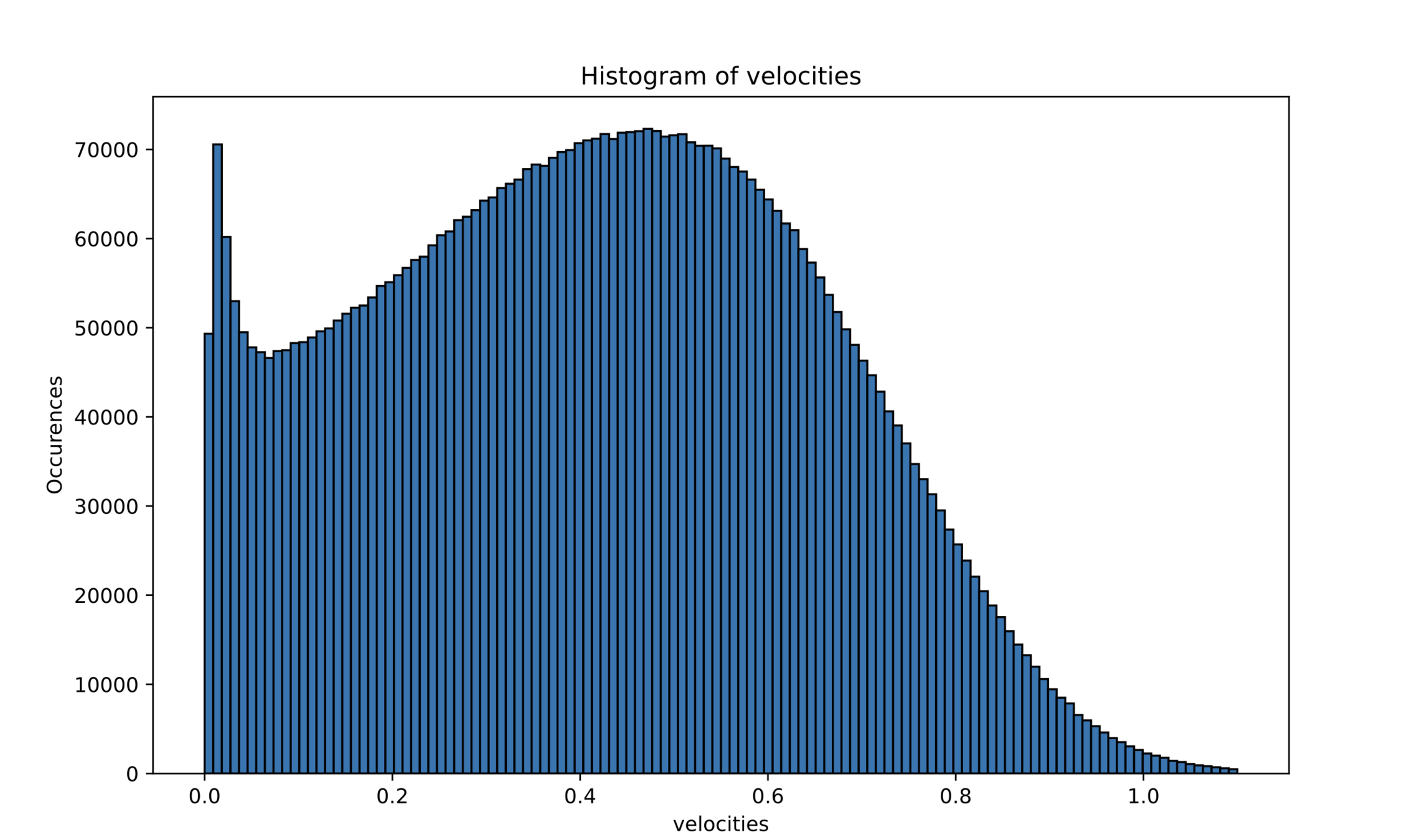
Experimental data:
Simulation:
Sim 2 : smaller \(\nu_{\text{cruise}}\)
Reference simulation
Sim 3 : smaller \(\nu_{\text{cruise}}\) and bigger steering force
Quantitative properties
Two-phase flow?
Simulated flow
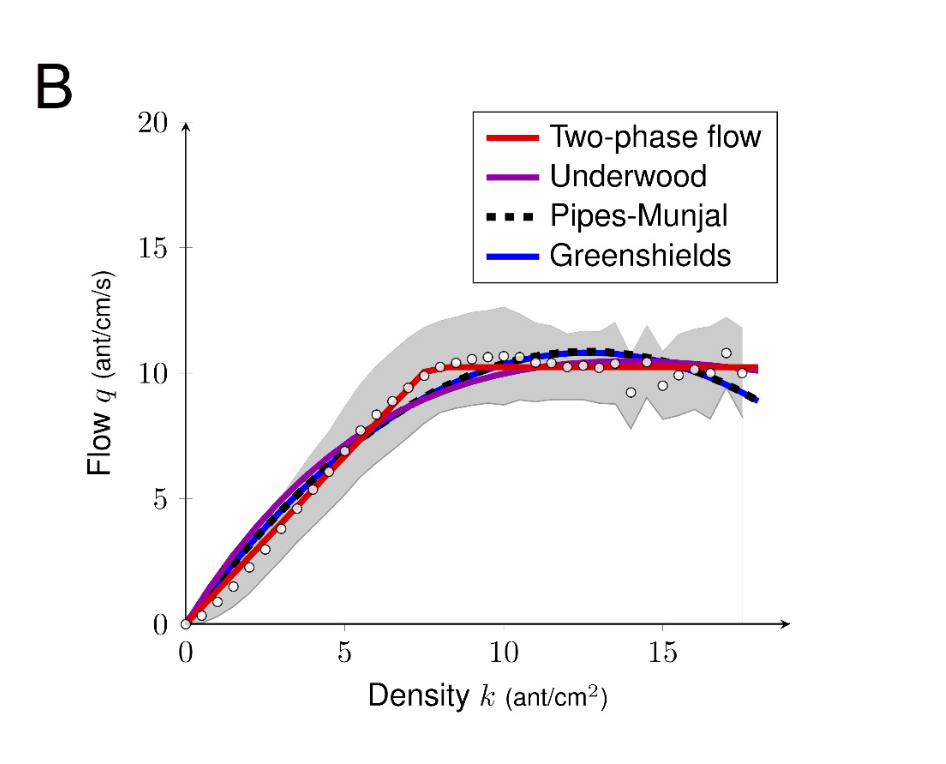
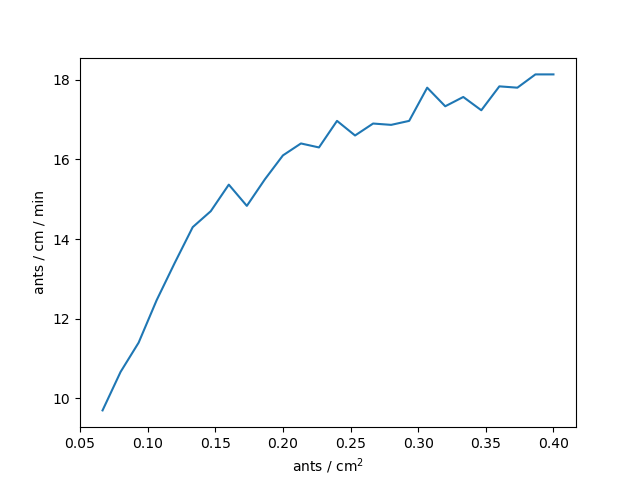
Experimental flow
(Experimental investigation of ant traffic
under crowded conditions)
* En fait la fourmi aime le bord. Suivi de bord "thygmotactisme"
https://fr.wikipedia.org/wiki/Thigmotactisme
Seul à 5, 10 mm, on ne voyait pas trop le bord. A 20 mm, on n'a jamais réussi à avoir un flux suffisant pour occuper tout le pont.
* Elle aime bien l'idée d'une vitesse de croisière. Peu de variabilité individuelle.
* Champ visuel plus large (un peu plus de 180°). (différent du cône de la phéromone qui est plutôt de 60°)
Les fourmis "oscillent" --> osmothropotaxie
* Faible flux: interaction douce, attraction (elles vont l'une vers l'autre, les deux modifient leurs trajectoires) [attraction plutôt 2 fourmis]
Fort traffic: interaction non choisie, contact, arrêt brusque (il y en a une qui finit par se pousser)
Finteract: répulsion que quand elles sont vraiment proches, attraction à une longueur de 2 fourmis
--> La force d'interaction entre fourmis du même groupe est à revoir...
* Analyse spatiale du flux
That would bring some novelty on this data set
"Ces flux bidirectionnels qui se rencontrent, c'est assez rare: fourmis et piétons"
Quel est le modèle minimal qui donne le même résultat
Dirk Helbing Mehdi Moussaid
http://www.mehdimoussaid.com/laRecherche0311.pdf
https://www.complexity-explorables.org/explorables/the-walking-head/
Fouloscopie
Notes réu Tony
1 - Gestion des murs
Les murs seraient plutôt attractifs que répulsifs, avec une no-flux BC (projection de l'orientation). cf thigmotactisme
2 - Champ visuel
- le cône est bien adapté aux mouvements de détection avec antennes (osmotropotaxie)
- le champ visuel est très large mais très court et très flou
d_ref,same ~ 2 longueurs de fourmi
d_ref,other ~ 3 longueurs de fourmi
3 - Types de contacts
Choisis (attraction puis freinage smooth) ou non choisis (freinage brusque). À voir si on l’inclut dans le modèle.
4 - Analyse du modèle et utilité
Biologistes intéressés par l’analyse spatiale du flux / à voir si l’on peut trouver une sorte de loi sur les données, et comparer avec les simulations.
—> comprendre l’organisation spatiale.
Notes réu Thomas
Ancien
Nouveau
- Model : compactification + simplification (?)
- Lanes detection
Model simplification / compactification
\dot{X}_i = V_i \\
\dot{V}_i = \textcolor{blue}{F_{\text{self-prop}}} + \textcolor{red}{F_{\text{drive}}} + \textcolor{orange}{F_{\text{interact}}}
\textcolor{blue}{F_{\text{self-prop}}} = \nu \, (\xi - |V_i|) \Theta_i
1. Self-propulsion
\textcolor{orange}{F_{\text{interact}}} = \textcolor{orange}{F_{\text{same group}}} + \textcolor{orange}{F_{\text{other group}}}
\textcolor{red}{F_{\text{drive}}} = c_{\text{drive}} \, \begin{pmatrix} g_i \\ 0 \end{pmatrix}
\(\nu > 0\) strength of the force
\(\xi > 0\) target velocity magnitude
3. Interaction
2. Drive
drives to the right if \(g_i = 1\)
drives to the left if \(g_i = -1\)
\Theta_i = \frac{V_i}{|V_i|}
\textcolor{orange}{F_{\text{same group}}} = c_{\text{same}} \underset{g_j = g_i}{\sum_{j \in \mathcal{V}_i}}
\left(\frac{d_{\text{ref},1}}{|X_j - X_i|} \right)^{\alpha_{\text{same}}} \; \log \left(\frac{d_{\text{ref},1}}{|X_j - X_i|} \right) \; \frac{X_j - X_i}{|X_j - X_i|}
\textcolor{orange}{F_{\text{other group}}} = \underset{g_j \neq g_i}{\sum_{j \in \mathcal{V}_i}}
c_{\text{other}} \, \mathbf{1}_{d_{\text{contact}} < |X_j - X_i| < d_{\text{ref},2}} \, \frac{X_j - X_i}{|X_j - X_i|} \; \; +
\; \; \mathbf{1}_{|X_j - X_i| < d_{\text{contact}}} \, \textcolor{purple}{F_{ij}^{\text{steer}}}
Some level of redundancy
Model
\dot{X}_i = V_i,
V_i = u_i \; \hat{\Theta}_i,
\hat{\Theta}_i = \begin{pmatrix} \cos \theta_i \\ \sin \theta_i \end{pmatrix},
g_i \in \{-1,1\}
(X_i, V_i) \longrightarrow (X_i, u_i, \theta_i)
\dot{V}_i = \sum F
\dot{u}_i = \left(\sum F\right) \cdot \hat{\Theta}_i
\dot{\theta}_i = \left(\frac{1}{u_i}\sum F\right) \cdot \hat{\Theta}_i^{\perp}
We take inspiration from the previous model to built a simpler and more precise one
Model
\dot{X}_i = V_i,
V_i = u_i \; \hat{\Theta}_i,
\hat{\Theta}_i = \begin{pmatrix} \cos \theta_i \\ \sin \theta_i \end{pmatrix},
\mathrm{d} \theta_i =
\left(\textcolor{grey}{c}\sin(\textcolor{grey}{\omega} - \theta_i) - g_i \, \textcolor{blue}{k} \, \sin \theta_i \right) \mathrm{d}t
+ \sqrt{2 \textcolor{blue}{\zeta}} \; \mathrm{d} B_t^i
g_i \in \{-1,1\}
\textcolor{blue}{\xi}, \textcolor{blue}{\nu_{\rm c}} > 0
constant
cruising
\textcolor{blue}{k} > 0
constant
drive
\textcolor{grey}{\nu_{\rm b}}
not constant
braking
\textcolor{grey}{c,\omega}
not constant
attraction and steering
\textcolor{blue}{\zeta} \geqslant 0
constant
noise
\dot{u}_i = (\textcolor{blue}{\nu_{\rm c}} + \textcolor{grey}{\nu_{\rm b}})
\left( \frac{\textcolor{blue}{\nu_{\rm c}}}{\textcolor{blue}{\nu_{\rm c}} + \textcolor{grey}{\nu_{\rm b}}} \, \textcolor{blue}{\xi} - u_i \right),
Model
\dot{X}_i = V_i,
V_i = u_i \; \hat{\Theta}_i,
\hat{\Theta}_i = \begin{pmatrix} \cos \theta_i \\ \sin \theta_i \end{pmatrix},
\dot{u}_i = (\textcolor{blue}{\nu_{\rm c}} + \textcolor{grey}{\nu_{\rm b}})
\left( \frac{\textcolor{blue}{\nu_{\rm c}}}{\textcolor{blue}{\nu_{\rm c}} + \textcolor{grey}{\nu_{\rm b}}} \, \textcolor{blue}{\xi} - u_i \right),
\mathrm{d} \theta_i =
\left(\textcolor{grey}{c_{\rm int}}\sin(\textcolor{grey}{\omega} - \theta_i) - g_i \, \textcolor{blue}{k} \, \sin \theta_i \right) \mathrm{d}t
+ \sqrt{2 \textcolor{blue}{\zeta}} \; \mathrm{d} B_t^i
g_i \in \{-1,1\}
\textcolor{blue}{\xi}, \textcolor{blue}{\nu_{\rm c}} > 0
constant
cruising
\textcolor{blue}{k} > 0
constant
drive
\textcolor{grey}{\nu_{\rm b}}
not constant
braking
\textcolor{grey}{c_{\rm int},\omega}
not constant
attraction and steering
\textcolor{blue}{\zeta} \geqslant 0
constant
noise
\dot{V}_i = \textcolor{blue}{\nu_{\rm c}} \, (\textcolor{blue}{\xi} - |V_i|) \hat{\Theta}_i - \textcolor{grey}{\nu_{\rm b}} V_i
corresponds to
\dot{V}_i = F_{\rm interact} + F_{\rm drive}
comes from
(\(\hat{\Theta}_i\) part)
(\(\hat{\Theta}^\perp_i\) part)
Expression of \(\nu_b\)
\dot{u}_i = (\textcolor{blue}{\nu_{\rm c}} + \textcolor{grey}{\nu_{\rm b}})
\left( \frac{\textcolor{blue}{\nu_{\rm c}}}{\textcolor{blue}{\nu_{\rm c}} + \textcolor{grey}{\nu_{\rm b}}} \, \textcolor{blue}{\xi} - u_i \right),
\textcolor{grey}{\nu_{\rm b}} = \textcolor{blue}{\overline{\nu}_{\rm b} }
\underset{\hat{\Theta}_i \cdot \sigma_{ij} \geqslant \textcolor{blue}{c_{\rm b}}}{\sum_{j \in \mathcal{V}_i}}
\exp\left(- \left(\frac{|X_i - X_j|}{\textcolor{blue}{l_{\rm b}}} \right)^{\textcolor{blue}{\alpha_{\rm b}}} \right)
+
X_i
\hat{\Theta}_i
+
\sigma_{ij} = \frac{X_j - X_i}{|X_j - X_i|}
X_j
Cruising and braking
\textcolor{blue}{l_{\rm b},} \, \textcolor{blue}{\alpha_{\rm b}}
pilot the range of interaction
\textcolor{blue}{c_{\rm b}}
pilots the window of braking
\textcolor{blue}{c_{\rm b}} = 0.9
\(\alpha \sim 2 \implies\) term negligible when \(|X_j - X_i|\gtrsim 3 \, l_{\rm b} \)
\(\alpha \sim 3 \implies\) term negligible when \(|X_j - X_i|\gtrsim 2 \, l_{\rm b} \)
\textcolor{blue}{\overline{\nu}_{\rm b}} = 100 \nu_c
+
X_i
\hat{\Theta}_i
+
\sigma_{ij} = \frac{X_j - X_i}{|X_j - X_i|}
X_j
\mathrm{d} \theta_i =
\left(\textcolor{grey}{c_{\rm int}} \sin(\textcolor{grey}{\omega} - \theta_i) - g_i \, \textcolor{blue}{k} \, \sin \theta_i \right)
\mathrm{d}t
+ \sqrt{2 \textcolor{blue}{\zeta}} \; \mathrm{d} B_t^i
\textcolor{grey}{c_{\rm int}} \begin{pmatrix} \cos \textcolor{grey}{\omega_i} \\ \sin \textcolor{grey}{\omega_i} \end{pmatrix} =
\sum_{j_{\text{same}}\in \mathcal{V}_i} \textcolor{blue}{c_{\rm steer}}
\times (\hat{\Theta}_i \cdot \sigma_{ij})_+^2
\times \left(1 - \frac{|X_i - X_j|}{\textcolor{blue}{l_{\rm steer}}} \right)
\times \mathbf{1}_{|X_i - X_j| \leqslant \textcolor{blue}{l_{\rm steer}} } \; \sigma_{ij}^{\perp} \\
\qquad \qquad \qquad + \; \textcolor{blue}{c_{\rm attr}}
\times |\hat{\Theta}_i \cdot \sigma_{ij}^{\perp}|^2
\times \left(\frac{|X_i - X_j|}{\textcolor{blue}{l_{\rm steer}}} - 1 \right)
\times \mathbf{1}_{\textcolor{blue}{l_{\rm steer}} \leqslant |X_i - X_j| \leqslant \textcolor{blue}{l_{\rm attr}} }\sigma_{ij} \\
\sum_{j_{\text{other}}} \phantom{+ \;
\times \left(\frac{|X_i - X_j|}{\textcolor{blue}{l_{\rm steer}}} - 1 \right) \times \mathbf{1}_{\textcolor{blue}{l_{\rm steer}} \leqslant |X_i - X_j| \leqslant \textcolor{blue}{l_{\rm attr}} }\sigma_{ij}}
Attraction, steering and drive
+
X_i
\hat{\Theta}_i
+
\sigma_{ij} = \frac{X_j - X_i}{|X_j - X_i|}
X_j
- the more aligned, the stronger the steer
- the more perpendicular, the stronger the attraction
- linear decrease of the strength of the steer
- linear decrease of the strength of the attraction
g_i \in \{1,-1\}
Equation in orientation
drive
orientation decided differently for same and other
Full model
No reorientation "same"
Only steer in "same"
\sum_{j_{\text{same}}\in \mathcal{V}_i} \textcolor{blue}{c_{\rm steer}}
\times (\hat{\Theta}_i \cdot \sigma_{ij})_+^2
\times \left(1 - \frac{|X_i - X_j|}{\textcolor{blue}{l_{\rm steer}}} \right)
\times \mathbf{1}_{|X_i - X_j| \leqslant \textcolor{blue}{l_{\rm steer}} } \; \sigma_{ij}^{\perp} \\
\qquad \qquad \qquad + \; \textcolor{blue}{c_{\rm attr}}
\times |\hat{\Theta}_i \cdot \sigma_{ij}^{\perp}|^2
\times \left(\frac{|X_i - X_j|}{\textcolor{blue}{l_{\rm steer}}} - 1 \right)
\times \mathbf{1}_{\textcolor{blue}{l_{\rm steer}} \leqslant |X_i - X_j| \leqslant \textcolor{blue}{l_{\rm attr}} }\sigma_{ij} \\
\sum_{j_{\text{same}}\in \mathcal{V}_i} \textcolor{blue}{c_{\rm steer}}
\times (\hat{\Theta}_i \cdot \sigma_{ij})_+^2
\times \left(1 - \frac{|X_i - X_j|}{\textcolor{blue}{l_{\rm steer}}} \right)
\times \mathbf{1}_{|X_i - X_j| \leqslant \textcolor{blue}{l_{\rm steer}} } \; \sigma_{ij}^{\perp} \\
\qquad \qquad \qquad + \; \textcolor{blue}{c_{\rm attr}}
\times |\hat{\Theta}_i \cdot \sigma_{ij}^{\perp}|^2
\times \left(\frac{|X_i - X_j|}{\textcolor{blue}{l_{\rm steer}}} - 1 \right)
\times \mathbf{1}_{\textcolor{blue}{l_{\rm steer}} \leqslant |X_i - X_j| \leqslant \textcolor{blue}{l_{\rm attr}} }\sigma_{ij} \\
\sum_{j_{\text{same}}\in \mathcal{V}_i} \textcolor{blue}{c_{\rm steer}}
\times (\hat{\Theta}_i \cdot \sigma_{ij})_+^2
\times \left(1 - \frac{|X_i - X_j|}{\textcolor{blue}{l_{\rm steer}}} \right)
\times \mathbf{1}_{|X_i - X_j| \leqslant \textcolor{blue}{l_{\rm steer}} } \; \sigma_{ij}^{\perp} \\
\qquad \qquad \qquad + \; \textcolor{blue}{c_{\rm attr}}
\times |\hat{\Theta}_i \cdot \sigma_{ij}^{\perp}|^2
\times \left(\frac{|X_i - X_j|}{\textcolor{blue}{l_{\rm steer}}} - 1 \right)
\times \mathbf{1}_{\textcolor{blue}{l_{\rm steer}} \leqslant |X_i - X_j| \leqslant \textcolor{blue}{l_{\rm attr}} }\sigma_{ij} \\
Influençe of the terms in the "same" part
Steer without angle in "same"
\sum_{j_{\text{same}}\in \mathcal{V}_i} \textcolor{blue}{c_{\rm steer}}
\times (\hat{\Theta}_i \cdot \sigma_{ij})_+^2
\times \left(1 - \frac{|X_i - X_j|}{\textcolor{blue}{l_{\rm steer}}} \right)
\times \mathbf{1}_{|X_i - X_j| \leqslant \textcolor{blue}{l_{\rm steer}} } \; \sigma_{ij}^{\perp} \\
\qquad \qquad \qquad + \; \textcolor{blue}{c_{\rm attr}}
\times |\hat{\Theta}_i \cdot \sigma_{ij}^{\perp}|^2
\times \left(\frac{|X_i - X_j|}{\textcolor{blue}{l_{\rm steer}}} - 1 \right)
\times \mathbf{1}_{\textcolor{blue}{l_{\rm steer}} \leqslant |X_i - X_j| \leqslant \textcolor{blue}{l_{\rm attr}} }\sigma_{ij} \\
Steer without linear coefficient in "same"
\sum_{j_{\text{same}}\in \mathcal{V}_i} \textcolor{blue}{c_{\rm steer}}
\times (\hat{\Theta}_i \cdot \sigma_{ij})_+^2
\times \left(1 - \frac{|X_i - X_j|}{\textcolor{blue}{l_{\rm steer}}} \right)
\times \mathbf{1}_{|X_i - X_j| \leqslant \textcolor{blue}{l_{\rm steer}} } \; \sigma_{ij}^{\perp} \\
\qquad \qquad \qquad + \; \textcolor{blue}{c_{\rm attr}}
\times |\hat{\Theta}_i \cdot \sigma_{ij}^{\perp}|^2
\times \left(\frac{|X_i - X_j|}{\textcolor{blue}{l_{\rm steer}}} - 1 \right)
\times \mathbf{1}_{\textcolor{blue}{l_{\rm steer}} \leqslant |X_i - X_j| \leqslant \textcolor{blue}{l_{\rm attr}} }\sigma_{ij} \\
Influençe of the terms in the "other" part
Full model
\sum_{j_{\text{other}}\in \mathcal{V}_i} \textcolor{blue}{c_{\rm steer}}
\times (\hat{\Theta}_i \cdot \sigma_{ij})_+^2
\times \left(1 - \frac{|X_i - X_j|}{\textcolor{blue}{l_{\rm steer}}} \right)
\times \mathbf{1}_{|X_i - X_j| \leqslant \textcolor{blue}{l_{\rm steer}} } \; \sigma_{ij}^{\perp} \\
\qquad \qquad \qquad + \; \textcolor{blue}{c_{\rm attr}}
\times |\hat{\Theta}_i \cdot \sigma_{ij}^{\perp}|^2
\times \left(\frac{|X_i - X_j|}{\textcolor{blue}{l_{\rm steer}}} - 1 \right)
\times \mathbf{1}_{\textcolor{blue}{l_{\rm steer}} \leqslant |X_i - X_j| \leqslant \textcolor{blue}{l_{\rm attr}} }\sigma_{ij} \\
\sum_{j_{\text{other}}\in \mathcal{V}_i} \textcolor{blue}{c_{\rm steer}}
\times (\hat{\Theta}_i \cdot \sigma_{ij})_+^2
\times \left(1 - \frac{|X_i - X_j|}{\textcolor{blue}{l_{\rm steer}}} \right)
\times \mathbf{1}_{|X_i - X_j| \leqslant \textcolor{blue}{l_{\rm steer}} } \; \sigma_{ij}^{\perp} \\
\qquad \qquad \qquad + \; \textcolor{blue}{c_{\rm attr}}
\times |\hat{\Theta}_i \cdot \sigma_{ij}^{\perp}|^2
\times \left(\frac{|X_i - X_j|}{\textcolor{blue}{l_{\rm steer}}} - 1 \right)
\times \mathbf{1}_{\textcolor{blue}{l_{\rm steer}} \leqslant |X_i - X_j| \leqslant \textcolor{blue}{l_{\rm attr}} }\sigma_{ij} \\
No reorientation "other"
only steer in "other"
\sum_{j_{\text{other}}\in \mathcal{V}_i} \textcolor{blue}{c_{\rm steer}}
\times (\hat{\Theta}_i \cdot \sigma_{ij})_+^2
\times \left(1 - \frac{|X_i - X_j|}{\textcolor{blue}{l_{\rm steer}}} \right)
\times \mathbf{1}_{|X_i - X_j| \leqslant \textcolor{blue}{l_{\rm steer}} } \; \sigma_{ij}^{\perp} \\
\qquad \qquad \qquad + \; \textcolor{blue}{c_{\rm attr}}
\times |\hat{\Theta}_i \cdot \sigma_{ij}^{\perp}|^2
\times \left(\frac{|X_i - X_j|}{\textcolor{blue}{l_{\rm steer}}} - 1 \right)
\times \mathbf{1}_{\textcolor{blue}{l_{\rm steer}} \leqslant |X_i - X_j| \leqslant \textcolor{blue}{l_{\rm attr}} }\sigma_{ij} \\
\textcolor{grey}{c_{\rm int}} \begin{pmatrix} \cos \textcolor{grey}{\omega_i} \\ \sin \textcolor{grey}{\omega_i} \end{pmatrix} =
\sum_{j \in \mathcal{V}_i} c_{\rm steer}
\times (\hat{\Theta}_i \cdot \sigma_{ij})_+^2
\times \left(1 - \frac{|X_i - X_j|}{l_{\rm steer}} \right)
\times \mathbf{1}_{|X_i - X_j| \leqslant l_{\rm steer} } \; \sigma_{ij}^{\perp} \\
\qquad \qquad \qquad + \; c_{\rm attr}
\times |\hat{\Theta}_i \cdot \sigma_{ij}^{\perp}|^2
\times \left(\frac{|X_i - X_j|}{l_{\rm steer}} - 1 \right)
\times \mathbf{1}_{l_{\rm steer} \leqslant |X_i - X_j| \leqslant l_{\rm attr} }\sigma_{ij}
Observed use of each term
make more collisions
less lines head-to-back
less lines head-to-back
faster to get out from discussion
Goal: model
closeness and alignment criterion:
+
X_i
\hat{\Theta}_i
+
\sigma_{ij} = \frac{X_j - X_i}{|X_j - X_i|}
\begin{equation}
\frac{1 - \hat{\Theta}_i \cdot \sigma_{ij}}{\delta^2} + \left(\frac{|X_j-X_i|}{l}\right)^2 \leqslant 1 \qquad \phantom{x}
\end{equation}
Lane detection
Naive approach
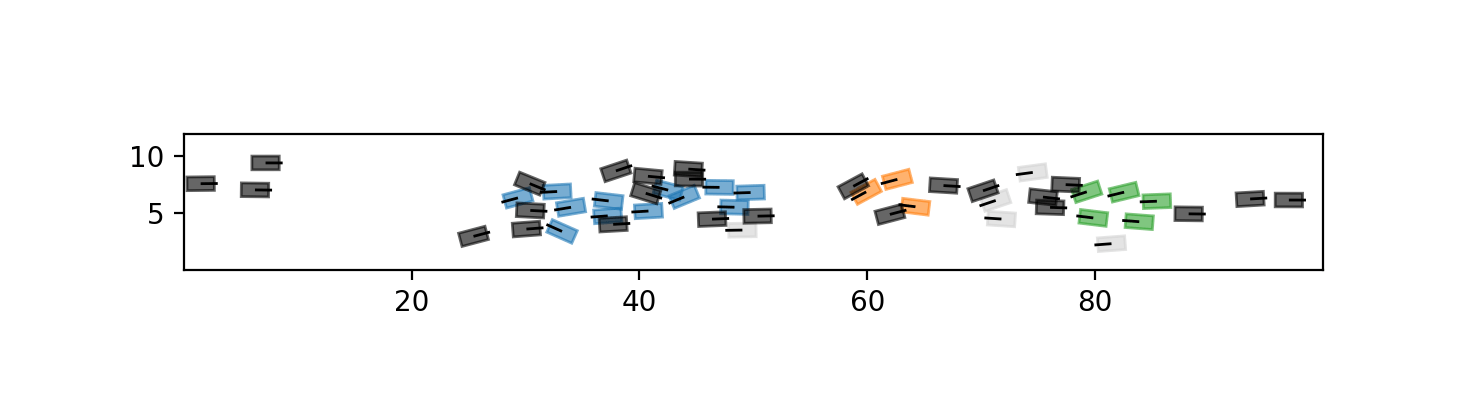
- We say that \(i\) follows \(j\) if
- A lane is a 'connex' component of agents that follow each other
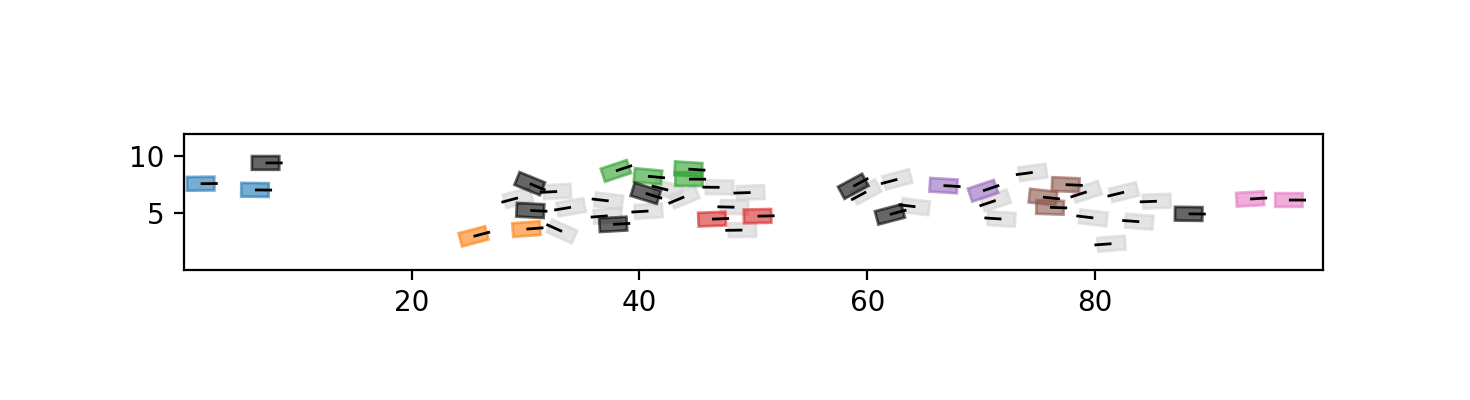
Lane detection
- Group by group (right and left)
- Sort agents by their \(x\)-position : \((i_1, i_2, \dots, i_N)\)
- Local criterion: \(i_{m}\) follows \(i_{n}\) if \(m \leqslant n\), \(\left|X_j - X_i \right| \leqslant l_1\) and \[\left( 1 - \cos \left(\theta_i - \varphi_{ij} \right) \right) \left|X_j - X_i \right|^\beta \leqslant \varepsilon \, l_1^\beta,\]
- \(\varepsilon > 0\), \(l_1 > l_0 > 0\) and \(\beta = \frac{-\log \varepsilon}{\log \frac{l_1}{l_0}}\)
- if \(i_m\) follows \(i_{n_1}, i_{n_2},\dots, i_{n_d}\), we group \(i_{m}\) with \(i_{n_1}, i_{n_2},\dots, i_{n_d}\) and all indices that any \(i_{n_k}\) follows
asks for \(i_m\) to head towards \(i_n\) and to be close to them. The closer, the less alignment is required, until \(|X_j-X_i|\leqslant l_0\) from which alignment no longer plays a a role
Reunion fourmis 2
By Thomas Borsoni
