Suorakulmainen kolmio
kateetit
hypotenuusa
Suorakulmaisessa kolmiossa on yksi suora kulma ja kaksi terävää kulmaa. Suoraa kulmaa vastapäätä olevaa sivua kutsutaan hypotenuusaksi, kahta muuta sivua kateeteiksi
\(c\)
\(a\)
\(b\)
Jos suorakulmaiselle kolmion jokaista sivua pitkin piirretään neliö, miten niiden pinta-alat liittyvät toisiinsa?
- \(3^2=9\)
- \(4^2=16\)
- \(5^2=25\)
- \(9+16=25\)
- \(3^2+4^2=5^2\)
Pythagoraan lause:
Jos kolmio on suorakulmainen ja sen kateettien pituudet ovat \(a\) ja \(b\) sekä hypotenuusan pituus \(c\), niin
\[a^2+b^2=c^2\]
Pythagoraan lauseen käänteislause:
Jos kolmion sivun pituuksille \(a\), \(b\) ja \(c\) pätee \(a^2+b^2=c^2\), niin kolmio on suorakulmainen.
Myös käänteinen pätee
Yksi todistus löytyy kirjasta, todistuksia on lukuisia muitakin
(huom. c:n pitää olla tässä pisin sivu)
Mikä on neliön sivun pituus, kun sen lävistäjä on 3?
\(x\)
\(x\)
Merkitään sivun pituutta kirjaimella \(x\)
\(x^2+x^2=3^2\)
\(2x^2=9\)
\(\parallel :2\)
\(x^2=\dfrac{9}{2}\)
\(\parallel \sqrt{\,}\)
\(x=\pm \sqrt{\dfrac{9}{2}}=\pm \dfrac{3}{\sqrt{2}}\)
Koska sivun pituus ei voi olla negatiivinen, \(x=\dfrac{3}{\sqrt{2}}\)
V: \(\dfrac{3}{\sqrt{2}}\)
3
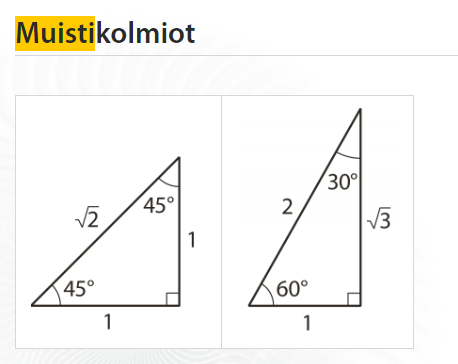
Tehtävän olisi voinut ratkaista myös yhdenmuotoisen muistikolmion avulla
\(x\)
\(x\)
3
\(\dfrac{x}{1}=\dfrac{3}{\sqrt{2}}\)
\(x=\dfrac{3}{\sqrt{2}}\)
Neliön puolikas:
Tasasivuisen kolmion puolikas:
Kolmion sivujen pituudet ovat \(14\), \(30\) ja \(33\). Onko kolmio suorakulmainen?
Käytetään Pythagoran käänteislausetta, eli katsotaan, toteuttavatko sivujen pituudet ehdon \(a^2+b^2=c^2\), jossa \(c\) on pisin sivu.
\(14^2+30^2=33^2\)
\(1096=1089\)
EPÄTOSI
V: Ei ole.
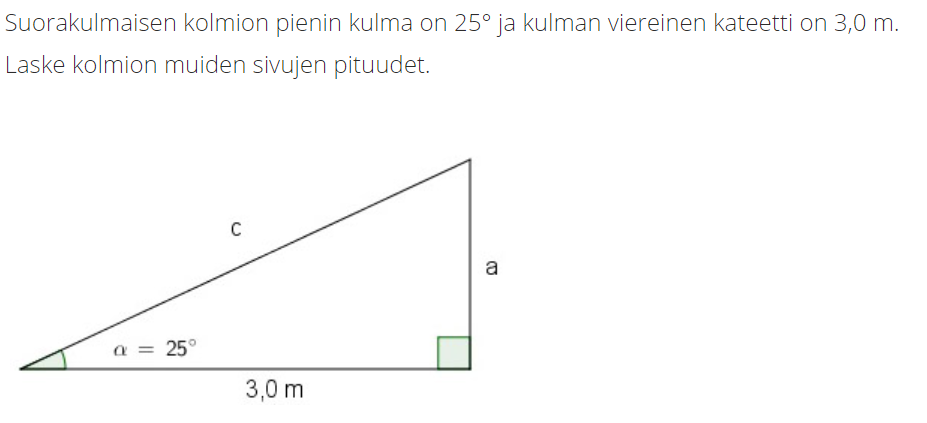
Suorakulmaisen kolmion sivujen suhteista saadaan muodostettua kulman sini, kosini ja tangentti
Kosini = komplementtikulman sini
∟
\(a\)
\(b\)
\(c\)
)
\(\alpha\)
\[\sin \alpha = \frac{b}{c}\]
\[\cos \alpha = \frac{a}{c}\]
\[\tan \alpha = \frac{b}{a}\]
Kun tiedetään kulman sinin arvo, voidaan kulman suuruus selvittää arkussinin avulla
Arkussiniä merkitään \(\arcsin x\) tai \(\sin^{-1}x\)
Esim.
\(\sin 40^\circ\approx 0{,}6428\), joten
\(\arcsin 0{,}6428\approx 40^\circ\)
Vastaavat arkusfunktiot löytyvät myös kosinille ja tangentille
Sekä nspiressä että speedcrunchissa äskeinen sini saadaan laskettua komennolla \(\texttt{sin(40)}\) ja arkussini komennolla \(\texttt{arcsin(0.6428)}\)
Vastaavasti cos, arccos, tan, arctan
Huom! Laskimesta pitää valita kulma-asetukseksi asteet
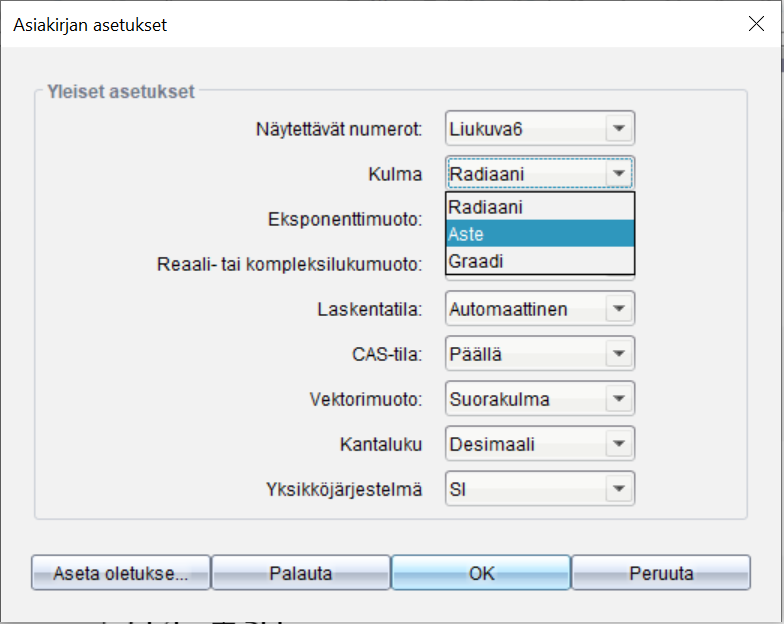
Nspire

Speedcrunch
05 Suorakulmainen kolmio
By Timo Pelkola
05 Suorakulmainen kolmio
- 53



