Hajontaluvut
| Lapsi | Ikä (kk) |
|---|---|
| 1 | 15 |
| 2 | 26 |
| 3 | 10 |
| 4 | 9 |
| 5 | 15 |
| 6 | 20 |
| 7 | 18 |
| 8 | 11 |
| 9 | 8 |
| 10 | 20 |
| 11 | 7 |
| 12 | 9 |
| 13 | 10 |
| 14 | 11 |
| 15 | 11 |
| 16 | 10 |
| 17 | 12 |
| 18 | 42 |
| 19 | 17 |
| 20 | 11 |
| 21 | 10 |
Taulukossa näkyy 21 eri lapsen iät kuukausina, jolloin lapsi puhui ensimmäistä kertaa
Kuinka paljon lasten iät poikkeavat toisistaan?
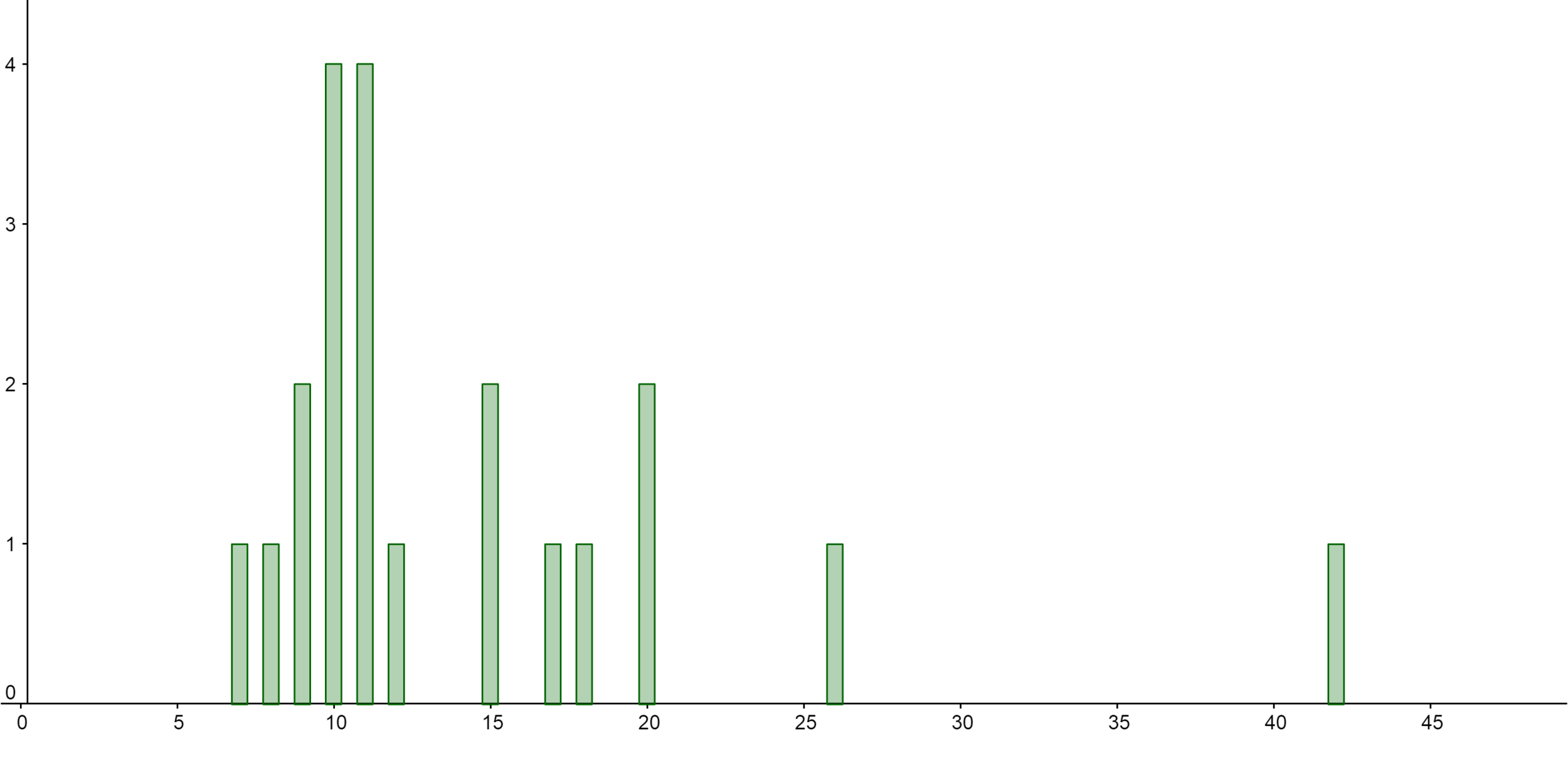
Paljonko lasten iät poikkeavat toisistaan?
Nuorin lapsista on 7 kk ja vanhin 42 kk,
eli vaihteluväli on [7, 42] kk.
Vanhimman ja nuorimman välinen ikäero,
eli vaihteluvälin pituus on siis 42 - 7 = 35 kk.
Ongelma: poikkeavat havainnot muuttavat
vaihteluväliä ja vaihteluvälin pituutta herkästi
Yksi ratkaisu: keskihajonta kertoo, mikä olisi "tavallista" vaihtelua. Taulukkolaskentaohjelmalla laskettuna se näyttäisi olevan 7,76 kk, mutta mitä se tarkoittaa?
(Populaation) keskihajonta (\(\sigma\)) on havaintoarvojen keskiarvosta laskettujen poikkeamien neliöiden keskiarvon neliöjuuri, eli
\(\sigma = \sqrt{\frac{(x_1-\bar{x})^2+(x_2-\bar{x})^2+...+(x_n-\bar{x})^2}{n}}\)
Otoksesta laskettaessa keskihajonta on kuitenkin otokseen suuntaan harhainen, jonka takia otoksesta yleensä lasketaan otoskeskihajonta (s)
\(s = \sqrt{\frac{(x_1-\bar{x})^2+(x_2-\bar{x})^2+...+(x_n-\bar{x})^2}{n-1}}\)
Huom! Taulukkolaskimessa keskihajonta on =KESKIHAJONTA() ja otoskeskihajonta =KESKIHAJONTA.S().
Tällä kurssilla käytetään aina otoskeskihajontaa
\(s = \sqrt{\frac{(x_1-\bar{x})^2+(x_2-\bar{x})^2+...+(x_n-\bar{x})^2}{n-1}}\)
Samalla tavalla kuin keskiarvo, keskihajontakin voidaan laskea frekvenssien avulla. Jos \(f_1,f_2,..,f_k\) on havaintomuuttujan mahdollisten arvojen \(x_1,x_2,..,x_k\) frekvenssit, niin
\(s = \sqrt{\frac{f_1(x_1-\bar{x})^2+f_2(x_2-\bar{x})^2+...+f_k(x_k-\bar{x})^2}{n-1}}\)
\(s= \sqrt{\frac{\sum\limits_{i=1}^k f_i(x_i-\bar{x})^2}{n-1}}\)
Summamerkin avulla kirjoitettuna:
Havainnon sanotaan poikkeavan merkittävästi, jos se on yli kahden keskihajonnan päässä keskiarvosta.

\(\bar{x}\)
\(\bar{x}+2s\)
\(\bar{x}-2s\)
Laske lukujen 3, 8, 7, 9 ja 33 otoskeskihajonta. Poikkeaako jokin luku merkittävästi?
\(s = \sqrt{\frac{(x_1-\bar{x})^2+(x_2-\bar{x})^2+...+(x_n-\bar{x})^2}{n-1}}\)
Lasketaan ensiksi keskiarvo:
\(\bar{x}=\dfrac{3+8+7+8+33}{5}=11{,}3\)
\(s=\sqrt{\dfrac{(3-11{,}3)^2+(8-11{,}3)^2+(7-11{,}3)^2+(9-11{,}3)^2+(33-11{,}3)^2}{5-1}}\)
\(\approx 10{,}82\)
Ei-poikkeavat havainnot ovat siis vähintään \(11{,}3-2\cdot10{,}82=-10{,}34\) ja enintään \(11{,}3+2\cdot10{,}82=32{,}94\), eli ne ovat välillä \([-10{,}34;32{,}94]\).
Luku 33 ei kuulu välille, joten se poikkeaa merkittävästi.
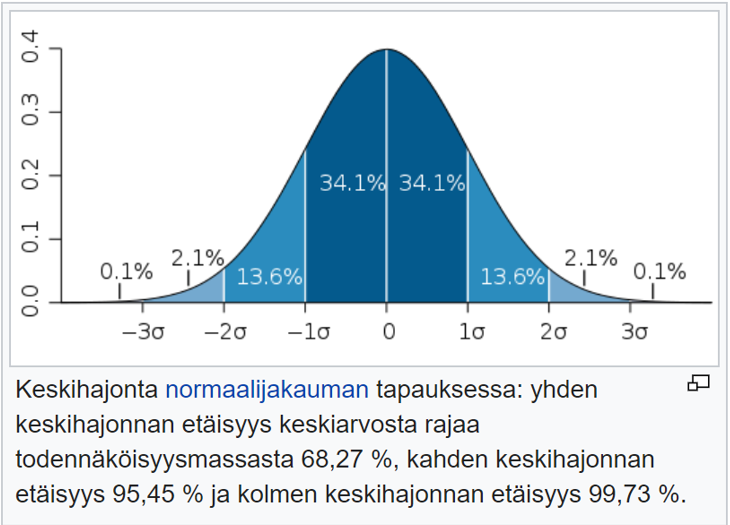
Kahden keskihajonnan päässä on normaalijakauman tapauksessa n. 95% havainnoista
04 Hajontaluvut
By Timo Pelkola
04 Hajontaluvut
- 86



