Regressio
Regressiossa kahden (tai useamman) tilastomuuttujan välinen riippuvuus pyritään esittämään halutunlaisen funktion muodossa niin, että funktion arvot poikkeavat mahdollisimman vähän todellisista arvoista
Selitysaste (\(r^2\)) on luku 0:n ja 1:n väliltä, joka kertoo, kuinka hyvin sovitettu funktio sopii havaintoaineistoon
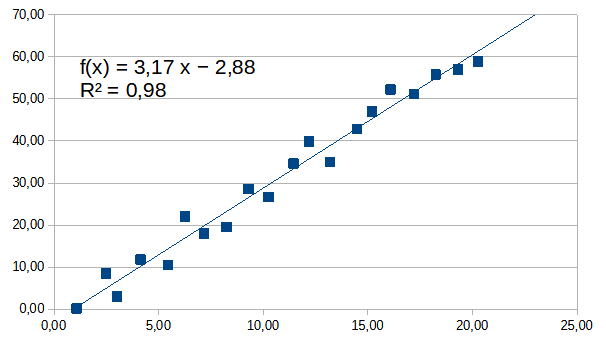
Selitysaste annetaan usein prosenttimuodossa.
Lisäksi käytetään puhetapaa:
x selittää y:n vaihtelusta 98%.
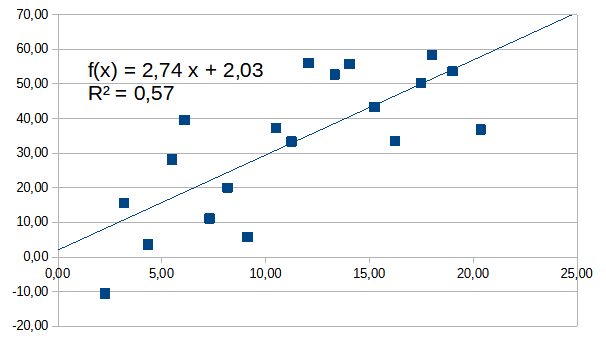
Alemmassa kuvassa
x selittää y:n vaihtelusta 57%.
Yleensä selittävä muuttuja on
x-akselilla, selitettävä muuttuja
y-akselilla.
Taulukossa on yrityksen somemainontaan kuukaudessa käyttämä raha ja kuukauden myynti euroina. Sovita aineistoon lineaarinen malli.
a) Paljonko mallin mukaan yksi mainontaan käytetty euro
kasvattaa myyntiä?
b) Ennusta mallin avulla, paljonko myynti olisi, jos
somemainontaan käytettäisiin 3000€ kuukausittain.
| Mainonta (€) | Myynti (€) |
|---|---|
| 1300 | 15362 |
| 1800 | 20212 |
| 2200 | 21951 |
| 2300 | 24162 |
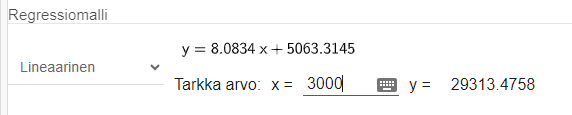
V: a) noin 8 euroa
b) noin 29 300 euroa
Jatkoa edelliselle.
c) Montako prosenttia mainonta selittää myynnin vaihtelusta?
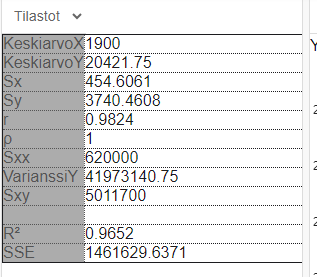
V: c) 97%

Huom! Korkeasta selitysasteesta huolimatta tämän mallin avulla ei voi luotettavasti arvioida sitä, paljonko mainonta kasvattaa myyntiä. Luultavasti myyntiä lisäävät myös muut asiat, jotka puuttuvat tästä mallista (ks. puuttuvan muuttujan harha).
06 Regressio
By Timo Pelkola
06 Regressio
- 65



