Trigonometriset funktiot
Yksikköympyrä
1
1
)
\(x\)
\((\cos x, \sin x)\)
Kulman kosini on kehäpisteen x-koordinaatti, sini y-koordinaatti
S2021
Jos \(0<x<\pi\), niin \(0<3x<3\pi\)
1
1
0,5
o
o
o
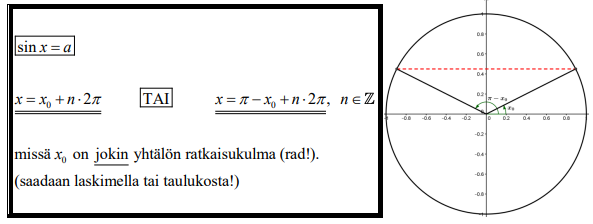
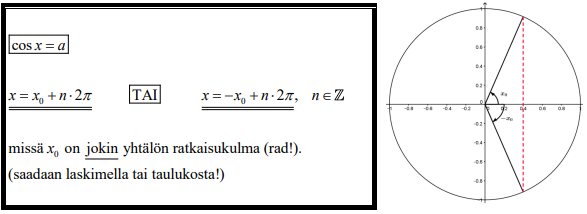
Jos tehtävä ei ratkea yksikköympyrää piirtämällä, MAOLissa ja koeympäristön ohjeissa on hyvin kattavasti paitsi trigonometrisia kaavoja, myös muuta tietoutta
Huom. MAOLissa "perusyhtälöt" ovat tyypillisimpiä tapauksia \(\sin x = a\) jne. ajatellen hieman hämmentävässä muodossa.
Myös tästä muodosta kuitenkin saa pääteltyä yhtälön \(\sin x = a\) ratkaisun, kun näkee, että \(y\) on "jokin ratkaisu"
S2020
Huom! Jos tehtävässä ei muuta mainita tai ole annettu mittoja yksikkönä metri tmv., vastaus halutaan tarkkana arvona. Tässä tehtävässä sattumalta tarkka arvo on asteina kokonaisluku, joten myös arkuskosinin ottaminen Speedcrunchilla tuottaa oikean vastauksen (muista valita kulma-asetukseksi asteet)
Radiaaneina tarkka arvo (\(x=\dfrac{3\pi}{4}\)) olisi kuitenkin jo helpompi selvittää taulukkokirjasta (trigonometristen funktioiden tarkkoja arvoja)
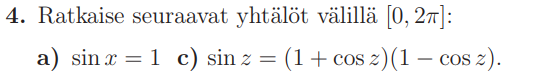
S2018
c-kohta:
1. avataan sulut
2. \(\sin^2 z + \cos^2 z = 1\), joten \(\cos^2 z = 1 - \sin^2 z\)
3. otetaan yhteinen tekijä \(\sin z\) ja ratkaistaan tulon nollasäännöllä
S2019
Tehtävän voisi ratkaista derivaatan avulla, mutta tehtävä ratkeaa myös ilman derivaattaa, kun muistaa sinin ja kosinin arvojoukon ([-1,1]) ja trigonometrian peruslauseen \(\sin^2 x + \cos^2 x = 1\)
S2020
1. kohdassa riitti solve
2. kohdassa solvesta saatu "false" ei riittänyt, vaan täytyi perustella esim. muokkaamalla yhtälöä:
\(\cos x \sin x + 1 = 0\) (koska \(\sin^2 x + \cos^2 x = 1\))
\(\dfrac{1}{2}\sin 2x + 1 = 0\) (koska \(\sin2x=2\sin x\cos x\))
\(\sin 2x = -2\) (ei ratkaisua, koska sinin arvojoukko [-1,1])
05 Trigonometriset funktiot
By Timo Pelkola
