Normittaminen
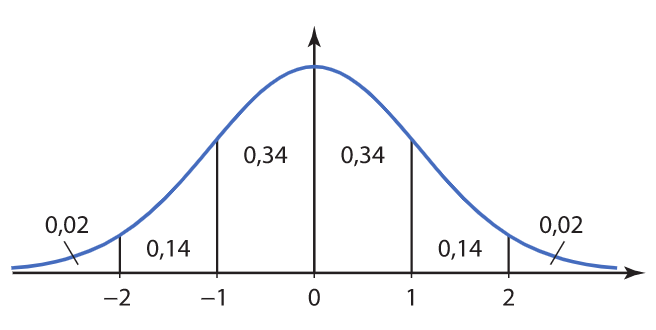
Normaalijakaumaa \(N(0,1)\), jonka odotusarvo on 0 ja keskihajonta 1, kutsutaan normitetuksi normaalijakaumaksi
Tiheysfunktio: \(\phi(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}x^2}\)
Jos \(X\sim N(\mu,\sigma)\), niin \(Z\sim N(0,1)\).
Satunnaismuuttuja \(X\) voidaan normittaa satunnaismuuttujaksi \(Z\) vähentämällä jokaisesta \(X\):n arvosta \(x\) odotusarvo \(\mu\) ja jakamalla keskihajonnalla \(\sigma\), eli \(Z\):n arvot \(z\) lasketaan
\(z=\frac{x-\mu}{\sigma}\)
\(P(X\leq x)=P(Z\leq z) = \Phi(z)\)
Todennäköisyyksiä voidaan laskea nyt normitetun satunnaismuuttujan avulla
\(N(0,1)\):n kertymäfunktion \(\Phi(x)\) arvoja löytyy taulukkokirjoista. Normitus antaa keinon laskea normaalijakautuneiden satunnaismuuttujien todennäköisyyksiä myös ilman laskimen erityistä normaalijakaumatoimintoa. Normituksesta voi olla myös hyötyä, jos odotusarvoa tai keskihajontaa ei tunneta.
Tehtaalla laadunvarmistaja Nasse hylkää nastat, joiden pituus on alle 9,950 mm tai yli 10,050 mm. Alimittaisia nastoja on 3% ja ylimittaisia nastoja 5%. Oletetaan, että nastojen pituus on normaalisti jakautunut. Mikä on nastojen pituuksien keskiarvo ja keskihajonta?
Merk. nastojen pituutta \(X\sim N(\mu, \sigma)\) ja \(Z\sim N(0,1)\)
Normitetut arvot: \(z_1=\frac{9,95-\mu}{\sigma}\) ja \(z_2=\frac{10,05-\mu}{\sigma}\)
\(P(X<9,950)=P(Z<z_1)=0,03\)

Eli \(z_1\approx -1,8808\)
\(P(X>10,050)=0,05\)
Eli \(z_2\approx 1,6449\)
\(P(X<10,050)=P(Z<z_2)=0,95\)

Normitetut arvot voi katsoa myös taulukkokirjasta!
Normitetut arvot: \(z_1=\frac{9,95-\mu}{\sigma}\) ja \(z_2=\frac{10,05-\mu}{\sigma}\)
Eli \(z_1\approx -1,8808\)
Eli \(z_2\approx 1,6449\)
Muodostetaan yhtälöryhmä
\(\begin{cases}z_1=-1,8808\\z_2=1,6449\end{cases}\)
\(\begin{cases}\frac{9,95-\mu}{\sigma}=-1,8808\\\frac{10,05-\mu}{\sigma}=1,6449\end{cases}\)
Laskimesta \(\mu \approx 10,003\) ja \(\sigma \approx 0,028\)
V: Nastan keskipituus 10,003 mm ja keskihajonta 0,028 mm
10 Normittaminen
By Timo Pelkola
10 Normittaminen
- 300



