Numeeriset menetelmät
A
B
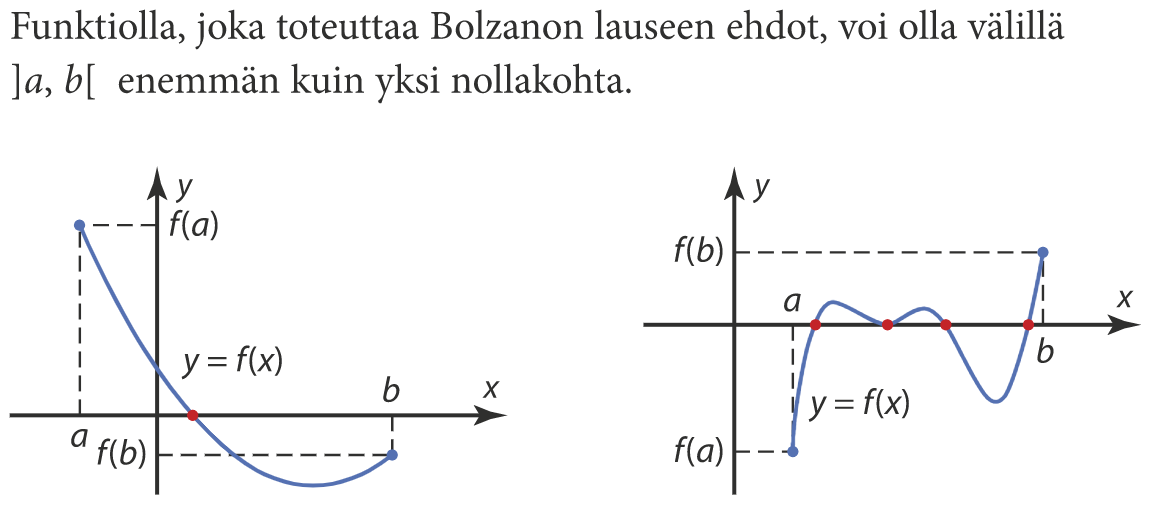
Voiko sinisen alueen pisteestä A piirtää yhtenäistä viivaa keltaisen alueen pisteeseen B ilman, että ylitetään punaista viivaa vähintään kerran?

Havaintoa kutsuttiin kurssilla MAA6 Bolzanon lauseeksi
Puolitusmenetelmä
- Puolitusmenetelmällä etsitään funktion nollakohdalle likiarvo käyttäen hyödyksi Bolzanon lausetta
- Puolitusmenetelmän ajatus on, että kun ollaan löydetty yksi Bolzanon lauseen toteuttava väli, ruvetaan väliä pienentämään
- Seuraavan välin päätepisteiksi valitaan aina edellisen välin keskipiste ja toinen edellisen välin päätepisteistä
- Koska välin päätepisteissä halutaan erimerkkiset arvot funktiolle, valitaan päätepisteeksi se, jolla tämä ehto toteutuu
- Näin välin pituus puolittuu jokaisella kierroksella
[
]
1. arvaus
x
- Uuden välin toiseksi päätepisteeksi tulee keskipiste ja toiseksi vanhan välin toinen päätepisteistä niin, että Bolzanon lause edelleen toteutuu eli funktion arvot on erimerkkiset
- Tässä tapauksessa uuden välin alkupisteeksi tulee keskipiste ja loppupisteeksi vanhan välin loppupiste

[
]
2. arvaus
x
- Uuden välin toiseksi päätepisteeksi tulee keskipiste ja toiseksi vanhan välin toinen päätepisteistä niin, että Bolzanon lause edelleen toteutuu eli funktion arvot on erimerkkiset
- Tässä tapauksessa uuden välin alkupisteeksi tulee keskipiste ja loppupisteeksi vanhan välin loppupiste

[
]
3. arvaus
x
- Uuden välin toiseksi päätepisteeksi tulee keskipiste ja toiseksi vanhan välin toinen päätepisteistä niin, että Bolzanon lause edelleen toteutuu eli funktion arvot on erimerkkiset
- Tässä tapauksessa uuden välin alkupisteeksi tulee vanhan välin alkupiste ja loppupisteeksi keskpiste

[
]
4. arvaus
x
- Uuden välin toiseksi päätepisteeksi tulee keskipiste ja toiseksi vanhan välin toinen päätepisteistä niin, että Bolzanon lause edelleen toteutuu eli funktion arvot on erimerkkiset
- Tässä tapauksessa uuden välin alkupisteeksi tulee vanhan välin alkupiste ja loppupisteeksi keskpiste

[
]
5. arvaus
x
- Uuden välin toiseksi päätepisteeksi tulee keskipiste ja toiseksi vanhan välin toinen päätepisteistä niin, että Bolzanon lause edelleen toteutuu eli funktion arvot on erimerkkiset
- Tässä tapauksessa uuden välin alkupisteeksi tulee vanhan välin alkupiste ja loppupisteeksi keskpiste
... tätä voidaan jatkaa. Keskipiste kuitenkin lähenee joka iteraatiolla nollakohtaa, eli se on nollakohdan likiarvo
Puolitusmentelmän yksi puolitusaskel voidaan siis kuvata seuraavasti:
Olkoon puolitettava väli \([a,b]\)
- Lasketaan välin keskipiste \(c=\dfrac{a+b}{2}\)
- Jos \(f(a)\) ja \(f(c)\) ovat erimerkkiset, niin uusi puolitettu väli on \([a,c]\)
- Muussa tapauksessa uusi puolitettu väli on \([c,b]\)
[
]
]
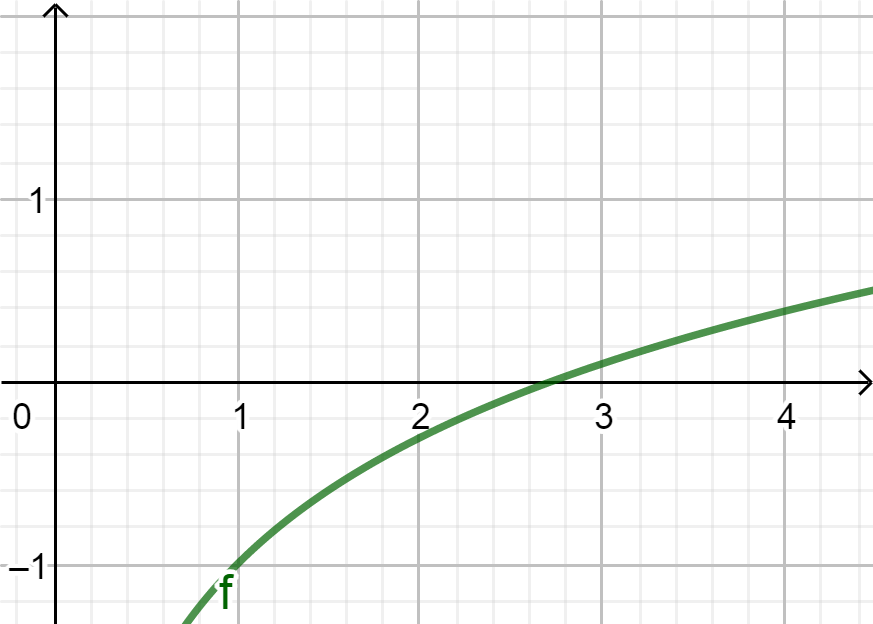
\(f(2)\) ja \(f(3)\) erimerkkiset
\(\Rightarrow\) uusi väli [2,3]
[
]
[
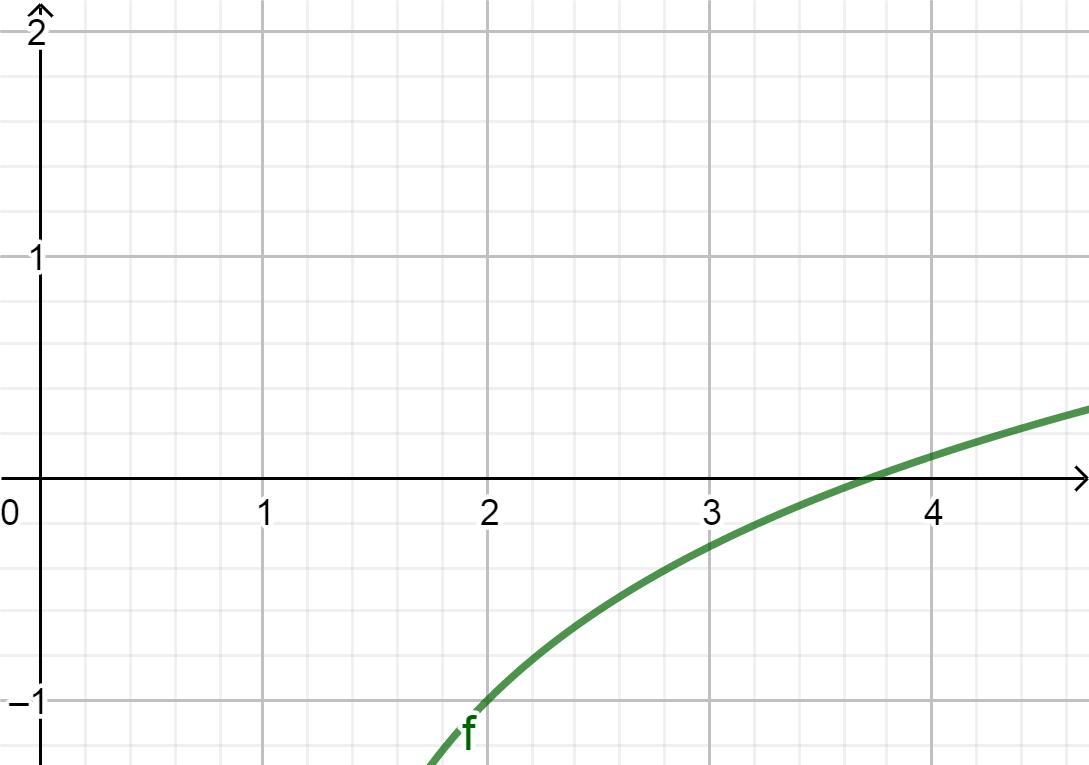
\(f(2)\) ja \(f(3)\) samanmerkkiset
\(\Rightarrow\) uusi väli [3,4]
Huom! Joskus harvoin sattuu niin, että \(f(c)=0\). Tällöin voidaan lopettaa puolittaminen tähän, koska nollakohta on sattumalta löytynyt.
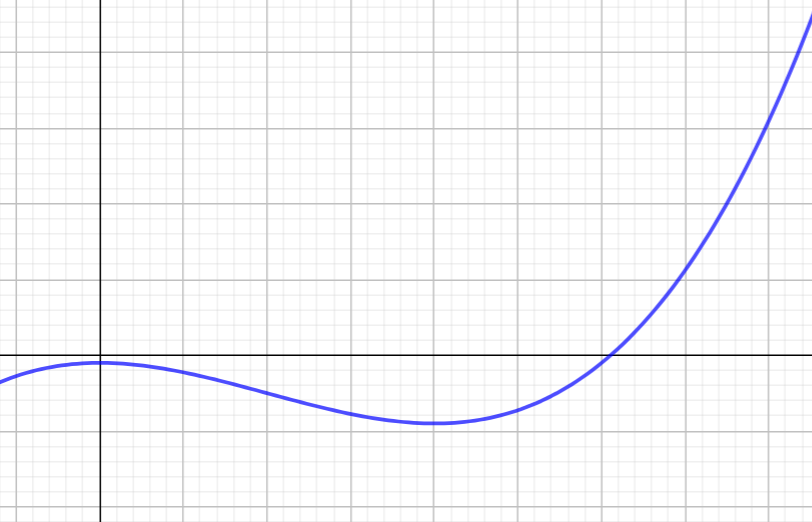
Esim. etsi funktion \(f(x)=\ln(x)-1\) nollakohdan likiarvo yhden desimaalin tarkkuudella käyttäen puolitusmentelmää. Aloita välistä \([2,3]\).
| a | b | c | f(a) ja f(c) erimerkkiset |
|---|---|---|---|
| 2 | 3 | 2.5 | epätosi |
| 2.5 | 3 | 2.75 | tosi |
| 2.5 | 2.75 | 2.625 | epätosi |
| 2.625 | 2.75 | 2.6875 | epätosi |
| 2.6875 | 2.75 | 2.71875 | tosi |
| 2.6875 | 2.71875 | STOP |
Koska välin \([a,b]\) molemmat päätepisteet pyöristyvät yhden desimaalin tarkkuudella samaan lukuun, niin \(x\approx 2{,}7\)
Erimerkkisyyden voi laskennallisesti todeta parilla eri tapaa:
- Jos \(f(a)\cdot f(c)<0\), \(f(a)\) ja \(f(c)\) ovat erimerkkiset
- Suorempi tapa olisi käyttää signum-funktiota (nspiressä sign(x), Pythonissa ei valmiina)
- \(\text{sign}(x)=\begin{cases}1, &x>0\\0, &x=0\\-1,&x<0\end{cases}\)
- Jos \(\text{sign}(f(a))\neq\text{sign}(f(c))\), \(f(a)\) ja \(f(c)\) ovat erimerkkiset
- Periaatteessa nopeampi tapa, käytännössä ei merkitystä
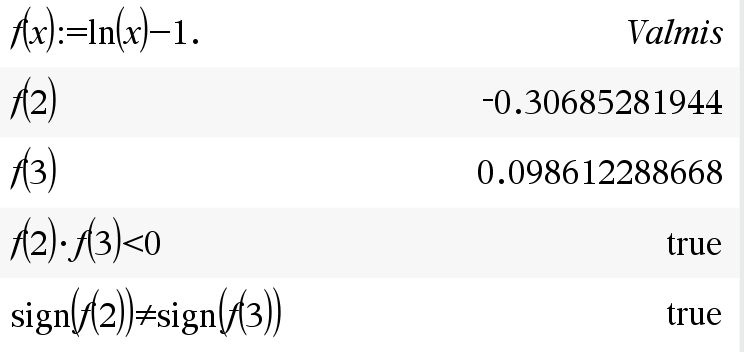
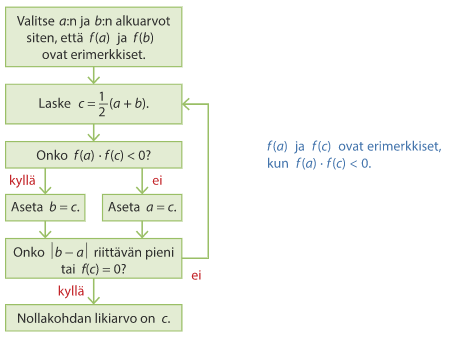
Puolitusmenetelmä voidaan esittää myös vuokaaviona
Etsi Pythonilla funktion \(f(x)=x^3-5x\) nollakohta välillä \([1,3]\)
a) käyttämällä 10 iteraatiota b) 4:n desimaalin tarkkuudella
a)
# Määritetään funktio Pythoniin
def f(x):
return x**3 - 5*x
# Asetetaan välin päätepisteille alkuarvot
a = 1.0
b = 3.0
for i in range(10):
c = (a + b)/2
if f(a)*f(c) < 0:
b = c
else:
a = c
print("Nollakohdan likiarvo on x = " + str(c))# Määritetään funktio Pythoniin
def f(x):
return x**3 - 5*x
# Asetetaan välin päätepisteille alkuarvot
a = 1.0
b = 3.0
while round(a,4) != round(b,4):
c = (a + b)/2
if f(a)*f(c) < 0:
b = c
else:
a = c
print("Nollakohdan likiarvo on x = " + str(round(c,4)))b) Komento round(x,n) pyöristää luvun x n:n desimaalin tarkkuudelle. Jatketaan toistoa niin kauan, kun a ja b eivät pyöristy samaan lukuun 4 desimaalin tarkkuudella
Puolitusmenetelmä nspiren taulukkolaskentaohjelmassa
- Määritä funktio laskimen puolella (f(x):=1.0*x^3-5x, kerro 1.0:lla jokin funktion termi, niin arvot lasketaan varmasti likiarvoina)
- Lisää Listat & taulukot -sovellus samaan asiakirjaan, ja taulukkolaskimeen sarakkeet "a", "b", "c" ja "erimerkkiset"
- Kirjoita alkuarvauksena ensimmäisen välin alku- ja loppupisteet (desimaalilukuna, 1.0 ja 3.0)
- Kirjoita keskipisteeseen ensimmäiselle riville kaava
=0.5*(A1+B1) (eli keskiarvo) - Kirjoita "erimerkkisiin" kaava =f(A1)*f(C1)<0 tai =sign(f(A1))\(\neq\)sign(f(C1))
- Kirjoita toiseksi alkupisteeksi kaava =iffn(D1,A1,C1)
- Kirjoita toiseksi loppupisteeksi kaava =iffn(D1,C1,B1)
- Vedä keskipisteeseen ja merkkiin kaavat edelliseltä riviltä
- Maalaa kaikki sarakkeet ja vedä alaspäin
- Luku on halutulla tarkkuudella, kun sekä ala- että yläraja pyöristyvät samaksi luvuksi (tai kun keskipiste vaikuttaa "stabiililta")
Esim. etsi taulukkolaskimella funktion \(f(x)=x^3-5x\) nollakohta välillä \([1,3]\) puolitusmenetelmällä 4:n desimaalin tarkkuudella
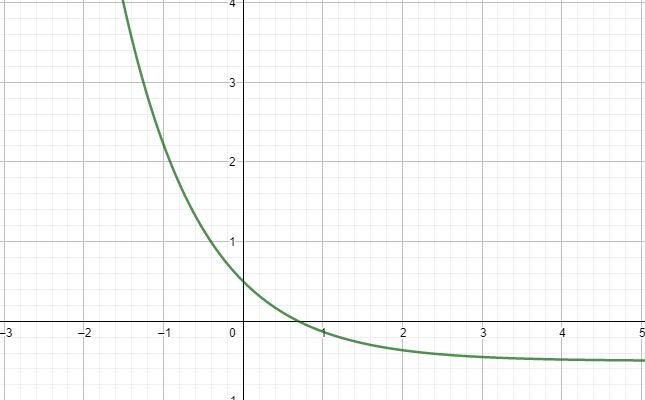
Puolitusmenetelmä perustui funktion jatkuvuuteen. Entä jos funktio olisi myös derivoituva, auttaako tämä nollakohdan likiarvon määritämisessä?
\(x_1\)
\(x_2\)
- Arvioidaan nollakohdaksi ensiksi alkuarvaus \(x_1\)
- Piirretään tähän kohtaan tangentti
- Uudeksi arvioksi nollakohdalle saadaan tangentin ja x-akselin leikkauskohta
- Toistetaan kohtia 2 ja 3
\(x_3\)
Derivoituvan funktion \(f\) kohtaan \(x_1\) piirretyn tangentin kulmakerroin on \(f'(x_1)\), ja tangentilta löytyy piste \((x_1,f(x_1))\).
Suoran yhtälön kaavasta tangentin yhtälöksi saadaan:
\(y-f(x_1)=f'(x_1)(x-x_1)\)
Nollakohdassa \(y=0\), joten
\(-f(x_1)=f'(x_1)(x-x_1)\)
Kun yhtälöstä ratkaistaan \(x\), saadaan
\(x=x_1-\frac{f(x_1)}{f'(x_1)}\),
jossa \(x\) on uusi arvio nollakohdalle
\[x_n=x_{n-1}-\frac{f(x_{n-1})}{f'(x_{n-1})}\]
Iteroimalla saadaan Newtonin menetelmän kaava
\[x_n=x_{n-1}-\frac{f(x_{n-1})}{\underbrace{f'(x_{n-1})}_{\neq 0}}\]
Huom! Derivoituvuuden lisäksi täytyy olettaa, ettei derivaatta ole iteraatiokohdissa nolla, koska muuten jaettaisiin nollalla.
Lukujonon \((x_n)\) jäsenet voidaan laskea kätevimmin iteroimalla funktiota
\[g(x)=x-\frac{f(x)}{f'(x)}\]
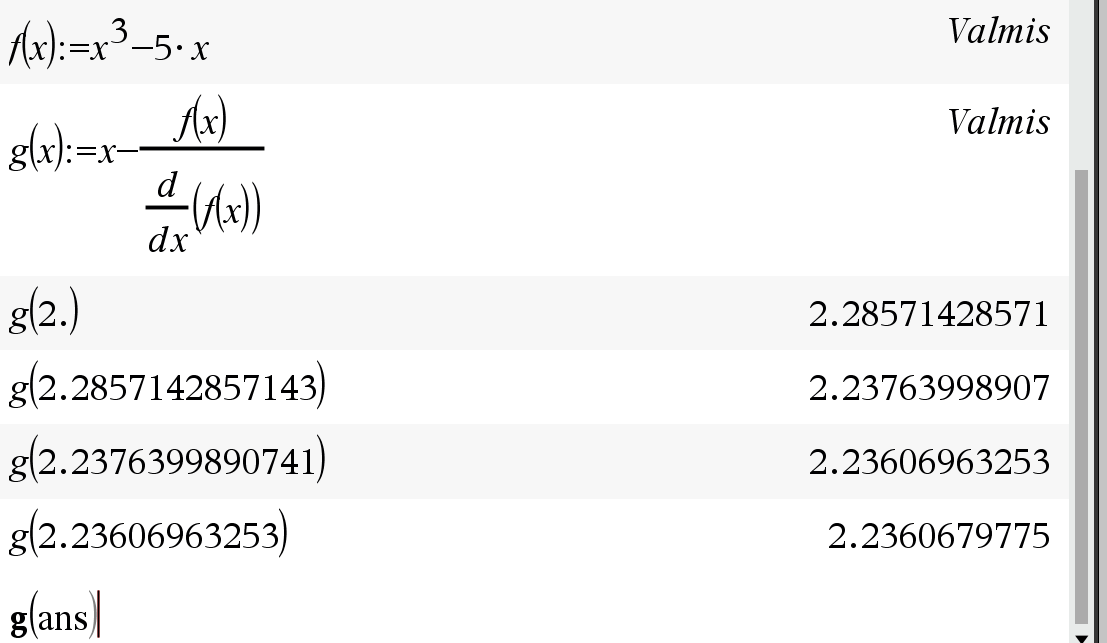
Funktion \(g(x)=x-\frac{f(x)}{f'(x)}\) iterointi nspiressä:
# Määritetään funktio Pythoniin
def f(x):
return x**3 - 5*x
# Määritetään funktion f derivaatta
def df(x):
return 3*x**2 - 5
# Määritetään iteroitava funktio g(x)
def g(x):
return x - f(x)/df(x)
# Asetetaan alkuarvaus
x = 2.0
for i in range(10):
x = g(x)
print("Nollakohdan likiarvo on x = " + str(x))Iterointi Pythonissa 10 kertaa:
Kuten puolitusmenetelmässäkin, alkuarvon valitsemiseksi on hyvä katsoa kuvaajaa, erityisesti jos funktiolla on useampi nollakohta
Nyrkkisääntönä alkuarvo pitäisi olla "riittävän lähellä" haluttua nollakohtaa, mutta kokeilemalla asia selviää helpoiten
Varoitus: aina Newtonin menetelmä ei suppene kohti mitään nollakohtaa
11 Numeeriset menetelmät
By Timo Pelkola
11 Numeeriset menetelmät
- 306



