Vektorit

K2020

K2021 2

S2017

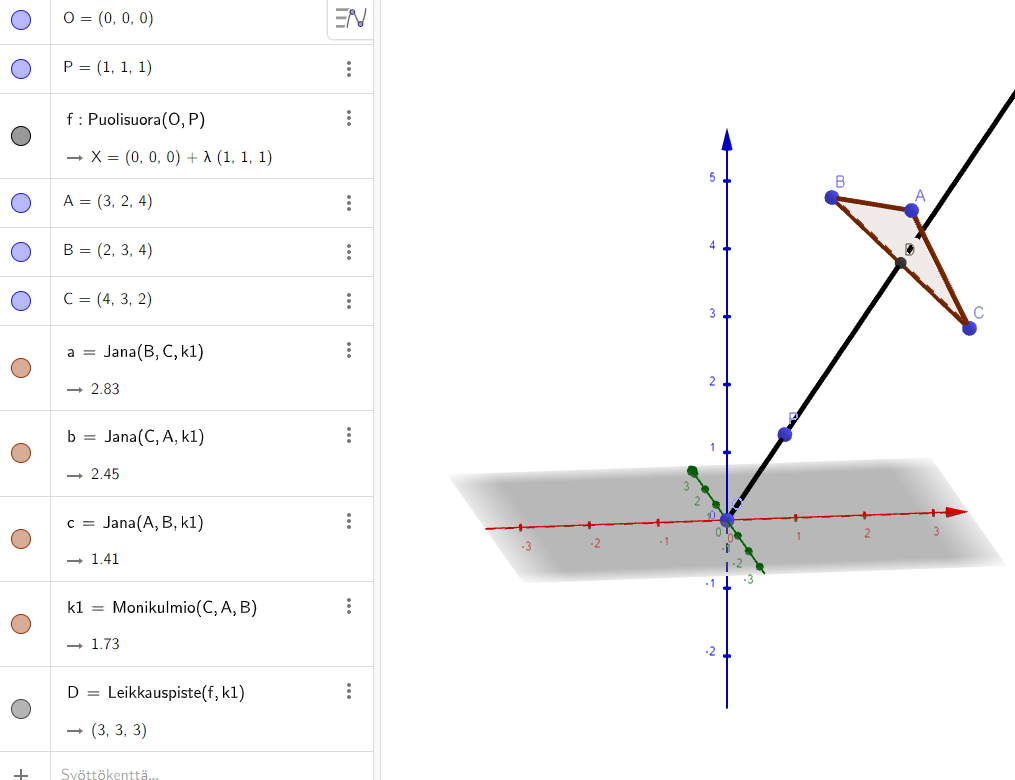
Puolisuoran pisteen \(P\) paikkavektori
\(\overline{OP}=t\bar{s}=t\bar{i}+t\bar{j}+t\bar{k}\) jollakin \(t\geq 0\).

Kolmion pisteen \(K\) paikkavektori on tehtävänannon mukaan
\(\overline{OK}=\alpha\bar{a}+\beta\bar{b}+\gamma\bar{c}=(3\alpha+2\beta+4\gamma)\bar{i}+(2\alpha+3\beta+3\gamma)\bar{j}+(4\alpha + 4\beta + 2\gamma)\bar{k}\), jossa \(\alpha + \beta + \gamma = 1\) ja \(\alpha,\beta,\gamma\geq 0\).

Puolisuora osuu kolmioon, jos \(\overline{OP}=\overline{OK}\).
Vektoreiden komponenttimuodon yksikäsitteisyyden vuoksi vektoreiden
\(\bar{i}\), \(\bar{j}\) ja \(\bar{k}\) kertoimet tulee olla yhtä suuret.

Saadaan:

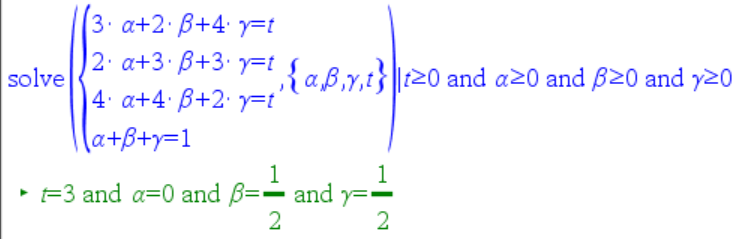
joten puolisuora osuu kolmioon (pisteessä (3,3,3))

Huom! Tehtävä olisi Geogebralla helppo, mutta syksyllä 2017 ei ollut vielä Geogebraa käytössä, vaikka CAS-laskin olikin.