🎄nalyyttinen
ge🔴metri🔔

K2021, kohdat 1-3 käyty viime kerralla
- selvitä aluksi kulmakerroin \(k\)
- tämän jälkeen voi joko
- käyttää suoran yhtälön kaavaa ja sieventää yhtälö ratkaistuun muotoon \(y=kx+b\) tai
- sijoittaa esim. pisteen (4,4) yhtälöön \(y=kx+b\) ja ratkaista b


🎅

S2021 6
- Voi joko ratkaista lähtien pisteen etäisyyden kaavasta tai huomaamalla, että kyse on ympyrästä, jonka keskipiste on (-3,1) ja säde 4. Jälkimmäiseen kysymykseen: funktio ei voi saada samassa kohdassa kahta eri arvoa.
- Voi ratkaista joko päättelemällä geometrisesti eri tapaukset (huom. pitää perustella myös, miksi nämä ovat ainoat tapaukset) tai huolehtimalla, että leikkauspisteitä on tasan yksi eli yhtälöparilla \(\begin{cases}x^2+(y-2)^2=4\\(x-1)^2+(y-2)^2=r^2\end{cases}\) on yksi ratkaisu
☃️
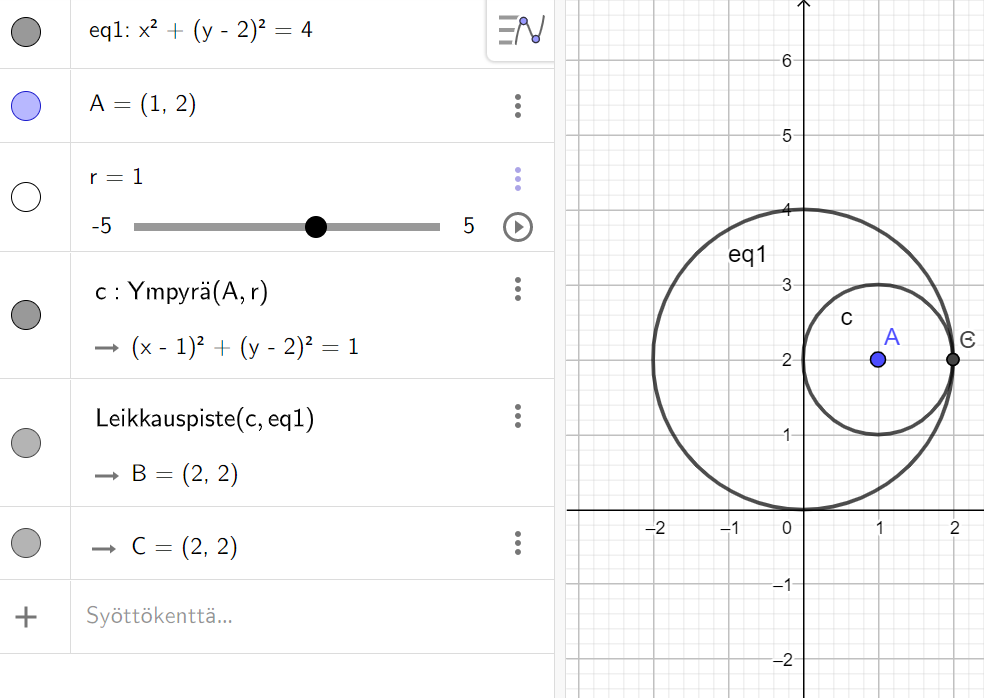
Kohdassa 2 on apua Geogebrasta.
Liukusäätimen saa, kun antaa ympyrän säteeksi r

(Voi myös asettaa ehdon, että yhtälöparista saatavan toisen asteen yhtälön diskriminantti \(D=0\))
Eräs mahdollinen analyyttinen ratkaisu

S2021, 1
Tapa 1:

🎁
Lisäksi pitäisi mainita: \(a\neq 0\)
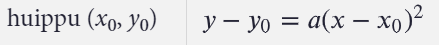

Tapa 2:
Lisäksi pitäisi mainita: \(y_0\neq 0\)
S2019

Tapoja on monia, esim.:
- piirretään geogebrassa ylös- ja alaspäin aukeavat paraabelit \(y=ax^2+bx+c\) ja \(y=ux^2+vx+w\) ja kokeillaan liukusäätimillä (+4p)
- kun on löydetty sopivat luvut ja kirjoitettu niitä vastaavat yhtälöt (+1+1p), muodostetaan ja ratkaistaan yhtälöpari (+2+1p)
- todetaan, että koska ratkaisuja eli leikkaupisteitä on vain yksi ja paraabelit aukeavat eri suuntiin, paraabeleiden täytyy sivuta toisiaan. (+2p) Tarkistetaan lopuksi, ettei sivuamispiste ole kummankaan paraabelin huippu (esim. Geogebralla). (1p)

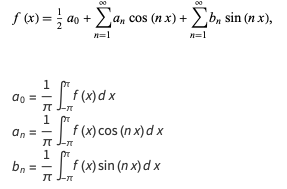

Fourier'n kaunis jouluinen pianosovitus

09 Analyyttinen geometria
By Timo Pelkola
09 Analyyttinen geometria
- 244



