Yksinkertainen korko
Kuinka paljon on \(81\%\) luvusta 72?
\(0{,}81\cdot 72 = 58{,}32\)
Muutetaan prosentti ensiksi desimaaliluvuksi ja kerrotaan desimaaliluvulla
Pikakertaus:
- Korko (r) on korvaus ajasta, jolloin raha ei ole omistajansa käytössä. Korvaus maksetaan korkokannan (i, esim. 1,4%) mukaan.
- Koron saajan näkökulmasta korko on tuloa, josta maksetaan pääomaveroa
- Jos korkotulo on peräisin talletuksista, pääomaveroa kutsutaan lähdeveroksi, jonka pankki maksaa asiakkaan puolesta. Lähdevero pyöristetään alaspäin lähimpään kymmeneen senttiin.
- Lähdeveron jälkeen jäävä korko on nettokorkoa, eli mitä pankkitallettaja oikeasti saa käyttöönsä
Alkuperäinen pääoma (k)
Korko (r)
\(\begin{cases}\\\\\\\\\\\end{cases}\)
\(\begin{cases}\\\\\\\\\\\\\\\\\\\\\\\\\\\end{cases}\)
Kasvanut pääoma
||||
\(\begin{cases}\\\end{cases}\)
Vero
\(\begin{cases}\\\\\\\end{cases}\)
Nettokorko
- Yksinkertaisessa korkolaskussa korkoaika on korkeintaan yhden korkokauden (esim. vuoden), jolloin korko lasketaan pääomalle vain yhden kerran
- Koron (\(r\)) suuruus riippuu:
- Alkuperäisestä pääomasta (\(k\))
- (Netto)korkokannasta (\(i\))
- Korko-ajasta korkokausina (\(t\))
- \(r=kit\)
-
Kasvanut pääoma (\(K\)) on alkuperäinen pääoma korkoineen
- \(K = k + r = k + kit\)
Ellei muuta mainita, korkokausi on yleensä 1 vuosi
\(t = 8\text{ kk} = \frac{8}{12}\text{ vuotta}\)
Sijoitustilille talletetaan 12 300€. Tilin korkokanta on 2,6%. Korosta peritään 30% lähdevero. Tili lopetetaan kahdeksan kuukauden kuluttua. Paljonko tililtä saadaan rahaa?
\(i=2{,}6\%=0{,}026\)
\(k=12\,300\)
\(r=kit=12\,300\cdot0{,}026\cdot\frac{8}{12}=213{,}20\)
Lähdeveroa maksetaan \(0{,}3\cdot213{,}20=63{,}96{€}\), joka alaspäin kymmenen sentin tarkkuudelle pyöristettynä on 63,90€
Tililtä saadaan rahaa siis \(12\,300 + 213{,}20 - 63{,}90=12449{,}30\) (€)
Jos lähdeveron pyöristyssääntöä ei huomioitaisi, äskeisen tehtävän olisi voinut laskea myös nettokorkokannan avulla.
Koska 30% korosta menee lähdeveroihin, jäljelle korosta jää
100%-30%=70%. Nettokorkokanta on siis
\(i=0{,}7\cdot2{,}6\%=1{,}82\%=0{,}0182\)
Nyt korko \(r=kit=12300\cdot0{,}0182\cdot\frac{8}{12}=149{,}24\) (€)
Siis tililtä saa \(12\,300+149{,}24=12449{,}24\) (€)
Päivämäärien laskemiseen on omat sääntönsä:
1) Aloituspäivältä ei makseta korkoa, mutta lopetuspäivältä maksetaan.
2) Koska kuukausien ja vuosien pituudet vaihtelevat, tämä huomioidaan joko saksalaisella, englantilaisella tai ranskalaisella korkotavalla. Jos ei mainita muuta, niin tällä kurssilla käytetään aina saksalaista tapaa.
saksalainen: kaikki kuukaudet oletetaan 30 päivän pituisiksi ja vuodessa on 360 päivää
ranskalainen: kuukaudet ovat oikean pituisia, mutta vuodessa on 360 päivää
englantilainen: kuukaudet ovat oikean pituisia ja vuodessa on 365 tai 366 päivää karkausvuosina
Tilille, jonka nettokorkokanta on 1,82%, talletetaan 1000€ 1.2.2024, ja rahat nostetaan tililtä 1.6.2024.
Paljonko kertyy korkoa?
Saksalainen tapa:
Aika on 4 kk, joten \(t=\dfrac{4\cdot 30}{360}=\dfrac{121}{360}\)
\(r=kit=1000\cdot0{,}0182\cdot\dfrac{121}{360}\approx6{,}07\) (€)
\(k=1000\), \(i=1{,}82\%=0{,}0182\)
Tilille, jonka nettokorkokanta on 1,82%, talletetaan 1000€ 1.2.2024, ja rahat nostetaan tililtä 1.6.2024.
Paljonko kertyy korkoa?
Ranskalainen tapa:
2024 on karkausvuosi, joten helmikuussa on 29 päivää, mutta talletuspäivää ei lasketa mukaan. Maaliskuussa on 31 päivää, huhtikuussa 30 ja toukokuussa 31. Lisäksi lasketaan nostopäivä mukaan.
\(t=\dfrac{28+31+30+31+1}{360}=\dfrac{121}{360}\)
\(r=kit=1000\cdot0{,}0182\cdot\dfrac{121}{360}\approx 6{,}11\) (€)
\(k=1000\), \(i=1{,}82\%=0{,}0182\)
Tilille, jonka nettokorkokanta on 1,82%, talletetaan 1000€ 1.2.2024, ja rahat nostetaan tililtä 1.4.2024.
Paljonko kertyy korkoa?
Englantilainen tapa:
2024 on karkausvuosi, joten helmikuussa on 29 päivää, mutta talletuspäivää ei lasketa mukaan. Maaliskuussa on 31 päivää, huhtikuussa 30 ja toukokuussa 31. Lisäksi lasketaan nostopäivä mukaan.
\(t=\dfrac{28+31+30+1}{366}=\dfrac{121}{366}\)
\(r=kit=1000\cdot0{,}0182\cdot\dfrac{90}{366}=6{,}02\) (€)
\(k=1000\), \(i=1{,}82\%=0{,}0182\)
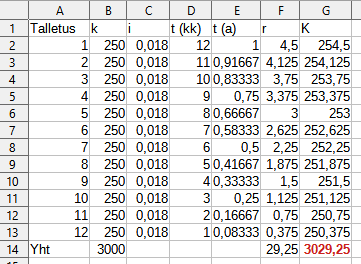
Korko lasketaan jokaiselle talletukselle erikseen. Ensimmäiselle talletukselle korkoaika on 12kk, viimeiselle 1kk.
Korot yhteensä:
\(250\cdot 0,018\cdot\frac{1}{12} + 250\cdot 0,018\cdot\frac{2}{12} + \cdots + 250\cdot 0,018\cdot\frac{12}{12}\)
Tilille, jonka nettokorko on 1,8%, säästetään kuukausittain 250€. Paljonko on vuoden päästä rahaa kasassa korkoineen?
Kaavoja:
E2: =D2/12
F2: =B2*C2*E2
G2: =F2+B2
B14: =summa(B2:B13)
F14: =summa(F2:F13)
G14: =summa(G2:G14)
\[=\frac{250\cdot 0,018}{12}\cdot (1+2+...+12)\]
\[=\frac{250\cdot 0,018}{12}\cdot 12\cdot \frac{1+12}{2}\]
Aritmeettinen summa
\(a_1 + \cdots + a_n = n \frac{a_1+a_n}{2}\)
\[=250\cdot 0,018\cdot 6,5=29,25\text{ (€)}\]
Talletusten kanssa: \(12\cdot 250 + 29,25 = 3029{,}25\text{ (€)}\)
01 Yksinkertainen korko
By Timo Pelkola
01 Yksinkertainen korko
- 285



