Kertymäfunktio
Tiheysfunktion määritelmä
Funktio \(f(x)\) on satunnaismuuttujan \(X\) tiheysfunktio, jos
- \(f(x)\geq 0\) kaikilla \(x\)
- \(\int \limits_{-\infty}^{\infty}f(x)\mathrm{d}x = 1\), eli x-akselin ja tiheysfunktion väliin jäävä pinta-ala on täsmälleen 1
- \(P(a\leq X\leq b)=\int \limits_{a}^{b}f(x)\,\mathrm{d}x\), eli välillä \([a,b]\) tiheysfunktion rajaama pinta-ala on todennäköisyys sille, että satunnaismuuttuja \(X\) saa arvon väliltä \([a,b]\)
- Huom! Sillä, otetaanko väliin päätepiste mukaan, ei ole merkitystä, eli \(P(a<X<b)=P(a\leq X\leq b)\)
- Tiheysfunktio \(f(x)\) integroimalla saadaan kertymäfunktio \(F(t)=\int \limits_{-\infty}^{t} f(x)\mathrm{d}x\)
- Vastaavasti kertymäfunktio derivoimalla saadaan tiheysfunktio
- Kertymäfunktion avulla voidaan laskea suoraan todennäköisyyksiä
- \(P(X\leq a)=F(a)\)
- \(P(X\geq a)=1-F(a)\)
- \(P(a\leq X\leq b)=F(b)-F(a)\)
Satunnaismuuttujan \(X\) tiheysfunktio on
\(f(x)=\begin{cases}\dfrac{1}{2\sqrt{x}},&0<x\leq 2\\0,&\text{muulloin}\end{cases}\).
Määritä satunnaismuuttujan \(X\) kertymäfunktio
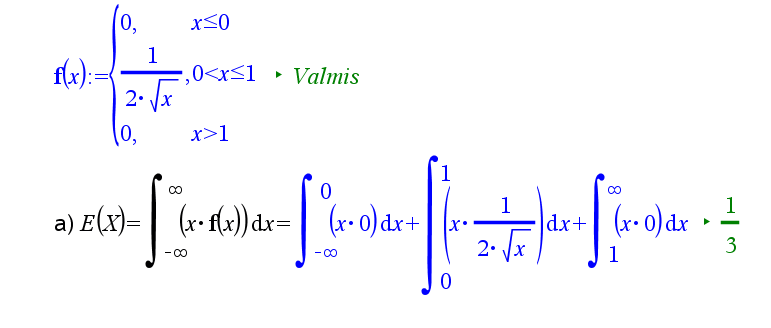
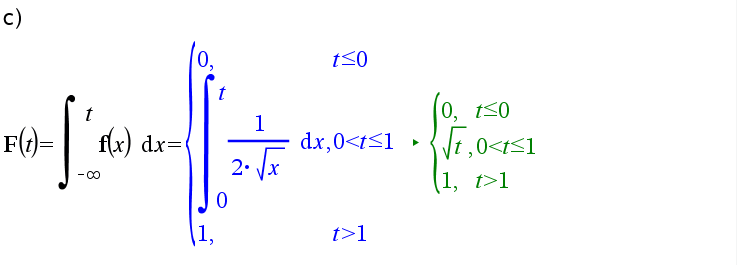
Huom. nspire ei tee eroa pienen f:n ja F:n väillä. Jos haluaa määritellä kertymäfunktion laskimeen, kannattaa valita toinen nimi, vaikka kf
08 Kertymäfunktio
By Timo Pelkola
