Diofantoksen yhtälö
Mitkä kokonaisluvut \(x\) ja \(y\) toteuttavat yhtälön \(2x+3y=12\)?
Esim. \(x=3\) ja \(y=2\) toteuttavat, koska \(2\cdot 3 + 3\cdot 2 = 12\)
Ratkaisuja on kuitenkin muitakin, ja ne löytyvät yhtälön \(2x+3y=12\) määrittämältä suoralta
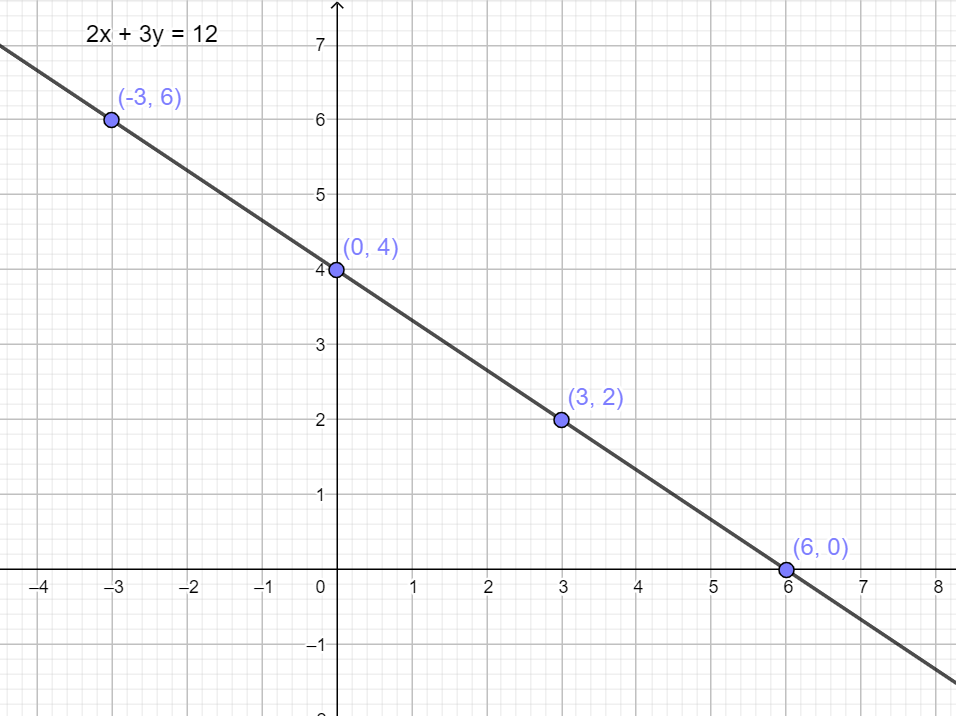
Miten ratkaisut löytäisi piirtämättä kuvaajaa?
Muotoa \(ax+by=c\) olevia yhtälöitä, joissa \(a,b,c,x,y\) ovat kokonaislukuja ja kertoimista \(a\) ja \(b\) ainakin toinen poikkeaa nollasta kutsutaan Diofantoksen yhtälöiksi
Lause Diofantoksen yhtälö \(ax+by=c\) on ratkeava, jos ja vain jos \(c\) on jaollinen lukujen \(a\) ja \(b\) suurimmalla yhteisellä tekijällä.
Kaikilla Diofantoksen yhtälöillä ei ole ratkaisuja, esim. ei ole sellaisia kokonaislukuja \(x\) ja \(y\), joilla \(9x+3y=4\)
Esim. yhtälö \(2x+3y=12\) on ratkeava, koska \(syt(2,3)=1\) ja \(1\mid12\)
Sen sijaan \(9x+3y=4\) ei ole ratkeava, koska \(syt(9,3)=3\), ja \(3\nmid 4\)
Jos Diofantoksen yhtälö on muotoa \(ax+by=syt(a,b)\), niin yksi ratkaisu löydetään Euklideen algoritmilla seuraavasti:
Etsi ratkaisu yhtälölle \(60x+36y=syt(60,36)\)
\(60 = 36\cdot 1 + \textcolor{pink}{24}\)
\(36 = 24\cdot 1 + \textcolor{pink}{12}\)
\(24 = 12\cdot 2\)
Siis \(syt(60,36)=12\) ja ratkaistava yhtälö on \(60x+36y=12\)
(eli \(12=60x+36y)\)
Ratkaistaan jakoyhtälöistä jakojäännökset
\(\textcolor{pink}{12} = 36 - 24\cdot 1\)
\(\textcolor{pink}{24} = 60 - 36\cdot 1\)
\(12=36-(60-36\cdot 1)\cdot 1\)
Lähdetään alimmasta yhtälöstä, ja sijoitetaan ylempi yhtälö siihen
\(=36 -60+36\)
\(=60\cdot (-1)+36\cdot 2\)
Eräs ratkaisu on siis \(x=-1\) ja \(y=2\)
Selvitetään \(syt(60,36)\)
Äskeisen perusteella voidaan nyt ratkaista myös yhtälö \(60x+36y=-24\), joka tiedetään ratkeavaksi, koska \(-24\) on suurimmalla yhteisellä tekijällä \(12\) jaollinen
\(12=60\cdot (-1)+36\cdot 2\)
\(\parallel \cdot (-2)\)
\(-24=60\cdot 2+36\cdot (-4)\)
Siis eräs yhtälön \(60x+36y=-24\) ratkaisu on \(x=2\) ja \(y=-4\)
Diofantoksen yhtälön \(ax+by=c\) ratkaiseminen kannattaa aloittaa siis aina lukujen \(a\) ja \(b\) suurimman yhteisten tekijän määrittelemisestä Euklideen algoritmilla
Lause Jos \(x=x_0\) ja \(y=y_0\) on eräs Diofantoksen yhtälön \(ax+by=syt(a,b)\) ratkaisu, niin eräs ratkeavan yhtälön \(ax+by=c\) ratkaisu on \(x=\dfrac{c}{syt(a,b)}x_0\) ja \(y=\dfrac{c}{syt(a,b)}y_0\)
Edellinen huomio voidaan yleistää:
Lause Jos \(x=x_0\) ja \(y=y_0\) on yksi Diofantoksen yhtälön \(ax+by=c\) ratkaisu, kaikki ratkaisut ovat muotoa
\(x=x_0+\dfrac{b}{syt(a,b)}n\) ja \(y=y_0-\dfrac{a}{syt(a,b)}n\), jossa \(n\in\mathbb{Z}\).
Esim. edellä huomattiin, että yhtälön
\(60x+36y=-24\) eräs ratkaisu on \(x=2\) ja \(y=-4\)
\(x=2+\dfrac{36}{syt(60,36)}n=2+\dfrac{36}{12}n= 2+3n\) ja
\(y=-4-\dfrac{60}{syt(60,36)}n=-4-\dfrac{60}{12}n=-4-5n\)
Kaikki ratkaisut ovat siis muotoa
Jokin toinen ratkaisu saadaan, kun sijoitetaan esim. \(n=2\):
\(x=2+3\cdot2=8\) ja \(y=-4-5\cdot2=-14\)
Entä muut ratkaisut?
Etsi Diofantoksen yhtälön \(172x+20y=1000\) kaikki ratkaisut
Selvitetään \(syt(172,20)\) Euklidkeen algoritmilla
\(172 = 20\cdot 8 + 12\)
\(20 = 12\cdot 1 + 8\)
\(12 = 8\cdot 1 + 4\)
\(8 = 4\cdot 2\)
Siis \(syt(172,20)=4\) ja yhtälö on ratkeava, koska \(4\mid1000\)
Ratkaistaan jakojäännökset
\(12 =172-20\cdot 8\)
\(8 = 20 -12\cdot 1\)
\(4 = 12- 8\cdot 1\)
Etsi Diofantoksen yhtälön \(172x+20y=1000\) kaikki ratkaisut
Ratkaistaan jakojäännökset
\(12 =172-20\cdot 8\)
\(8 = 20 -12\cdot 1\)
\(4 = 12- 8\cdot 1\)
\(4 = 12- 8\cdot 1\)
\(= 12- (20 -12\cdot 1)\cdot 1\)
Sijoitetaan jakojäännöksiä
Siis eräs yhtälön \(172x+20y=syt(172,20)\) ratkaisu on \(x=2\) ja \(y=-17\)
\(= 2\cdot 12-20\)
\(= 2\cdot (172-20\cdot 8)-20\)
\(= 172\cdot 2-20\cdot 16 - 20\)
\(= 172\cdot2+20\cdot (-17)\)
Etsi Diofantoksen yhtälön \(172x+20y=1000\) kaikki ratkaisut
Siis eräs yhtälön \(172x+20y=syt(172,20)\) ratkaisu on \(x=2\) ja \(y=-17\)
Eräs yhtälön \(172x+20y=1000\) ratkaisu on siten \(x=\dfrac{1000}{syt(172,20)}\cdot 2=\dfrac{1000}{4}\cdot 2 = 500\) ja
\(y=\dfrac{1000}{syt(a,b)}\cdot(-17)=\dfrac{1000}{4}\cdot(-17)=-4250\)
Yhtälön kaikki ratkaisut ovat muotoa:
\(x=500+\dfrac{20}{syt(172,20)}n=500+\dfrac{20}{4}n=500+5n\) ja
\(y=-4250-\dfrac{172}{syt(172,20)}n=-4250-\dfrac{172}{4}n=-4250-43n\)
* Diofantoksen yhtälö
By Timo Pelkola
* Diofantoksen yhtälö
- 263



