Avaruusgeometria

S2021

Harvinaisempi 100% Geogebralla ratkaistava tehtävä

• Silmämääräisesti piirtäminen ei riitä! Käytä oikeita työkaluja. Approksimaatioratkaisulla on saanut max 4 pistettä. Ratkaisussa tulee tuoda ilmi, miten siihen ollaan päädytty.
• Kun piirrät pohjan, kannattaa kiertää näkymää niin, että katsot xy-tasoa suoraan ylhäältä päin. Valitse yhden pohjan sivun päätepisteiksi esim. origo ja (1,0,0), jolloin sivun pituus on 1.
• Myös tasasivuisten kolmioiden sivujen pituus täytyy olla 1. Kaikki yhden etäisyydellä olevat pisteet löytyy 1-säteisen pallon pinnalta, joiden keskipisteinä on 5-kulmion kärjet.
• Huippupiste löytyy pohjan keskipisteeseen piirretyn keskinormaalin ja pallon leikkauspisteestä. Keskipisteen saa kulmanpuolittajien leikkauspisteestä.
• Kun mittaat kulmia, mieti ensiksi, minkä kolmion kulma kyseinen avaruuskulma on. Jos jokin kolmion pisteistä ei ole valmiiksi näkyvillä, mieti, miten saisit sen näkyville.

K2021

• Tässä tarkan kolmiuloitteisen kuvan piirtäminen on Geogebralla hankalaa "etukäteen" eli ratkaisematta ensiksi mikä R on.
• Avaruusgeometriassa tärkeä taito on osata palauttaa ongelma tasogeometriaan. Piirrä tilanne eri suunnista katsottuna, tässä ylhäältä ja sivusta. KolourPaint riittää hyvin myös mallikuvien piirtämiseen.

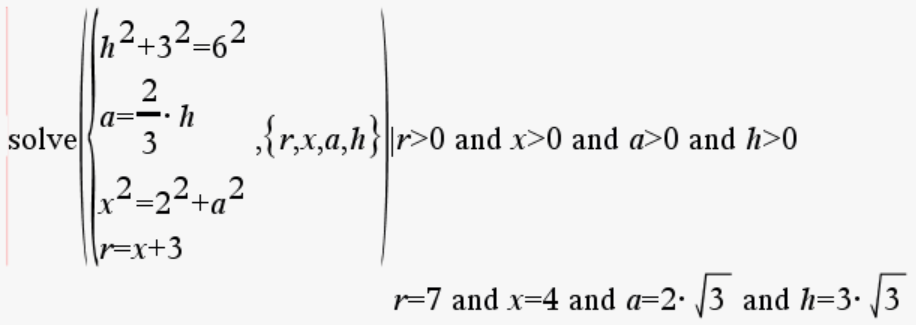
Kun on saanut yhtälöt muodostettua, välituloksia ei tarvitse välttämättä laskea, vaan yhtälöt voi syöttää myös suoraan yhtälöryhmään.