Derivointi ja derivaatan arvo
Viime tunnilla:
\(f'(c)\) on funktion \(f\) kuvaajalle kohtaan \(x=c\)
piirretyn tangentin kulmakerroin.
\(x\)
\(y\)
\(c\)
\(y=f(x)\)
\(\Delta x\)
\(\Delta y\)
Jos funktion \(f(x)\) lauseke tunnetaan, ja se on riittävän yksinkertainen (esim. polynomifunktio), voidaan derivaattafunktion \(f'(x)\) lauseke päätellä.
Tätä kutstuaan derivoinniksi.
Jos funktion derivaatta selvitetään jokaisella muuttujan arvolla \(x\), saadaan derivaattafunktio \(f'(x)\).
Piirrä Geogebrassa funktion \(f(x)=x^2\) kuvaaja. Lisää kuvaajalle piste johonkin kohtaan, ja piirrä tähän kohtaan tangentti. Siirtele pistettä ja täytä taulukko käyttäen apuna tangentin kulmakerrointa. Päättele derivaattafunktion \(f'(x)\) lauseke.
| x | f'(x) |
|---|---|
| -2 | |
| -1 | |
| 0 | |
| 1 | |
| 2 | |
| 3 |
\(-4\)
\(-2\)
\(0\)
\(2\)
\(4\)
\(6\)
\(=2\cdot(-2)\)
\(=2\cdot(-1)\)
\(=2\cdot(0)\)
\(=2\cdot1\)
\(=2\cdot2\)
\(=2\cdot3\)
\(=2x\)
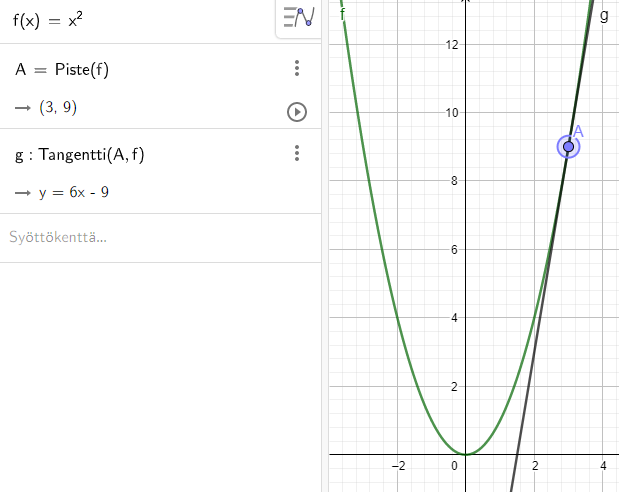
Yritetään keksiä derivointisääntö muille potenssifunktiolle, esim.
\(f(x)=x^5\)
Käytetään säännön keksimisessä apuna nspiren derivointiominaisuutta
\(f'(x)=5x^4\)
Mitä potenssifunktiossa lausekkeelle näyttää tapahtuvan?
\(5\)
\(x\)

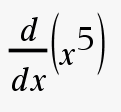
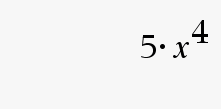
\(5\)
\(x\)
\(4\)
Vanha asteluku tulee eteen kertoimeksi, ja asteluku pienenee yhdellä!
Yritetään keksiä derivointisääntö muille potenssifunktiolle, esim.
\(f(x)=x^5\)
Käytetään säännön keksimisessä apuna nspiren derivointiominaisuutta
\(f'(x)=5x^4\)
Mitä potenssifunktiossa lausekkeelle näyttää tapahtuvan?

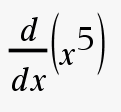
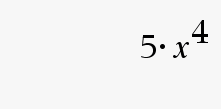
Yleisesti:
Potenssifunktion \(f(x)=x^n\) derivaattafunktio on \(f'(x)=nx^{n-1}\)
Ts. potenssifunktiota derivoidessa vanha asteluku tulee eteen kertoimeksi, ja asteluku pienenee yhdellä
Derivoidessa käytetään myös seuraavanlaista merkintää:
\(\mathrm{D}(x^n)=nx^{n-1}\)
Esim.
\(\mathrm{D}(x^3)\)
\(=3x^{3-1}=3x^2\)
\(\mathrm{D}(x^8)\)
\(=8x^{8-1}=8x^7\)
Derivointisääntöjä:
Summan derivaatta on derivaattojen summa:
Vakiokerroin säilyy:
\(\mathrm{D}(k\cdot f(x))=k\cdot f'(x)\)
\(\mathrm{D}(f(x)+g(x)) = f'(x)+g'(x)\)
Esim. \(D(x^2+x^6)=2x+6x^5\)
Esim. \(D(5x^3)=5\cdot 3x^2=15x^2\)
Vakion derivaatta on 0
\(\mathrm{D}(c) = 0\)
Esim. \(\mathrm{D}(5)=0\)
\(\mathrm{D}(a\cdot x)=a\)
Esim. \(\mathrm{D}(3x)=3\)
Potenssifunktion derivointikaavasta voidaan päätellä myös, että
Derivoi
\(f(x)=3x^2-5x+1\)
\(f'(x)=3\cdot2x^{1}-5+0\)
\(=6x-5\)
Laske funktion \(f\) derivaatan arvo kohdassa 3
\(f'(3)=6\cdot 3 -5=18-5=13\)
07 Derivointi ja derivaatan arvo
By Timo Pelkola
07 Derivointi ja derivaatan arvo
- 19



