Jatkuva tilastomuuttuja
| Haukka | Pyrstö (mm) |
|---|---|
| 1 | 219 |
| 2 | 221 |
| 3 | 235 |
| 4 | 230 |
| 5 | 212 |
| 6 | 243 |
| 7 | 210 |
| 8 | 238 |
| 9 | 222 |
| 10 | 217 |
| ... | ... |
Aineistossa on 577:n Amerikanhiirihaukan pyrstön pituudet millimetreinä. Miten pyrstön pituudet ovat jakautuneet?
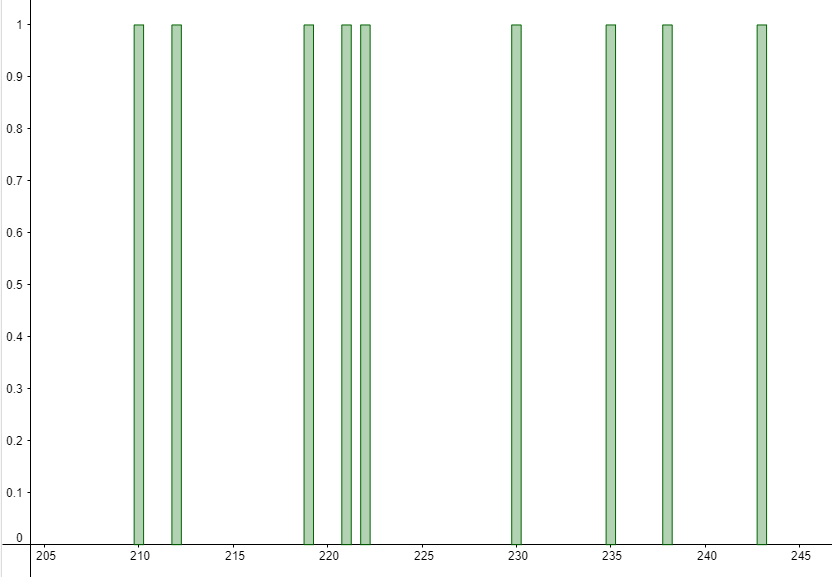
10:n ensimmäisen havainnon frekvenssejä tarkastelemalla ei selviä mitään, koska kaikki ovat 1
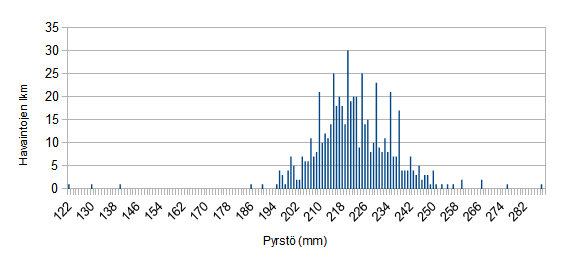
Piirtämällä kaikista 577 havainnosta pylväsdiagrammi saadaan jakaumaa jo hieman näkyville.
?!?!?
Mutta nyt diagrammissa näkyy omituisia piikkejä, jotka tuskin vastaavat todellisuutta.
Voiko kahdella haukalla ylipäätään olla täsmälleen samanpituinen pyrstö, vai onko mittaustarkkuus vain liian pieni?
Toisaalta mittaustarkkuuden lisääminen johtaisi äskeisen kaltaiseen tilanteeseen: kaikkien pituuksien frekvenssi olisi 1, emmekä osaisi sanoa jakaumasta mitään.
Kokeillaankin vähentää tarkkuutta! Luokitellaan havainnot 10 millimetrin välein.
Nyt jakaumaa on helpompi tulkita. Esim. kaikista eniten on sellaisia haukkoja, joiden pyrstönpituus on 230-239 mm.
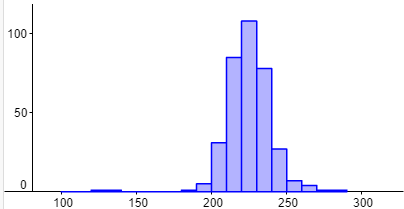
Kyseessä ei kuitenkaan ole enää pylväsdiagrammi vaan histogrammi.
Jatkuva tilastomuuttuja
- Jatkuva tilastomuuttuja voi diskreetistä tilastomuuttujasta poiketen saada mitä tahansa arvoja joltakin väliltä
- Esim. pituus, aika jne.
- Mahdollisia arvoja on siis periaatteessa ääretön määrä
- Frekvenssin laskemisesta suoraan ei hyötyä: useimpien havaittujen arvojen frekvenssi on luultavasti 1, jos vain tarkkuus riittää
- Samasta syystä pylväsdiagrammi ei suoraan sovi kuvaamaan jatkuvaa muuttujaa
Luokittelu
- Jatkuva tilastomuuttuja voidaan luokitella esim. tasavälein halutun kokoisiin luokkiin
- Luokille lasketaan frekvenssi sen mukaan, moniko havaintoarvo osuu määritetylle välille
- Luokkaa vastaavaksi arvoksi voidaan valita välin keskipiste eli luokkakeskus
- Keskipiste pitäisi laskea todellisten rajojen mukaan. Jos esim. aineistossa on pituudet pyöristetty 1 mm:n tarkkuudelle tavanomaisella pyöristyssäännöllä, tällöin luokan "110-119 mm":n todelliset rajat ovat 109,5 mm ja 119,5mm, ja luokkakeskus \(\frac{109,5+119,5}{2}=114,5\).
- Luokan "15-19 -vuotiaat" alaraja taas on yleensä 15 ja yläraja 20, joten luokkakeskus on 17,5.
- Luokittelemalla jatkuvaa tilastomuuttujaa voidaan käsitellä kuin se olisi diskreetti tilastomuuttuja
- Keskiarvolle ja keskihajonnalle voidaan laskea likiarvo käyttäen luokkakeskusta ja luokan frekvenssiä samaan tapaan kuin diskreetille muuttujalle
11 Jatkuva tilastomuuttuja
By Timo Pelkola
11 Jatkuva tilastomuuttuja
- 16



