Käänteisfunktio
Olk. \(f:A\to A\), jossa lähtöjoukko ja maalijoukko \(A=\{1,2,3,4\}\)
Käännetään nuolien suunta, ja kutsutaan syntyvää funktiota \(g\):ksi
1
2
3
4
1
2
3
4
\(A\)
\(A\)
\(f\)
1
2
3
4
1
2
3
4
\(A\)
\(A\)
\(g\)
- \(f(1)=4\)
- \(f(2)=1\)
- \(f(3)=3\)
- \(f(4)=2\)
- \(g(1)=2\)
- \(g(2)=4\)
- \(g(3)=3\)
- \(g(4)=1\)
- \(f(1)=4\)
- \(f(2)=1\)
- \(f(3)=3\)
- \(f(4)=2\)
\(f(x)=y \Leftrightarrow g(y)=x\)
1
2
3
4
1
2
3
4
\(A\)
\(A\)
\(f\)
1
2
3
4
1
2
3
4
\(A\)
\(A\)
\(g\)
- \(g(1)=2\)
- \(g(2)=4\)
- \(g(3)=3\)
- \(g(4)=1\)
\(g\) on funktion \(f\) käänteisfunktio, merkitään \(g=f^{-1}\)
Määritä kuvaajasta \(f^{-1}(1)\), \(f^{-1}(2)\), \(f^{-1}(4)\) ja \(f^{-1}(8)\)
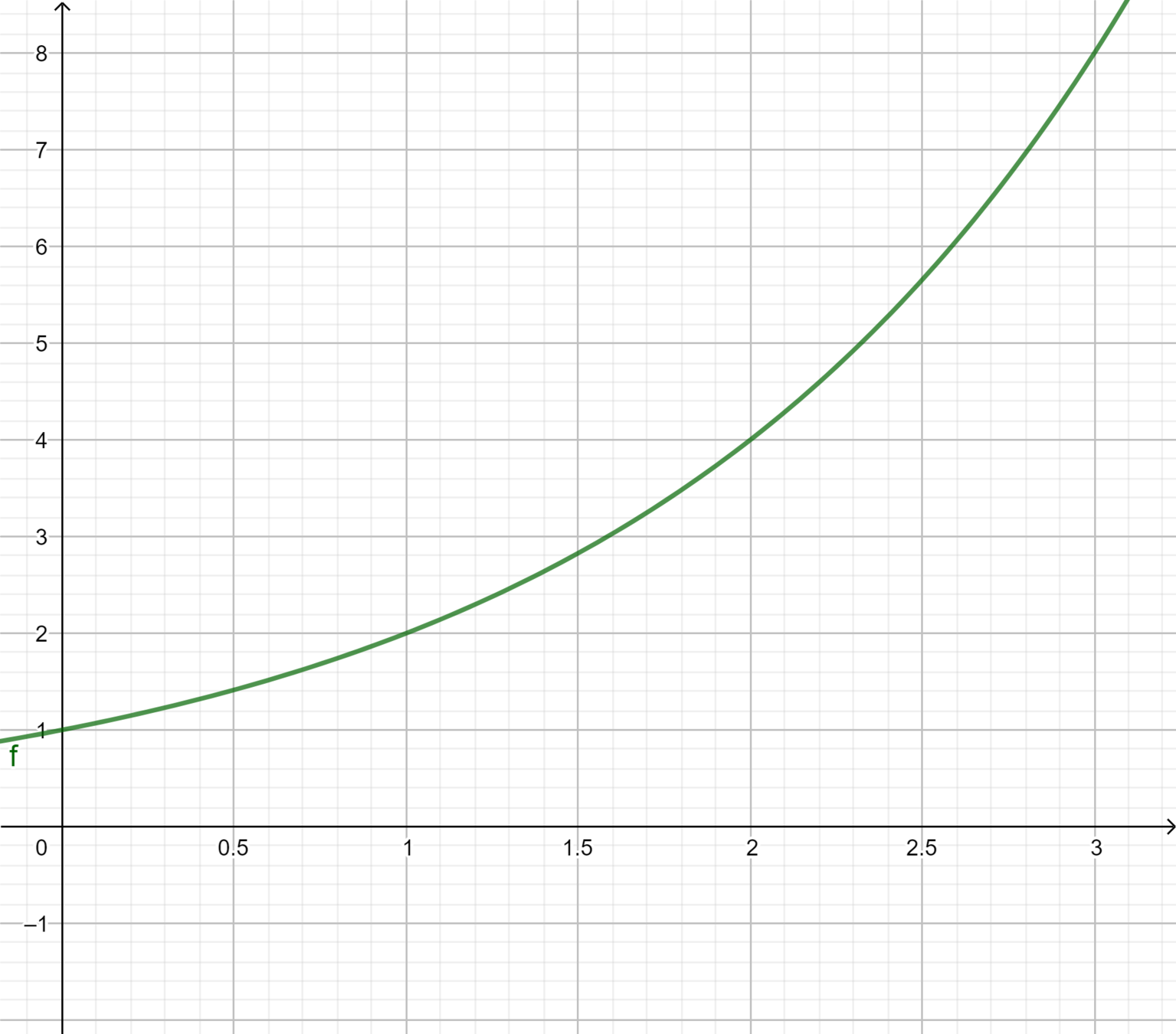
- \(f^{-1}(1)=0\)
- \(f^{-1}(2)=1\)
- \(f^{-1}(4)=2\)
- \(f^{-1}(8)=3\)
\(f(x)=y\Leftrightarrow f^{-1}(y)=x\)
\(f(x)=y\Leftrightarrow f^{-1}(y)=x\)
Olkoon \(f(x)=x^3+1\). Määritä käänteisfunktion lauseke \(f^{-1}(x)\).
Piirrä koordinaatistoon kuvaajat \(y=f(x)\), \(y=f^{-1}(x)\) ja \(y=x\). Mitä huomaat?
\(f(x)=y\)
Käänteisfunktion määritelmän mukaan \(f^{-1}(y)=x\). Ratkaistaan yo. yhtälöstä \(x\).
\(x^3+1=y\)
\(x^3=y-1\)
\(x=\sqrt[3]{y-1}\)
\(\parallel \sqrt[3]{\,}()\)
Siis. \(f^{-1}(y)=\sqrt[3]{y-1}\), joten \(f^{-1}(x)=\sqrt[3]{x-1}\).

Voi käyttää myös solvea:
\(f(x)=y\Leftrightarrow f^{-1}(y)=x\)
Olkoon \(f(x)=x^3+1\). Määritä käänteisfunktion lauseke \(f^{-1}(x)\).
Piirrä koordinaatistoon kuvaajat \(y=f(x)\), \(y=f^{-1}(x)\) ja \(y=x\). Mitä huomaat?
\(f^{-1}(x)=\sqrt[3]{x-1}\)
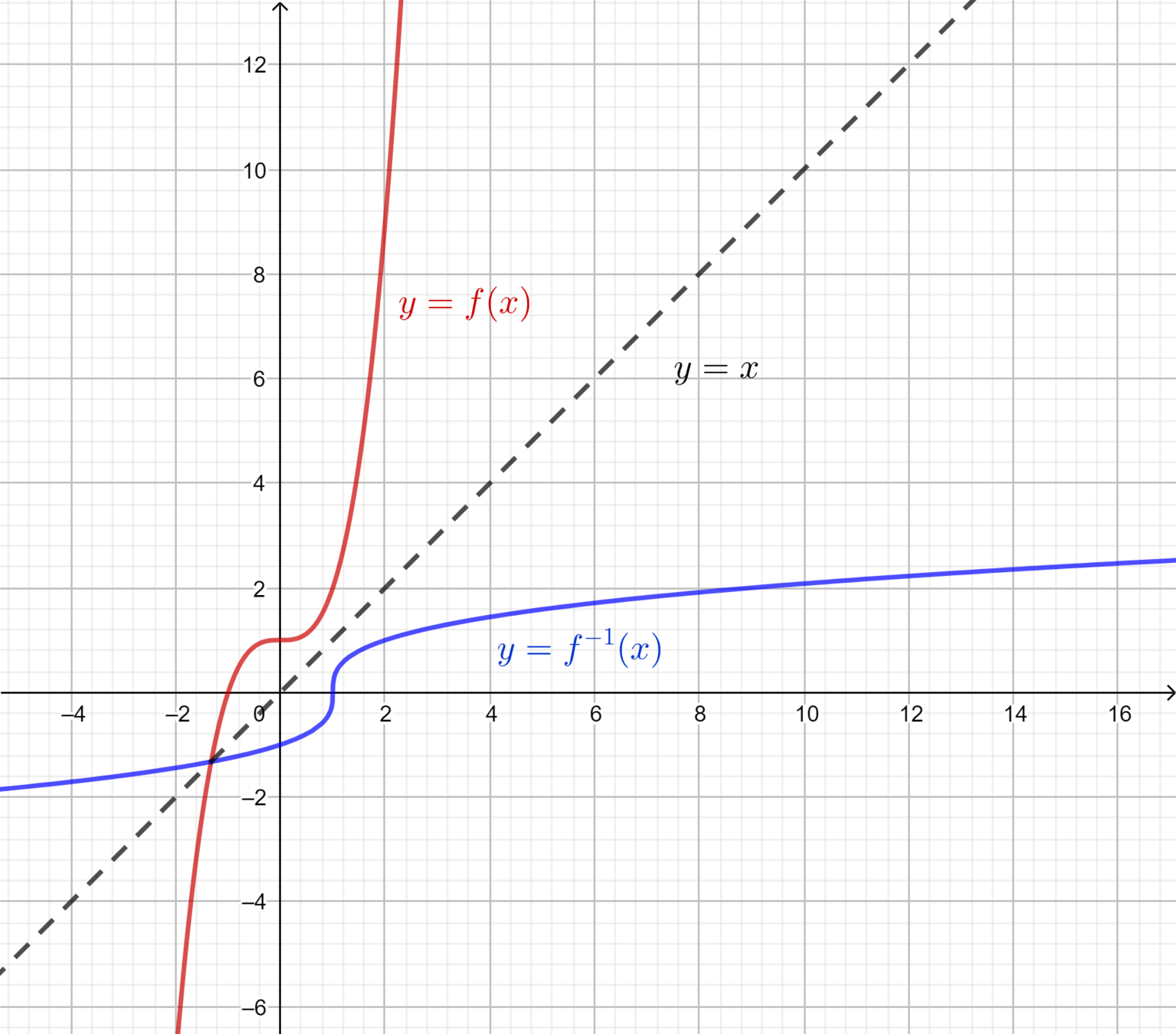
Käänteisfunktion kuvaaja on funktion kuvaajan peilikuva suoran \(y=x\) suhteen
Käänteisfunktion kuvaajan saa myös suoraan kirjoittamalla \(x=f(y)\)
\(f(x)=y\Leftrightarrow f^{-1}(y)=x\)
Käänteisfunktioiden ominaisuuksia:
- \(f\) on funktion \(g\) käänteisfunktio, jos ja vain jos \(g\) on funktion \(f\) käänteisfunktio
\[f=g^{-1}\Leftrightarrow g=f^{-1}\] - Käänteisfunktion käänteisfunktio on funktio itse
\[(f^{-1})^{-1}=f\] - Funktio ja käänteisfunktio "kumoavat" toisensa
\[f(f^{-1}(x))=x\]
\[f^{-1}(f(x))=x\]
\(f(x)=y\Leftrightarrow f^{-1}(y)=x\)
Esim olk. \(g=f^{-1}\) ja \(g(1)=2\).
Määritä \(f(2)\), \(f(g(3))\) ja \((f^{-1})^{-1}(2)\)
- Koska \(f\) on myös funktion \(g\) käänteisfunktio, niin \(f(2)=1\).
- \(f(g(3))=g^{-1}(g(3))=3\)
- \((f^{-1})^{-1}(2)=f(2)=1\)
\(f(x)=y\Leftrightarrow f^{-1}(y)=x\)
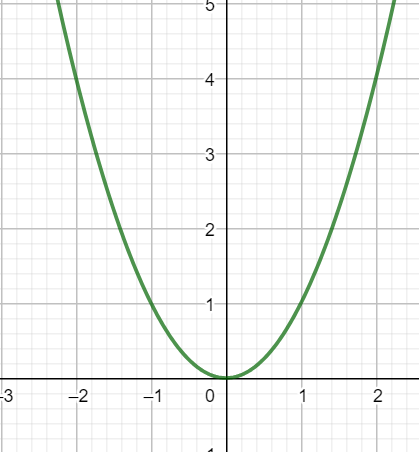
Onko funktiolla \(f:\mathbb{R}\to\mathbb{R}\), \(f(x)=x^2\) käänteisfunktiota?
Yritetään ratkaista käänteisfunktio:
\(f(x)=y\)
\(x^2=y\)
\(x=\pm\sqrt{y}\)
Käänteisfunktion pitäisi siis olla \(f^{-1}(x)=\sqrt{x}\) tai \(f^{-1}(x)=-\sqrt{x}\). Funktion määritelmän täytyy kuitenkin olla yksikäsitteinen: funktio voi saada yhdessä kohtaa vain yhden arvon. Siis käänteisfunktiota ei ole olemassa.
\(f(x)=y\Leftrightarrow f^{-1}(y)=x\)
Onko funktiolla \(f:[0,\infty[\to\mathbb{R}\), \(f(x)=x^2\) käänteisfunktiota?
\(\stackrel{+}{(-)}\)
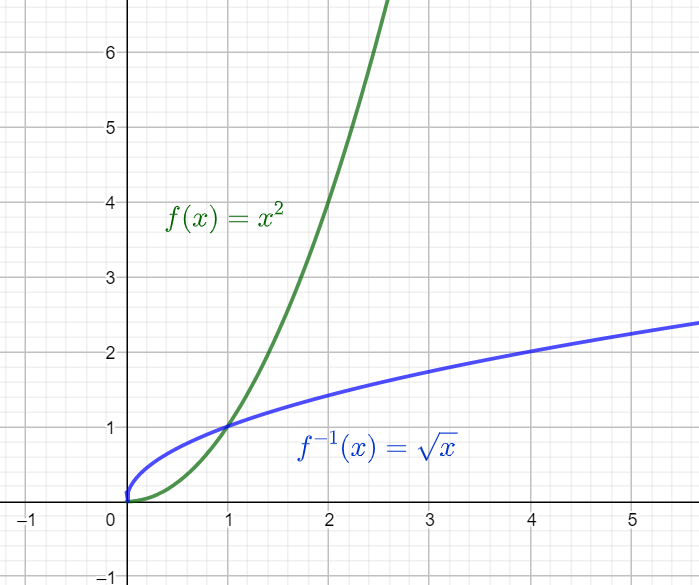
\(f(x)=y\)
\(x^2=y\)
\(x= \sqrt{y}\)
Käänteisfunktio on \(f^{-1}(x)=\sqrt{x}\)
Huom! Käänteisfunktion määrittelyjoukko on alkup. funktion arvojoukko, ja arvojoukko alkup. funktion määrittelyjoukko.
Määrittelyehto: \(x\geq 0\)
Yritetään ratkaista käänteisfunktio:
Lause Aidosti monotonisella funktiolla on käänteisfunktio.
Käänteisfunktion olemassaolon voi osoittaa ratkaisemalla käänteisfunktion.
Käänteisfunktion olemassaolemattomuuden osoittamiseksi riittää löytää myös vastaesimerkki, jolla funktio saa saman arvon kahdessa kohtaa.
Esim funktiolla \(f:\mathbb{R}\to\mathbb{R}\), \(f(x)=x^2\) ei ole käänteisfunktiota, koska \(f(-1)=1=f(1)\)
Myös seuraavasta lauseesta on olemassaolon tutkimiseksi apua:
Huom. käänteinen ei päde: funktiolla voi olla käänteisfunktio, vaikka se ei olisi aidosti monotoninen (ks. johdantoesim.)
Osoita, että funktiolla \(f(x)=x^{101}+x^{99}+x\) on käänteisfunktio
Yhtälön \(f(x)=y\) ratkaiseminen muuttujan \(x\) suhteen ei onnistu edes laskimelta
Derivoidaan \(f(x)\)
\(f'(x)=101x^{100}+99x^{98}+1\)
\(\underbrace{ }_{\geq 0}\)
\(\underbrace{ }_{\geq 0}\)
\(\geq 0 + 0 + 1=1>0\)
Koska \(f'(x)>0\) kaikilla \(x\), funktio \(f\) on aidosti kasvava, joten sillä on käänteisfunktio.
04 Käänteisfunktio
By Timo Pelkola
04 Käänteisfunktio
- 34



