Korkeammat juuret
Epänegatiivisen luvun \(a\) neliöjuuri \(\sqrt{a}\) on se epänegatiivinen luku, jonka neliö eli toinen potenssi on luku \(a\)
Ts. \(\sqrt{a}=b\), kun
- \(b\geq 0\)
- \(b^2=a\)
Esim. \(\sqrt{9}=3\), koska \(3 \geq 0\) ja \(3^2=9\)
Huom! Toisin kuin neliöjuuren, kuutiojuuren voi ottaa myös negatiivisesta luvusta.
\(\sqrt[3]{-8}=-2\), koska \((-2)^3=-8\)
Luvun \(a\) kuutiojuuri \(\sqrt[3]{a}\) on se luku, jonka kuutio eli kolmas potenssi on \(a\)
Eli \(\sqrt[3]{a}=b\), kun \(b^3=a\)
Määritelmän voi yleistää myös muille asteluvuille. Parilliset juuret käyttäytyvät kuin neliöjuuret, ja parittomat kuin kuutiojuuret
Kun \(n\) on parillinen:
Epänegatiivisen luvun \(a\) \(n\).:s juuri \(\sqrt[n]{a}\) on se epänegatiivinen luku, jonka \(n.\):s potenssi on luku \(a\)
Ts. \(\sqrt[n]{a}=b\), kun
- \(b\geq 0\)
- \(b^n=a\)
Esim. \(\sqrt[4]{16}=2\), koska \(2 \geq 0\) ja \(2^4=16\)
Määritelmän voi yleistää myös muille asteluvuille. Parilliset juuret käyttäytyvät kuin neliöjuuret, ja parittomat kuin kuutiojuuret
Kun \(n\) on pariton
Luvun \(a\) \(n\).:s juuri \(\sqrt[n]{a}\) on se luku, jonka \(n.\):s potenssi on luku \(a\)
Ts. \(\sqrt[n]{a}=b\), kun \(b^n=a\)
Esim. \(\sqrt[5]{-32}=-2\), koska \((-2)^5=-32\)
Jo opitut juurten laskusäännöt (1, 3, 5) toimivat sellaisenaan


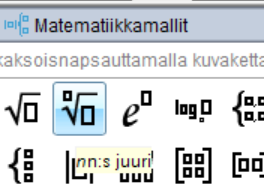
Nspirestä löytyy oma painikkeensa yleiselle juurelle.
Juuren likiarvon saa painamalla ctrl+enter.
Tarkoilla arvoilla laskiessa nspire usein sieventää juurilausekkeen eri muotoon.
Speedcrunchissa ei ole yleisille juurille omaa komentoa, vaan ne pitää laskea murtopotenssina. Esim. neljäs juuri lasketaan korottamalla luku potenssiin \(\dfrac{1}{4}\). Huom. sulkeet!
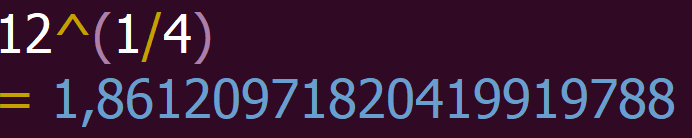
07 Korkeammat juuret
By Timo Pelkola
07 Korkeammat juuret
- 48



