Koron korko
Kertausta:
Jos korkoaika on korkeintaan yksi korkokausi (usein vuosi), niin korko maksetaan vain kerran, eli sen voi laskea yksinkertaisen koron kaavalla

Tilille, jonka nettokorko kanta on 1,2% talletetaan 1000€. Paljonko rahaa tilillä on vuoden kuluttua?
Koska korkoa kertyy korkeintaan yhden korkokauden ajalta, voidaan kertynyt korko laskea yksinkertaisen koron kaavalla \(r=kit\)
\(r=1000€\cdot0{,}012\cdot1=12€\)
Kasvanut pääoma on siis \(K_1=k+r=1000€+12€=1012€\)
Kertausta:
Toinen tapa olisi ollut laskea tämä korkotekijän
\(q=100\%+1{,}2\%=101{,}2\%=1{,}012\) avulla
\(K_1=k\cdot q = 1000€\cdot1{,}012=1012€\)
Tilille, jonka nettokorko kanta on 1,2% talletetaan 1000€. Paljonko rahaa tilillä on vuoden kuluttua?
Entä mikä tilanne on toisen vuoden jälkeen?
Toisena vuotena korkoa maksetaan myös ensimmäisenä vuotena kertyneelle korolle, eli ns. koron korkoa.
\(K_1=k\cdot q = 1000€\cdot1{,}012=1012€\)
Tilin saldon kahden vuoden kuluttua saadaan siis kertomalla korkokertoimella \(q\) kahdesti, eli sen toisella potenssilla \(q^2\)
\(K_2=k\cdot q^2=1000€\cdot1{,}012^2\approx 1024{,}14€\)
N:n vuoden kuluttua tilillä on siis
\(K_n=k\cdot q^n\)

Koron koron kaava MAOLissa. Huom. äskeisen 1,2%:n korkoa vastaavan korkokertoimen voi laskea myös
\(q=1+\dfrac{1{,}2}{100}=1{,}012\)


Jos korkoaika alle korkokausi (vuosi):
Jos korkoaika useampi kokonainen korkokausi (vuosi):
Huom. tässä kaavassa lasketaan vain koron suuruus
Huom. tässä kaavassa lasketaan suoraan kasvanut pääoma
Samassa laskussa voi tarvita molempia, jos tehdään esim. kuukausittaisi talletuksia tai korkoaika on esim. 5 vuotta ja 3 kk.
Jokaista talletusta pitää tarkistella erikseen, koska vain ensimmäinen talletuksista ehtii olla kasvamassa korkoa kokonaiset viisi vuotta!
Ensimmäinen talletus (korkoa kertyy viisi vuotta):
\(K_5=100\cdot 1{,}012^5\)
Toinen talletus (korkoa kertyy neljä vuotta):
\(K_4=100\cdot 1{,}012^4\)
....
Viides talletus (korkoa kertyy vuosi)
\(K_1=100\cdot 1{,}012^1\)
Kuudes talletus (korkoa ei ehdi kertyä)
\(K_0=100\cdot1{,}012^0\)
Tilille, jonka nettokorkokanta on 1,2%, talletetaan joka vuoden ensimmäinen päivä 100€. Paljonko tilillä on rahaa viiden vuoden jälkeen vuoden ensimmäisenä päivänä?
Tapa 1: Taulukkolaskin
Tilille, jonka nettokorkokanta on 1,2%, talletetaan joka vuoden ensimmäinen päivä 100€. Paljonko tilillä on rahaa viiden vuoden jälkeen vuoden ensimmäisenä päivänä?
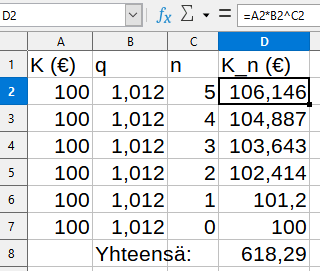
Ensimmäinen talletus (korkoa kertyy viisi vuotta):
\(K_5=100\cdot 1{,}012^5\)
...
Kuudes talletus (korkoa ei ehdi kertyä)
\(K_0=100\)
Luvut \(K_n\) muodostavat geometrisen jonon, jonka ensimmäinen jäsen on 100€ ja suhdeluku \(q=1{,}012\).
Käytetään geometrisen summan kaavaa.
Koska lukuja on 6, niin \(n=6\).
Tapa 2 (geometrinen summa):
Tilille, jonka nettokorkokanta on 1,2%, talletetaan joka vuoden ensimmäinen päivä 100€. Paljonko tilillä on rahaa viiden vuoden jälkeen vuoden ensimmäisenä päivänä?
Ensimmäinen talletus (korkoa kertyy viisi vuotta):
\(K_5=100\cdot 1{,}012^5\)
...
Kuudes talletus (korkoa ei ehdi kertyä)
\(K_0=100\)
\(S_{n}=\dfrac{a_1(1-q^n)}{1-q}\)
\(a_1=100\), \(q=1{,}012\), \(n=6\)
\(S_{6}=\dfrac{100\cdot(1-1{,}012^6)}{1-1{,}012}\approx 618{,}29€\)
Tilille, jonka nettokorkokanta on 1,2%, talletetaan joka vuoden ensimmäinen päivä 100€. Paljonko tilillä on rahaa viiden vuoden jälkeen vuoden ensimmäisenä päivänä?
Tarkastellaan yksittäistä vuotta yksinkertaisen koron avulla.
Tammikuun talletus ehtii kasvaa koko vuoden, mutta joulukuun talletus vain yhden kuukauden korkoa. Talletukset yhden vuoden aikana kertyvine korkoineen on 241,56€
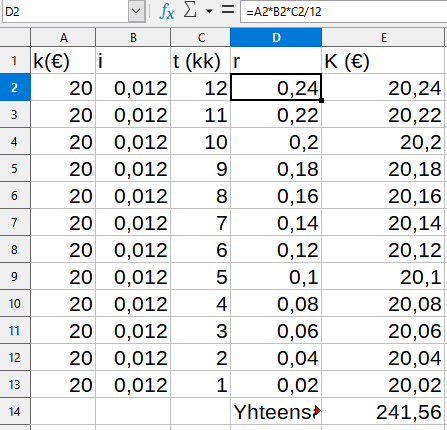
Tilille, jonka nettokorkokanta on 1,2%, talletetaan viiden vuoden ajan joka kuukauden ensimmäinen päivä 20€. Paljonko tilillä on rahaa viiden vuoden jälkeen vuoden ensimmäisenä päivänä?
Tilille, jonka nettokorkokanta on 1,2%, talletetaan viiden vuoden ajan joka kuukauden ensimmäinen päivä 20€. Paljonko tilillä on rahaa viiden vuoden jälkeen vuoden ensimmäisenä päivänä?
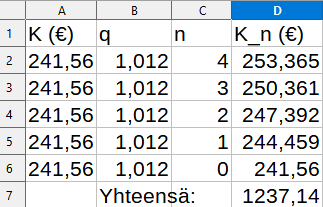
Ensimmäisen vuoden talletukset kasvavat korolle korkoa seuraavat neljä vuotta.
Toisen vuoden talletukset kasvavat korolle korkoa kolme vuotta jne.
Viidennen vuoden talletukset eivät ehdi kasvaa korolle korkoa, vaan niille maksetaan vain yksinkertainen korko.
Tilille, jonka nettokorkokanta on 1,2%, talletetaan viiden vuoden ajan joka kuukauden ensimmäinen päivä 20€. Paljonko tilillä on rahaa viiden vuoden jälkeen vuoden ensimmäisenä päivänä?
03 Koron korko
By Timo Pelkola
03 Koron korko
- 543



