Osittaisderivaatta
Yhden muuttujan funktion \(f(x)\) derivaatta \(f'(a)\) kertoo, kuinka nopeasti funktion arvo \(f(x)\) muuttuu, kun \(x\) muuttuu kohdan \(x=a\) ympäristössä.
Geometrisesti derivaatta on sama, kuin kohtaan \(x=a\) piirretyn tangentin kulmakerroin.
Kahden muuttujan funktiossa joudumme tarkastelemaan erikseen, kuinka nopeasti funktion \(f(x,y)\) arvo muuttuu, kun toisen muuttujan arvo muuttuu ja toisen arvo pysyy vakiona.
Näin tarkastelemalla saamme funktion \(f(x,y)\) osittaisderivaatat \(\partial{x}f(x,y)\) ja \(\partial{y}f(x,y)\)
\(\partial{x}f(x,y)=\mathrm{D}_{x}f(x,y)\)
\(\partial{y}f(x,y)=\mathrm{D}_{y}f(x,y)\)
Osittaisderivaattafunktio muuttujan \(x\) suhteen saadaan derivoimalla funktio muuttujan \(x\) suhteen, osittaisderivaattafunktio muutujan \(y\) suhteen vastaavasti derivoimalla funktio \(y\):n suhteen
Olk. \(f(x,y)=3x^5+\sin y+2xy\).
Määritä osittaisderivaattafunktiot ja näiden arvot pisteessä \((1,\pi)\).
Kun derivoidaan \(f(x,y)\) \(x\):n suhteen, \(y\) ajatellaan vakiona. Vakiotermin derivaatta on 0, mutta vakiokerroin otetaan derivaataan eteen.
\(\partial{x}f(x,y)=\mathrm{D}_x3x^5 + \mathrm{D}_x\sin y+\mathrm{D}_x2xy\)
\(=3\mathrm{D}_xx^5 + 0+2y\mathrm{D}_xx\)
\(=3\cdot 5x^4 + 2y\cdot 1\)
\(=15x^4 + 2y\)
Vastaavasti
\(\partial{y}f(x,y)=\mathrm{D}_y3x^5 + \mathrm{D}_y\sin y+\mathrm{D}_y2xy\)
\(=0 + \cos y + 2x\mathrm{D}_yy\)
\(=\cos y + 2x\cdot 1 = \cos y + 2x\)
Kun \((x,y)=(1,\pi)\):
\( 15x^4+2y\\=15\cdot1^4+2\pi\\=2\pi+15\)
Kun \((x,y)=(1,\pi)\):
\( \cos y + 2x\\=\cos \pi + 2\cdot 1\\= -1 + 2 = 1\)
Nspiressä:
(Muistutus: jos kirjoittaisi vain "xy", nspire tulkitsisi tämän muuttujaksi nimeltä "xy", ei kertolaskuksi \(x\cdot y\))

Geometrisesti osittaisderivaatta \(\partial{x}f(x,y)\) kohdassa \((a,b)\) on tason \(y=b\) ja kuvaajan \(z=f(x,y)\):n leikkauskäyrän kohtaan \(x=a\) piirretyn tangentin kulmakerroin.
Vastaava pätee myös muuttujan \(y\) suhteen.
Yhden muuttujan funktion derivaatan nollakohdat ovat joko funktion ääriarvo- tai terassikohtia
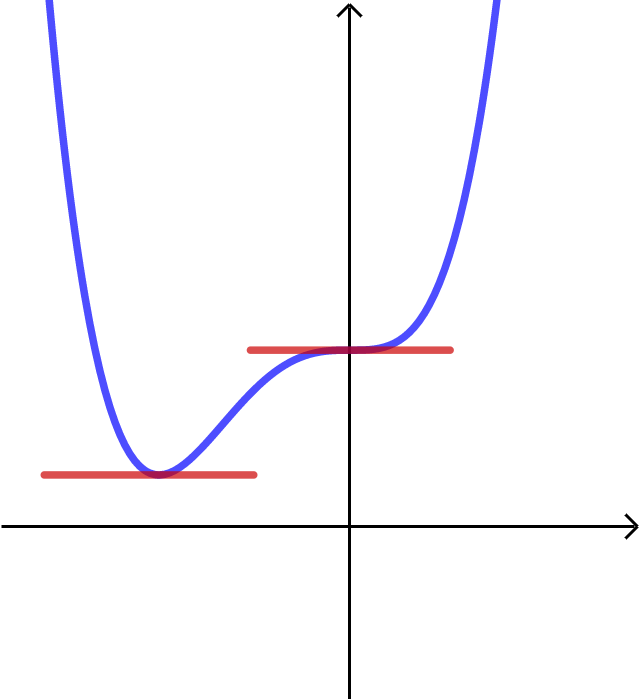
Vastaavalla tavalla kahden muuttujan funktioissa piste \((a,b)\) on funktion \(f(x,y)\) ääriarvokohta tai satulapiste, jos \((x,y)=(a,b)\) on yhtälöparin
\(\begin{cases}\partial{x}f(x,y)=0\\\partial{y}f(x,y)=0\end{cases}\)
ratkaisu.
Ääriarvokohtia ja satulapisteitä kutsutaan kriittisiksi pisteiksi. Näiden laatu, eli ovatko ne ääriarvokohtia vai satulapisteitä, selviää esim. kuvaajasta.
Määritä funktion \(f(x,y)=-x^3+x^2+y^2\) kriittiset pisteet ja niiden laatu
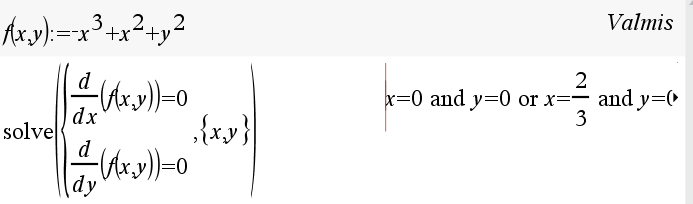
Kriittiset pisteet ovat \((0,0)\) ja \((\dfrac{2}{3},0)\)
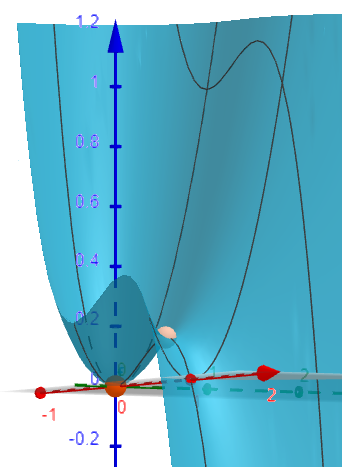
Koska pisteen \((0,0)\) ympäristössä funktion arvot kasvavat, kyseessä on minimikohta.
Koska pisteen \((\dfrac{2}{3},0)\) ympäristössä funktion arvot sekä kasvavat että pienenevät suunnasta riippuen, kyseessä on satulapiste.
- Kahden muuttujan funktion kasvunopeus riippuu siitä, mihin suuntaan \(xy\)-tasossa liikutaan.
- Kun liikutaan x-akselin suuntaisesti eli vektorin \(\bar{i}\) suuntaan, kasvunopeus voidaan selvittää osittaiderivaatan \(\partial{x}f(x,y)\) avulla.
- Kun liikutaan y-akselin suuntaisesti eli vektorin \(\bar{j}\) suuntaan, kasvunopeus voidaan selvittää osittaiderivaatan \(\partial{y}f(x,y)\) avulla.
- Funktion arvot kasvavat nopeiten, kun liikutaan gradientin eli vektorin \(\nabla f(x,y)=\partial{x}f(x,y)\bar{i}+\partial{y}f(x,y)\bar{j}\) suuntaisesti.
- Funktion arvot pienenevät nopeiten, kun liikutan gradientin vastavektorin \(-\nabla f(x,y)\) suuntaan
- Suurin kasvunopeus on gradienttivektorin pituus \(|\nabla f(x,y)|\)
Intuitiivisesti gradientti kertoo, mihin suuntaan xy-tasossa vuorikiipeilijän pitäisi kiivetä, jotta nousisi mahdollisimman nopeasti

Määritä funktion \(f(x,y)=x^2+y^2\) suurin kasvunopeus kohdassa \((1,3)\)
\(\nabla f(x,y)=\partial_{x}f(x,y)\bar{i}+\partial_{y}f(x,y)\bar{j}\)
\(=2x\bar{i}+2y\bar{j}\)
Kun \((x,y)=(1,3)\),
\(|\nabla f(x,y)|=|(2\cdot 1) \bar{i}+(2\cdot 3)\bar{j}|\)
\( = |2\bar{i} + 6\bar{j}|\)
\( = \sqrt{2^2 + 6^2}=\sqrt{4+36}=\sqrt{40}=2\sqrt{10}\)
16 Osittaisderivaatta
By Timo Pelkola
16 Osittaisderivaatta
- 38



