Pisteen etäisyys suorasta
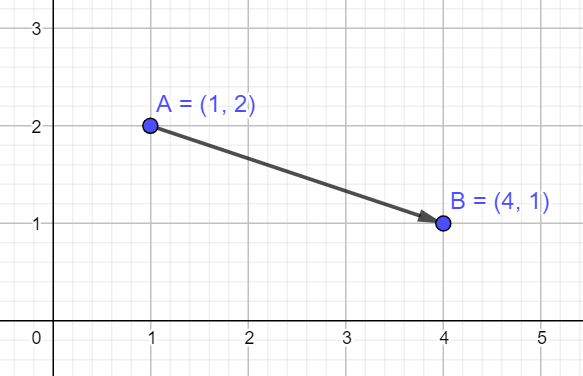
Kahden pisteen välinen etäisyys saadaan laskettua niiden välisen vektorin pituutena
\(\overline{AB}=(4-1)\bar{i}+(1-2)\bar{j}=3\bar{i}-\bar{j}\)
\(|\overline{AB}|=\sqrt{3^2+(-1)^2}=\sqrt{10}\approx 3{,}2\)
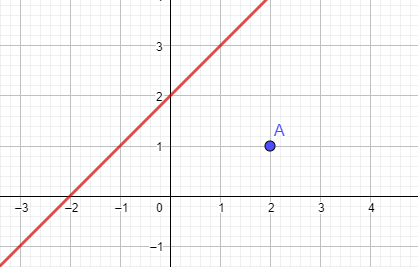
- Pisteen ja suoran etäisyyttä laskiessa lasketaan todelisuudessa pisteen ja jonkin suoran pisteen välistä etäisyyttä
- Jos voisi valita minkä tahansa pisteen suoralta, etäisyys voisi olla kuinka suuri tahansa
- Etäisyys ei kuitenkaan voi olla kuinka pieni tahansa
- Valitaan se suoran piste, jolla etäisyys on mahdollisimman pieni, eli kohtisuora etäisyys
- Valittu suoran piste on siis tutkittavasta pisteestä suoralle piirretyn normaalivektorin päätepiste
- Pisteen etäisyys suorasta voidaan laskea tämän normaalivektorin pituutena
◻
●
●
●
- Normaalivektori \(\bar{n}\) voidaan ajatella tarkisteltavan pisteen \(A\) ja suoran parametrisoidun yleisen pisteen \(P\) välisenä vektorina \(\overline{AP}\). Parametrin arvo ratkeaa yhtälöstä \(\bar{s}\cdot\bar{n}=0\)
\(P\)
\(\bar{s}\)
\(\bar{n}\)
Laske pisteen \(A=(1,2,3)\) etäisyys suorasta \(\begin{cases}x=t\\y=t\\z=t\end{cases}, (t\in\mathbb{R})\)
Suoran suuntavektori: \(\bar{s}=\bar{i}+\bar{j}+\bar{k}\)
Suoran piste: \(P=(x,y,z)=(t,t,t)\)
Normaalivektori: \(\bar{n}=\overline{AP}=(t-1)\bar{i}+(t-2)\bar{j}+(t-3)\bar{k}\)
Kohtisuoruusehto: \(\overline{n}\cdot\bar{s}=0\)
\((t-1)\cdot 1 + (t-2)\cdot 1 + (t-3)\cdot 1 = 0\)
\(t-1 + t-2 + t-3 = 0\)
\(3t = 6\)
\(t = 2\)
Siis:
\(\bar{n}=(2-1)\bar{i}+(2-2)\bar{j}+(2-3)\bar{k}\\~~~~=\bar{i}-\bar{k}\)
\(|\bar{n}|=\sqrt{1^2+(-1)^2}=\sqrt{2}\)
V: \(\sqrt{2}\)
◻
●
\(P\)
\(\bar{s}\)
\(\bar{n}\)
Mallikuva:
15 Pisteen etäisyys suorasta
By Timo Pelkola
