Suhteellisen osuuden luottamusväli
Tutkimus toteutettiin 4.–9.10.2023, ja vastaajia oli 1 368. Virhemarginaali on max. ±2,2 prosenttiyksikköä.
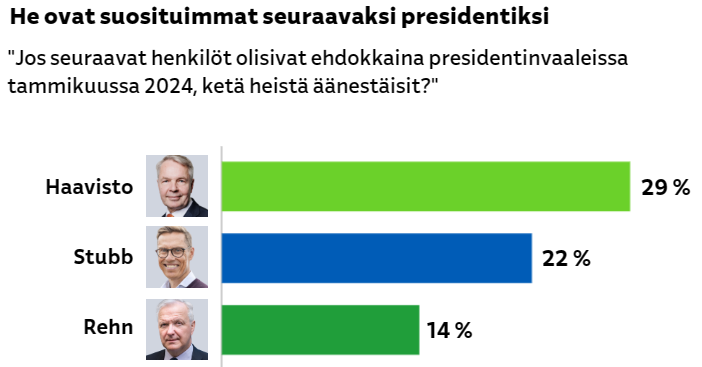
Tutkimus toteutettiin 4.–9.10.2023, ja vastaajia oli 1 368. Virhemarginaali on max. ±2,2 prosenttiyksikköä.
Miten virhemarginaali ±2,2%-yks. on laskettu?
Jokaisen ehdokkaan kannatusta varten voisi laskea oman virhemarginaalin, mutta usein yksinkertaisuuden vuoksi vain suurin näistä ilmoitetaan. Suurin virhemarginaali on suurimmalla suhteellisella osuudella, eli tässä tapauksessa suosituimmalla ehdokkaalla.
Ellei muuta ole sanottu, käytetään yleensä 95%:n luottamusväliä.


Tutkimus toteutettiin 4.–9.10.2023, ja vastaajia oli 1 368. Virhemarginaali on max. ±2,2 prosenttiyksikköä.
Miten virhemarginaali ±2,2%-yks. on laskettu?


MAOL:

Tutkimus toteutettiin 4.–9.10.2023, ja vastaajia oli 1 368. Virhemarginaali on max. ±2,2 prosenttiyksikköä.
Miten virhemarginaali ±2,2%-yks. on laskettu?
\(\left[ \hat{p}-1,96s;\ \hat{p}+1,96s \right]\)
\(s=\sqrt{\dfrac{\hat{p}(1-\hat{p})}{n}}\)
\(\hat p=29\%=0{,}29\)
\(n=1368\)
\(=\sqrt{\dfrac{0{,}29(1-0{,}29)}{1368}}= 0{,}012268...\)
95%:n luottamusväliä vastaava virhemarginaali on \(1{,}96s=1{,}96\cdot 0{,}012268...\approx 0{,}024=2{,}4\)%-yks.
0,2%-yks. ero laskuissa selittynee sillä, että tutkimuksen toteuttaja on saanut pienennettyä virhemarginaalia kyselyyn muuta tietoa yhdistävillä "korjauskertoimilla"

Tutkimus toteutettiin 4.–9.10.2023, ja vastaajia oli 1 368. Virhemarginaali on max. ±2,2 prosenttiyksikköä.
Lasketaan vielä Stubbin kannatuksen virhemarginaali
\(\left[ \hat{p}-1,96s;\ \hat{p}+1,96s \right]\)
\(s=\sqrt{\dfrac{\hat{p}(1-\hat{p})}{n}}\)
\(\hat p=22\%=0{,}22\)
\(n=1368\)
\(=\sqrt{\dfrac{0{,}29(1-0{,}29)}{1368}}= 0{,}01068...\)
95%:n luottamusväliä vastaava virhemarginaali on \(1{,}96s=1{,}96\cdot 0{,}01068...\approx 0{,}021=2{,}1\)%-yks.

\(\pm 2{,}4\%\)
\(\pm 2{,}1\%\)
Itse laskettuja virhemarginaaleja käyttäen Haaviston kannatus on 95%:n luottamustasolla välillä \([26{,}6\%;31{,}4\%]\) ja Stubbin \([19{,}9\%;24{,}1\%]\).
Koska Haaviston kannatus ei sisälly Stubbin kannatuksen luottamusväliin, voidaan 95% luottamustasolla sanoa, että Haaviston kannatus on Stubbia suurempi


Entä voidaanko sanoa 95%:n luottamustasolla, että Halla-ahon kannatus on suurempi kuin Anderssonin?
Lasketaan luottamusvälit Geogebralla.
Geogebraa varten tarvitaan kuitenkin prosenttiosuuksien sijaan vastaajien lukumäärä.
Kaikki vastaajat: 1368
Halla-aho: \(0{,}08\cdot 1368\approx 109\)
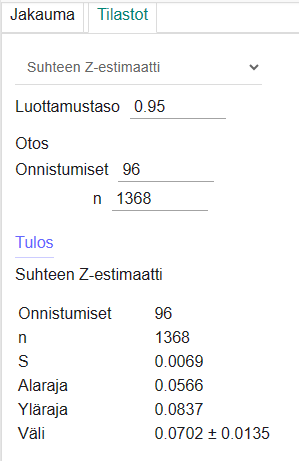
Andersson: \(0{,}07\cdot 1368\approx 96\)
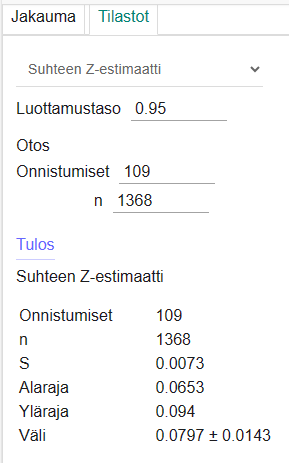
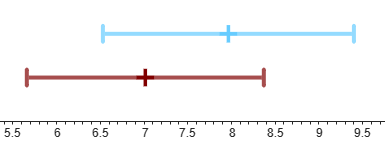
Halla-aho: \([6{,}53\%;9{,}4\%]\)
Andersson: \([5{,}66\%;8{,}37\%]\)
Koska Halla-ahon kannatus kuuluu Anderssonin kannatuksen luottamusväliin, ei voida sanoa 95%:n luottamustasolla, että Halla-ahon kannatus olisi suurempi kuin Anderssonin
09 Suhteellisen osuuden luottamusväli
By Timo Pelkola
09 Suhteellisen osuuden luottamusväli
- 305



