Suurin ja pienin arvo
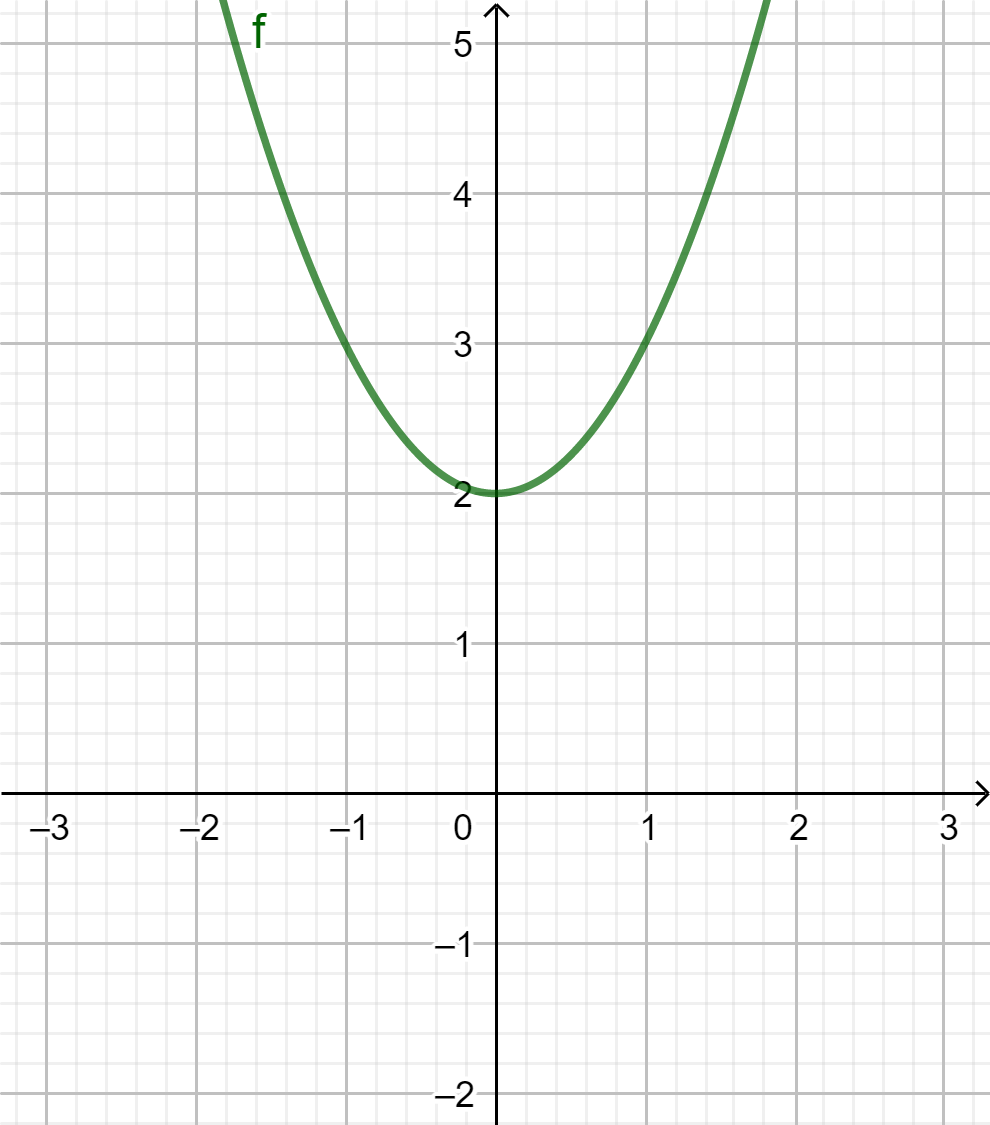
Tutki kuvaajan avulla, onko funktiolla \(f(x)=x^2+2\)
a) pienin arvo b) suurin arvo?
a) On, 2.
b) Ei. Funktio kasvaa rajatta.
Tutki kuvaajan avulla, onko funktiolla \(g(x)=x^3-3x^2+4\)
a) pienin arvo b) suurin arvo?
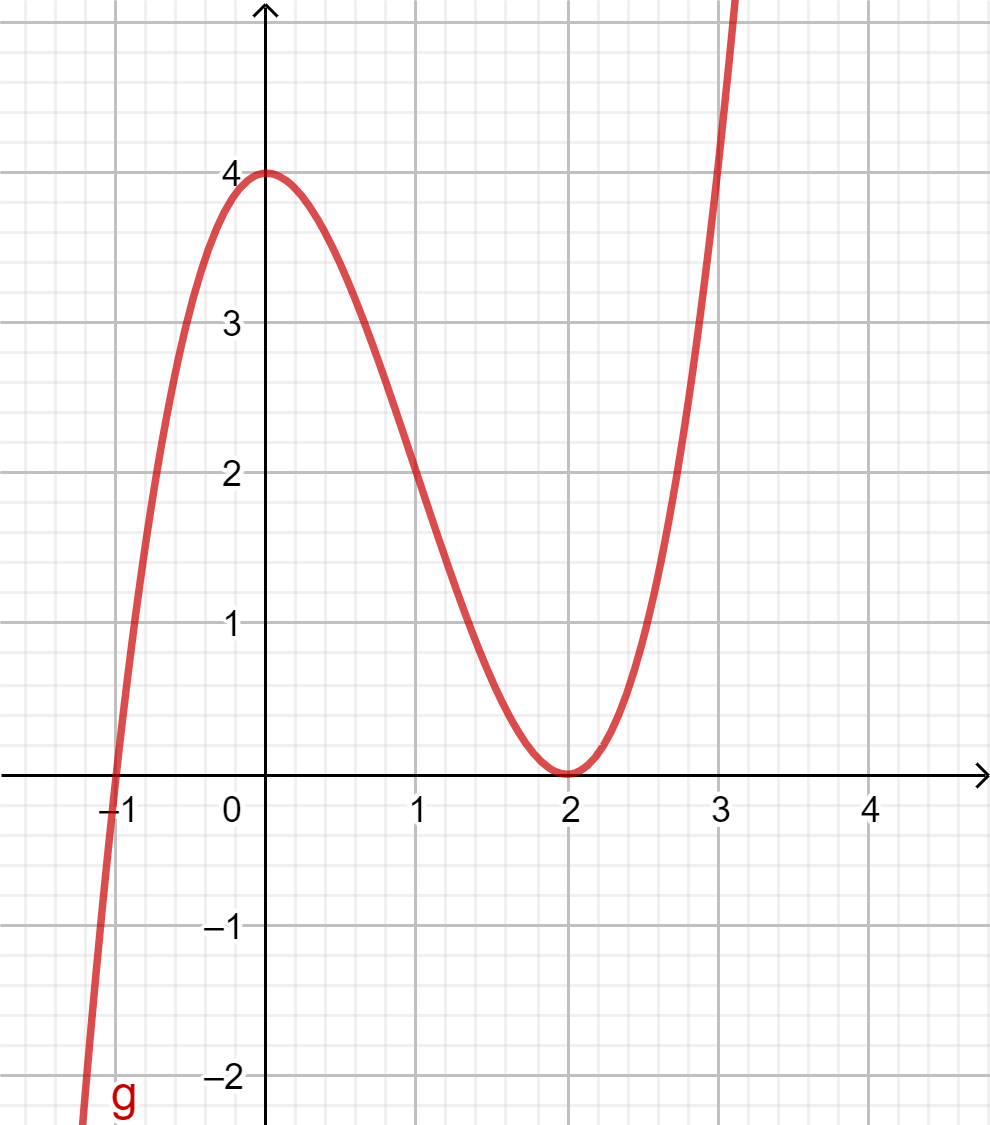
a) Ei, funktio pienenee rajatta, kun \(x\) pienenee rajatta.
b) Ei, funktio kasvaa rajatta,
kun \(x\) kasvaa rajatta.
Vaikka funktiolla \(g(x)=x^3-3x^2+4\) on sekä (paikallinen) minimiarvo että maksimiarvo, sillä ei ole pienintä eikä suurinta arvoa!

Entä, jos rajataankin tarkastelu välille \(1\leq x \leq 3\)?
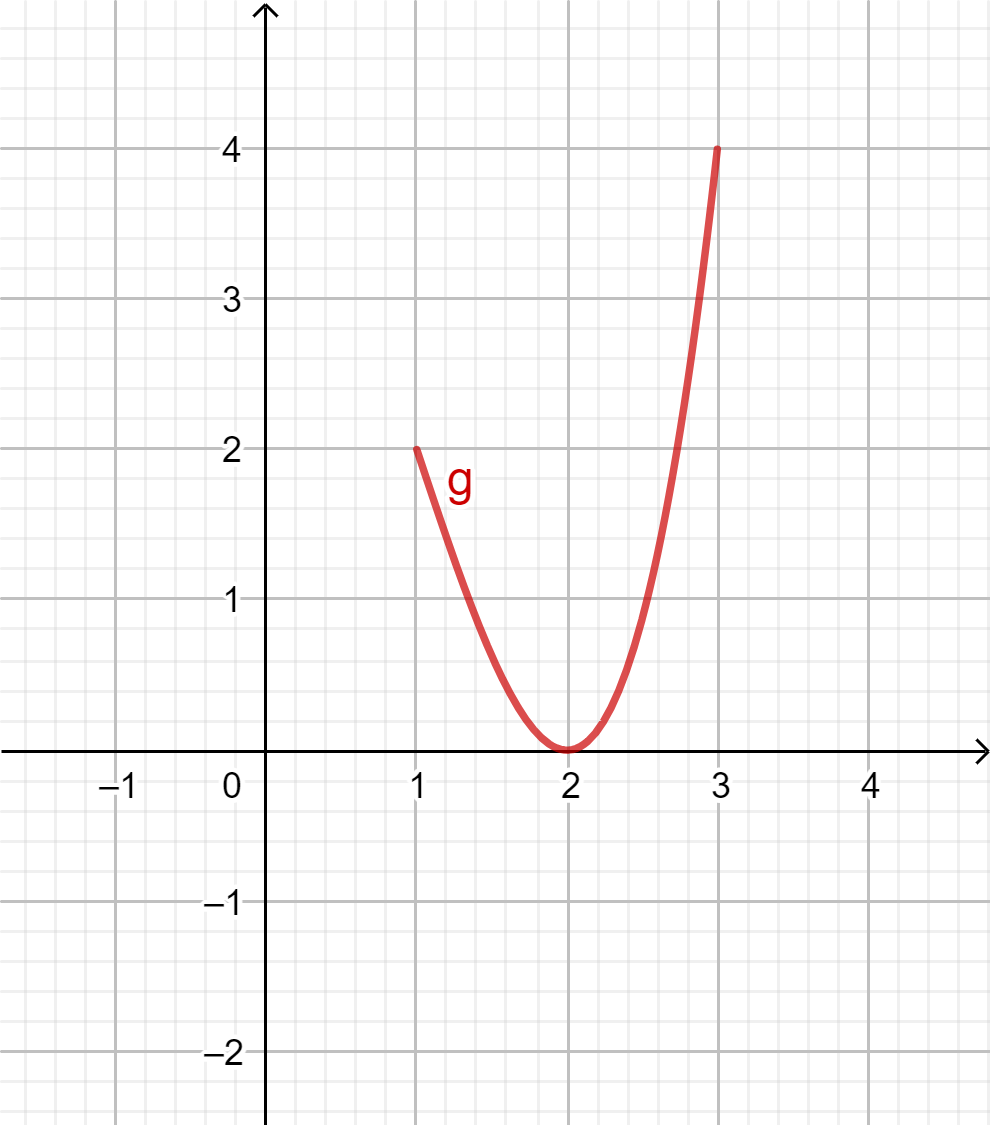
Välillä \(1\leq x \leq 3\) funktion \(g\) pienin arvo on 0 ja suurin arvo 4.
Suljetulla välillä \(a\leq x \leq b\) polynomifunktio saa aina suurimman ja pienimmän arvon. Suurin ja pienin arvo saavutetaan välin päätepisteissä tai derivaatan nollakohdissa.
suurin
pienin
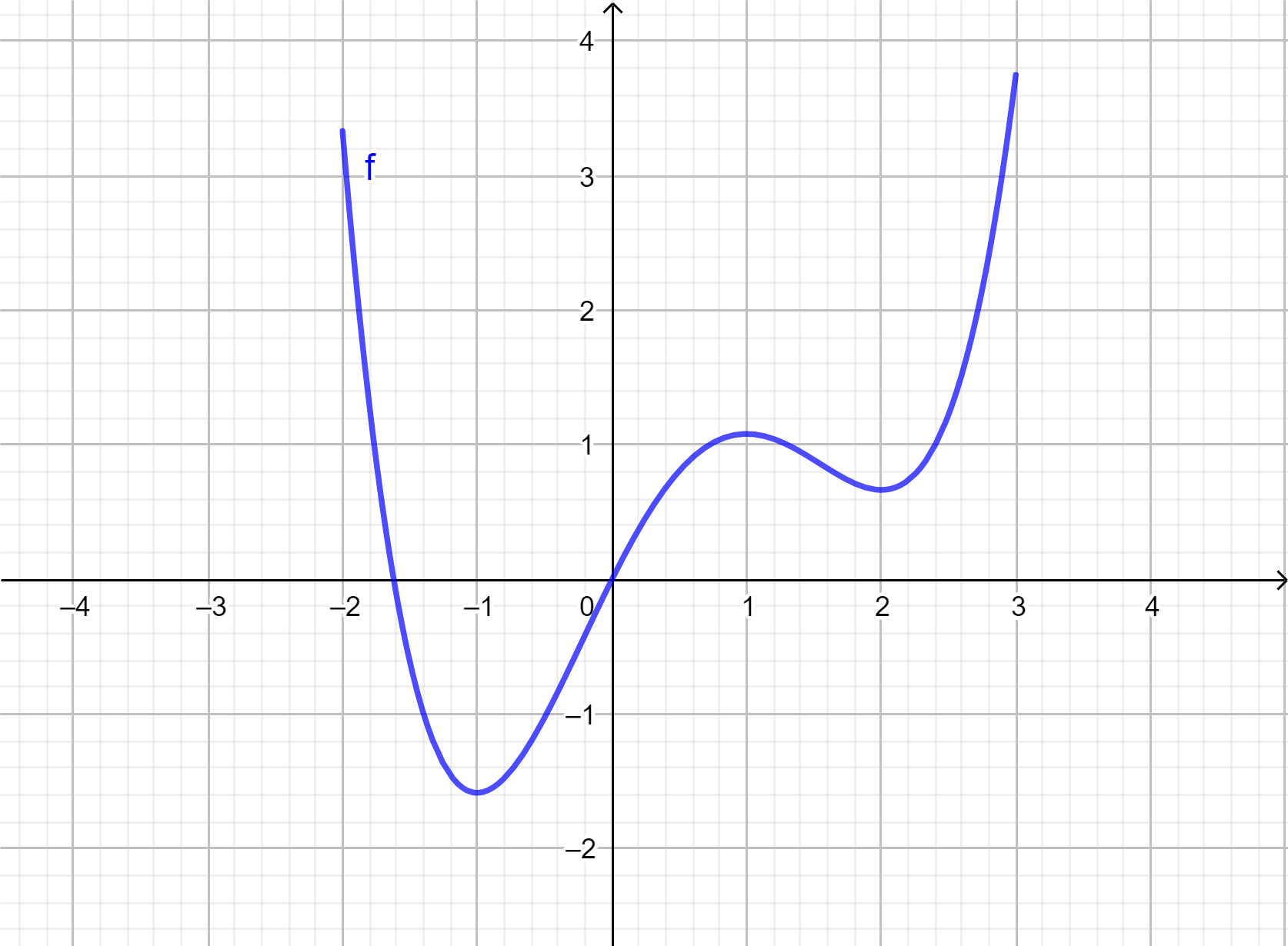
Mikä on funktion \(f(x)=x^2-2x\), jossa \(-3\leq x \leq 2\)
a) suurin b) pienin arvo?
Suljetulla välillä \(a\leq x \leq b\) polynomifunktio saa aina suurimman ja pienimmän arvon. Suurin ja pienin arvo saavutetaan välin päätepisteissä tai derivaatan nollakohdissa.
Derivoidaan funktio
\(f'(x)=2x-2\)
Ratkaistaan derivaatan nollakohdat
\(f'(x)=0\)
\(2x=2 \parallel :2\)
\(2x-2=0\)
\(x=1 \)
Lasketaan funktion arvot derivaatan nollakohdissa ja välin päätepisteissä
\(f(-3)=(-3)^2-2\cdot(-3)\)
\(f(1)=1^2-2\cdot1\)
\(f(2)=2^2-2\cdot2\)
\(=9+6=15\)
\(=1-2=-1\)
\(=4-4=0\)
(suurin)
(pienin)
V: a) 15, b) -1
Suurinta ja pienintä arvoa kutsutaan myös globaaliksi maksimiksi ja minimiksi erotuksena (paikallisesta) maksimista ja minimistä
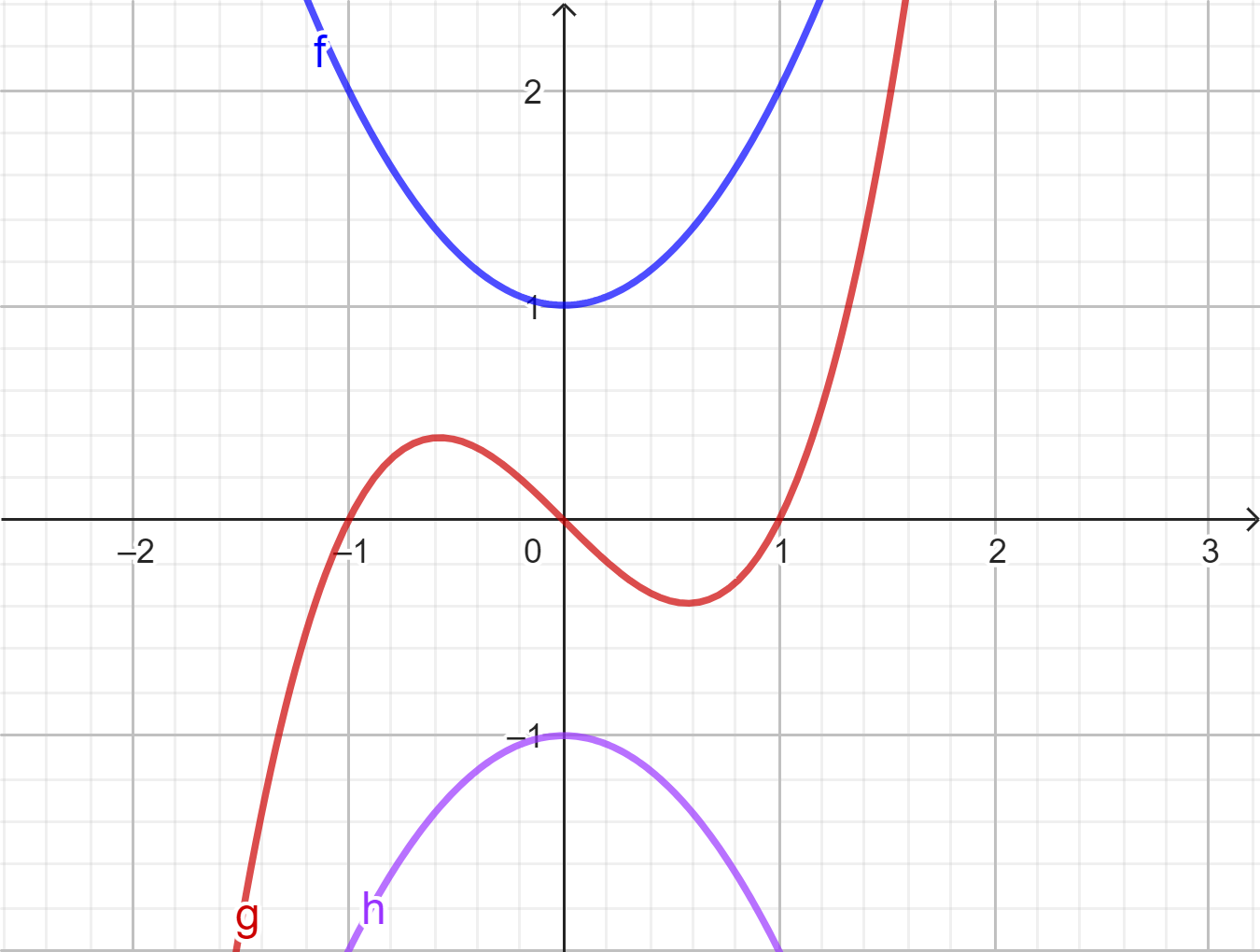
Jos funktion tarkastelua ei rajata suljetulle välille, funktion mahdolliset suurimmat ja pienimmät arvot löytyvät ääriarvokohdista. Tässä päättelyssä auttaa kulkukaavio ja tieto, että polynomifunktio aina kasvaa rajatta (\(f(x)\)), pienenee rajatta (\(h(x)\)) tai molempia (\(g(x)\)), kun \(x\) kasvaa tai pienenee rajatta.
Tutki kulkukaavion avulla, onko funktiolla \(f(x)=x^2+2\)
a) pienin arvo b) suurin arvo?
Derivoidaan funktio
\(f'(x)=2x\)
Ratkaistaan derivaatan nollakohdat
\(f'(x)=0\)
\(2x=0\parallel :2\)
\(x=0\)
Luodaan kulkukaavio
\(f'(x)\)
\(f(x)\)
0
\(f'(-1)=2\cdot(-1)=-2<0\)
-
+
\(f'(1)=2\cdot 1=2>0\)
\(\nearrow\)
\(\searrow\)
min
Testipisteet
Tutki kulkukaavion avulla, onko funktiolla \(f(x)=x^2+2\)
a) pienin arvo b) suurin arvo?
\(f'(x)\)
\(f(x)\)
0
-
+
\(\nearrow\)
\(\searrow\)
min
a) Funktio saa pienimmän arvonsa kohdassa \(x=0\), koska sen vasemmalla ja oikealla puolella funktio saa vain suurempia arvoja. Pienin arvo on siis \(f(0)=0^2+2=2\).
b) Funktiolla ei ole suurinta arvoa, koska se kasvaa rajatta, kun \(x\) kasvaa rajatta
11 Suurin ja pienin arvo
By Timo Pelkola
11 Suurin ja pienin arvo
- 19



