Neural Networks

Backward propagation

Training samples :

\left \{ (\bold{x^{(1)}},\bold{y^{(1)}}),(\bold{x^{(2)}},\bold{y^{(2)}}),...,(\bold{x^{(m)}},\bold{y^{(m)}}) \right \}
{(x(1),y(1)),(x(2),y(2)),...,(x(m),y(m))}\left \{ (\bold{x^{(1)}},\bold{y^{(1)}}),(\bold{x^{(2)}},\bold{y^{(2)}}),...,(\bold{x^{(m)}},\bold{y^{(m)}}) \right \}
\bold{x}
x\bold{x}
x_{1}
x1x_{1}
x_{2}
x2x_{2}
x_{3}
x3x_{3}

Training samples :

\left \{ (\bold{x^{(1)}},\bold{y^{(1)}}),(\bold{x^{(2)}},\bold{y^{(2)}}),...,(\bold{x^{(m)}},\bold{y^{(m)}}) \right \}
{(x(1),y(1)),(x(2),y(2)),...,(x(m),y(m))}\left \{ (\bold{x^{(1)}},\bold{y^{(1)}}),(\bold{x^{(2)}},\bold{y^{(2)}}),...,(\bold{x^{(m)}},\bold{y^{(m)}}) \right \}
\bold{ \hat{y} }
y^\bold{ \hat{y} }
\hat{y}_{1}
y^1\hat{y}_{1}
\hat{y}_{2}
y^2\hat{y}_{2}
\hat{y}_{3 }
y^3\hat{y}_{3 }
\bold{x}
x\bold{x}
x_{1}
x1x_{1}
x_{2}
x2x_{2}
x_{3}
x3x_{3}

Training samples :

\left \{ (\bold{x^{(1)}},\bold{y^{(1)}}),(\bold{x^{(2)}},\bold{y^{(2)}}),...,(\bold{x^{(m)}},\bold{y^{(m)}}) \right \}
{(x(1),y(1)),(x(2),y(2)),...,(x(m),y(m))}\left \{ (\bold{x^{(1)}},\bold{y^{(1)}}),(\bold{x^{(2)}},\bold{y^{(2)}}),...,(\bold{x^{(m)}},\bold{y^{(m)}}) \right \}
\bold{ \hat{y} }
y^\bold{ \hat{y} }
\hat{y}_{1}
y^1\hat{y}_{1}
\hat{y}_{2}
y^2\hat{y}_{2}
\hat{y}_{3 }
y^3\hat{y}_{3 }
W^{(1)}_{ij}
Wij(1)W^{(1)}_{ij}
W^{(2)}_{ij}
Wij(2)W^{(2)}_{ij}
W^{(3)}_{ij}
Wij(3)W^{(3)}_{ij}
\bold{x}
x\bold{x}
x_{1}
x1x_{1}
x_{2}
x2x_{2}
x_{3}
x3x_{3}
\bold{ \hat{y} }
y^\bold{ \hat{y} }
\hat{y}_{1}
y^1\hat{y}_{1}
\hat{y}_{2}
y^2\hat{y}_{2}
\hat{y}_{3 }
y^3\hat{y}_{3 }
W^{(1)}_{ij}
Wij(1)W^{(1)}_{ij}
W^{(2)}_{ij}
Wij(2)W^{(2)}_{ij}
W^{(3)}_{ij}
Wij(3)W^{(3)}_{ij}

Optimize the weights

W^{(l)}_{ij}
Wij(l)W^{(l)}_{ij}
\bold{ \hat{y} } \approx \bold{y}
y^≈y\bold{ \hat{y} } \approx \bold{y}

Training samples :

\left \{ (\bold{x^{(1)}},\bold{y^{(1)}}),(\bold{x^{(2)}},\bold{y^{(2)}}),...,(\bold{x^{(m)}},\bold{y^{(m)}}) \right \}
{(x(1),y(1)),(x(2),y(2)),...,(x(m),y(m))}\left \{ (\bold{x^{(1)}},\bold{y^{(1)}}),(\bold{x^{(2)}},\bold{y^{(2)}}),...,(\bold{x^{(m)}},\bold{y^{(m)}}) \right \}

Foward propagation

\bold{x}
x\bold{x}
x_{1}
x1x_{1}
x_{2}
x2x_{2}
x_{3}
x3x_{3}
\bold{x} =
x=\bold{x} =
x_{1}
x1x_{1}
x_{2}
x2x_{2}
x_{3}
x3x_{3}
\bold{ a^{(1)} }
a(1)\bold{ a^{(1)} }
\bold{x} =
x=\bold{x} =
x_{1}
x1x_{1}
x_{2}
x2x_{2}
x_{3}
x3x_{3}
\bold{ a^{(1)} }
a(1)\bold{ a^{(1)} }
W^{(1)}
W(1)W^{(1)}
\bold{x} =
x=\bold{x} =
x_{1}
x1x_{1}
x_{2}
x2x_{2}
x_{3}
x3x_{3}
\bold{ z^{(2)}}
z(2)\bold{ z^{(2)}}
\bold{ a^{(1)} }
a(1)\bold{ a^{(1)} }
W^{(1)}
W(1)W^{(1)}
\color{Green}{ \bold{ z^{(2)} }} = \bold{ W^{(1)}. \color{red}{a^{(1)}} }
z(2)=W(1).a(1)\color{Green}{ \bold{ z^{(2)} }} = \bold{ W^{(1)}. \color{red}{a^{(1)}} }
\color{Green}{z^{(2)}_{i}} =\sum_{j} W^{(1)}_{ij}. \color{Red}{a^{(1)}_{j}}
zi(2)=∑jWij(1).aj(1)\color{Green}{z^{(2)}_{i}} =\sum_{j} W^{(1)}_{ij}. \color{Red}{a^{(1)}_{j}}
\bold{x} =
x=\bold{x} =
x_{1}
x1x_{1}
x_{2}
x2x_{2}
x_{3}
x3x_{3}
\bold{ z^{(2)}}
z(2)\bold{ z^{(2)}}
\bold{ a^{(2)}}
a(2)\bold{ a^{(2)}}
\bold{ a^{(1)} }
a(1)\bold{ a^{(1)} }
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
W^{(1)}
W(1)W^{(1)}
\color{Red}{ \bold{ a^{(2)} }} = g( \bold{ \color{Green}{z^{(2)}} } )
a(2)=g(z(2))\color{Red}{ \bold{ a^{(2)} }} = g( \bold{ \color{Green}{z^{(2)}} } )
\color{Red}{a^{(2)}_{j}} =g( \color{Green}{z^{(2)}_{i}} )
aj(2)=g(zi(2))\color{Red}{a^{(2)}_{j}} =g( \color{Green}{z^{(2)}_{i}} )
\bold{x} =
x=\bold{x} =
x_{1}
x1x_{1}
x_{2}
x2x_{2}
x_{3}
x3x_{3}
\bold{ z^{(2)}}
z(2)\bold{ z^{(2)}}
\bold{ a^{(2)}}
a(2)\bold{ a^{(2)}}
\bold{ z^{(3)}}
z(3)\bold{ z^{(3)}}
\bold{ a^{(1)} }
a(1)\bold{ a^{(1)} }
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
W^{(1)}
W(1)W^{(1)}
W^{(2)}
W(2)W^{(2)}
\color{Green}{ \bold{ z^{(3)} }} = \bold{ W^{(2)}. \color{red}{a^{(2)}} }
z(3)=W(2).a(2)\color{Green}{ \bold{ z^{(3)} }} = \bold{ W^{(2)}. \color{red}{a^{(2)}} }
\color{Green}{z^{(3)}_{i}} =\sum_{j} W^{(2)}_{ij}. \color{Red}{a^{(2)}_{j}}
zi(3)=∑jWij(2).aj(2)\color{Green}{z^{(3)}_{i}} =\sum_{j} W^{(2)}_{ij}. \color{Red}{a^{(2)}_{j}}
\bold{x} =
x=\bold{x} =
x_{1}
x1x_{1}
x_{2}
x2x_{2}
x_{3}
x3x_{3}
\bold{ z^{(2)}}
z(2)\bold{ z^{(2)}}
\bold{ a^{(2)}}
a(2)\bold{ a^{(2)}}
\bold{ z^{(3)}}
z(3)\bold{ z^{(3)}}
\bold{ a^{(1)} }
a(1)\bold{ a^{(1)} }
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
W^{(1)}
W(1)W^{(1)}
W^{(2)}
W(2)W^{(2)}
\bold{ a^{(3)}}
a(3)\bold{ a^{(3)}}
\color{Red}{ \bold{ a^{(3)} }} = g( \bold{ \color{Green}{z^{(3)}} } )
a(3)=g(z(3))\color{Red}{ \bold{ a^{(3)} }} = g( \bold{ \color{Green}{z^{(3)}} } )
\color{Red}{a^{(3)}_{j}} =g( \color{Green}{z^{(3)}_{i}} )
aj(3)=g(zi(3))\color{Red}{a^{(3)}_{j}} =g( \color{Green}{z^{(3)}_{i}} )
\bold{x} =
x=\bold{x} =
x_{1}
x1x_{1}
x_{2}
x2x_{2}
x_{3}
x3x_{3}
\bold{ z^{(2)}}
z(2)\bold{ z^{(2)}}
\bold{ a^{(2)}}
a(2)\bold{ a^{(2)}}
\bold{ z^{(3)}}
z(3)\bold{ z^{(3)}}
\bold{ a^{(1)} }
a(1)\bold{ a^{(1)} }
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
W^{(1)}
W(1)W^{(1)}
W^{(2)}
W(2)W^{(2)}
\bold{ a^{(3)}}
a(3)\bold{ a^{(3)}}
\color{Red}{ \bold{ a^{(3)} }} = g( \bold{ \color{Green}{z^{(3)}} } )
a(3)=g(z(3))\color{Red}{ \bold{ a^{(3)} }} = g( \bold{ \color{Green}{z^{(3)}} } )
\color{Red}{a^{(3)}_{j}} =g( \color{Green}{z^{(3)}_{i}} )
aj(3)=g(zi(3))\color{Red}{a^{(3)}_{j}} =g( \color{Green}{z^{(3)}_{i}} )
\bold{x} =
x=\bold{x} =
x_{1}
x1x_{1}
x_{2}
x2x_{2}
x_{3}
x3x_{3}
\bold{ z^{(2)}}
z(2)\bold{ z^{(2)}}
\bold{ a^{(2)}}
a(2)\bold{ a^{(2)}}
\bold{ z^{(3)}}
z(3)\bold{ z^{(3)}}
\bold{ a^{(1)} }
a(1)\bold{ a^{(1)} }
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
W^{(1)}
W(1)W^{(1)}
W^{(2)}
W(2)W^{(2)}
W^{(3)}
W(3)W^{(3)}
\bold{ z^{(4)}}
z(4)\bold{ z^{(4)}}
\bold{ a^{(3)}}
a(3)\bold{ a^{(3)}}
\color{Green}{ \bold{ z^{(4)} }} = \bold{ W^{(3)}. \color{red}{a^{(3)}} }
z(4)=W(3).a(3)\color{Green}{ \bold{ z^{(4)} }} = \bold{ W^{(3)}. \color{red}{a^{(3)}} }
\color{Green}{z^{(4)}_{i}} =\sum_{j} W^{(3)}_{ij}. \color{Red}{a^{(3)}_{j}}
zi(4)=∑jWij(3).aj(3)\color{Green}{z^{(4)}_{i}} =\sum_{j} W^{(3)}_{ij}. \color{Red}{a^{(3)}_{j}}
\bold{x} =
x=\bold{x} =
x_{1}
x1x_{1}
x_{2}
x2x_{2}
x_{3}
x3x_{3}
\bold{ z^{(2)}}
z(2)\bold{ z^{(2)}}
\bold{ a^{(2)}}
a(2)\bold{ a^{(2)}}
\bold{ z^{(3)}}
z(3)\bold{ z^{(3)}}
\bold{ a^{(1)} }
a(1)\bold{ a^{(1)} }
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
W^{(1)}
W(1)W^{(1)}
W^{(2)}
W(2)W^{(2)}
\color{Red}{ \bold{ a^{(4)} }} = g( \bold{ \color{Green}{z^{(4)}} } )
a(4)=g(z(4))\color{Red}{ \bold{ a^{(4)} }} = g( \bold{ \color{Green}{z^{(4)}} } )
\color{Red}{a^{(4)}_{j}} =g( \color{Green}{z^{(4)}_{i}} )
aj(4)=g(zi(4))\color{Red}{a^{(4)}_{j}} =g( \color{Green}{z^{(4)}_{i}} )
W^{(3)}
W(3)W^{(3)}
\bold{ z^{(4)}}
z(4)\bold{ z^{(4)}}
\bold{ a^{(4)}}
a(4)\bold{ a^{(4)}}
\bold{ a^{(3)}}
a(3)\bold{ a^{(3)}}
\bold{x} =
x=\bold{x} =
x_{1}
x1x_{1}
x_{2}
x2x_{2}
x_{3}
x3x_{3}
\bold{ z^{(2)}}
z(2)\bold{ z^{(2)}}
\bold{ a^{(2)}}
a(2)\bold{ a^{(2)}}
\bold{ z^{(3)}}
z(3)\bold{ z^{(3)}}
\bold{ a^{(1)} }
a(1)\bold{ a^{(1)} }
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
W^{(1)}
W(1)W^{(1)}
W^{(2)}
W(2)W^{(2)}
\bold{ \hat{y} }
y^\bold{ \hat{y} }
\hat{y}_{1}
y^1\hat{y}_{1}
\hat{y}_{2}
y^2\hat{y}_{2}
\hat{y}_{3 }
y^3\hat{y}_{3 }
\hat{y}_{c} = \frac{\exp(a_{c}^{(4)})}{\sum_{j}\exp(a_{j}^{(4)})}
y^c=exp(ac(4))∑jexp(aj(4))\hat{y}_{c} = \frac{\exp(a_{c}^{(4)})}{\sum_{j}\exp(a_{j}^{(4)})}
W^{(3)}
W(3)W^{(3)}
\bold{ z^{(4)}}
z(4)\bold{ z^{(4)}}
\bold{ a^{(4)}}
a(4)\bold{ a^{(4)}}
\bold{ a^{(3)}}
a(3)\bold{ a^{(3)}}

Softmax function

\hat{y}_{c}
y^c\hat{y}_{c}

probability of the sample

to belong to class c

Loss function

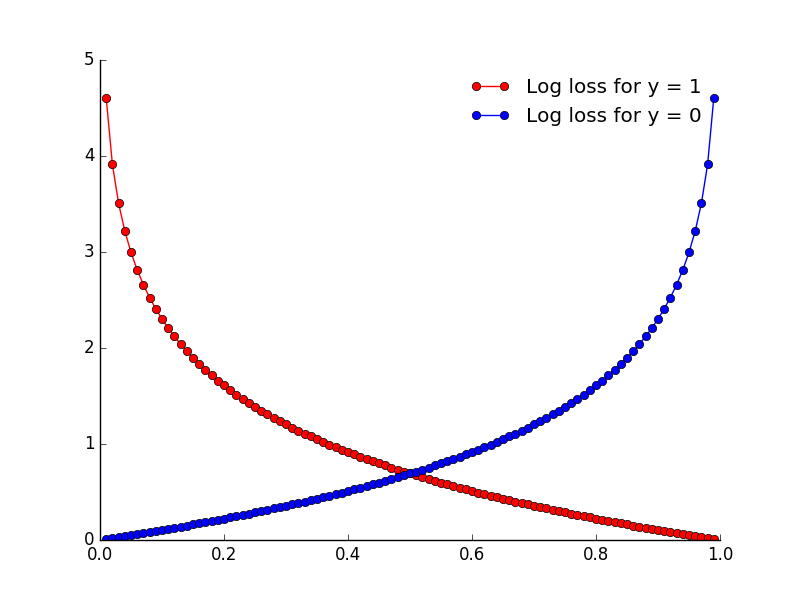
\left \{ (\bold{x^{(1)}},\bold{y^{(1)}}),(\bold{x^{(2)}},\bold{y^{(2)}}),...,(\bold{x^{(m)}},\bold{y^{(m)}}) \right \}
{(x(1),y(1)),(x(2),y(2)),...,(x(m),y(m))}\left \{ (\bold{x^{(1)}},\bold{y^{(1)}}),(\bold{x^{(2)}},\bold{y^{(2)}}),...,(\bold{x^{(m)}},\bold{y^{(m)}}) \right \}

Gradient descent

Gradient descent

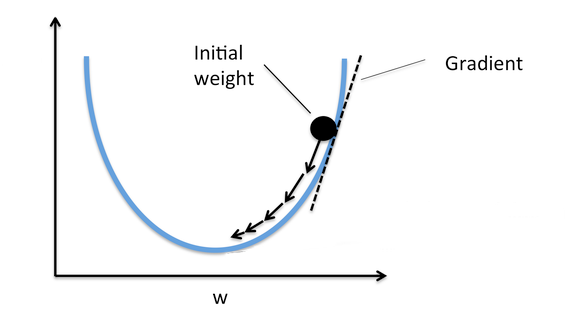
  • A vector
  • The direction of quickest increase

Backward propagation

How to compute

\bold{x} =
x=\bold{x} =
x_{1}
x1x_{1}
x_{2}
x2x_{2}
x_{3}
x3x_{3}
\bold{ z^{(2)}}
z(2)\bold{ z^{(2)}}
\bold{ a^{(2)}}
a(2)\bold{ a^{(2)}}
\bold{ z^{(3)}}
z(3)\bold{ z^{(3)}}
\bold{ a^{(1)} }
a(1)\bold{ a^{(1)} }
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
W^{(1)}
W(1)W^{(1)}
W^{(2)}
W(2)W^{(2)}
\bold{ \hat{y} }
y^\bold{ \hat{y} }
\hat{y}_{1}
y^1\hat{y}_{1}
\hat{y}_{2}
y^2\hat{y}_{2}
\hat{y}_{3 }
y^3\hat{y}_{3 }
W^{(3)}
W(3)W^{(3)}
\bold{ z^{(4)}}
z(4)\bold{ z^{(4)}}
\bold{ a^{(4)}}
a(4)\bold{ a^{(4)}}
\bold{ a^{(3)}}
a(3)\bold{ a^{(3)}}
W^{(3)}_{11}
W11(3)W^{(3)}_{11}

}

\bold{x} =
x=\bold{x} =
x_{1}
x1x_{1}
x_{2}
x2x_{2}
x_{3}
x3x_{3}
\bold{ z^{(2)}}
z(2)\bold{ z^{(2)}}
\bold{ a^{(2)}}
a(2)\bold{ a^{(2)}}
\bold{ z^{(3)}}
z(3)\bold{ z^{(3)}}
\bold{ a^{(1)} }
a(1)\bold{ a^{(1)} }
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
W^{(1)}
W(1)W^{(1)}
W^{(2)}
W(2)W^{(2)}
\bold{ \hat{y} }
y^\bold{ \hat{y} }
\hat{y}_{1}
y^1\hat{y}_{1}
\hat{y}_{2}
y^2\hat{y}_{2}
\hat{y}_{3 }
y^3\hat{y}_{3 }
W^{(3)}
W(3)W^{(3)}
\bold{ z^{(4)}}
z(4)\bold{ z^{(4)}}
\bold{ a^{(4)}}
a(4)\bold{ a^{(4)}}
\bold{ a^{(3)}}
a(3)\bold{ a^{(3)}}
W^{(3)}_{11}
W11(3)W^{(3)}_{11}

}

\bold{x} =
x=\bold{x} =
x_{1}
x1x_{1}
x_{2}
x2x_{2}
x_{3}
x3x_{3}
\bold{ z^{(2)}}
z(2)\bold{ z^{(2)}}
\bold{ a^{(2)}}
a(2)\bold{ a^{(2)}}
\bold{ z^{(3)}}
z(3)\bold{ z^{(3)}}
\bold{ a^{(1)} }
a(1)\bold{ a^{(1)} }
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
W^{(1)}
W(1)W^{(1)}
W^{(2)}
W(2)W^{(2)}
\bold{ \hat{y} }
y^\bold{ \hat{y} }
\hat{y}_{1}
y^1\hat{y}_{1}
\hat{y}_{2}
y^2\hat{y}_{2}
\hat{y}_{3 }
y^3\hat{y}_{3 }
W^{(3)}
W(3)W^{(3)}
\bold{ z^{(4)}}
z(4)\bold{ z^{(4)}}
\bold{ a^{(4)}}
a(4)\bold{ a^{(4)}}
\bold{ a^{(3)}}
a(3)\bold{ a^{(3)}}

}

\bold{x} =
x=\bold{x} =
x_{1}
x1x_{1}
x_{2}
x2x_{2}
x_{3}
x3x_{3}
\bold{ z^{(2)}}
z(2)\bold{ z^{(2)}}
\bold{ a^{(2)}}
a(2)\bold{ a^{(2)}}
\bold{ z^{(3)}}
z(3)\bold{ z^{(3)}}
\bold{ a^{(1)} }
a(1)\bold{ a^{(1)} }
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
g()
g()g()
W^{(1)}
W(1)W^{(1)}
W^{(2)}
W(2)W^{(2)}
\bold{ \hat{y} }
y^\bold{ \hat{y} }
\hat{y}_{1}
y^1\hat{y}_{1}
\hat{y}_{2}
y^2\hat{y}_{2}
\hat{y}_{3 }
y^3\hat{y}_{3 }
W^{(3)}
W(3)W^{(3)}
\bold{ z^{(4)}}
z(4)\bold{ z^{(4)}}
\bold{ a^{(4)}}
a(4)\bold{ a^{(4)}}
\bold{ a^{(3)}}
a(3)\bold{ a^{(3)}}

}

Neural Networks - Backward propagation

By Tiphaine Champetier

Made with Slides.com

Neural Networks - Backward propagation

  • 614

More from Tiphaine Champetier