A multiscale neural network


Tiphaine Champetier - Team biocomp
21st March 2017
Neural Network
What for?
Classification


Features vector
Class / Label / Category



Perceptron
Linear combination of
inputs

Neural Network
Compute a more complex
function

Foward propagation
\bold{x}
x
x_{1}
x1
x_{2}
x2
x_{3}
x3
\bold{x}
=
x=
x_{1}
x1
x_{2}
x2
x_{3}
x3



\bold{
a^{(1)}
}
a(1)
\bold{x}
=
x=
x_{1}
x1
x_{2}
x2
x_{3}
x3



\bold{
a^{(1)}
}
a(1)
W^{(1)}
W(1)
\bold{x}
=
x=
x_{1}
x1
x_{2}
x2
x_{3}
x3
\bold{
z^{(2)}}
z(2)







\bold{
a^{(1)}
}
a(1)
W^{(1)}
W(1)
\color{Green}{
\bold{
z^{(2)}
}}
=
\bold{
W^{(1)}.
\color{red}{a^{(1)}}
}
z(2)=W(1).a(1)
\color{Green}{z^{(2)}_{i}}
=\sum_{j}
W^{(1)}_{ij}.
\color{Red}{a^{(1)}_{j}}
zi(2)=∑jWij(1).aj(1)
\bold{x}
=
x=
x_{1}
x1
x_{2}
x2
x_{3}
x3
\bold{
z^{(2)}}
z(2)








\bold{
a^{(2)}}
a(2)



\bold{
a^{(1)}
}
a(1)
g()
g()
g()
g()
g()
g()
g()
g()
W^{(1)}
W(1)
\color{Red}{
\bold{
a^{(2)}
}}
=
g(
\bold{
\color{Green}{z^{(2)}}
}
)
a(2)=g(z(2))
\color{Red}{a^{(2)}_{j}}
=g(
\color{Green}{z^{(2)}_{i}}
)
aj(2)=g(zi(2))
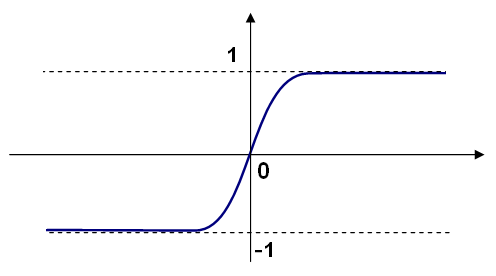
\bold{x}
=
x=
x_{1}
x1
x_{2}
x2
x_{3}
x3
\bold{
z^{(2)}}
z(2)








\bold{
a^{(2)}}
a(2)




\bold{
z^{(3)}}
z(3)



\bold{
a^{(1)}
}
a(1)
g()
g()
g()
g()
g()
g()
g()
g()
W^{(1)}
W(1)
W^{(2)}
W(2)
\color{Green}{
\bold{
z^{(3)}
}}
=
\bold{
W^{(2)}.
\color{red}{a^{(2)}}
}
z(3)=W(2).a(2)
\color{Green}{z^{(3)}_{i}}
=\sum_{j}
W^{(2)}_{ij}.
\color{Red}{a^{(2)}_{j}}
zi(3)=∑jWij(2).aj(2)
\bold{x}
=
x=
x_{1}
x1
x_{2}
x2
x_{3}
x3
\bold{
z^{(2)}}
z(2)








\bold{
a^{(2)}}
a(2)




\bold{
z^{(3)}}
z(3)



\bold{
a^{(1)}
}
a(1)
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
W^{(1)}
W(1)
W^{(2)}
W(2)




\bold{
a^{(3)}}
a(3)
\color{Red}{
\bold{
a^{(3)}
}}
=
g(
\bold{
\color{Green}{z^{(3)}}
}
)
a(3)=g(z(3))
\color{Red}{a^{(3)}_{j}}
=g(
\color{Green}{z^{(3)}_{i}}
)
aj(3)=g(zi(3))
\bold{x}
=
x=
x_{1}
x1
x_{2}
x2
x_{3}
x3
\bold{
z^{(2)}}
z(2)








\bold{
a^{(2)}}
a(2)




\bold{
z^{(3)}}
z(3)



\bold{
a^{(1)}
}
a(1)
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
W^{(1)}
W(1)
W^{(2)}
W(2)







W^{(3)}
W(3)
\bold{
z^{(4)}}
z(4)
\bold{
a^{(3)}}
a(3)
\color{Green}{
\bold{
z^{(4)}
}}
=
\bold{
W^{(3)}.
\color{red}{a^{(3)}}
}
z(4)=W(3).a(3)
\color{Green}{z^{(4)}_{i}}
=\sum_{j}
W^{(3)}_{ij}.
\color{Red}{a^{(3)}_{j}}
zi(4)=∑jWij(3).aj(3)
\bold{x}
=
x=
x_{1}
x1
x_{2}
x2
x_{3}
x3
\bold{
z^{(2)}}
z(2)








\bold{
a^{(2)}}
a(2)




\bold{
z^{(3)}}
z(3)



\bold{
a^{(1)}
}
a(1)
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
W^{(1)}
W(1)
W^{(2)}
W(2)
\color{Red}{
\bold{
a^{(4)}
}}
=
g(
\bold{
\color{Green}{z^{(4)}}
}
)
a(4)=g(z(4))
\color{Red}{a^{(4)}_{j}}
=g(
\color{Green}{z^{(4)}_{i}}
)
aj(4)=g(zi(4))










W^{(3)}
W(3)
\bold{
z^{(4)}}
z(4)
\bold{
a^{(4)}}
a(4)
\bold{
a^{(3)}}
a(3)
\bold{x}
=
x=
x_{1}
x1
x_{2}
x2
x_{3}
x3
\bold{
z^{(2)}}
z(2)








\bold{
a^{(2)}}
a(2)




\bold{
z^{(3)}}
z(3)



\bold{
a^{(1)}
}
a(1)
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
g()
W^{(1)}
W(1)
W^{(2)}
W(2)
\bold{
\hat{y}
}
y^
\hat{y}_{1}
y^1
\hat{y}_{2}
y^2
\hat{y}_{3
}
y^3
\hat{y}_{c}
=
\frac{\exp(a_{c}^{(4)})}{\sum_{j}\exp(a_{j}^{(4)})}
y^c=∑jexp(aj(4))exp(ac(4))










W^{(3)}
W(3)
\bold{
z^{(4)}}
z(4)
\bold{
a^{(4)}}
a(4)
\bold{
a^{(3)}}
a(3)
Softmax function
\hat{y}_{c}
y^c
probability of the sample
to belong to class c
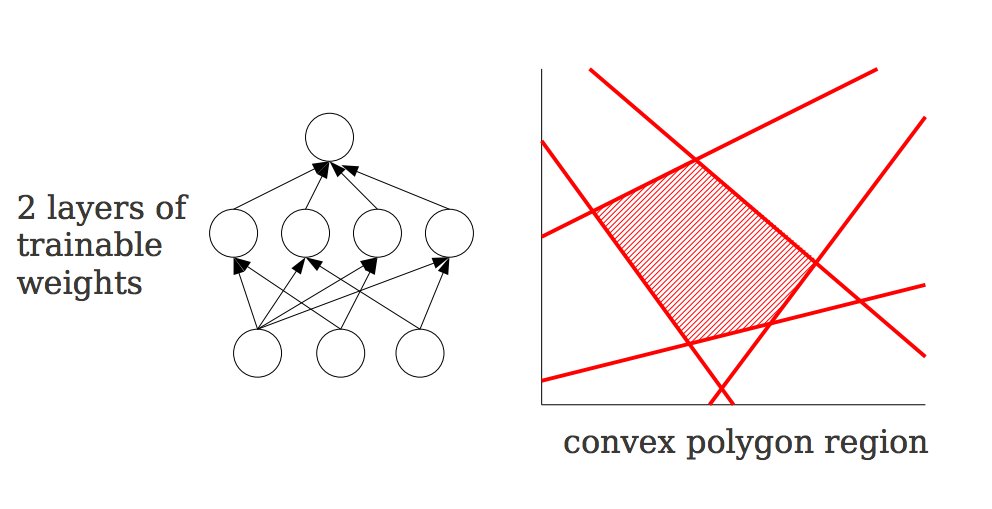
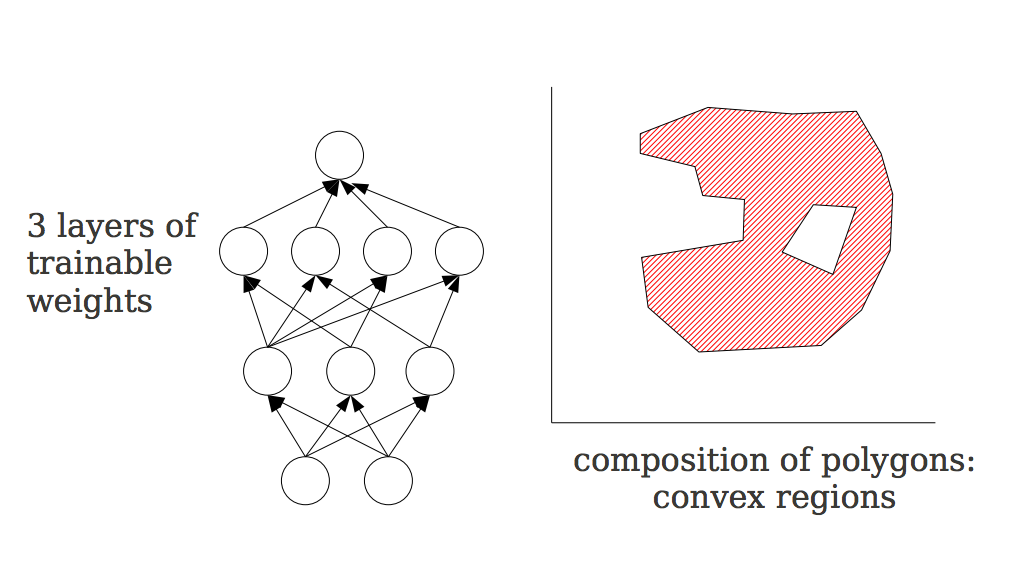
Convolutional neural network
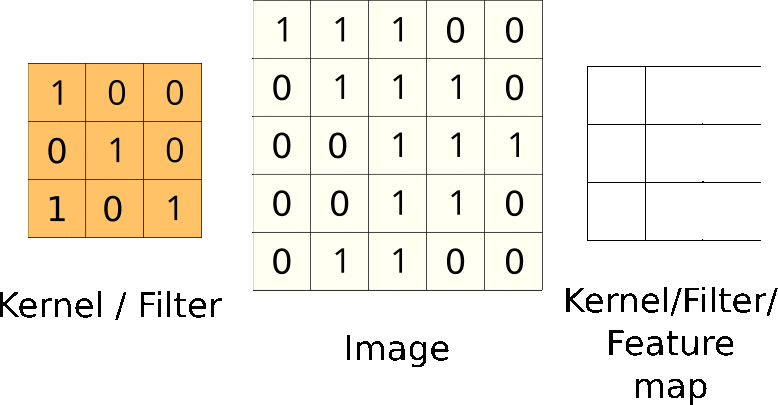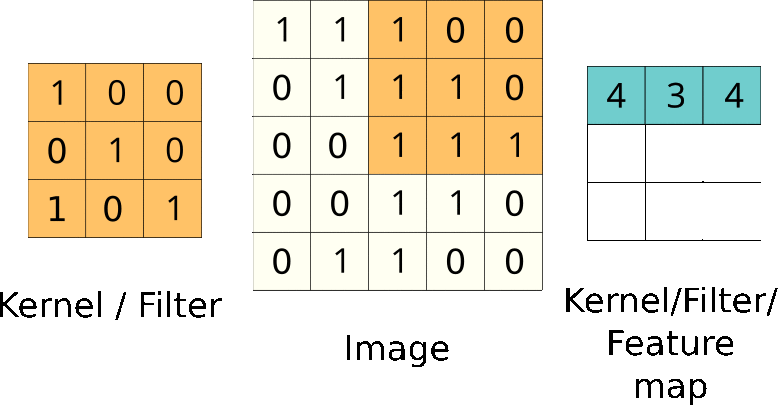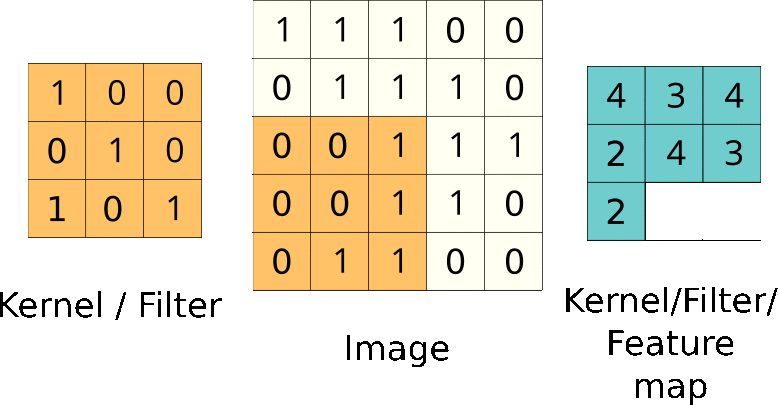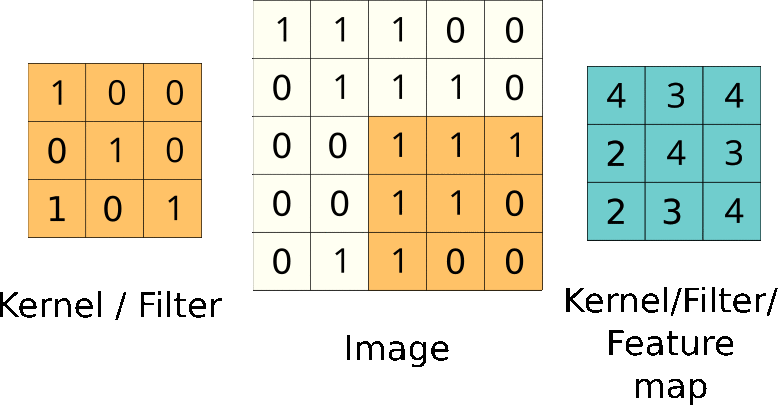
Convolution



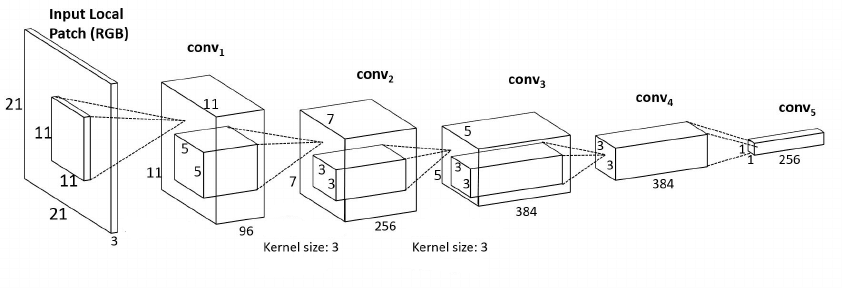
Architecture of the feature extractor
Filter combining
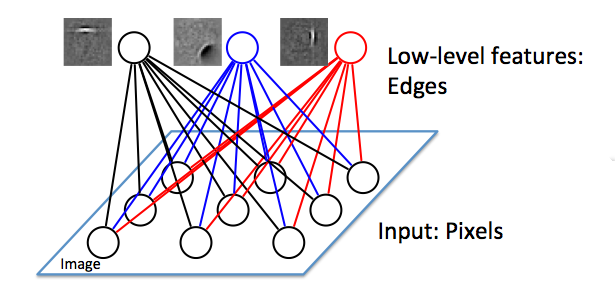
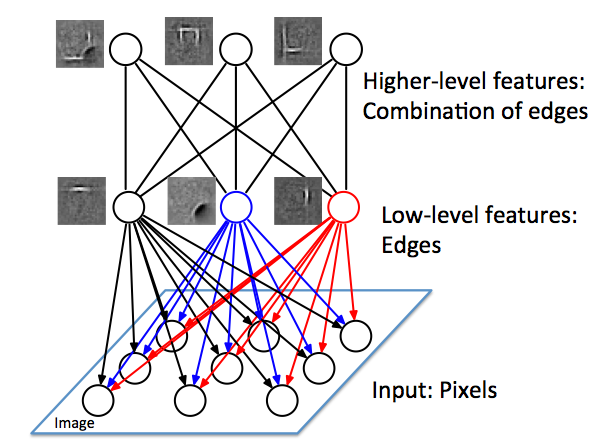
Filter combining
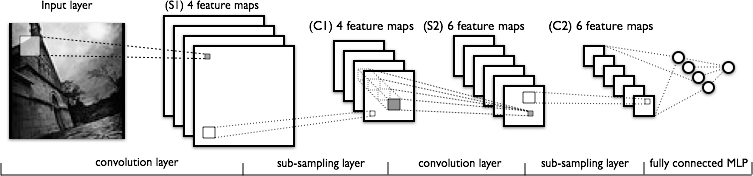
Global architecture
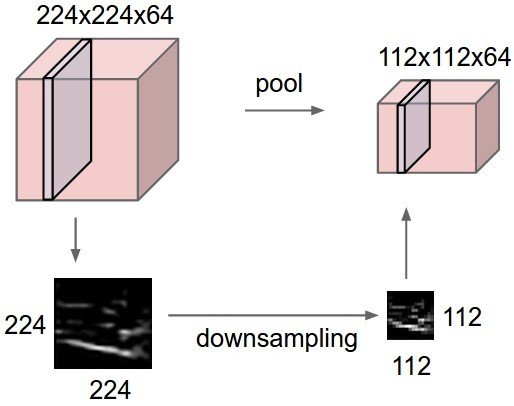
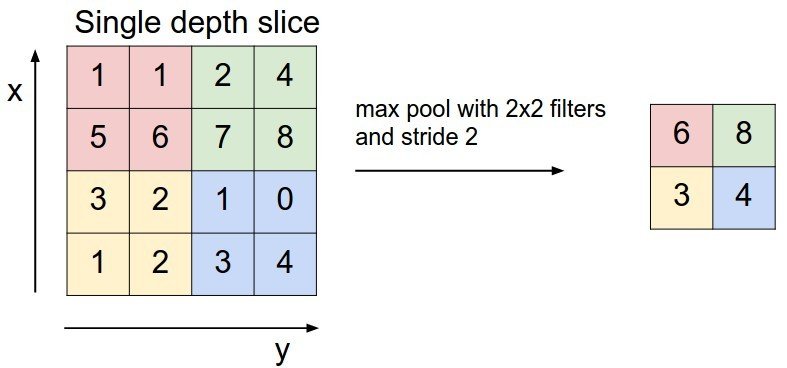
Pooling / Sub-sampling

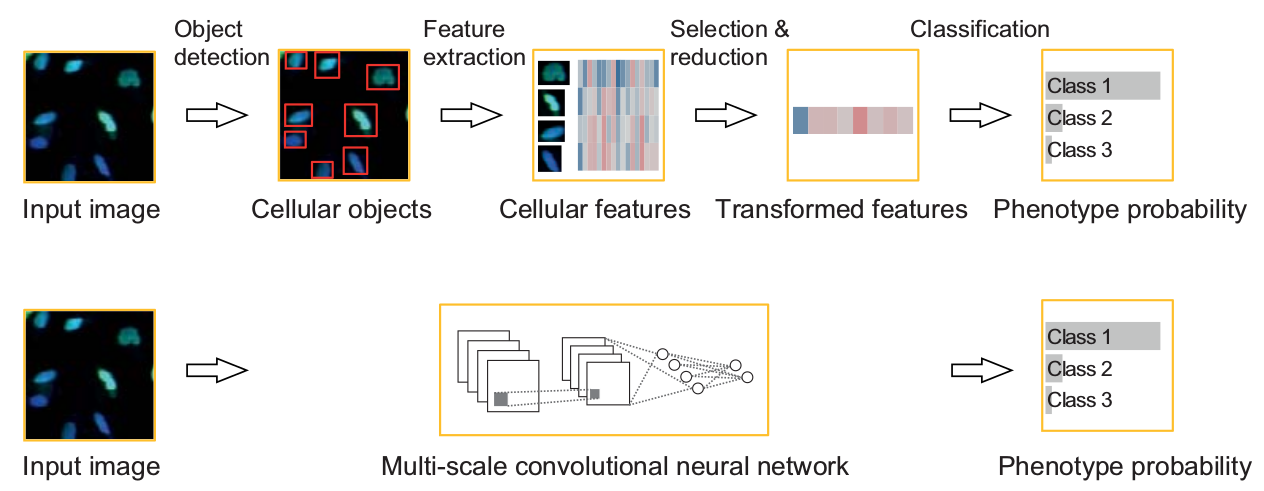
Why a neural network for image analysis ?
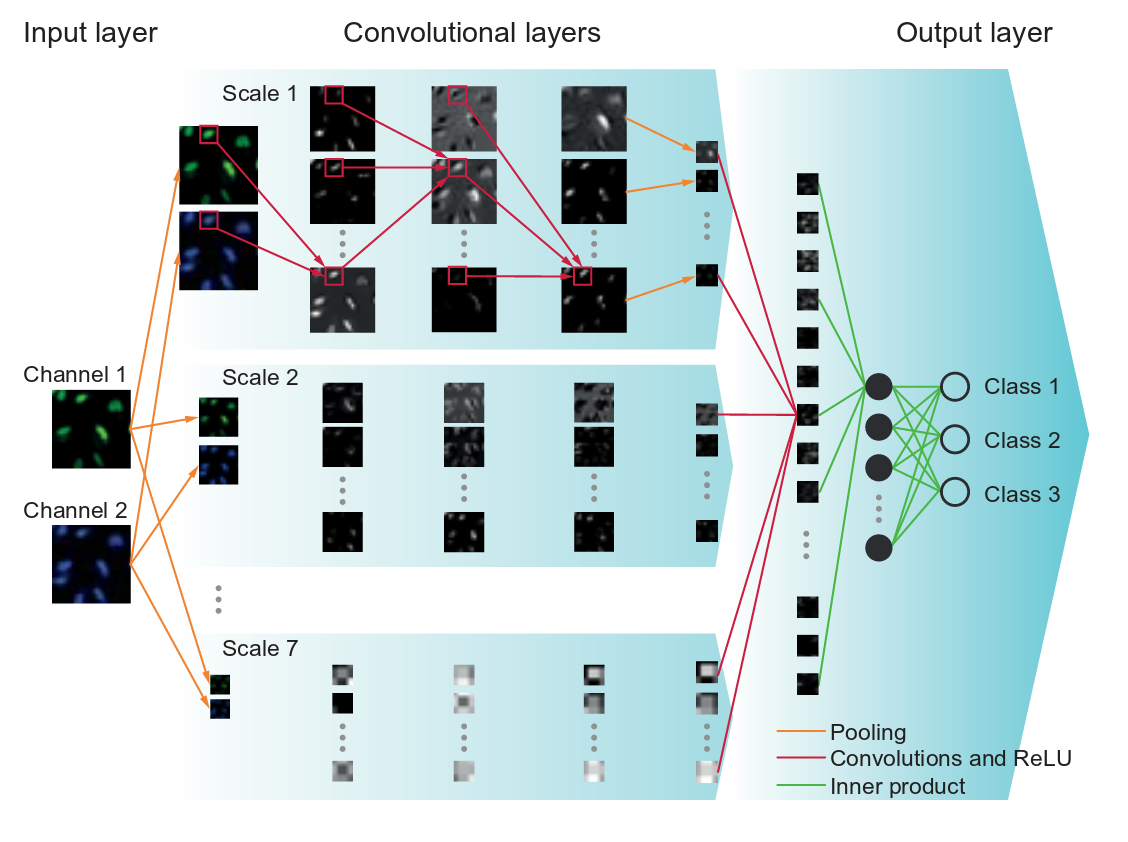
The mustiscale neural network
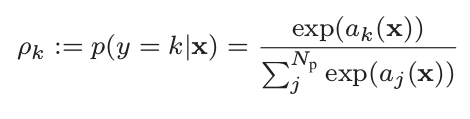
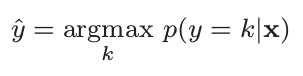
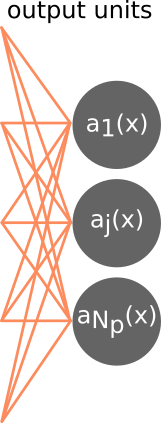
Softmax function
Classification accuracies
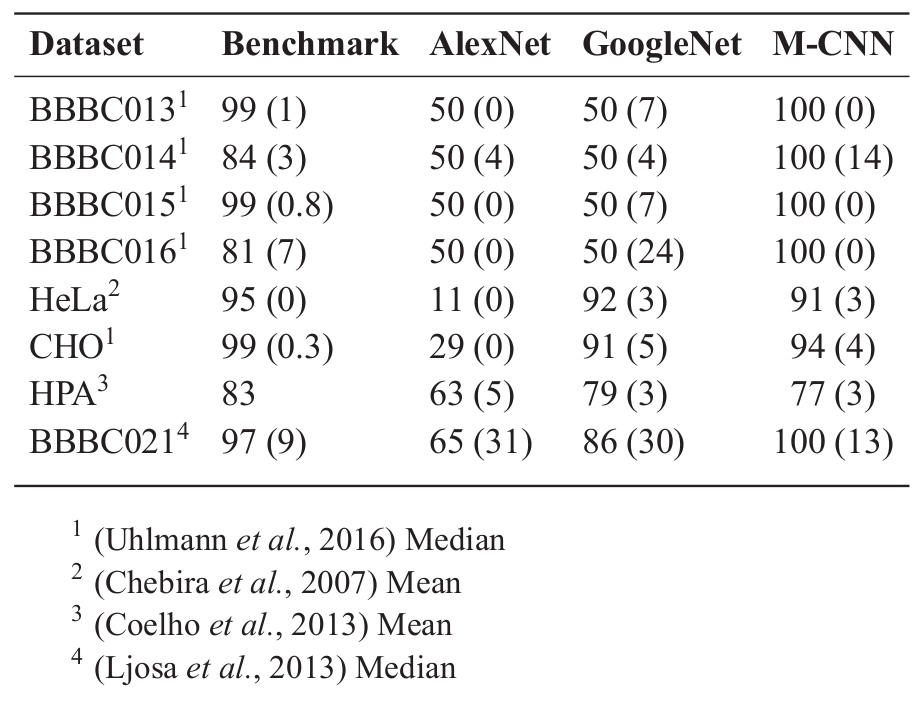
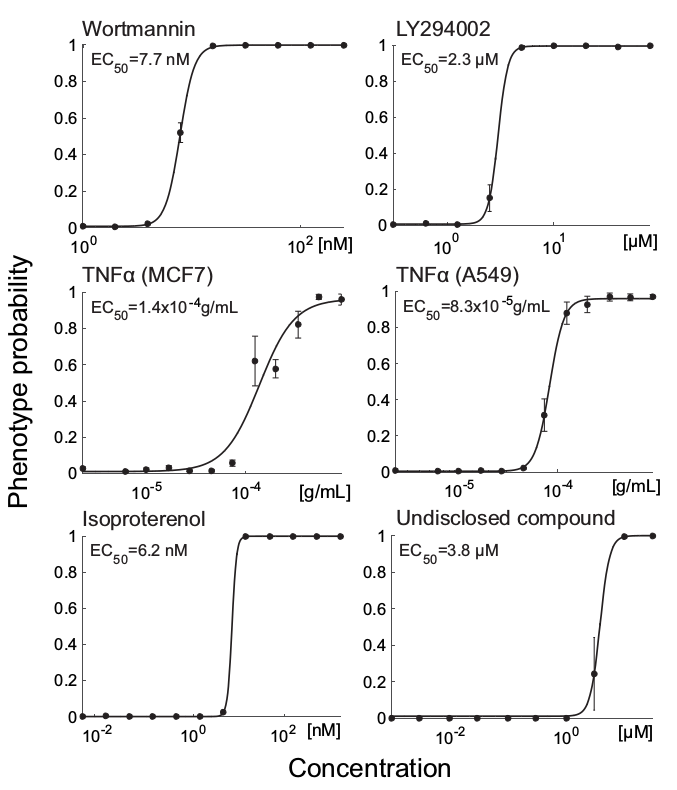
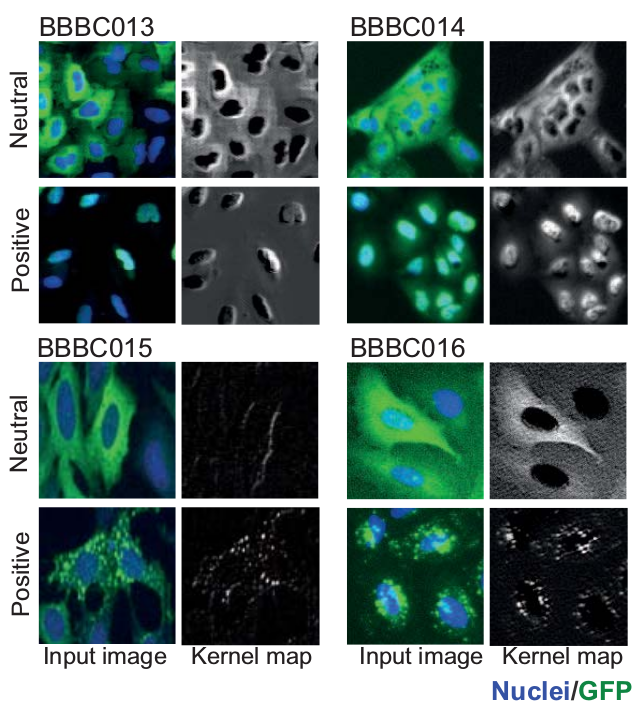
Binary phenotype classification
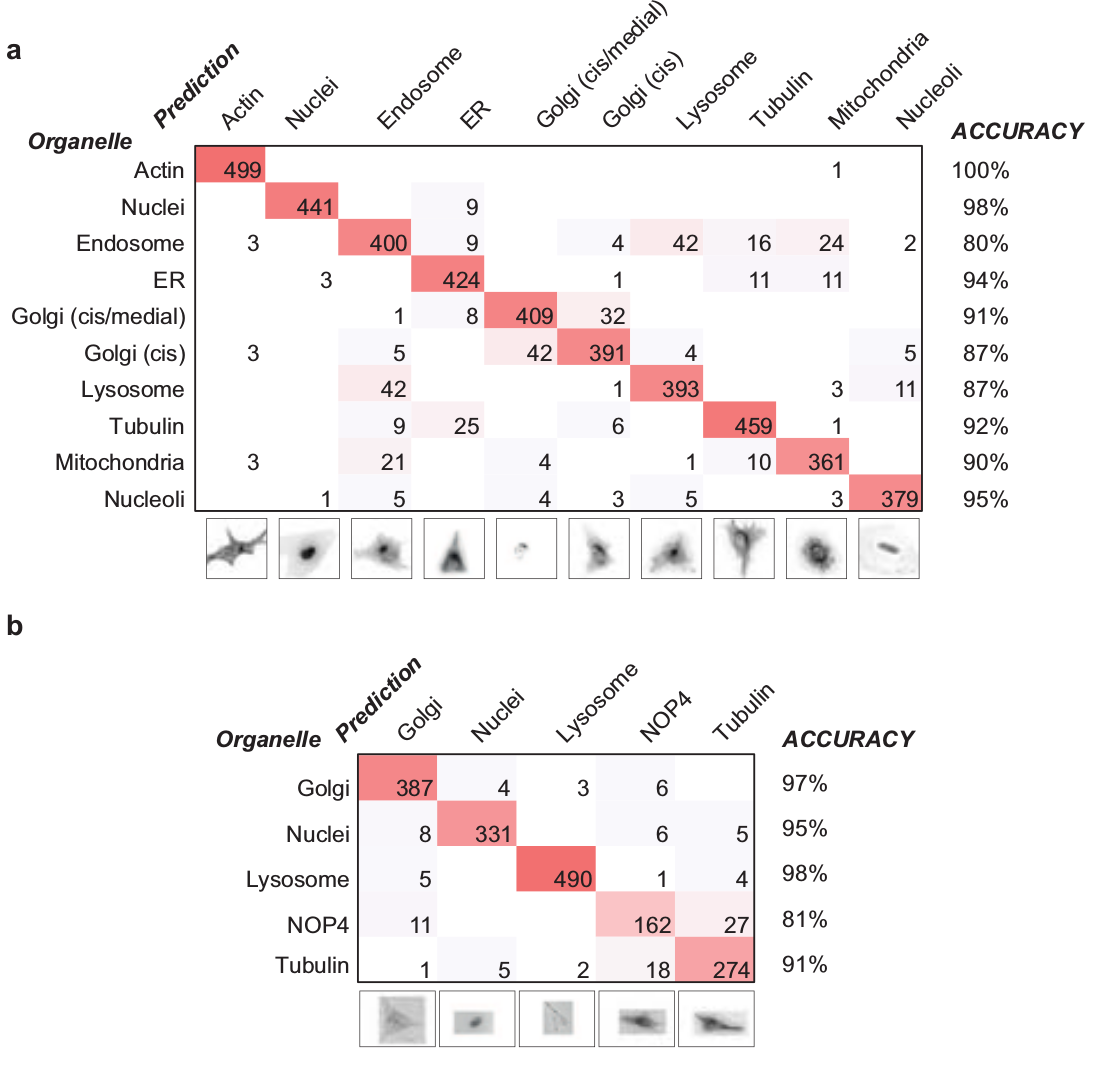
Multi-label classification of organelles
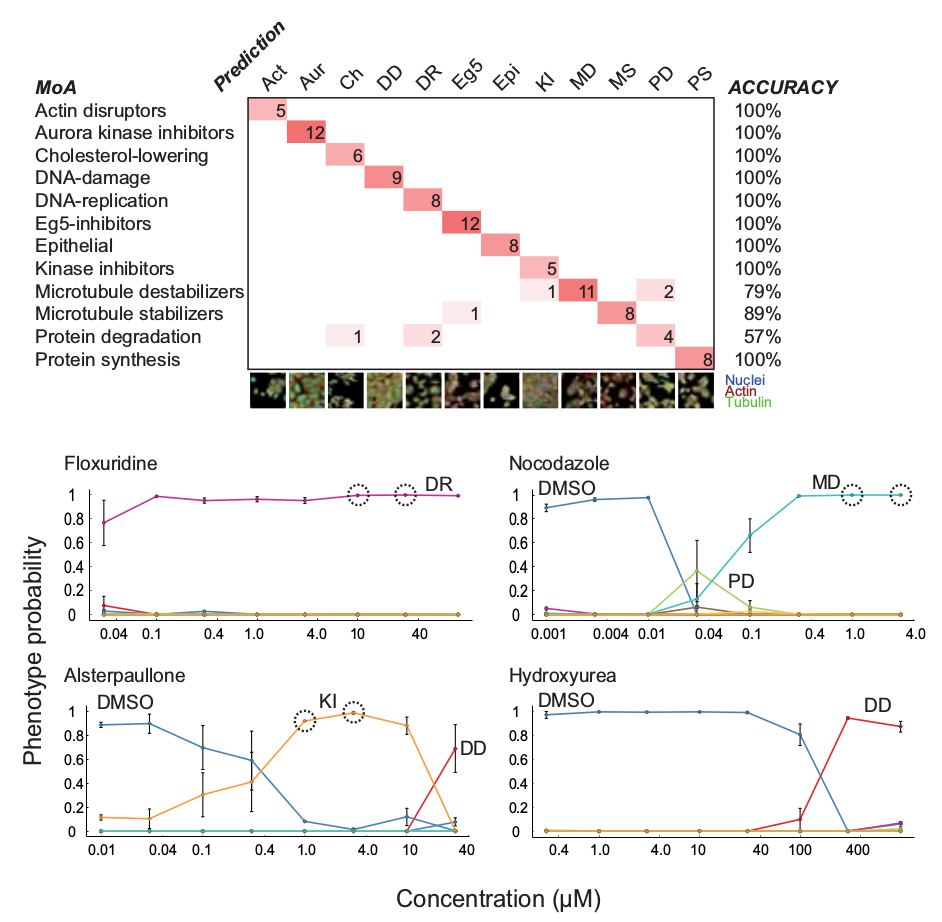
Multi-label Classification and prediction of MoA
Thank you !
deck
By Tiphaine Champetier
deck
- 323


